Radio de la Tierra

Radio de la Tierra
Radios terrestres ecuatoriales ( a ), polares ( b ) y medios aritméticos según se definen en la revisión del Sistema Geodésico Mundial de 1984 (no a escala)
Otros nombres	radio terrestre
Símbolos comunes	R 🜨 , R E , a , b , a E , b E , R e E , R p E
Unidad SI	metros
En unidades base del SI	metro
Comportamiento bajo transformación de coordenadas	escalar
Dimensión	${\displaystyle {\mathsf {L}}}$
Valor	Radio ecuatorial : a = (6 378 .1370 km ) Radio polar : b = (6 356,7523 kilómetros )

Radio nominal de la Tierra
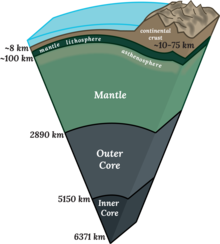Sección transversal del interior de la Tierra
información general
Sistema de unidades	astronomía , geofísica
Unidad de	distancia
Símbolo	${\displaystyle {\mathcal {R}}_{\mathrm {E} }^{\mathrm {N} }}$,  ,${\displaystyle {\mathcal {R}}_{e\mathrm {E} }^{\mathrm {N} }}$${\displaystyle {\mathcal {R}}_{p\mathrm {E} }^{\mathrm {N} }}$
Conversiones
1  en...${\displaystyle {\mathcal {R}}_{\mathrm {E} }^{\mathrm {N} }}$	... es igual a...
Unidad base del SI	6,3781 × 10 6  m [1]
Sistema métrico	6.357 a 6.378 kilómetros
Unidades inglesas	3.950 a 3.963 millas

Geodesia
Fundamentos Geodesia Geodinámica Geomática Historia
Conceptos Distancia geográfica Geoide Figura de la Tierra (radio y circunferencia ) Coordenadas geodésicas Datum geodésico Geodésico Representación de la posición horizontal Latitud  / Longitud Proyección de mapas Elipsoide de referencia Geodesia satelital Sistema de referencia espacial Relaciones espaciales Posiciones verticales
Tecnologías Sistemas globales de navegación por satélite (GNSS) Sistema de Posición Global (GPS) GLONASS (Rusia) BeiDou (BDS) (China) Galileo (Europa) NAVIC (India) Sistema satelital cuasi-cenital (QZSS) (Japón) Cuadrícula global discreta y geocodificación
Normas (historia) Valor nominal del vehículo 29 Datum del nivel del mar 1929 OSGB36 Ordnance Survey de Gran Bretaña, 1936 SK-42 Sistema Coordinat 1942 goda ED50 Fecha europea 1950 Triste69 Datum sudamericano 1969 80 gr Sistema de referencia geodésica 1980 ISO 6709 Punto geográfico coord. 1983 NAD83 Datum norteamericano 1983 WGS84 Sistema Geodésico Mundial 1984 Navegación 88 Datum vertical norteamericano 1988 ETRS89 Sistema de referencia terrestre europeo 1989 GCJ-02 Datos chinos confusos de 2002 URI geográfica Enlace de Internet a un punto 2010 Sistema Internacional de Referencia Terrestre Identificador del sistema de referencia espacial (SRID) Medida universal transversal de Mercator (UTM)
en a mi

El radio de la Tierra (denotado como R _🜨 o R _E ) es la distancia desde el centro de la Tierra hasta un punto en o cerca de su superficie. Aproximando la figura de la Tierra por un esferoide terrestre (un elipsoide achatado ), el radio varía desde un máximo ( radio ecuatorial , denotado como a ) de casi 6.378 km (3.963 mi) a un mínimo ( radio polar , denotado como b ) de casi 6.357 km (3.950 mi).

Un valor promedio global se considera generalmente 6,371 kilómetros (3,959 mi) con una variabilidad del 0.3% (±10 km) por las siguientes razones. La Unión Internacional de Geodesia y Geofísica (IUGG) proporciona tres valores de referencia: el radio medio ( R ₁ ) de tres radios medidos en dos puntos del ecuador y un polo; el radio autálico , que es el radio de una esfera con la misma área de superficie ( R ₂ ); y el radio volumétrico , que es el radio de una esfera que tiene el mismo volumen que el elipsoide ( R ₃ ). ^[2] Los tres valores son aproximadamente 6,371 kilómetros (3,959 mi).

Otras formas de definir y medir el radio de la Tierra implican el radio de curvatura del esferoide o la topografía real . Algunas definiciones arrojan valores fuera del rango entre el radio polar y el radio ecuatorial porque tienen en cuenta efectos localizados.

En astronomía y geofísica a veces se utiliza un radio nominal de la Tierra (denominado ) como unidad de medida , un factor de conversión utilizado al expresar propiedades planetarias como múltiplos o fracciones de un radio terrestre constante; si la elección entre radios ecuatoriales o polares no es explícita, se debe asumir el radio ecuatorial, como lo recomienda la Unión Astronómica Internacional (UAI). ^[1]${\displaystyle {\mathcal {R}}_{\mathrm {E} }^{\mathrm {N} }}$

La rotación de la Tierra , las variaciones de densidad interna y las fuerzas de marea externas hacen que su forma se desvíe sistemáticamente de una esfera perfecta. ^[a] La topografía local aumenta la variabilidad, lo que da como resultado una superficie de profunda complejidad. Nuestras descripciones de la superficie de la Tierra deben ser más simples que la realidad para ser manejables. Por lo tanto, creamos modelos para aproximarnos a las características de la superficie de la Tierra, generalmente basándonos en el modelo más simple que se adapte a la necesidad.

Cada uno de los modelos de uso común implica alguna noción de radio geométrico . Estrictamente hablando, las esferas son los únicos sólidos que tienen radios, pero los usos más amplios del término radio son comunes en muchos campos, incluidos aquellos que tratan con modelos de la Tierra. La siguiente es una lista parcial de modelos de la superficie de la Tierra, ordenados desde el más exacto hasta el más aproximado:

• La superficie real de la Tierra
• El geoide , definido por el nivel medio del mar en cada punto de la superficie real ^[b]
• Un esferoide , también llamado elipsoide de revolución, geocéntrico para modelar toda la Tierra, o bien geodésico para trabajos regionales ^[c]
• Una esfera

En el caso del geoide y los elipsoides, la distancia fija desde cualquier punto del modelo hasta el centro especificado se denomina "radio de la Tierra" o "radio de la Tierra en ese punto" . ^[d] También es común referirse a cualquier radio medio de un modelo esférico como "radio de la Tierra" . Por otro lado, al considerar la superficie real de la Tierra, es poco común referirse a un "radio", ya que generalmente no hay una necesidad práctica. Más bien, es útil la elevación sobre o debajo del nivel del mar.

Independientemente del modelo, cualquiera de estos radios geocéntricos se encuentra entre el mínimo polar de unos 6.357 km y el máximo ecuatorial de unos 6.378 km (3.950 a 3.963 mi). Por lo tanto, la Tierra se desvía de una esfera perfecta en solo un tercio de un porcentaje, lo que respalda el modelo esférico en la mayoría de los contextos y justifica el término "radio de la Tierra". Si bien los valores específicos difieren, los conceptos de este artículo se generalizan a cualquier planeta principal .

La rotación de un planeta hace que se aproxime a un elipsoide /esferoide achatado con una protuberancia en el ecuador y un achatamiento en los polos norte y sur , de modo que el radio ecuatorial a es mayor que el radio polar b en aproximadamente aq . La constante de achatamiento q está dada por

${\displaystyle q={\frac {a^{3}\omega ^{2}}{GM}}\,,}$

donde ω es la frecuencia angular , G es la constante gravitacional y M es la masa del planeta. ^[e] Para la Tierra ⁠1/q⁠ ≈ 289 , que está cerca del aplanamiento inverso medido1/F⁠ ≈ 298.257 . Además, el abultamiento en el ecuador muestra variaciones lentas. El abultamiento había estado disminuyendo, pero desde 1998 ha aumentado, posiblemente debido a la redistribución de la masa oceánica a través de las corrientes. ^[4]

La variación en la densidad y el espesor de la corteza hace que la gravedad varíe a lo largo de la superficie y en el tiempo, de modo que el nivel medio del mar difiere del elipsoide. Esta diferencia es la altura del geoide , positiva por encima o fuera del elipsoide, negativa por debajo o dentro. La variación de la altura del geoide es inferior a 110 m (360 pies) en la Tierra. La altura del geoide puede cambiar abruptamente debido a terremotos (como el terremoto de Sumatra-Andamán ) o la reducción de las masas de hielo (como en Groenlandia ). ^[5]

No todas las deformaciones se originan en el interior de la Tierra. La atracción gravitatoria de la Luna o del Sol puede hacer que la superficie de la Tierra en un punto determinado varíe en décimas de metro a lo largo de un período de casi 12 horas (véase marea terrestre ).

Dadas las influencias locales y transitorias sobre la altura de la superficie, los valores definidos a continuación se basan en un modelo de "propósito general", refinado de la manera más precisa posible a nivel global dentro de los 5 m (16 pies) de la altura del elipsoide de referencia y dentro de los 100 m (330 pies) del nivel medio del mar (sin tener en cuenta la altura del geoide).

Además, el radio se puede estimar a partir de la curvatura de la Tierra en un punto. Al igual que un toro , la curvatura en un punto será mayor (más cerrada) en una dirección (norte-sur en la Tierra) y menor (más plana) perpendicularmente (este-oeste). El radio de curvatura correspondiente depende de la ubicación y la dirección de la medición desde ese punto. Una consecuencia es que la distancia al horizonte verdadero en el ecuador es ligeramente más corta en la dirección norte-sur que en la dirección este-oeste.

En resumen, las variaciones locales del terreno impiden definir un único radio "preciso". Solo se puede adoptar un modelo idealizado. Desde la estimación de Eratóstenes , se han creado muchos modelos. Históricamente, estos modelos se basaban en la topografía regional, lo que proporcionaba el mejor elipsoide de referencia ^{[ ancla rota ]} para el área estudiada. A medida que la teledetección por satélite y, especialmente, el Sistema de Posicionamiento Global ganaron importancia, se desarrollaron verdaderos modelos globales que, si bien no son tan precisos para el trabajo regional, se aproximan mejor a la Tierra en su conjunto.

Los siguientes radios se derivan del elipsoide de referencia del Sistema Geodésico Mundial de 1984 ( WGS-84 ) . ^[6] Es una superficie idealizada, y las mediciones terrestres utilizadas para calcularla tienen una incertidumbre de ±2 m tanto en la dimensión ecuatorial como en la polar. ^[7] Las discrepancias adicionales causadas por la variación topográfica en ubicaciones específicas pueden ser significativas. Al identificar la posición de una ubicación observable, el uso de valores más precisos para los radios WGS-84 puede no producir una mejora correspondiente en la precisión . ^{[ aclaración necesaria ]}

El valor del radio ecuatorial se define con una precisión de 0,1 m en WGS-84. El valor del radio polar en esta sección se ha redondeado a la precisión de 0,1 m, lo que se espera que sea adecuado para la mayoría de los usos. Consulte el elipsoide WGS-84 si necesita un valor más preciso para su radio polar.

• El radio ecuatorial de la Tierra a , o semieje mayor , ^{[8] : 11} es la distancia desde su centro hasta el ecuador y equivale a 6.378,1370 km (3.963,1906 mi). ^[9] El radio ecuatorial se utiliza a menudo para comparar la Tierra con otros planetas .

• El radio polar de la Tierra b , o semieje menor ^{[8] : 11,} es la distancia desde su centro a los polos Norte y Sur, y es igual a 6.356,7523 km (3.949,9028 mi).

El radio geocéntrico es la distancia desde el centro de la Tierra hasta un punto en la superficie del esferoide en la latitud geodésica φ , dada por la fórmula: ^[10]

${\displaystyle R(\varphi )={\sqrt {\frac {(a^{2}\cos \varphi )^{2}+(b^{2}\sin \varphi )^{2}}{(a\cos \varphi )^{2}+(b\sin \varphi )^{2}}}},}$

donde a y b son, respectivamente, el radio ecuatorial y el radio polar.

Los radios geocéntricos extremos del elipsoide coinciden con los radios ecuatorial y polar. Son los vértices de la elipse y también coinciden con los radios de curvatura mínimo y máximo.

Hay dos radios de curvatura principales : a lo largo de las secciones normales meridionales y verticales principales .

En particular, el radio de curvatura meridional de la Tierra (en dirección norte-sur) en φ es: ^[11]

${\displaystyle M(\varphi )={\frac {(ab)^{2}}{{\big (}(a\cos \varphi )^{2}+(b\sin \varphi )^{2}{\big )}^{\frac {3}{2}}}}={\frac {a(1-e^{2})}{(1-e^{2}\sin ^{2}\varphi )^{\frac {3}{2}}}}={\frac {1-e^{2}}{a^{2}}}N(\varphi )^{3}\,.}$

¿Dónde está la excentricidad de la Tierra? Este es el radio que Eratóstenes midió en su medición de arco .${\displaystyle e}$

Si un punto hubiera aparecido exactamente al este del otro, se encontraría la curvatura aproximada en dirección este-oeste. ^[f]

El radio de curvatura vertical principal de la Tierra , también llamado radio de curvatura transversal de la Tierra , se define perpendicular ( ortogonal ) a M en la latitud geodésica φ ^[g] y es: ^[11]

${\displaystyle N(\varphi )={\frac {a^{2}}{\sqrt {(a\cos \varphi )^{2}+(b\sin \varphi )^{2}}}}={\frac {a}{\sqrt {1-e^{2}\sin ^{2}\varphi }}}\,.}$

N también puede interpretarse geométricamente como la distancia normal desde la superficie del elipsoide hasta el eje polar. ^[12] El radio de un paralelo de latitud está dado por . ^{[13] [14]}${\displaystyle p=N\cos(\varphi )}$

El radio de curvatura meridional de la Tierra en el ecuador es igual al semilato recto del meridiano :

Yo = ⁠_​el segundo ²/a⁠  = 6.335,439 kilómetros

El radio de curvatura vertical principal de la Tierra en el ecuador es igual al radio ecuatorial, N _e = a .

El radio de curvatura polar de la Tierra (ya sea meridional o vertical principal) es:

M _p = N _p = ⁠un ²/b⁠  = 6.399,594 kilómetros

El radio de curvatura azimutal de la Tierra , a lo largo de una sección normal a la Tierra en un acimut (medido en el sentido de las agujas del reloj desde el norte) α y en una latitud φ , se deriva de la fórmula de curvatura de Euler de la siguiente manera: ^{[16] : 97}

${\displaystyle R_{\mathrm {c} }={\frac {1}{{\dfrac {\cos ^{2}\alpha }{M}}+{\dfrac {\sin ^{2}\alpha }{N}}}}\,.}$

Es posible combinar los principales radios de curvatura anteriores de manera no direccional.

El radio de curvatura gaussiano de la Tierra en la latitud φ es: ^[16]

${\displaystyle R_{\mathrm {a} }(\varphi )={\frac {1}{\sqrt {K}}}={\frac {1}{2\pi }}\int _{0}^{2\pi }R_{\mathrm {c} }(\alpha )\,d\alpha \,={\sqrt {MN}}={\frac {a^{2}b}{(a\cos \varphi )^{2}+(b\sin \varphi )^{2}}}={\frac {a{\sqrt {1-e^{2}}}}{1-e^{2}\sin ^{2}\varphi }}\,.}$

Donde K es la curvatura gaussiana , .${\displaystyle K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\det \,A}}}$

El radio de curvatura medio de la Tierra en la latitud φ es: ^{[16] : 97}

${\displaystyle R_{\mathrm {m} }={\frac {2}{{\dfrac {1}{M}}+{\dfrac {1}{N}}}}\,\!}$

La Tierra se puede modelar como una esfera de muchas maneras. Esta sección describe las formas más comunes. Los diversos radios que se derivan aquí utilizan la notación y las dimensiones indicadas anteriormente para la Tierra, derivadas del elipsoide WGS-84 ; ^[6] a saber,

Radio ecuatorial : a = (6 378,1370 kilómetros )

Radio polar : b = (6 356,7523 kilómetros )

Como una esfera es una aproximación aproximada del esferoide, que a su vez es una aproximación del geoide, las unidades se dan aquí en kilómetros en lugar de la resolución milimétrica apropiada para la geodesia.

En geofísica, la Unión Internacional de Geodesia y Geofísica (IUGG) define el radio medio aritmético de la Tierra (denominado R ₁ ) como ^[2]

${\displaystyle R_{1}={\frac {2a+b}{3}}\,\!}$

El factor dos explica la simetría biaxial del esferoide terrestre, una especialización del elipsoide triaxial. En el caso de la Tierra, el radio medio aritmético es de 6.371,0088 km (3.958,7613 mi). ^[17]

El radio autálico de la Tierra (que significa "área igual" ) es el radio de una esfera perfecta hipotética que tiene la misma área de superficie que el elipsoide de referencia . La IUGG denota el radio autálico como R ₂ . ^[2] Existe una solución de forma cerrada para un esferoide: ^[8]

${\displaystyle R_{2}={\sqrt {{\frac {1}{2}}\left(a^{2}+{\frac {b^{2}}{e}}\ln {\frac {1+e}{b/a}}\right)}}={\sqrt {{\frac {a^{2}}{2}}+{\frac {b^{2}}{2}}{\frac {\tanh ^{-1}e}{e}}}}={\sqrt {\frac {A}{4\pi }}}\,,}$

donde ⁠ ⁠${\displaystyle \textstyle e={\sqrt {a^{2}-b^{2}}}{\big /}a}$ es la excentricidad y ⁠ ⁠${\displaystyle A}$ es el área superficial del esferoide.

Para la Tierra, el radio autálico es 6.371,0072 km (3.958,7603 mi). ^[17]

El radio autálico también corresponde al radio de curvatura media (global) , obtenido promediando la curvatura gaussiana, , sobre la superficie del elipsoide. Utilizando el teorema de Gauss-Bonnet , esto da${\displaystyle R_{2}}$${\displaystyle K}$

${\displaystyle {\frac {\int K\,dA}{A}}={\frac {4\pi }{A}}={\frac {1}{R_{2}^{2}}}.}$

Otro modelo esférico se define por el radio volumétrico de la Tierra , que es el radio de una esfera de volumen igual al elipsoide. La IUGG denota el radio volumétrico como R ₃ . ^[2]

${\displaystyle R_{3}={\sqrt[{3}]{a^{2}b}}\,.}$

Para la Tierra, el radio volumétrico equivale a 6.371,0008 km (3.958,7564 mi). ^[17]

Otro radio global es el radio rectificador de la Tierra , que da como resultado una esfera con una circunferencia igual al perímetro de la elipse descrita por cualquier sección transversal polar del elipsoide. Esto requiere una integral elíptica para encontrar, dados los radios polar y ecuatorial:

${\displaystyle M_{\mathrm {r} }={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}{\sqrt {{a^{2}}\cos ^{2}\varphi +{b^{2}}\sin ^{2}\varphi }}\,d\varphi \,.}$

El radio de rectificación es equivalente a la media meridional, que se define como el valor promedio de M : ^[8]

${\displaystyle M_{\mathrm {r} }={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\!M(\varphi )\,d\varphi \,.}$

Para límites de integración de [0, ⁠π/2⁠ ], las integrales del radio de rectificación y del radio medio evalúan el mismo resultado, que, para la Tierra, asciende a 6.367,4491 km (3.956,5494 mi).

La media meridional se aproxima bien mediante la media semicúbica de los dos ejes, ^{[ cita requerida ]}

${\displaystyle M_{\mathrm {r} }\approx \left({\frac {a^{\frac {3}{2}}+b^{\frac {3}{2}}}{2}}\right)^{\frac {2}{3}}\,,}$

que difiere del resultado exacto en menos de 1 μm (4 × 10 ⁻⁵  in); la media de los dos ejes,

${\displaystyle M_{\mathrm {r} }\approx {\frac {a+b}{2}}\,,}$

También se puede utilizar una distancia de aproximadamente 6.367,445 km (3.956,547 mi).

Las expresiones matemáticas anteriores se aplican a la superficie del elipsoide. Los casos siguientes consideran la topografía de la Tierra , por encima o por debajo de un elipsoide de referencia . Como tales, son distancias geocéntricas topográficas , R _t , que no dependen solo de la latitud.

• R _t máxima : la cumbre del Chimborazo está a 6.384,4 km (3.967,1 mi) del centro de la Tierra.
• R _t mínimo : el fondo del océano Ártico está a 6.352,8 km (3.947,4 mi) del centro de la Tierra. ^[18]

La distancia geocéntrica media topográfica promedia las elevaciones en todas partes, lo que da como resultado un valor230 m mayor que el radio medio de la IUGG, el radio autálico o el radio volumétrico. Este promedio topográfico es de 6.371,230 km (3.958,899 mi) con una incertidumbre de 10 m (33 ft). ^[19]

El diámetro de la Tierra es simplemente el doble del radio de la Tierra; por ejemplo, el diámetro ecuatorial (2 a ) y el diámetro polar (2 b ). Para el elipsoide WGS84, son respectivamente:

• 2 a = 12.756,2740 km (7.926,3812 mi) ,
• 2b = 12.713,5046 km (7.899,8055 millas) .

La circunferencia de la Tierra es igual a la longitud del perímetro . La circunferencia ecuatorial es simplemente el perímetro del círculo : C _e = 2 πa , en términos del radio ecuatorial, a . La circunferencia polar es igual a C _p = 4 m _p , cuatro veces el cuarto meridiano m _p = aE ( e ), donde el radio polar b entra por la excentricidad, e = (1− b ² / a ² ) ^0,5 ; consulte Elipse#Circunferencia para obtener más detalles.

La longitud del arco de curvas superficiales más generales , como los arcos meridianos y las geodésicas , también se puede derivar de los radios ecuatoriales y polares de la Tierra.

Lo mismo ocurre con el área de superficie , ya sea basada en una proyección cartográfica o en un polígono geodésico .

El volumen de la Tierra , o el del elipsoide de referencia, es V = ⁠4/3⁠ π a ² b . Utilizando los parámetros delelipsoide de revolución WGS84 , a = 6.378,137 km y b =6 356 0,752 3142  km , V = 1,08321 × 10 ¹²  km ³ (2,5988 × 10 ¹¹  millas cúbicas) . ^[20]

En astronomía, la Unión Astronómica Internacional denota el radio ecuatorial nominal de la Tierra como , que se define exactamente como 6.378,1 km (3.963,2 mi). ^{[1] : 3} El radio polar nominal de la Tierra se define exactamente como = 6.356,8 km (3.949,9 mi). Estos valores corresponden a la convención de marea terrestre cero . El radio ecuatorial se utiliza convencionalmente como el valor nominal a menos que se requiera explícitamente el radio polar. ^{[1] : 4} El radio nominal sirve como unidad de longitud para astronomía . (La notación se define de tal manera que se puede generalizar fácilmente para otros planetas ; por ejemplo, para el radio polar nominal de Júpiter ).${\displaystyle {\mathcal {R}}_{e\mathrm {E} }^{\mathrm {N} }}$${\displaystyle {\mathcal {R}}_{p\mathrm {E} }^{\mathrm {N} }}$${\displaystyle {\mathcal {R}}_{p\mathrm {J} }^{\mathrm {N} }}$

Esta tabla resume los valores aceptados del radio de la Tierra.

La primera referencia publicada sobre el tamaño de la Tierra apareció alrededor del 350  a. C. , cuando Aristóteles informó en su libro Sobre los cielos ^[22] que los matemáticos habían calculado que la circunferencia de la Tierra era de 400.000 estadios . Los académicos han interpretado que la cifra de Aristóteles es desde muy precisa ^[23] hasta casi el doble del valor real. ^[24] La primera medición y cálculo científico conocido de la circunferencia de la Tierra fue realizado por Eratóstenes alrededor del 240 a. C. Las estimaciones del error de la medición de Eratóstenes varían del 0,5% al ​​17%. ^[25] Tanto para Aristóteles como para Eratóstenes, la incertidumbre en la precisión de sus estimaciones se debe a la incertidumbre moderna sobre a qué longitud de estadio se referían.

Alrededor del año 100 a. C., Posidonio de Apamea volvió a calcular el radio de la Tierra y descubrió que era cercano al de Eratóstenes, ^[26] pero más tarde Estrabón le atribuyó incorrectamente un valor de aproximadamente 3/4 del tamaño real. ^[27] Claudio Ptolomeo alrededor del año 150  d. C. proporcionó evidencia empírica que respaldaba la idea de que la Tierra era esférica , ^[28] pero aceptó el valor menor atribuido a Posidonio. Su obra muy influyente, el Almagesto , ^[29] no dejó dudas entre los eruditos medievales de que la Tierra es esférica, pero se equivocaron sobre su tamaño.

En 1490, Cristóbal Colón creía que viajar 3.000 millas al oeste desde la costa oeste de la península Ibérica le permitiría llegar a las costas orientales de Asia . ^[30] Sin embargo, la promulgación de ese viaje en 1492 llevó a su flota a las Américas . La expedición de Magallanes (1519-1522), que fue la primera circunnavegación del mundo, demostró sólidamente la esfericidad de la Tierra, ^[31] y afirmó la medida original de 40.000 km (25.000 mi) de Eratóstenes.

Alrededor de 1690, Isaac Newton y Christiaan Huygens argumentaron que la Tierra estaba más cerca de un esferoide achatado que de una esfera. Sin embargo, alrededor de 1730, Jacques Cassini argumentó que en cambio era un esferoide alargado , debido a las diferentes interpretaciones de la mecánica newtoniana involucradas. ^[32] Para resolver el asunto, la Misión Geodésica Francesa (1735-1739) midió un grado de latitud en dos lugares, uno cerca del Círculo Polar Ártico y el otro cerca del ecuador . La expedición descubrió que la conjetura de Newton era correcta: ^[33] la Tierra está achatada en los polos debido a la fuerza centrífuga de rotación .

Wikisource tiene el texto del artículo de la Encyclopædia Britannica de 1911 " Tierra, figura de la ".

• Merrifield, Michael R. (2010). " R ⊕ {\displaystyle R_{\oplus }} El radio de la Tierra (y los exoplanetas)". Sesenta símbolos . Brady Haran para la Universidad de Nottingham .

Wikimedia Commons tiene medios relacionados con Radio de la Tierra .