Circunferencia

Geometría
Proyectar una esfera a un plano
Describir Historia ( Cronología )
Sucursales Euclidiano No euclidiano Elíptico Esférico Hiperbólico Non-Archimedean geometry Projective Affine Synthetic Analytic Algebraic Arithmetic Diophantine Differential Riemannian Symplectic Discrete differential Complex Finite Discrete/Combinatorial Digital Convex Computational Fractal Incidence Noncommutative geometry Noncommutative algebraic geometry
Concepts Features Dimension Straightedge and compass constructions Angle Curve Diagonal Orthogonality (Perpendicular) Parallel Vertex Congruence Similarity Symmetry
Zero-dimensional Point
One-dimensional Line segment ray Length
Two-dimensional Plane Area Polygon Triangle Altitude Hypotenuse Pythagorean theorem Parallelogram Square Rectangle Rhombus Rhomboid Quadrilateral Trapezoid Kite Circle Diameter Circumference Area
Three-dimensional Volume Cube cuboid Cylinder Dodecahedron Icosahedron Octahedron Pyramid Platonic Solid Sphere Tetrahedron
Four- / other-dimensional Tesseract Hypersphere
Geometers
by name Aida Aryabhata Ahmes Alhazen Apollonius Archimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euclid Euler Gauss Gromov Hilbert Huygens Jyeṣṭhadeva Kātyāyana Khayyám Klein Lobachevsky Manava Minkowski Minggatu Pascal Pythagoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang List of geometers
by period BCE Ahmes Baudhayana Manava Pythagoras Euclid Archimedes Apollonius 1–1400s Zhang Kātyāyana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyám al-Yasamin al-Tusi Yang Hui Parameshvara 1400s–1700s Jyeṣṭhadeva Descartes Pascal Huygens Minggatu Euler Sakabe Aida 1700s–1900s Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Present day Atiyah Gromov
v t e

En geometría , la circunferencia (del latín circumferens , que significa "que lleva alrededor") es el perímetro de un círculo o una elipse . La circunferencia es la longitud del arco del círculo, como si se abriera y se enderezara hasta convertirse en un segmento de línea . ^[1] De manera más general, el perímetro es la longitud de la curva alrededor de cualquier figura cerrada. La circunferencia también puede referirse al círculo en sí, es decir, al lugar geométrico correspondiente al borde de un disco .La circunferencia de una esfera es la circunferencia o longitud de cualquiera de suscírculos máximos.

La circunferencia de un círculo es la distancia que lo rodea, pero si, como en muchos tratamientos elementales, la distancia se define en términos de líneas rectas, esto no puede usarse como definición. En estas circunstancias, la circunferencia de un círculo puede definirse como el límite de los perímetros de polígonos regulares inscritos a medida que el número de lados aumenta sin límite. ^[2] El término circunferencia se utiliza al medir objetos físicos, así como al considerar formas geométricas abstractas.

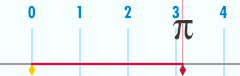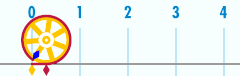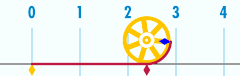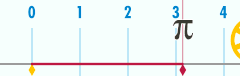
La circunferencia de un círculo está relacionada con una de las constantes matemáticas más importantes . Esta constante , pi , se representa con la letra griega Sus primeros dígitos decimales son 3,141592653589793... ^[3] . Pi se define como la relación entre la circunferencia de un círculo y su diámetro.${\displaystyle \pi .}$${\displaystyle C}$ ${\displaystyle d:}$$${\displaystyle \pi ={\frac {C}{d}}.}$$

O, equivalentemente, como la relación entre la circunferencia y el doble del radio . La fórmula anterior se puede reorganizar para obtener la circunferencia:$${\displaystyle {C}=\pi \cdot {d}=2\pi \cdot {r}.\!}$$

La relación entre la circunferencia del círculo y su radio es equivalente a . ^[a] Este es también el número de radianes en una vuelta . El uso de la constante matemática π es omnipresente en matemáticas, ingeniería y ciencia.${\displaystyle 2\pi }$

En Medición de un círculo escrito alrededor del año 250 a. C., Arquímedes demostró que esta relación (escrita como π ya que no utilizó el nombre ) era mayor que 3 .${\displaystyle C/d,}$10/71⁠ pero menos de 3 ⁠1/7⁠ calculando los perímetros de un polígono regular inscrito y circunscrito de 96 lados. ^[8] Este método para aproximar π se utilizó durante siglos, obteniéndose más precisión al utilizar polígonos de mayor y mayor número de lados. El último cálculo de este tipo lo realizó en 1630 Christoph Grienberger, que utilizó polígonos con 10 ⁴⁰ lados.

Algunos autores utilizan la circunferencia para denotar el perímetro de una elipse. No existe una fórmula general para la circunferencia de una elipse en términos de los semiejes mayor y menor de la elipse que utilice solo funciones elementales. Sin embargo, existen fórmulas aproximadas en términos de estos parámetros. Una de esas aproximaciones, debida a Euler (1773), para la elipse canónica , es Algunos límites inferiores y superiores de la circunferencia de la elipse canónica son: ^[9]$${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,}$$$${\displaystyle C_{\rm {ellipse}}\sim \pi {\sqrt {2\left(a^{2}+b^{2}\right)}}.}$$${\displaystyle a\geq b}$$${\displaystyle 2\pi b\leq C\leq 2\pi a,}$$$${\displaystyle \pi (a+b)\leq C\leq 4(a+b),}$$$${\displaystyle 4{\sqrt {a^{2}+b^{2}}}\leq C\leq \pi {\sqrt {2\left(a^{2}+b^{2}\right)}}.}$$

Aquí el límite superior es la circunferencia de un círculo concéntrico circunscrito que pasa por los puntos finales del eje mayor de la elipse, y el límite inferior es el perímetro de un rombo inscrito con vértices en los puntos finales de los ejes mayor y menor.${\displaystyle 2\pi a}$ ${\displaystyle 4{\sqrt {a^{2}+b^{2}}}}$

La circunferencia de una elipse se puede expresar exactamente en términos de la integral elíptica completa de segundo tipo . ^[10] Más precisamente, donde es la longitud del semieje mayor y es la excentricidad.$${\displaystyle C_{\rm {ellipse}}=4a\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta ,}$$${\displaystyle a}$${\displaystyle e}$${\displaystyle {\sqrt {1-b^{2}/a^{2}}}.}$

• Longitud del arco  : distancia a lo largo de una curva
• Área  – Tamaño de una superficie bidimensional
• Circungono  – Figura geométrica que circunscribe un círculo.
• Desigualdad isoperimétrica  : desigualdad geométrica que establece un límite inferior para el área de superficie de un conjunto dado su volumen.
• Radio equivalente al perímetro  : radio de un círculo o esfera equivalente a un objeto no circular o no esféricoPages displaying short descriptions of redirect targets

El Wikilibro Geometría tiene una página sobre el tema: Arcos

Busque circunferencia en Wikcionario, el diccionario libre.

• Numericana - Circunferencia de una elipse