Geometría molecular

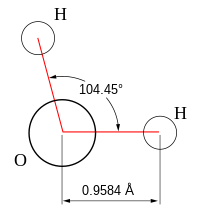
La geometría molecular es la disposición tridimensional de los átomos que constituyen una molécula . Incluye la forma general de la molécula, así como las longitudes de enlace , los ángulos de enlace , los ángulos de torsión y cualquier otro parámetro geométrico que determine la posición de cada átomo.

La geometría molecular influye en varias propiedades de una sustancia, incluyendo su reactividad , polaridad , fase de la materia , color , magnetismo y actividad biológica . ^{[1] [2] [3]} Los ángulos entre los enlaces que forma un átomo dependen sólo débilmente del resto de la molécula, es decir, pueden entenderse como propiedades aproximadamente locales y, por tanto, transferibles .

La geometría molecular se puede determinar mediante varios métodos espectroscópicos y métodos de difracción . La espectroscopia IR , de microondas y Raman puede proporcionar información sobre la geometría de la molécula a partir de los detalles de la absorbancia vibracional y rotacional detectada por estas técnicas. La cristalografía de rayos X , la difracción de neutrones y la difracción de electrones pueden proporcionar la estructura molecular de los sólidos cristalinos basándose en la distancia entre los núcleos y la concentración de la densidad electrónica. La difracción de electrones de gas se puede utilizar para moléculas pequeñas en la fase gaseosa. Los métodos de RMN y FRET se pueden utilizar para determinar información complementaria, incluidas las distancias relativas, ^{[4] [5] [6]} ángulos diedros, ^{[7] [8]} ángulos y conectividad. Las geometrías moleculares se determinan mejor a baja temperatura porque a temperaturas más altas la estructura molecular se promedia sobre geometrías más accesibles (ver la siguiente sección). Las moléculas más grandes a menudo existen en múltiples geometrías estables ( isomería conformacional ) que están cerca en energía en la superficie de energía potencial . Las geometrías también se pueden calcular con métodos de química cuántica ab initio con gran precisión. La geometría molecular puede ser diferente en estado sólido, en solución y en estado gaseoso.

La posición de cada átomo está determinada por la naturaleza de los enlaces químicos que lo unen a sus átomos vecinos. La geometría molecular se puede describir por las posiciones de estos átomos en el espacio, evocando longitudes de enlace de dos átomos unidos, ángulos de enlace de tres átomos conectados y ángulos de torsión ( ángulos diedros ) de tres enlaces consecutivos .

Dado que los movimientos de los átomos en una molécula están determinados por la mecánica cuántica, el "movimiento" debe definirse de una manera mecánico-cuántica. Los movimientos mecánicos cuánticos generales (externos) de traslación y rotación apenas modifican la geometría de la molécula. (Hasta cierto punto, la rotación influye en la geometría a través de las fuerzas de Coriolis y la distorsión centrífuga , pero esto es insignificante para la presente discusión). Además de la traslación y la rotación, un tercer tipo de movimiento es la vibración molecular , que corresponde a los movimientos internos de los átomos, como el estiramiento de los enlaces y la variación del ángulo de enlace. Las vibraciones moleculares son armónicas (al menos en una buena aproximación), y los átomos oscilan alrededor de sus posiciones de equilibrio, incluso en el cero absoluto de temperatura. En el cero absoluto, todos los átomos están en su estado fundamental vibracional y muestran un movimiento mecánico cuántico de punto cero , de modo que la función de onda de un solo modo vibracional no es un pico agudo, sino aproximadamente una función gaussiana (la función de onda para n  = 0 se muestra en el artículo sobre el oscilador armónico cuántico ). A temperaturas más altas, los modos vibracionales pueden excitarse térmicamente (en una interpretación clásica esto se expresa diciendo que "las moléculas vibrarán más rápido"), pero aún oscilan alrededor de la geometría reconocible de la molécula.

Para tener una idea de la probabilidad de que la vibración de la molécula pueda ser excitada térmicamente, inspeccionamos el factor de Boltzmann β ≡ exp(− ⁠ΔE​/kT⁠ ) ​​, donde Δ E es la energía de excitación del modo vibracional, k la constante de Boltzmann y T la temperatura absoluta. A 298 K (25 °C), los valores típicos para el factor de Boltzmann β son:

• β = 0,089 0 para Δ E = 0 500 cm ⁻¹
• β = 0,008 0 para Δ E = 1000 cm ⁻¹
• β = 0,0007 para Δ E = 1500 cm ⁻¹ .

(El centímetro recíproco es una unidad de energía que se utiliza comúnmente en espectroscopia infrarroja ; 1 cm ⁻¹ corresponde a1.239 84 × 10 ⁻⁴  eV ). Cuando una energía de excitación es de 500 cm ⁻¹ , entonces aproximadamente el 8,9 por ciento de las moléculas están excitadas térmicamente a temperatura ambiente. Para poner esto en perspectiva: la energía vibracional de excitación más baja en el agua es el modo de flexión (alrededor de 1600 cm ⁻¹ ). Por lo tanto, a temperatura ambiente, menos del 0,07 por ciento de todas las moléculas de una cantidad dada de agua vibrarán más rápido que en el cero absoluto.

Como se ha dicho antes, la rotación apenas influye en la geometría molecular. Pero, como movimiento mecánico cuántico, se excita térmicamente a temperaturas relativamente bajas (en comparación con la vibración). Desde un punto de vista clásico, se puede afirmar que a temperaturas más altas, más moléculas rotarán más rápido, lo que implica que tienen mayor velocidad angular y momento angular . En lenguaje mecánico cuántico: más estados propios de mayor momento angular se pueblan térmicamente con temperaturas crecientes. Las energías de excitación rotacional típicas son del orden de unos pocos cm ⁻¹ . Los resultados de muchos experimentos espectroscópicos se amplían porque implican un promedio sobre estados rotacionales. A menudo es difícil extraer geometrías de espectros a altas temperaturas, porque el número de estados rotacionales investigados en el promedio experimental aumenta con el aumento de la temperatura. Por lo tanto, solo se puede esperar que muchas observaciones espectroscópicas produzcan geometrías moleculares confiables a temperaturas cercanas al cero absoluto, porque a temperaturas más altas se pueblan térmicamente demasiados estados rotacionales más altos.

Las moléculas, por definición, suelen mantenerse unidas mediante enlaces covalentes que implican enlaces simples, dobles y/o triples, donde un "enlace" es un par de electrones compartidos (el otro método de enlace entre átomos se denomina enlace iónico e implica un catión positivo y un anión negativo ).

Las geometrías moleculares se pueden especificar en términos de "longitudes de enlace", "ángulos de enlace" y "ángulos de torsión". La longitud de enlace se define como la distancia promedio entre los núcleos de dos átomos unidos entre sí en una molécula dada. Un ángulo de enlace es el ángulo formado entre tres átomos a través de al menos dos enlaces. Para cuatro átomos unidos entre sí en una cadena, el ángulo de torsión es el ángulo entre el plano formado por los primeros tres átomos y el plano formado por los últimos tres átomos.

Existe una relación matemática entre los ángulos de enlace de un átomo central y cuatro átomos periféricos (etiquetados del 1 al 4) expresada por el siguiente determinante. Esta restricción elimina un grado de libertad de las opciones de (originalmente) seis ángulos de enlace libres para dejar solo cinco opciones de ángulos de enlace. (Los ángulos θ ₁₁ , θ ₂₂ , θ ₃₃ y θ ₄₄ son siempre cero y esta relación se puede modificar para un número diferente de átomos periféricos expandiendo/contrayendo la matriz cuadrada).

${\displaystyle 0={\begin{vmatrix}\cos \theta _{11}&\cos \theta _{12}&\cos \theta _{13}&\cos \theta _{14}\\\cos \theta _{21}&\cos \theta _{22}&\cos \theta _{23}&\cos \theta _{24}\\\cos \theta _{31}&\cos \theta _{32}&\cos \theta _{33}&\cos \theta _{34}\\\cos \theta _{41}&\cos \theta _{42}&\cos \theta _{43}&\cos \theta _{44}\end{vmatrix}}}$

La geometría molecular está determinada por el comportamiento mecánico cuántico de los electrones. Utilizando la aproximación del enlace de valencia, esto se puede entender por el tipo de enlaces entre los átomos que forman la molécula. Cuando los átomos interactúan para formar un enlace químico , se dice que los orbitales atómicos de cada átomo se combinan en un proceso llamado hibridación orbital . Los dos tipos de enlaces más comunes son los enlaces sigma (generalmente formados por orbitales híbridos) y los enlaces pi (formados por orbitales p no hibridados para átomos de elementos del grupo principal ). La geometría también se puede entender mediante la teoría de orbitales moleculares donde los electrones están deslocalizados.

La comprensión del comportamiento ondulatorio de los electrones en átomos y moléculas es el tema de la química cuántica .

Los isómeros son tipos de moléculas que comparten una fórmula química pero tienen geometrías diferentes, lo que da como resultado propiedades diferentes:

• Una sustancia pura está compuesta por un solo tipo de isómero de una molécula (todos tienen la misma estructura geométrica).
• Los isómeros estructurales tienen la misma fórmula química pero diferentes disposiciones físicas, y a menudo forman geometrías moleculares alternativas con propiedades muy diferentes. Los átomos no están unidos (conectados) entre sí en el mismo orden.
  • Los isómeros funcionales son tipos especiales de isómeros estructurales, donde ciertos grupos de átomos exhiben un tipo especial de comportamiento, como un éter o un alcohol.
• Los estereoisómeros pueden tener muchas propiedades fisicoquímicas similares (punto de fusión, punto de ebullición) y, al mismo tiempo, actividades bioquímicas muy diferentes . Esto se debe a que presentan una quiralidad o lateralidad que se encuentra comúnmente en los sistemas vivos. Una manifestación de esta quiralidad o lateralidad es que tienen la capacidad de rotar la luz polarizada en diferentes direcciones.
• El plegamiento de proteínas se refiere a las geometrías complejas y los diferentes isómeros que pueden adoptar las proteínas .

Un ángulo de enlace es el ángulo geométrico entre dos enlaces adyacentes. Algunas formas comunes de moléculas simples incluyen:

• Lineal : en un modelo lineal, los átomos están conectados en línea recta. Los ángulos de enlace se establecen en 180°. Por ejemplo, el dióxido de carbono y el óxido nítrico tienen una forma molecular lineal.
• Trigonal plana : Las moléculas con forma trigonal plana son más bien triangulares y están en un plano (planas) . En consecuencia, los ángulos de enlace se establecen en 120°. Por ejemplo, el trifluoruro de boro .
• Angular : Las moléculas angulares (también llamadas curvas o en forma de V ) tienen una forma no lineal. Por ejemplo, el agua (H2O ₎ , que tiene un ángulo de aproximadamente 105°. Una molécula de agua tiene dos pares de electrones enlazados y dos pares solitarios no compartidos.
• Tetraédrico : Tetra- significa cuatro, y -édrico se relaciona con una cara de un sólido, por lo que " tetraédrico " significa literalmente "que tiene cuatro caras". Esta forma se encuentra cuando hay cuatro enlaces, todos en un átomo central , sin pares de electrones adicionales no compartidos . De acuerdo con la teoría de repulsión de pares de electrones de la capa de valencia ( VSEPR ), los ángulos de enlace entre los enlaces de electrones son arcocos (− ⁠1/3⁠ ) ​​= 109,47°. Por ejemplo, el metano (CH ₄ ) es una molécula tetraédrica.
• Octaédrico : octa- significa ocho y -édrico se relaciona con una cara de un sólido, por lo que " octaédrico " significa "que tiene ocho caras". El ángulo de enlace es de 90 grados. Por ejemplo, el hexafluoruro de azufre (SF6 ₎ es una molécula octaédrica.
• Pirámide trigonal : una molécula piramidal trigonal tiene una forma similar a una pirámide con una base triangular. A diferencia de las formas planas lineales y trigonales, pero similares a la orientación tetraédrica, las formas piramidales requieren tres dimensiones para separar completamente los electrones. Aquí, solo hay tres pares de electrones enlazados, dejando un par solitario sin compartir. Las repulsiones entre pares solitarios y pares enlazados cambian el ángulo de enlace del ángulo tetraédrico a un valor ligeramente inferior. ^[9] Por ejemplo, amoníaco (NH ₃ ).

Los ángulos de enlace de la tabla siguiente son ángulos ideales de la teoría VSEPR simple (pronunciada "Teoría de Vesper") ^{[ cita requerida ]} , seguidos del ángulo real para el ejemplo dado en la siguiente columna donde difiere. Para muchos casos, como la pirámide trigonal y la curva, el ángulo real para el ejemplo difiere del ángulo ideal, y los ejemplos difieren en diferentes cantidades. Por ejemplo, el ángulo en H ₂ S (92°) difiere del ángulo tetraédrico en mucho más que el ángulo para H ₂ O (104,48°).

Átomos unidos al átomo central	Pares solitarios	Dominios electrónicos (número estérico)	Forma	Ángulo de enlace ideal (ángulo de enlace de ejemplo)	Ejemplo	Imagen
2	0	2	lineal	180°	CO2​
3	0	3	plano trigonal	120°	BF3​
2	1	3	doblado	120° (119°)	SO 2
4	0	4	tetraédrico	109,5°	Capítulo 4
3	1	4	piramidal trigonal	109,5° (106,8°) [10]	NH3​
2	2	4	doblado	109,5° (104,48°) [11] [12]	H2O​​
5	0	5	bipiramidal trigonal	90°, 120°	PCl5​
4	1	5	balancín	ax–ax 180° (173,1°), eq–eq 120° (101,6°), ax–eq 90°	SF 4
3	2	5	En forma de T	90° (87,5°), 180° (175°)	ClF3​
2	3	5	lineal	180°	XeF2​
6	0	6	octaédrico	90°, 180°	SF6​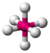
5	1	6	pirámide cuadrada	90° (84,8°)	BRF5​
4	2	6	plano cuadrado	90°, 180°	XeF4​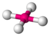
7	0	7	bipiramidal pentagonal	90°, 72°, 180°	SI 7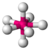
6	1	7	piramidal pentagonal	72°, 90°, 144°	XeOF−5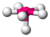
5	2	7	plano pentagonal	72°, 144°	XeF−5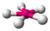
8	0	8	antiprismático cuadrado		XeF2−8
9	0	9	prismático trigonal tricapa		ReH2−9

• Línea o barra : no se representan los núcleos atómicos, solo los enlaces como barras o líneas. Como en las estructuras moleculares 2D de este tipo, los átomos están implícitos en cada vértice.

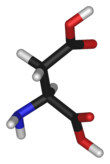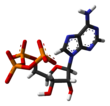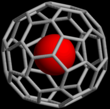• Gráfico de densidad electrónica : muestra la densidad electrónica determinada cristalográficamente o utilizando mecánica cuántica en lugar de átomos o enlaces distintos.

• Bolas y palos : los núcleos atómicos están representados por esferas (bolas) y los enlaces como palos.

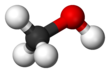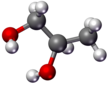• Modelos de relleno espacial o modelos CPK (también un esquema de coloración atómica en las representaciones): la molécula está representada por esferas superpuestas que representan los átomos.

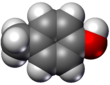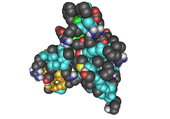• Caricatura : representación utilizada para proteínas donde los bucles, las láminas beta y las hélices alfa se representan en forma de diagrama y no se representan explícitamente átomos ni enlaces (por ejemplo, la estructura principal de la proteína se representa como un tubo liso).

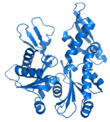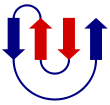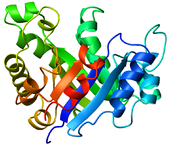Cuanto mayor sea la cantidad de pares solitarios que contiene una molécula, menores serán los ángulos entre los átomos de esa molécula. La teoría VSEPR predice que los pares solitarios se repelen entre sí, alejando así a los diferentes átomos de ellos.

Wikimedia Commons tiene medios relacionados con Geometría molecular.

• Tutorial de geometría molecular y polaridad Visualización 3D de moléculas para determinar la polaridad.
• Geometría molecular utilizando cristales Visualización de la estructura 3D de moléculas mediante cristalografía.