Interferencia de ondas

Este artículo puede resultar demasiado técnico para que la mayoría de los lectores lo comprendan . Ayúdenos a mejorarlo para que sea comprensible para los no expertos , sin eliminar los detalles técnicos. ( Febrero de 2022 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En física , la interferencia es un fenómeno en el que dos ondas coherentes se combinan sumando sus intensidades o desplazamientos teniendo debidamente en cuenta su diferencia de fase . La onda resultante puede tener mayor intensidad ( interferencia constructiva ) o menor amplitud ( interferencia destructiva ) si las dos ondas están en fase o desfasadas, respectivamente. Los efectos de interferencia se pueden observar con todo tipo de ondas, por ejemplo, luz , radio , acústicas , ondas de superficie del agua , ondas de gravedad u ondas de materia , así como en altavoces como ondas eléctricas.

La palabra interferencia se deriva de las palabras latinas inter que significa "entre" y fere que significa "golpear o golpear", y fue utilizada en el contexto de la superposición de ondas por Thomas Young en 1801. ^{[1] [2] [3]}

El principio de superposición de ondas establece que cuando dos o más ondas del mismo tipo que se propagan inciden en el mismo punto, la amplitud resultante en ese punto es igual a la suma vectorial de las amplitudes de las ondas individuales. ^[4] Si la cresta de una onda se encuentra con la cresta de otra onda de la misma frecuencia en el mismo punto, entonces la amplitud es la suma de las amplitudes individuales; esto es interferencia constructiva. Si la cresta de una onda se encuentra con el valle de otra onda, entonces la amplitud es igual a la diferencia en las amplitudes individuales; esto se conoce como interferencia destructiva. En medios ideales (el agua y el aire son casi ideales) la energía siempre se conserva, en puntos de interferencia destructiva, las amplitudes de onda se cancelan entre sí y la energía se redistribuye a otras áreas. Por ejemplo, cuando se dejan caer dos piedras en un estanque, se observa un patrón; pero eventualmente las ondas continúan, y solo cuando llegan a la orilla la energía se absorbe fuera del medio.

La interferencia constructiva se produce cuando la diferencia de fase entre las ondas es un múltiplo par de π (180°), mientras que la interferencia destructiva se produce cuando la diferencia es un múltiplo impar de π . Si la diferencia entre las fases es intermedia entre estos dos extremos, entonces la magnitud del desplazamiento de las ondas sumadas se encuentra entre los valores mínimo y máximo.

Consideremos, por ejemplo, lo que ocurre cuando se dejan caer dos piedras idénticas en un estanque de agua quieta en diferentes lugares. Cada piedra genera una onda circular que se propaga hacia afuera desde el punto donde se dejó caer la piedra. Cuando las dos ondas se superponen, el desplazamiento neto en un punto determinado es la suma de los desplazamientos de las ondas individuales. En algunos puntos, estas estarán en fase y producirán un desplazamiento máximo. En otros lugares, las ondas estarán en contrafase y no habrá desplazamiento neto en estos puntos. Por lo tanto, partes de la superficie serán estacionarias; se ven en la figura de arriba y a la derecha como líneas estacionarias de color azul verdoso que irradian desde el centro.

La interferencia de la luz es un fenómeno único en el sentido de que nunca podemos observar la superposición del campo electromagnético directamente como, por ejemplo, en el agua. La superposición en el campo electromagnético es un fenómeno asumido y necesario para explicar cómo dos rayos de luz pasan uno a través del otro y continúan en sus respectivas trayectorias. Los principales ejemplos de interferencia de la luz son el famoso experimento de la doble rendija , el moteado láser , los recubrimientos antirreflectantes y los interferómetros .

Además del modelo de onda clásico para comprender la interferencia óptica, las ondas de materia cuántica también demuestran interferencia.

Lo anterior se puede demostrar en una dimensión derivando la fórmula para la suma de dos ondas. La ecuación para la amplitud de una onda sinusoidal que viaja hacia la derecha a lo largo del eje x es donde es la amplitud pico, es el número de onda y es la frecuencia angular de la onda. Supongamos que una segunda onda de la misma frecuencia y amplitud pero con una fase diferente también viaja hacia la derecha donde es la diferencia de fase entre las ondas en radianes . Las dos ondas se superpondrán y sumarán: la suma de las dos ondas es Usando la identidad trigonométrica para la suma de dos cosenos: esto se puede escribir Esto representa una onda en la frecuencia original, viajando hacia la derecha como sus componentes, cuya amplitud es proporcional al coseno de .$${\displaystyle W_{1}(x,t)=A\cos(kx-\omega t)}$$${\estilo de visualización A}$${\displaystyle k=2\pi /\lambda }$${\displaystyle \omega =2\pi f}$$${\displaystyle W_{2}(x,t)=A\cos(kx-\omega t+\varphi )}$$${\estilo de visualización \varphi}$$${\displaystyle W_{1}+W_{2}=A[\cos(kx-\omega t)+\cos(kx-\omega t+\varphi )].}$$${\textstyle \cos a+\cos b=2\cos \left({ab \sobre 2}\right)\cos \left({a+b \sobre 2}\right),}$$${\displaystyle W_{1}+W_{2}=2A\cos \left({\varphi \sobre 2}\right)\cos \left(kx-\omega t+{\varphi \sobre 2}\right).}$$${\estilo de visualización \varphi /2}$

• Interferencia constructiva : Si la diferencia de fase es un múltiplo par de π : entonces , por lo que la suma de las dos ondas es una onda con el doble de amplitud.${\displaystyle \varphi =\ldots ,-4\pi ,-2\pi ,0,2\pi ,4\pi ,\ldots }$${\displaystyle \left|\cos(\varphi /2)\right|=1}$$${\displaystyle W_{1}+W_{2}=2A\cos(kx-\omega t)}$$
• Interferencia destructiva : Si la diferencia de fase es un múltiplo impar de π : entonces , por lo que la suma de las dos ondas es cero${\displaystyle \varphi =\ldots ,-3\pi ,\,-\pi ,\,\pi ,\,3\pi ,\,5\pi ,\ldots }$${\displaystyle \cos(\varphi /2)=0\,}$$${\displaystyle W_{1}+W_{2}=0}$$

Se obtiene una forma simple de patrón de interferencia si dos ondas planas de la misma frecuencia se intersecan en un ángulo. Una onda viaja horizontalmente y la otra viaja hacia abajo en un ángulo θ con respecto a la primera onda. Suponiendo que las dos ondas están en fase en el punto B , entonces la fase relativa cambia a lo largo del eje x . La diferencia de fase en el punto A está dada por

$${\displaystyle \Delta \varphi ={\frac {2\pi d}{\lambda }}={\frac {2\pi x\sin \theta }{\lambda }}.}$$

Se puede ver que las dos ondas están en fase cuando

$${\displaystyle {\frac {x\sin \theta }{\lambda }}=0,\pm 1,\pm 2,\ldots ,}$$

y están desfasados ​​medio ciclo cuando

$${\displaystyle {\frac {x\sin \theta }{\lambda }}=\pm {\frac {1}{2}},\pm {\frac {3}{2}},\ldots }$$

La interferencia constructiva se produce cuando las ondas están en fase y la interferencia destructiva cuando están desfasadas medio ciclo. De este modo, se produce un patrón de franjas de interferencia, donde la separación de los máximos es

$${\displaystyle d_{f}={\frac {\lambda }{\sin \theta }}}$$

y d _f se conoce como el espaciado de franjas. El espaciado de franjas aumenta con el aumento de la longitud de onda y con la disminución del ángulo θ .

Las franjas se observan dondequiera que las dos ondas se superponen y el espaciado de las franjas es uniforme en todas partes.

Una fuente puntual produce una onda esférica. Si la luz de dos fuentes puntuales se superpone, el patrón de interferencia representa la forma en que varía en el espacio la diferencia de fase entre las dos ondas. Esto depende de la longitud de onda y de la separación de las fuentes puntuales. La figura de la derecha muestra la interferencia entre dos ondas esféricas. La longitud de onda aumenta de arriba hacia abajo y la distancia entre las fuentes aumenta de izquierda a derecha.

Cuando el plano de observación está lo suficientemente lejos, el patrón de franjas será una serie de líneas casi rectas, ya que las ondas serán entonces casi planas.

La interferencia se produce cuando se suman varias ondas siempre que las diferencias de fase entre ellas permanezcan constantes durante el tiempo de observación.

A veces es deseable que varias ondas de la misma frecuencia y amplitud sumen cero (es decir, que interfieran destructivamente, se cancelen). Este es el principio que subyace, por ejemplo, a la potencia trifásica y a la rejilla de difracción . En ambos casos, el resultado se consigue mediante un espaciado uniforme de las fases.

Es fácil ver que un conjunto de ondas se cancelará si tienen la misma amplitud y sus fases están espaciadas de manera uniforme en ángulo. Usando fasores , cada onda se puede representar como para ondas de a , donde${\displaystyle Ae^{i\varphi _{n}}}$${\displaystyle N}$${\displaystyle n=0}$${\displaystyle n=N-1}$$${\displaystyle \varphi _{n}-\varphi _{n-1}={\frac {2\pi }{N}}.}$$

Para demostrar que$${\displaystyle \sum _{n=0}^{N-1}Ae^{i\varphi _{n}}=0}$$

Uno simplemente asume lo contrario, luego multiplica ambos lados por${\displaystyle e^{i{\frac {2\pi }{N}}}.}$

El interferómetro de Fabry-Pérot utiliza la interferencia entre múltiples reflexiones.

Una rejilla de difracción puede considerarse un interferómetro de haces múltiples, ya que los picos que produce se generan por la interferencia entre la luz transmitida por cada uno de los elementos de la rejilla; consulte interferencia frente a difracción para obtener más información.

Las ondas mecánicas y gravitacionales se pueden observar directamente: son funciones de onda de valor real; las ondas ópticas y materiales no se pueden observar directamente: son funciones de onda de valor complejo. Algunas de las diferencias entre la interferencia de ondas de valor real y de valor complejo incluyen:

1. La interferencia involucra diferentes tipos de funciones matemáticas: una onda clásica es una función real que representa el desplazamiento desde una posición de equilibrio; una función de onda óptica o cuántica es una función compleja . Una onda clásica en cualquier punto puede ser positiva o negativa; la función de probabilidad cuántica no es negativa.
2. Dos ondas reales diferentes en el mismo medio pueden interferir; las ondas complejas deben ser coherentes para interferir. En la práctica, esto significa que la onda debe provenir de la misma fuente y tener frecuencias similares.
3. La interferencia de ondas reales se obtiene simplemente sumando los desplazamientos desde el equilibrio (o amplitudes) de las dos ondas; en la interferencia de ondas complejas, medimos el módulo de la función de onda al cuadrado.

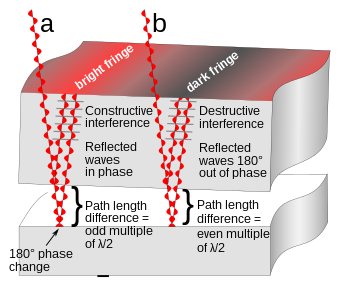
Como la frecuencia de las ondas de luz (~10 ¹⁴ Hz) es demasiado alta para que los detectores disponibles actualmente detecten la variación del campo eléctrico de la luz, es posible observar únicamente la intensidad de un patrón de interferencia óptica. La intensidad de la luz en un punto dado es proporcional al cuadrado de la amplitud media de la onda. Esto se puede expresar matemáticamente de la siguiente manera. El desplazamiento de las dos ondas en un punto r es:

$${\displaystyle U_{1}(\mathbf {r} ,t)=A_{1}(\mathbf {r} )e^{i[\varphi _{1}(\mathbf {r} )-\omega t]}}$$$${\displaystyle U_{2}(\mathbf {r} ,t)=A_{2}(\mathbf {r} )e^{i[\varphi _{2}(\mathbf {r} )-\omega t]}}$$

donde A representa la magnitud del desplazamiento, φ representa la fase y ω representa la frecuencia angular .

El desplazamiento de las ondas sumadas es

$${\displaystyle U(\mathbf {r} ,t)=A_{1}(\mathbf {r} )e^{i[\varphi _{1}(\mathbf {r} )-\omega t]}+A_{2}(\mathbf {r} )e^{i[\varphi _{2}(\mathbf {r} )-\omega t]}.}$$

La intensidad de la luz en r está dada por

$${\displaystyle I(\mathbf {r} )=\int U(\mathbf {r} ,t)U^{*}(\mathbf {r} ,t)\,dt\propto A_{1}^{2}(\mathbf {r} )+A_{2}^{2}(\mathbf {r} )+2A_{1}(\mathbf {r} )A_{2}(\mathbf {r} )\cos[\varphi _{1}(\mathbf {r} )-\varphi _{2}(\mathbf {r} )].}$$

Esto se puede expresar en términos de las intensidades de las ondas individuales como

$${\displaystyle I(\mathbf {r} )=I_{1}(\mathbf {r} )+I_{2}(\mathbf {r} )+2{\sqrt {I_{1}(\mathbf {r} )I_{2}(\mathbf {r} )}}\cos[\varphi _{1}(\mathbf {r} )-\varphi _{2}(\mathbf {r} )].}$$

De este modo, el patrón de interferencia representa la diferencia de fase entre las dos ondas, y los máximos se producen cuando la diferencia de fase es múltiplo de 2 π . Si los dos haces tienen la misma intensidad, los máximos son cuatro veces más brillantes que los haces individuales y los mínimos tienen una intensidad cero.

Clásicamente, las dos ondas deben tener la misma polarización para dar lugar a franjas de interferencia, ya que no es posible que ondas de polarizaciones diferentes se cancelen entre sí o se sumen. En cambio, cuando se suman ondas de polarización diferente, dan lugar a una onda de un estado de polarización diferente .

En el campo de la mecánica cuántica, las teorías de Paul Dirac y Richard Feynman ofrecen un enfoque más moderno. Dirac demostró que cada cuanto o fotón de luz actúa por sí mismo, lo que él mismo afirmó con su famosa frase "cada fotón interfiere consigo mismo". Richard Feynman demostró que al evaluar una integral de trayectorias en la que se consideran todas las trayectorias posibles, surgirá una serie de trayectorias con mayor probabilidad. En películas delgadas, por ejemplo, el espesor de la película que no es un múltiplo de la longitud de onda de la luz no permitirá que los cuantos la atraviesen, solo es posible la reflexión.

La discusión anterior supone que las ondas que interfieren entre sí son monocromáticas, es decir, tienen una sola frecuencia; esto requiere que sean infinitas en el tiempo. Sin embargo, esto no es ni práctico ni necesario. Dos ondas idénticas de duración finita cuya frecuencia es fija durante ese período darán lugar a un patrón de interferencia mientras se superponen. Dos ondas idénticas que consisten en un espectro estrecho de ondas de frecuencia de duración finita (pero más corta que su tiempo de coherencia), darán lugar a una serie de patrones de franjas con espaciamientos ligeramente diferentes y, siempre que la dispersión de espaciamientos sea significativamente menor que el espaciamiento de franjas promedio, se observará nuevamente un patrón de franjas durante el tiempo en que las dos ondas se superpongan.

Las fuentes de luz convencionales emiten ondas de diferentes frecuencias y en diferentes momentos desde distintos puntos de la fuente. Si la luz se divide en dos ondas y luego se vuelve a combinar, cada onda de luz individual puede generar un patrón de interferencia con su otra mitad, pero los patrones de franjas individuales generados tendrán diferentes fases y espaciamientos, y normalmente no será observable ningún patrón de franjas general. Sin embargo, las fuentes de luz de un solo elemento, como las lámparas de vapor de sodio o mercurio, tienen líneas de emisión con espectros de frecuencia bastante estrechos. Cuando se filtran espacialmente y por color, y luego se dividen en dos ondas, se pueden superponer para generar franjas de interferencia. ^[5] Toda la interferometría anterior a la invención del láser se realizó utilizando tales fuentes y tuvo una amplia gama de aplicaciones exitosas.

Un rayo láser generalmente se aproxima mucho más a una fuente monocromática y, por lo tanto, es mucho más sencillo generar franjas de interferencia utilizando un láser. La facilidad con la que se pueden observar las franjas de interferencia con un rayo láser a veces puede causar problemas, ya que las reflexiones dispersas pueden generar franjas de interferencia falsas que pueden generar errores.

Normalmente, en interferometría se utiliza un único haz láser, aunque se han observado interferencias utilizando dos láseres independientes cuyas frecuencias coincidían lo suficiente para satisfacer los requisitos de fase. ^[6] Esto también se ha observado en el caso de interferencias de campo amplio entre dos fuentes láser incoherentes. ^[7]

También es posible observar franjas de interferencia utilizando luz blanca. Se puede considerar que un patrón de franjas de luz blanca está formado por un «espectro» de patrones de franjas, cada uno de ellos con un espaciado ligeramente diferente. Si todos los patrones de franjas están en fase en el centro, entonces las franjas aumentarán de tamaño a medida que disminuya la longitud de onda y la intensidad sumada mostrará tres o cuatro franjas de color variable. Young describe esto de forma muy elegante en su análisis de la interferencia de dos rendijas. Dado que las franjas de luz blanca se obtienen solo cuando las dos ondas han recorrido distancias iguales desde la fuente de luz, pueden ser muy útiles en interferometría, ya que permiten identificar la franja de diferencia de trayectoria cero. ^[8]

Para generar franjas de interferencia, la luz de la fuente debe dividirse en dos ondas que luego deben volver a combinarse. Tradicionalmente, los interferómetros se han clasificado como sistemas de división de amplitud o de división de frente de onda.

En un sistema de división de amplitud, se utiliza un divisor de haz para dividir la luz en dos haces que viajan en direcciones diferentes y que luego se superponen para producir el patrón de interferencia. El interferómetro de Michelson y el interferómetro de Mach-Zehnder son ejemplos de sistemas de división de amplitud.

En los sistemas de división de frente de onda, la onda se divide en el espacio; algunos ejemplos son el interferómetro de doble rendija de Young y el espejo de Lloyd .

La interferencia también se puede observar en fenómenos cotidianos como la iridiscencia y la coloración estructural . Por ejemplo, los colores que se ven en una burbuja de jabón surgen de la interferencia de la luz que se refleja en las superficies delantera y trasera de la fina película de jabón. Dependiendo del espesor de la película, diferentes colores interfieren de manera constructiva y destructiva.

• Iridiscencia causada por interferencia de película delgada
• 
  Teléfono inteligente con panel posterior iridiscente
• 
  Un derrame de petróleo
• 
  Interferencia de luz blanca en una burbuja de jabón.

Part of a series of articles about
Quantum mechanics
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ Schrödinger equation
Introduction Glossary History
Background Classical mechanics Old quantum theory Bra–ket notation Hamiltonian Interference
Fundamentals Complementarity Decoherence Entanglement Energy level Measurement Nonlocality Quantum number State Superposition Symmetry Tunnelling Uncertainty Wave function Collapse
Experiments Bell's inequality CHSH inequality Davisson–Germer Double-slit Elitzur–Vaidman Franck–Hertz Leggett inequality Leggett–Garg inequality Mach–Zehnder Popper Quantum eraser Delayed-choice Schrödinger's cat Stern–Gerlach Wheeler's delayed-choice
Formulations Overview Heisenberg Interaction Matrix Phase-space Schrödinger Sum-over-histories (path integral)
Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Local Superdeterminism Many-worlds Objective-collapse Quantum logic Relational Transactional Von Neumann–Wigner
Advanced topics Relativistic quantum mechanics Quantum field theory Quantum information science Quantum computing Quantum chaos EPR paradox Density matrix Scattering theory Quantum statistical mechanics Quantum machine learning
Scientists Aharonov Bell Bethe Blackett Bloch Bohm Bohr Born Bose de Broglie Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Lamb Landau Laue Moseley Millikan Onnes Pauli Planck Rabi Raman Rydberg Schrödinger Simmons Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

La interferencia cuántica –el comportamiento ondulatorio observado de la materia ^[9] – se parece a la interferencia óptica. Sea una solución de función de onda de la ecuación de Schrödinger para un objeto mecánico cuántico. Entonces, la probabilidad de observar el objeto en la posición es donde * indica conjugación compleja . La interferencia cuántica se refiere a la cuestión de esta probabilidad cuando la función de onda se expresa como una suma o superposición lineal de dos términos :${\displaystyle \Psi (x,t)}$ ${\displaystyle P(x)}$${\displaystyle x}$${\displaystyle P(x)=|\Psi (x,t)|^{2}=\Psi ^{*}(x,t)\Psi (x,t)}$${\displaystyle \Psi (x,t)=\Psi _{A}(x,t)+\Psi _{B}(x,t)}$$${\displaystyle P(x)=|\Psi (x,t)|^{2}=|\Psi _{A}(x,t)|^{2}+|\Psi _{B}(x,t)|^{2}+(\Psi _{A}^{*}(x,t)\Psi _{B}(x,t)+\Psi _{A}(x,t)\Psi _{B}^{*}(x,t))}$$

Por lo general, y corresponden a situaciones distintas A y B. Cuando este es el caso, la ecuación indica que el objeto puede estar en la situación A o en la situación B. La ecuación anterior puede interpretarse entonces como: La probabilidad de encontrar el objeto en es la probabilidad de encontrar el objeto en cuando está en la situación A más la probabilidad de encontrar el objeto en cuando está en la situación B más un término extra. Este término extra, que se llama término de interferencia cuántica , está en la ecuación anterior. Como en el caso de la onda clásica anterior, el término de interferencia cuántica puede agregar (interferencia constructiva) o restar (interferencia destructiva) de en la ecuación anterior dependiendo de si el término de interferencia cuántica es positivo o negativo. Si este término está ausente para todos , entonces no hay interferencia mecánica cuántica asociada con las situaciones A y B.${\displaystyle \Psi _{A}(x,t)}$${\displaystyle \Psi _{B}(x,t)}$${\displaystyle \Psi (x,t)=\Psi _{A}(x,t)+\Psi _{B}(x,t)}$${\displaystyle x}$${\displaystyle x}$${\displaystyle x}$${\displaystyle \Psi _{A}^{*}(x,t)\Psi _{B}(x,t)+\Psi _{A}(x,t)\Psi _{B}^{*}(x,t)}$${\displaystyle |\Psi _{A}(x,t)|^{2}+|\Psi _{B}(x,t)|^{2}}$${\displaystyle x}$

El ejemplo más conocido de interferencia cuántica es el experimento de la doble rendija . En este experimento, las ondas de materia de electrones, átomos o moléculas se aproximan a una barrera con dos rendijas. Una rendija se convierte en y la otra se convierte en . El patrón de interferencia se produce en el lado lejano, observado por detectores adecuados a las partículas que originan la onda de materia . ^[10] El patrón coincide con el patrón óptico de doble rendija.${\displaystyle \Psi _{A}(x,t)}$${\displaystyle \Psi _{B}(x,t)}$

En acústica , un pulso es un patrón de interferencia entre dos sonidos de frecuencias ligeramente diferentes , percibido como una variación periódica en el volumen cuya tasa es la diferencia de las dos frecuencias.

Con instrumentos de afinación que pueden producir tonos sostenidos, los pulsos se pueden reconocer fácilmente. Afinar dos tonos al unísono presentará un efecto peculiar: cuando los dos tonos son cercanos en tono pero no idénticos, la diferencia en frecuencia genera el pulso. El volumen varía como en un trémolo a medida que los sonidos interfieren alternativamente de manera constructiva y destructiva. A medida que los dos tonos se acercan gradualmente al unísono, el pulso se ralentiza y puede volverse tan lento que sea imperceptible. A medida que los dos tonos se alejan, su frecuencia de pulso comienza a acercarse al rango de la percepción del tono humano, ^[11] el pulso comienza a sonar como una nota y se produce un tono de combinación . Este tono de combinación también puede denominarse fundamental faltante , ya que la frecuencia de pulso de dos tonos cualesquiera es equivalente a la frecuencia de su frecuencia fundamental implícita.

La interferometría ha jugado un papel importante en el avance de la física y también tiene una amplia gama de aplicaciones en la medición física y de ingeniería.

El interferómetro de doble rendija de Thomas Young, en 1803, demostró la existencia de franjas de interferencia cuando dos pequeños agujeros eran iluminados por la luz procedente de otro pequeño agujero que estaba iluminado por la luz solar. Young fue capaz de estimar la longitud de onda de diferentes colores en el espectro a partir del espaciamiento de las franjas. El experimento jugó un papel importante en la aceptación general de la teoría ondulatoria de la luz. ^[8] En mecánica cuántica, se considera que este experimento demuestra la inseparabilidad de las naturalezas ondulatoria y corpuscular de la luz y otras partículas cuánticas ( dualidad onda-partícula ). A Richard Feynman le gustaba decir que toda la mecánica cuántica se puede extraer de una reflexión cuidadosa sobre las implicaciones de este único experimento. ^[12]

Los resultados del experimento de Michelson-Morley se consideran generalmente como la primera evidencia sólida contra la teoría de un éter luminífero y a favor de la relatividad especial .

La interferometría se ha utilizado para definir y calibrar patrones de longitud . Cuando el metro se definió como la distancia entre dos marcas en una barra de platino-iridio, Michelson y Benoît utilizaron la interferometría para medir la longitud de onda de la línea roja de cadmio en el nuevo patrón, y también demostraron que podía usarse como patrón de longitud. Sesenta años después, en 1960, el metro en el nuevo sistema SI se definió como igual a 1.650.763,73 longitudes de onda de la línea de emisión naranja-roja en el espectro electromagnético del átomo de kriptón-86 en el vacío. Esta definición fue reemplazada en 1983 por la definición del metro como la distancia recorrida por la luz en el vacío durante un intervalo de tiempo específico. La interferometría sigue siendo fundamental para establecer la cadena de calibración en la medición de longitud.

La interferometría se utiliza en la calibración de calibres de deslizamiento (llamados bloques patrón en los EE. UU.) y en máquinas de medición de coordenadas . También se utiliza en la prueba de componentes ópticos. ^[13]

En 1946 se desarrolló una técnica llamada interferometría astronómica . Los radiointerferómetros astronómicos suelen constar de conjuntos de antenas parabólicas o conjuntos bidimensionales de antenas omnidireccionales. Todos los telescopios del conjunto están muy separados y suelen estar conectados entre sí mediante cable coaxial , guía de ondas , fibra óptica u otro tipo de línea de transmisión . La interferometría aumenta la señal total recogida, pero su objetivo principal es aumentar enormemente la resolución mediante un proceso llamado síntesis de apertura . Esta técnica funciona superponiendo (interfiriendo) las ondas de señal de los diferentes telescopios según el principio de que las ondas que coinciden con la misma fase se sumarán entre sí, mientras que dos ondas que tienen fases opuestas se cancelarán entre sí. Esto crea un telescopio combinado que es equivalente en resolución (aunque no en sensibilidad) a una sola antena cuyo diámetro es igual al espaciamiento de las antenas más alejadas en el conjunto.

Un interferómetro acústico es un instrumento que mide las características físicas de las ondas sonoras en un gas o líquido, como la velocidad , la longitud de onda, la absorción o la impedancia . Un cristal vibrante crea ondas ultrasónicas que se irradian al medio. Las ondas inciden en un reflector colocado en paralelo al cristal, se reflejan de nuevo en la fuente y se miden.

Busque interferencia en Wikcionario, el diccionario libre.

Wikimedia Commons tiene medios relacionados con Interferencia.

• Modelo de simulación de interferencia de ondas unidimensionales en JavaScript
• Expresiones de posición y espaciamiento de franjas
• Simulación en Java de la interferencia de ondas de agua 1
• Simulación en Java de la interferencia de ondas de agua 2
• Animaciones Flash que muestran interferencias Archivado el 24 de junio de 2009 en Wayback Machine.