Toro

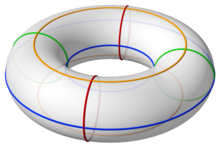
En geometría , un toro ( pl.: toros o toros ) es una superficie de revolución generada al girar un círculo en el espacio tridimensional una revolución completa alrededor de un eje que es coplanar con el círculo. Los principales tipos de toros incluyen toros de anillo, toros de cuerno y toros de huso. A un toro de anillo a veces se lo conoce coloquialmente como rosquilla o donut .

Si el eje de revolución no toca el círculo, la superficie tiene forma de anillo y se llama toro de revolución , también conocido como toro anular . Si el eje de revolución es tangente al círculo, la superficie es un toro de cuerno . Si el eje de revolución pasa dos veces por el círculo, la superficie es un toro de huso (o toro autocruzado o toro autointersecante ). Si el eje de revolución pasa por el centro del círculo, la superficie es un toro degenerado, una esfera de doble cubierta . Si la curva girada no es un círculo, la superficie se llama toroide , como en un toroide cuadrado.

Los objetos del mundo real que se aproximan a un toro de revolución incluyen anillos de natación , cámaras de aire y anillos de ringette .

Un toro no debe confundirse con un toro sólido , que se forma al girar un disco , en lugar de un círculo, alrededor de un eje. Un toro sólido es un toro más el volumen dentro del toro. Los objetos del mundo real que se aproximan a un toro sólido incluyen juntas tóricas , aros salvavidas no inflables , donas con forma de anillo y bagels .

En topología , un toro anular es homeomorfo al producto cartesiano de dos círculos : , y este último se toma como la definición en ese contexto. Es una 2-variedad compacta de género 1. El toro anular es una forma de incrustar este espacio en el espacio euclidiano , pero otra forma de hacerlo es el producto cartesiano de la incrustación de en el plano consigo mismo. Esto produce un objeto geométrico llamado toro de Clifford , una superficie en el 4-espacio .${\displaystyle S^{1}\times S^{1}}$$Estilo de visualización S1$

En el campo de la topología , un toro es cualquier espacio topológico que es homeomorfo a un toro. ^[1] La superficie de una taza de café y una dona son ambos toros topológicos con género uno.

Un ejemplo de toro se puede construir tomando una tira rectangular de material flexible, como caucho, y uniendo el borde superior con el borde inferior y el borde izquierdo con el borde derecho, sin ninguna media torsión (compárese con la botella de Klein ).

Torus es una palabra latina que significa "redondo, hinchazón, elevación, protuberancia".

Un toro se puede parametrizar como: ^[2]$${\displaystyle {\begin{aligned}x(\theta ,\varphi )&=(R+r\cos \theta )\cos {\varphi }\\y(\theta ,\varphi )&=(R+r \cos \theta )\sin {\varphi }\\z(\theta ,\varphi )&=r\sin \theta \\\end{alineado}}}$$

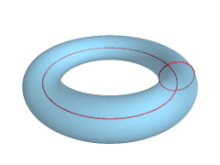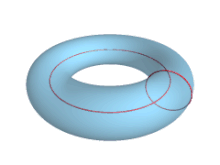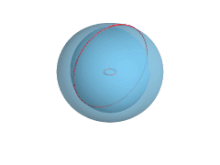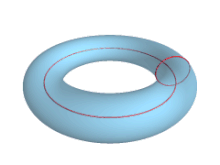
utilizando coordenadas angulares que representan la rotación alrededor del tubo y la rotación alrededor del eje de revolución del toro, respectivamente, donde el radio mayor es la distancia desde el centro del tubo hasta el centro del toro y el radio menor es el radio del tubo. ^[3]${\displaystyle \theta ,\varphi \en [0,2\pi ),}$ ${\estilo de visualización R}$ ${\estilo de visualización r}$

La relación se denomina relación de aspecto del toro. El típico dulce tipo donut tiene una relación de aspecto de aproximadamente 3 a 2.${\estilo de visualización R/r}$

Una ecuación implícita en coordenadas cartesianas para un toro radialmente simétrico respecto del eje - es${\estilo de visualización z}$$${\displaystyle {\textstyle {\bigl (}{\sqrt {x^{2}+y^{2}}}-R{\bigr )}^{2}}+z^{2}=r^{2}.}$$

Al eliminar algebraicamente la raíz cuadrada se obtiene una ecuación cuártica ,$${\displaystyle \left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\left(x^{2}+y^{2}\right).}$$

Las tres clases de toros estándar corresponden a las tres posibles relaciones de aspecto entre R y r :

• Cuando R > r , la superficie será el conocido toro anular o anillo de anclaje.
• R = r corresponde al toro del cuerno, que en efecto es un toro sin "agujero".
• R < r describe el toro del huso autointersecante; su capa interior es un limón y su capa exterior es una manzana .
• Cuando R = 0 , el toro degenera al radio de la esfera r .
• Cuando r = 0 , el toro degenera al radio del círculo R.

Cuando R ≥ r , el interior de este toro es difeomorfo (y, por lo tanto, homeomorfo) a un producto de un disco abierto euclidiano y un círculo. El volumen de este toro sólido y el área de superficie de su toro se calculan fácilmente utilizando el teorema del centroide de Pappus , dando: ^[4]$${\displaystyle {\textstyle {\bigl (}{\sqrt {x^{2}+y^{2}}}-R{\bigr )}^{2}}+z^{2}<r^{2}}$$$${\displaystyle {\begin{aligned}A&=\left(2\pi r\right)\left(2\pi R\right)=4\pi ^{2}Rr,\\[5mu]V&=\left(\pi r^{2}\right)\left(2\pi R\right)=2\pi ^{2}Rr^{2}.\end{aligned}}}$$

Estas fórmulas son las mismas que para un cilindro de longitud 2π R y radio r , obtenido al cortar el tubo a lo largo del plano de un pequeño círculo y desenrollarlo enderezando (rectificando) la línea que corre alrededor del centro del tubo. Las pérdidas de superficie y volumen en el lado interior del tubo anulan exactamente las ganancias en el lado exterior.

Expresando el área de la superficie y el volumen por la distancia p de un punto más externo de la superficie del toro al centro, y la distancia q de un punto más interno al centro (de modo que R = ⁠p + q/2⁠ y r = ⁠p - q/2⁠ ), produce$${\displaystyle {\begin{aligned}A&=4\pi ^{2}\left({\frac {p+q}{2}}\right)\left({\frac {p-q}{2}}\right)=\pi ^{2}(p+q)(p-q),\\[5mu]V&=2\pi ^{2}\left({\frac {p+q}{2}}\right)\left({\frac {p-q}{2}}\right)^{2}={\tfrac {1}{4}}\pi ^{2}(p+q)(p-q)^{2}.\end{aligned}}}$$

Como un toro es el producto de dos círculos, a veces se utiliza una versión modificada del sistema de coordenadas esféricas . En las coordenadas esféricas tradicionales hay tres medidas: R , la distancia desde el centro del sistema de coordenadas, y θ y φ , ángulos medidos desde el punto central.

Como un toro tiene, efectivamente, dos puntos centrales, los puntos centrales de los ángulos se desplazan; φ mide el mismo ángulo que en el sistema esférico, pero se conoce como dirección "toroidal". El punto central de θ se desplaza al centro de r y se conoce como dirección "poloidal". Estos términos se utilizaron por primera vez en una discusión sobre el campo magnético de la Tierra, donde "poloidal" se utilizó para denotar "la dirección hacia los polos". ^[5]

En el uso moderno, los términos toroidal y poloidal se utilizan más comúnmente para referirse a los dispositivos de fusión por confinamiento magnético .

This section includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this section by introducing more precise citations. (November 2015) (Learn how and when to remove this message)

Topológicamente , un toro es una superficie cerrada definida como el producto de dos círculos : S ¹  ×  S ¹ . Esto puede verse como si se encontrara en C ² y es un subconjunto de la 3-esfera S ³ de radio √2. Este toro topológico también se denomina a menudo toro de Clifford . ^[6] De hecho, S ³ se completa con una familia de toros anidados de esta manera (con dos círculos degenerados), un hecho que es importante en el estudio de S ³ como un haz de fibras sobre S ² (el haz de Hopf ).

La superficie descrita anteriormente, dada la topología relativa de , es homeomorfa a un toro topológico siempre que no intersecte su propio eje. Un homeomorfismo particular se da al proyectar estereográficamente el toro topológico hacia desde el polo norte de S ³ . ${\displaystyle \mathbb {R} ^{3}}$${\displaystyle \mathbb {R} ^{3}}$

El toro también puede describirse como un cociente del plano cartesiano bajo las identificaciones

${\displaystyle (x,y)\sim (x+1,y)\sim (x,y+1),\,}$

o, equivalentemente, como el cociente del cuadrado unitario al pegar los bordes opuestos, descrito como un polígono fundamental ABA ⁻¹ B ⁻¹ .

El grupo fundamental del toro no es más que el producto directo del grupo fundamental del círculo consigo mismo:

${\displaystyle \pi _{1}(\mathbb {T} ^{2})=\pi _{1}(\mathbb {S} ^{1})\times \pi _{1}(\mathbb {S} ^{1})\cong \mathbb {Z} \times \mathbb {Z} .}$^[7]

Intuitivamente hablando, esto significa que una trayectoria cerrada que rodea el "agujero" del toro (por ejemplo, un círculo que traza una latitud particular) y luego rodea el "cuerpo" del toro (por ejemplo, un círculo que traza una longitud particular) se puede deformar en una trayectoria que rodea el cuerpo y luego el agujero. Por lo tanto, las trayectorias estrictamente "latitudinales" y estrictamente "longitudinales" se conmutan. Una afirmación equivalente puede imaginarse como dos cordones de zapatos que pasan uno a través del otro, luego se desenrollan y luego se reenrollan.

Si se perfora un toro y se le da la vuelta, se obtiene otro toro con las líneas de latitud y longitud intercambiadas. Esto equivale a construir un toro a partir de un cilindro, uniendo los extremos circulares de dos maneras: alrededor del exterior, como si se unieran dos extremos de una manguera de jardín, o a través del interior, como si se enrollara un calcetín (al que se le corta la punta). Además, si el cilindro se hizo pegando dos lados opuestos de un rectángulo, elegir los otros dos lados provocará la misma inversión de orientación.

El primer grupo de homología del toro es isomorfo al grupo fundamental (esto se deduce del teorema de Hurewicz ya que el grupo fundamental es abeliano ).

El 2-toro cubre dos veces la 2-esfera, con cuatro puntos de ramificación . Cada estructura conforme en el 2-toro se puede representar como una cubierta de dos láminas de la 2-esfera. Los puntos en el toro que corresponden a los puntos de ramificación son los puntos de Weierstrass . De hecho, el tipo conforme del toro está determinado por la relación cruzada de los cuatro puntos.

El toro tiene una generalización a dimensiones superiores, laToro n-dimensional , a menudo llamado n -toroohipertoropara abreviar. (Este es el significado más típico del término "n-toro", el otro se refiere anagujeros o de géneron.^[8]) Recordando que el toro es el espacio producto de dos círculos, eln-dimensional es el producto dencírculos. Es decir:

${\displaystyle \mathbb {T} ^{n}=\underbrace {\mathbb {S} ^{1}\times \cdots \times \mathbb {S} ^{1}} _{n}.}$

El 1-toro estándar es simplemente el círculo: . El toro analizado anteriormente es el 2-toro estándar, . Y de manera similar al 2-toro, el n -toro, puede describirse como un cociente de desplazamientos subintegrales en cualquier coordenada. Es decir, el n -toro es módulo la acción de la red entera (con la acción tomada como suma vectorial). De manera equivalente, el n -toro se obtiene a partir del hipercubo n -dimensional pegando las caras opuestas.${\displaystyle \mathbb {T} ^{1}=\mathbb {S} ^{1}}$${\displaystyle \mathbb {T} ^{2}}$${\displaystyle \mathbb {T} ^{n}}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {Z} ^{n}}$

Un n -toro en este sentido es un ejemplo de una variedad compacta de n dimensiones . También es un ejemplo de un grupo de Lie abeliano compacto . Esto se deduce del hecho de que el círculo unitario es un grupo de Lie abeliano compacto (cuando se identifica con los números complejos unitarios con multiplicación). La multiplicación de grupos en el toro se define entonces mediante la multiplicación por coordenadas.

Los grupos toroidales desempeñan un papel importante en la teoría de los grupos de Lie compactos . Esto se debe en parte al hecho de que en cualquier grupo de Lie compacto G siempre se puede encontrar un toro máximo ; es decir, un subgrupo cerrado que es un toro de la mayor dimensión posible. Dichos toros máximos T tienen un papel de control en la teoría de G conexos . Los grupos toroidales son ejemplos de protoros , que (como los toros) son grupos abelianos compactos conexos, que no necesitan ser variedades .

Los automorfismos de T se construyen fácilmente a partir de automorfismos de la red , que se clasifican por matrices integrales invertibles de tamaño n con una inversa integral; éstas son justamente las matrices integrales con determinante ±1. Haciéndolas actuar de la manera habitual, se tiene el típico automorfismo toral en el cociente.${\displaystyle \mathbb {Z} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

El grupo fundamental de un n -toro es un grupo abeliano libre de rango n . El k -ésimo grupo de homología de un n -toro es un grupo abeliano libre de rango n choose k . De ello se deduce que la característica de Euler del n -toro es 0 para todo n . El anillo de cohomología H • ( , Z ) puede identificarse con el álgebra exterior sobre el módulo Z ^cuyos generadores son  los duales de los n ciclos no triviales .${\displaystyle \mathbb {T} ^{n}}$ ${\displaystyle \mathbb {Z} ^{n}}$

Como el n -toro es el producto n -fold del círculo, el n -toro es el espacio de configuración de n puntos ordenados, no necesariamente distintos, en el círculo. Simbólicamente, . El espacio de configuración de puntos no ordenados , no necesariamente distintos, es en consecuencia el orbifold , que es el cociente del toro por el grupo simétrico en n letras (permutando las coordenadas).${\displaystyle \mathbb {T} ^{n}=(\mathbb {S} ^{1})^{n}}$ ${\displaystyle \mathbb {T} ^{n}/\mathbb {S} _{n}}$

Para n = 2, el cociente es la banda de Möbius , cuya arista corresponde a los puntos del orbifold donde coinciden las dos coordenadas. Para n = 3, este cociente puede describirse como un toro sólido con sección transversal de triángulo equilátero , con un giro ; equivalentemente, como un prisma triangular cuyas caras superior e inferior están conectadas con un giro de 1/3 (120°): el interior tridimensional corresponde a los puntos del 3-toro donde las 3 coordenadas son distintas, la cara bidimensional corresponde a los puntos con 2 coordenadas iguales y la 3.ª diferente, mientras que la arista unidimensional corresponde a los puntos con las 3 coordenadas idénticas.

Estos orbifolds han encontrado aplicaciones significativas para la teoría musical en el trabajo de Dmitri Tymoczko y colaboradores (Felipe Posada, Michael Kolinas, et al.), siendo utilizados para modelar tríadas musicales . ^{[9] [10]}

Un toro plano es un toro con la métrica heredada de su representación como el cociente , / L , donde L es un subgrupo discreto de isomorfo a . Esto le da al cociente la estructura de una variedad de Riemann , así como la estructura de un grupo de Lie abeliano. Quizás el ejemplo más simple de esto es cuando L = : , que también puede describirse como el plano cartesiano bajo las identificaciones ( x , y ) ~ ( x + 1, y ) ~ ( x , y + 1) . Este toro plano en particular (y cualquier versión de escala uniforme del mismo) se conoce como el toro plano "cuadrado".${\displaystyle \mathbb {R} ^{2}}$${\displaystyle \mathbb {R} ^{2}}$${\displaystyle \mathbb {Z} ^{2}}$${\displaystyle \mathbb {Z} ^{2}}$${\displaystyle \mathbb {R} ^{2}/\mathbb {Z} ^{2}}$

Esta métrica del toro plano cuadrado también se puede realizar mediante incrustaciones específicas del conocido 2-toro en el espacio euclidiano de 4 dimensiones o dimensiones superiores. Su superficie tiene curvatura gaussiana cero en todas partes. Es plana en el mismo sentido que la superficie de un cilindro es plana. En 3 dimensiones, se puede doblar una hoja de papel plana para formar un cilindro sin estirar el papel, pero este cilindro no se puede doblar para formar un toro sin estirar el papel (a menos que se abandonen algunas condiciones de regularidad y diferenciabilidad, véase más adelante).

Una incrustación euclidiana simple de 4 dimensiones de un toro plano rectangular (más general que el cuadrado) es la siguiente:

${\displaystyle (x,y,z,w)=(R\cos u,R\sin u,P\cos v,P\sin v)}$

donde R y P son constantes positivas que determinan la relación de aspecto. Es difeomórfico a un toro regular pero no isométrico . No se puede incrustar analíticamente ( suave de clase C ^k , 2 ≤ k ≤ ∞ ) en el 3-espacio euclidiano. Para mapearlo en el 3 -espacio es necesario estirarlo, en cuyo caso parece un toro regular. Por ejemplo, en el siguiente mapa:

${\displaystyle (x,y,z)=((R+P\sin v)\cos u,(R+P\sin v)\sin u,P\cos v).}$

Si R y P en la parametrización del toro plano anterior forman un vector unitario ( R , P ) = (cos( ​​η ), sen( η )) entonces u , v y 0 < η < π /2 parametrizan la 3-esfera unitaria como coordenadas de Hopf . En particular, para ciertas elecciones muy específicas de un toro plano cuadrado en la 3-esfera S ³ , donde η = π /4 anterior, el toro dividirá la 3-esfera en dos subconjuntos de toros sólidos congruentes con la superficie del toro plano antes mencionada como su límite común . Un ejemplo es el toro T definido por

${\displaystyle T=\left\{(x,y,z,w)\in \mathbb {S} ^{3}\mid x^{2}+y^{2}={\frac {1}{2}},\ z^{2}+w^{2}={\frac {1}{2}}\right\}.}$

Otros toros en S ³ que tienen esta propiedad de partición incluyen los toros cuadrados de la forma Q ⋅ T , donde Q es una rotación del espacio de 4 dimensiones , o en otras palabras Q es un miembro del grupo de Lie SO(4).${\displaystyle \mathbb {R} ^{4}}$

Se sabe que no existe ninguna incrustación C ² (dos veces continuamente diferenciable) de un toro plano en el espacio tridimensional. (La idea de la prueba es tomar una esfera grande que contenga dicho toro plano en su interior y encoger el radio de la esfera hasta que toque el toro por primera vez. Tal punto de contacto debe ser una tangencia. Pero eso implicaría que parte del toro, dado que tiene curvatura cero en todas partes, debe quedar estrictamente fuera de la esfera, lo cual es una contradicción). Por otro lado, según el teorema de Nash-Kuiper , que se demostró en la década de 1950, existe una incrustación isométrica C ^1. Esta es únicamente una prueba de existencia y no proporciona ecuaciones explícitas para tal incrustación.

En abril de 2012, se encontró una incrustación explícita C ¹ (continuamente diferenciable) de un toro plano en un espacio euclidiano tridimensional . ^{[11] [12] [13] [14]} Es un toro plano en el sentido de que, como espacio métrico, es isométrico a un toro cuadrado plano. Es similar en estructura a un fractal , ya que se construye corrugando repetidamente un toro ordinario. Al igual que los fractales, no tiene una curvatura gaussiana definida. Sin embargo, a diferencia de los fractales, tiene normales de superficie definidas , lo que produce un llamado "fractal suave". La clave para obtener la suavidad de este toro corrugado es hacer que las amplitudes de las corrugaciones sucesivas disminuyan más rápido que sus "longitudes de onda". ^[15] (Estas corrugaciones infinitamente recursivas se utilizan únicamente para incrustaciones en tres dimensiones; no son una característica intrínseca del toro plano). Esta es la primera vez que una incrustación de este tipo se define mediante ecuaciones explícitas o se representa mediante gráficos de computadora.${\displaystyle \mathbb {R} ^{3}}$

En el estudio de las superficies de Riemann , se dice que dos superficies geométricas compactas y lisas son "conformemente equivalentes" cuando existe un homeomorfismo suave entre ellas que preserva tanto el ángulo como la orientación. El teorema de uniformización garantiza que toda superficie de Riemann es conformemente equivalente a una que tiene una curvatura gaussiana constante . En el caso de un toro, la curvatura constante debe ser cero. Luego se define el " espacio de módulos " del toro para que contenga un punto para cada clase de equivalencia conforme, con la topología apropiada. Resulta que este espacio de módulos M puede identificarse con una esfera perforada que es lisa excepto por dos puntos que tienen un ángulo menor que 2π (radianes) alrededor de ellos: uno tiene un ángulo total = π y el otro tiene un ángulo total = 2π/3.

M puede convertirse en un espacio compacto M* añadiendo un punto adicional que represente el caso límite a medida que un toro rectangular se acerca a una relación de aspecto de 0 en el límite. El resultado es que este espacio de módulos compactificado es una esfera con tres puntos que tienen cada uno un ángulo total menor a 2π a su alrededor. (Estos puntos se denominan "cúspides"). Este punto adicional tendrá un ángulo total cero a su alrededor. Debido a la simetría, M* puede construirse pegando dos triángulos geodésicos congruentes en el plano hiperbólico a lo largo de sus límites (idénticos), donde cada triángulo tiene ángulos de π/2, π/3 y 0. Como resultado, el área de cada triángulo puede calcularse como π - (π/2 + π/3 + 0) = π/6, por lo que se deduce que el espacio de módulos compactificado M* tiene un área igual a π/3.

Las otras dos cúspides se encuentran en los puntos correspondientes en M* a) el toro cuadrado (ángulo total = π) y b) el toro hexagonal (ángulo total = 2π/3). Éstas son las únicas clases de equivalencia conforme de toros planos que tienen algún automorfismo conforme además de los generados por traslaciones y negaciones.

En la teoría de superficies existe una familia más general de objetos, las superficies de " género " g . Una superficie de género g es la suma conexa de g dos toros. (Y por lo tanto, el toro mismo es la superficie de género 1). Para formar una suma conexa de dos superficies, retira de cada una de ellas el interior de un disco y "pega" las superficies a lo largo de los círculos límite. (Es decir, fusiona los dos círculos límite para que se conviertan en un solo círculo). Para formar la suma conexa de más de dos superficies, toma sucesivamente la suma conexa de dos de ellas a la vez hasta que todas estén conexas. En este sentido, una superficie de género g se asemeja a la superficie de g donuts pegados uno al lado del otro, o a una 2-esfera con g asas adheridas.

Como ejemplos, una superficie de género cero (sin límite) es la biesfera , mientras que una superficie de género uno (sin límite) es el toro ordinario. Las superficies de género superior se denominan a veces toros con n agujeros (o, en raras ocasiones, toros con n pliegues). También se utilizan ocasionalmente los términos toro doble y toro triple .

El teorema de clasificación de superficies establece que toda superficie compacta conexa es topológicamente equivalente a la esfera o a la suma conexa de un cierto número de toros, discos y planos proyectivos reales .

género dos

género tres

Los poliedros con el tipo topológico de un toro se denominan poliedros toroidales y tienen la característica de Euler V − E + F = 0. Para cualquier número de agujeros, la fórmula se generaliza a V − E + F = 2 − 2 N , donde N es el número de agujeros.

El término "poliedro toroidal" también se utiliza para poliedros de género superior y para inmersiones de poliedros toroidales.

This section needs expansion. You can help by adding to it. (April 2010)

El grupo de homeomorfismos (o subgrupo de difeomorfismos) del toro se estudia en topología geométrica . Su grupo de clases de aplicación (los componentes conexos del grupo de homeomorfismos) es sobreyectivo sobre el grupo de matrices enteras invertibles, que pueden realizarse como aplicaciones lineales sobre el espacio de recubrimiento universal que conservan la red estándar (esto corresponde a los coeficientes enteros) y, por lo tanto, descienden al cociente.${\displaystyle \operatorname {GL} (n,\mathbb {Z} )}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \mathbb {Z} ^{n}}$

A nivel de homotopía y homología , el grupo de clases de mapeo puede identificarse como la acción sobre la primera homología (o equivalentemente, la primera cohomología, o sobre el grupo fundamental , ya que todos estos son naturalmente isomorfos; además, el primer grupo de cohomología genera el álgebra de cohomología :

${\displaystyle \operatorname {MCG} _{\operatorname {Ho} }(\mathbb {T} ^{n})=\operatorname {Aut} (\pi _{1}(X))=\operatorname {Aut} (\mathbb {Z} ^{n})=\operatorname {GL} (n,\mathbb {Z} ).}$

Dado que el toro es un espacio de Eilenberg-MacLane K ( G , 1), sus equivalencias de homotopía, hasta la homotopía, pueden identificarse con automorfismos del grupo fundamental); todas las equivalencias de homotopía del toro pueden realizarse mediante homeomorfismos – cada equivalencia de homotopía es homotópica a un homeomorfismo.

De esta manera, la secuencia corta y exacta del grupo de clases de mapeo se divide (una identificación del toro como el cociente de da una división, a través de los mapas lineales, como se muestra arriba):${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle 1\to \operatorname {Homeo} _{0}(\mathbb {T} ^{n})\to \operatorname {Homeo} (\mathbb {T} ^{n})\to \operatorname {MCG} _{\operatorname {TOP} }(\mathbb {T} ^{n})\to 1.}$

El grupo de clases de mapeo de superficies de géneros superiores es mucho más complicado y es un área de investigación activa.

El número de Heawood del toro es siete, lo que significa que cada gráfico que se puede incrustar en el toro tiene un número cromático de siete como máximo. (Dado que el gráfico completo se puede incrustar en el toro, y , el límite superior es estricto). De manera equivalente, en un toro dividido en regiones, siempre es posible colorear las regiones utilizando no más de siete colores de modo que ninguna región vecina sea del mismo color. (Contraste con el teorema de los cuatro colores para el plano ).${\displaystyle {\mathsf {K_{7}}}}$${\displaystyle \chi ({\mathsf {K_{7}}})=7}$

En matemáticas combinatorias , un toro de De Bruijn es una matriz de símbolos de un alfabeto (a menudo, solo 0 y 1) que contiene cada matriz de m por n exactamente una vez. Es un toro porque se considera que las aristas son envolventes para el propósito de encontrar matrices. Su nombre proviene de la secuencia de De Bruijn , que puede considerarse un caso especial donde n es 1 (una dimensión).

Un toro de revolución sólido puede ser cortado por n (> 0) planos como máximo

${\displaystyle {\begin{pmatrix}n+2\\n-1\end{pmatrix}}+{\begin{pmatrix}n\\n-1\end{pmatrix}}={\tfrac {1}{6}}(n^{3}+3n^{2}+8n)}$

partes. ^[16] (Esto supone que las piezas no pueden reorganizarse sino que deben permanecer en su lugar para todos los cortes).

Los primeros 11 números de partes, para 0 ≤ n ≤ 10 (incluido el caso de n = 0, no cubierto por las fórmulas anteriores), son los siguientes:

1, 2, 6, 13, 24, 40, 62, 91, 128, 174, 230, ... (secuencia A003600 en la OEIS ).

• Nociones de Geometría Analítica y Álgebra Lineal , ISBN  978-970-10-6596-9 , Autor: Kozak Ana Maria, Pompeya Pastorelli Sonia, Verdanega Pedro Emilio, Editorial: McGraw-Hill, Edición 2007, 744 páginas, idioma: español
• Allen Hatcher. Topología algebraica. Cambridge University Press, 2002. ISBN 0-521-79540-0 . 
• VV Nikulin, IR Shafarevich. Geometrías y grupos . Springer, 1987. ISBN 3-540-15281-4 , ISBN 978-3-540-15281-1 .  
• "Tore (noción géométrique)" en la Encyclopédie des Formes Mathématiques Remarquables

Busque toro en Wikcionario, el diccionario libre.

Wikimedia Commons tiene medios relacionados con:
Toro (categoría)

• Creación de un toro en el corte del nudo
• "Toro 4D" Secciones transversales de vuelo de un toro de cuatro dimensiones
• "Mapa de perspectiva relacional" Visualización de datos de alta dimensión con un toro plano
• Polydoes, polígonos con forma de rosquilla
• Archivado en Ghostarchive y Wayback Machine: Séquin, Carlo H (27 de enero de 2014). "Topología de un toro torcido – Numberphile" (video) . Brady Haran .
• Anders Sandberg (4 de febrero de 2014). «Torus Earth» . Consultado el 24 de julio de 2019 .