58 (número)
| ||||
|---|---|---|---|---|
| Cardenal | cincuenta y ocho | |||
| Ordinal | 58.º (quincuagésimo octavo) | |||
| Factorización | 2 × 29 | |||
| Divisores | 1, 2, 29, 58 | |||
| Número griego | NO | |||
| Número romano | LVIIII | |||
| Binario | 111010 2 | |||
| Ternario | 2011 3 | |||
| Senador | 134 6 | |||
| Octal | 72 8 | |||
| Duodecimal | 4A 12 | |||
| Hexadecimal | 3A 16 | |||
58 ( cincuenta y ocho ) es el número natural que sigue al 57 y precede al 59 .
Matemáticas
Forma
Cincuenta y ocho es el decimoséptimo semiprimo [1] y el noveno con 2 como el divisor no unitario más bajo ; por tanto de la forma , donde es un primo superior ( 29 ).
Teoría de números
58 es igual a la suma de los primeros siete números primos consecutivos: [2]
Esta es una diferencia de 1 con el decimoséptimo número primo y séptimo superprimo , 59. [3] [4] 58 tiene una suma alícuota de 32 [5] dentro de una secuencia alícuota de dos números compuestos (58, 32, 13 , 1 , 0 ) en el árbol de 13 alícuotas. [6] No hay solución para la ecuación , lo que hace que cincuenta y ocho sea el sexto no cociente ; [7] sin embargo, la función sumatoria tociente sobre los primeros trece números enteros es 58. [8] [a]
Por otra parte, el tociente de Euler de 58 es el segundo número perfecto ( 28 ), [10] donde la suma de los divisores de 58 es el tercer número perfecto unitario ( 90 ).
58 es también el segundo número 11-gonal no trivial , después del 30. [11 ]
Secuencia de biprimos
58 es el segundo miembro del quinto grupo de dos semiprimos o biprimos ( 57 , 58), después de ( 25 , 26 ) y antes de ( 118 , 119 ). [12]
Más específicamente, 58 es el undécimo miembro de la secuencia de semiprimos discretos consecutivos que comienza, [13]
- ( 14 , 15 ), [b]
- (21, 22), [c]
- (33, 34, 35), [d]
- (38, 39)
- (57, 58 )
58 representa el doble de la suma entre los dos primeros biprimos discretos 14 + 15 = 29 , con los dos primeros miembros del primer triplete 33 y 34 (o dos veces 17, el cuarto superprimo ) respectivamente los vigésimo primero y vigésimo segundo números compuestos , [14] y 22 en sí mismo el decimotercer compuesto. [14] (Donde también, 58 es la suma de todos los primos entre 2 y 17.) El primer triplete es el único triplete en la secuencia de biprimos discretos consecutivos cuyos miembros colectivamente tienen factorizaciones primas que casi abarcan un conjunto de números primos consecutivos.
también es semiprimo (el segundo número después de 2 ) . [15]
Propiedades decimales
El quinto dígito es el producto entre el decimotercero y el quincuagésimo octavo número primo,
58 es también el entero más pequeño en decimal cuya raíz cuadrada tiene una fracción continua con período 7. [16] Es el cuarto número de Smith cuya suma de sus dígitos es igual a la suma de los dígitos en su factorización prima (13). [ 17]
Función de Mertens
Dado 58, la función Mertens devuelve , el cuarto número que lo hace. [18] La suma de los primeros tres números que devuelven cero (2, 39 , 40 ) suman 81 = 9 2 , que es el quincuagésimo octavo número compuesto. [14]
Propiedades geométricas
El icosaedro regular produce cincuenta y ocho estelaciones distintas , la mayor cantidad de cualquier otro sólido platónico , que en conjunto producen sesenta y dos estelaciones. [19] [20]
Grupos de Coxeter
Con respecto a los grupos de Coxeter y politopos uniformes en espacios de dimensiones superiores, existen:
- 58 politopos uniformes distintos en la quinta dimensión que se generan a partir de simetrías de tres grupos de Coxeter, son el grupo simplex A 5 , el grupo cúbico B 5 y el grupo demihipercúbico D 5 ;
- 58 grupos fundamentales de Coxeter que generan politopos uniformes en la séptima dimensión , de los cuales sólo cuatro generan figuras uniformes no prismáticas.
Existen 58 grupos de Coxeter paracompactos en total de rangos cuatro a diez, con realizaciones en dimensiones tres a nueve. Todas estas soluciones contienen infinitas facetas y figuras de vértices , a diferencia de los grupos hiperbólicos compactos que contienen elementos finitos; no existen otros grupos de este tipo con rangos superiores o inferiores.
En la ciencia
- El número atómico del cerio (Ce).
Otros campos
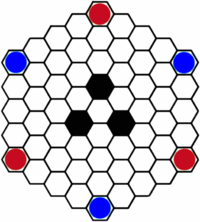
58 es el número de celdas utilizables en un tablero de juego Hexxagon .
Notas
- ^ 58 es también la suma parcial de los primeros ocho registros establecidos por números altamente totientes m con valores φ ( m ) = n : {2, 3, 4, 5, 6, 10, 11, 17 } . [9]
- ^ 14 = 2 · 7 y 15 = 3 · 5, donde los primeros cuatro primos son 2, 3, 5, 7.
- ^ 21 = 3 · 7, y 22 = 2 · 11; factores que abarcan números primos entre 2 y 11 , excepto 5 .
- ^ 33 = 3 · 11, 34 = 2 · 17 y 35 = 5 · 7; en forma similar, un conjunto de factores que son los números primos entre 2 y 17, aparte de 13 ; el último conjunto de factores primos que casi cubre los números primos consecutivos.
Referencias
- ^ Sloane, N. J. A. (ed.). "Secuencia A001358". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
- ^ Sloane, N. J. A. (ed.). "Secuencia A007504 (Suma de los primeros n primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 20 de diciembre de 2022 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A000040 (Los números primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 20 de diciembre de 2022 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A006450 (Primos indexados en primos: primos con subíndices en primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 20 de diciembre de 2022 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A001065 (Suma de divisores propios (o partes alícuotas) de n: suma de divisores de n que son menores que n.)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 27 de febrero de 2024 .
- ^ Sloane, NJA , ed. (1975). "Secuencias alícuotas". Matemáticas de la computación . 29 (129). Fundación OEIS: 101–107 . Consultado el 27 de febrero de 2024 .
- ^ "Sloane's A005278 : Noncototients". La enciclopedia en línea de secuencias de enteros . Fundación OEIS . Consultado el 30 de mayo de 2016 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A002088 (función suma de enteros)". La enciclopedia en línea de secuencias de enteros . Fundación OEIS . Consultado el 27 de febrero de 2024 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A131934 (Registros en A014197.)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 2 de julio de 2024 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A000010 (función totient de Euler)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 2 de julio de 2024 .
- ^ "Sloane's A051682: números 11-gonales". La enciclopedia en línea de secuencias de enteros . Fundación OEIS . Consultado el 30 de mayo de 2016 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A001358 (Semiprimos (o biprimos): productos de dos primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 27 de febrero de 2024 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A006881 (Semiprimos (o biprimos): productos de dos primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 7 de mayo de 2024 .
- ^ abc Sloane, N. J. A. (ed.). "Secuencia A002808 (Los números compuestos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 7 de mayo de 2024 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A104494 (Enteros positivos n tales que n^17 + 1 es semiprimo)". La enciclopedia en línea de secuencias de enteros . Fundación OEIS . Consultado el 27 de febrero de 2024 .
- ^ "Sloane's A013646: Mínimo m tal que la fracción continua para sqrt(m) tiene período n". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 18 de marzo de 2021 .
- ^ "Sloane's A006753: números de Smith". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 30 de mayo de 2016 .
- ^ "Sloane's A028442: Números n tales que la función de Mertens es cero". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 30 de mayo de 2016 .
- ^ HSM Coxeter ; P. Du Val; HT Flather; JF Petrie (1982). Los cincuenta y nueve icosaedros . Nueva York: Springer. doi :10.1007/978-1-4613-8216-4. ISBN . 978-1-4613-8216-4.
- ^ Webb, Robert. "Enumeración de estelaciones". Stella . Archivado desde el original el 2022-11-26 . Consultado el 2023-01-18 .








