100.000
Número natural
← 99999100000100001 →
Cardenalcien mil
Ordinal100000
(cien milésima)
Factorización2 5 × 5 5
Número griego METRO yo {\displaystyle {\stackrel {\iota }{\mathrm {M} }}}
Número romanodo
Binario11000011010100000 2
Ternario12002011201 3
Senador2050544 6
Octal303240 8
Duodecimal49A54 12
Hexadecimal186A0 16
Jeroglífico egipcio𓆐

100.000 ( cien mil ) es el número natural que sigue a 99.999 y precede a 100.001. En notación científica , se escribe 10 5 .

Condiciones para 100.000

En Bangladesh , India , Pakistán y el sur de Asia , cien mil se denomina lakh y se escribe 100 000. Los idiomas tailandés , lao , jemer y vietnamita también tienen palabras separadas para este número: แสน , ແສນ , សែន (all saen ) y ức respectivamente. La palabra malgache es hetsy . [1]

En los Países Bajos , una tonelada es un término coloquial que designa una denominación de 100.000 unidades monetarias. En la época de los florines , una tonelada equivalía a 100.000 florines. Con la introducción del euro, una tonelada pasó a significar 100.000 euros. Su uso se limita principalmente al ámbito financiero y a la compraventa de viviendas. No se utiliza en entornos oficiales debido a la ambigüedad con la tonelada métrica , que se utiliza habitualmente . Si bien su uso es común en los Países Bajos, casi no se utiliza en Bélgica . [ cita requerida ]

En numeración cirílica se le conoce como legión ( легион ):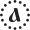o.

Valores de 100.000

En astronomía , 100.000 metros , 100 kilómetros o 100 km (62 millas) es la altitud a la que la Federación Aeronáutica Internacional (FAI) define que comienza el vuelo espacial .

En paleoclimatología , el problema de los 100.000 años es un desajuste entre el registro de temperatura y la radiación solar entrante modelada .

En idioma irlandés , céad míle fáilte ( pronunciado [ˌceːd̪ˠ ˈmʲiːlʲə ˈfˠaːl̠ʲtʲə] ) es un saludo popular que significa "cien mil bienvenidas".

Números seleccionados de 6 dígitos (100 001–999 999)

100.001 a 199.999

  • 147.640 = Número de Keith [15]
  • 148,149 = número de Kaprekar [25]
  • 152,381 = primo único en base 20
  • 156,146 = Número de Keith [15]
  • 155,921 = el número primo más pequeño que es el único primo en un intervalo de 100 n a 100 n + 99
  • 160.000 = 20 4
  • 160,176 = número de árboles reducidos con 26 nodos [26]
  • 161.051 = 11 5
  • 161.280 = número altamente paciente [5]
  • 166.320 = número altamente compuesto [11]
  • 167.400 = número divisor armónico [8]
  • 167.894 = número de formas de particionar {1,2,3,4,5,6,7,8} y luego particionar cada celda (bloque) en subceldas. [27]
  • 173,525 = número de particiones de 49 [7]
  • 173.600 = número divisor armónico [8]
  • 174.680 = Número de Keith [15]
  • 174.763 = Wagstaff primo [28]
  • 176.906 = número de collares de 24 cuentas (se permite darlos vuelta) donde los complementos son equivalentes [29]
  • 177,147 = 3 11
  • 177.777 = el número natural más pequeño que requiere 19 sílabas en inglés americano y 21 en inglés británico
  • 178.478 = Número de Leyland [23]
  • 181.440 = número altamente paciente [5]
  • 181,819 = número de Kaprekar [25]
  • 182.362 = número de collares binarios de 23 cuentas con cuentas de 2 colores en los que los colores se pueden intercambiar pero no se permite darlas vuelta [30]
  • 183,186 = Número de Keith [15]
  • 183.231 = número de conjuntos parcialmente ordenados con 9 elementos sin etiquetar [31]
  • 187,110 = número de Kaprekar [25]
  • 189.819 = número de letras de la palabra más larga en inglés, cuya pronunciación lleva 3 horas [32]
  • 194.481 = 21 4
  • 195.025 = Número de Pell , [33] Número de Markov [24]
  • 196.418 = Número de Fibonacci, [16] Número de Markov [24]
  • 196.560 = el número del beso en 24 dimensiones
  • 196,883 = la dimensión de la representación irreducible no trivial más pequeña del grupo Monstruo
  • 196.884 = el coeficiente de q en la expansión de la serie de Fourier del invariante j . La adyacencia de 196883 y 196884 fue importante para sugerir la existencia de una luz de luna monstruosa .
  • 199.999 = número primo.

200.000 a 299.999

  • 202,717 = k tal que la suma de los cuadrados de los primeros k primos es divisible por k. [34]
  • 206.098 – Número grande de Schröder
  • 206,265 = número redondeado de segundos de arco en un radián (ver también parsec ), ya que180 × 60 × 60/π⁠ = 206.264.806...
  • 207.360 = número altamente paciente [5]
  • 208.012 = el número catalán C 12 [35]
  • 208.335 = el número más grande que puede ser tanto triangular como piramidal cuadrada [36]
  • 208,495 = número de Kaprekar [25]
  • 212.159 = el número más pequeño que no puede ser primo y que termina en 1, 3, 7 o 9 [37] [38]
  • 221.760 = número altamente compuesto [11]
  • 222,222 = dígito de repetición
  • 224.737 = el número primo número 20.000
  • 227,475 = Número de Riordan
  • 234,256 = 22 4
  • 237,510 = número divisor armónico [8]
  • 238,591 = número de 13-ominós libres
  • 241.920 = número altamente paciente [5]
  • 242,060 = número divisor armónico [8]
  • 248.832 = 12 5 , 100.000 12 , también conocido como bruto-gran-bruto (100 12 grandes-brutos); la quinta potencia más pequeña que se puede representar como la suma de solo 6 quintas potencias: 12 5 = 4 5 + 5 5 + 6 5 + 7 5 + 9 5 + 11 5
  • 253,293 = número de nudos primos con 15 cruces
  • 255.168 = número de formas de jugar al tres en raya [39]
  • 262,144 = 2 18 ; factorial exponencial de 4; [40] un número superperfecto [41]
  • 262,468 = Número de Leyland [23]
  • 268.705 = Número de Leyland [23]
  • 271,129 - primo de Sierpiński más pequeño conocido
  • 274,177 = factor primo del número de Fermat F 6
  • 275.807 /195.025 ≈ √2
  • 276,480 = número de polinomios primitivos de grado 24 sobre GF(2) [14]
  • 277.200 = número altamente compuesto [11]
  • 279.841 = 23 4
  • 279,936 = 6 7
  • 280,859 = un número primo cuyo cuadrado 78881777881 es tridigital
  • 291.400 = número de formas no equivalentes de expresar 100.000.000 como la suma de dos números primos [42]
  • 293.547 = Número de Wedderburn–Etherington [20]
  • 294.001 = el número débilmente primo más pequeño en base 10 [43]
  • 294,685 = Número de Markov [24]
  • 298.320 = Número de Keith [15]

300.000 a 399.999

  • 310.572 = Número de Motzkin [12]
  • 314,159 = pi-primo
  • 316.749 = número de árboles reducidos con 27 nodos [26]
  • 317.811 = Número de Fibonacci [16]
  • 317.955 = número de árboles con 19 nodos sin etiquetar [18]
  • 318,682 = número de Kaprekar [25]
  • 325.878 = Número de multa [44]
  • 326,981 = factorial alterno [45]
  • 329,967 = número de Kaprekar [25]
  • 331.776 = 24 4
  • 332.640 = número altamente compuesto; [11] número divisor armónico [8]
  • 333,333 = dígito de repetición
  • 333.667 = fecha de nacimiento sexy y fecha de nacimiento única [46]
  • 333.673 = sexy prime con 333.679
  • 333.679 = sexy prime con 333.673
  • 337.500 = 2 2 × 3 3 × 5 5
  • 337.594 = número de collares de 25 cuentas (se permite darlos vuelta) donde los complementos son equivalentes [29]
  • 349.716 = número de collares binarios de 24 cuentas con cuentas de 2 colores en los que los colores se pueden intercambiar pero no se permite darlas vuelta [30]
  • 351,351 = único número impar abundante conocido que no es la suma de algunos de sus divisores propios, no triviales (es decir, >1) (secuencia A122036 en la OEIS ).
  • 351,352 = número de Kaprekar [25]
  • 355,419 = Número de Keith [15]
  • 356,643 = número de Kaprekar [25]
  • 356.960 = número de polinomios primitivos de grado 23 sobre GF(2) [14]
  • 360,360 = número divisor armónico; [8] número más pequeño divisible por los números del 1 al 15 (no hay número más pequeño divisible por los números del 1 al 14 ya que cualquier número divisible por 3 y 5 debe ser divisible por 15)
  • 362.880 = 9!, número altamente paciente [5]
  • 369,119 = número primo que divide la suma de todos los primos menores o iguales a él [47]
  • 369,293 = el primo más pequeño con la propiedad de que al insertar un dígito en cualquier parte del número siempre se obtendrá un número compuesto [48]
  • 370,261 = primer primo seguido de un espacio entre primos de más de 100
  • 371,293 = 13 5 , palindrómico en base 12 (15AA51 12 )
  • 389,305 = número autodescriptivo en base 7
  • 390,313 = número de Kaprekar [25]
  • 390,625 = 5 8
  • 397,585 = Número de Leyland [23]

400.000 a 499.999

  • 409,113 = suma de los primeros nueve factoriales
  • 422,481 = el número más pequeño cuya cuarta potencia es la suma de tres cuartas potencias más pequeñas
  • 423.393 = Número de Leyland [23]
  • 426.389 = Número de Markov [24]
  • 426,569 = número cíclico en base 12
  • 437.760 a 440.319 =cualquiera de estos números hará que las computadoras Apple II+ y Apple IIe se bloqueen y muestren un mensaje de aviso en el monitor cuando se ingresan en el mensaje de aviso BASIC, debido a un atajo en la programación del código Applesoft de la prueba de desbordamiento al evaluar números de 16 bits. [49] Ingresar 440000 en el mensaje de aviso se ha usado para hackear juegos que están protegidos contra el ingreso de comandos en el mensaje de aviso después de que se carga el juego.
  • 444,444 = dígito de repetición
  • 456.976 = 26 4
  • 461,539 = número de Kaprekar [25]
  • 466,830 = número de Kaprekar [25]
  • 470.832 = Número Pell [33]
  • 483.840 = número altamente paciente [5]
  • 492.638 = número de árboles firmados con 12 nodos [9]
  • 498.960 = número altamente compuesto [11]
  • 499,393 = Número de Markov [24]
  • 499,500 = número de Kaprekar [25]

500.000 a 599.999

  • 500,500 = número de Kaprekar, [25] suma de los primeros 1000 números enteros
  • 509,203 = Riesel de primera calidad [50]
  • 510,510 = el producto de los siete primeros números primos, por lo tanto el séptimo primorial . [51] También es el producto de cuatro números de Fibonacci consecutivos : 13, 21, 34, 55, la mayor secuencia de cualquier longitud que también es un primorial. Y es un número triangular doble , la suma de todos los números pares desde 0 hasta 1428.
  • 514,229 = primo de Fibonacci , [52]
  • 518.859 = Número de Schröder-Hipparchus [4]
  • 524,287 = primo de Mersenne [21]
  • 524.288 = 2 19
  • 524,649 = Número de Leyland [23]
  • 525.600 = minutos en un año no bisiesto
  • 527,040 = minutos en un año bisiesto
  • 531,441 = 3 12
  • 533,169 = Número de Leyland [23]
  • 533,170 = número de Kaprekar [25]
  • 537.824 = 14 5
  • 539,400 = número divisor armónico [8]
  • 548,834 = igual a la suma de las sextas potencias de sus dígitos
  • 554.400 = número altamente compuesto [11]
  • 555,555 = dígito de repetición
  • 586.081 = número de números primos que tienen siete dígitos. [53]
  • 599.999 = número primo.

600.000 a 699.999

  • 604.800 = número de segundos en una semana
  • 614.656 = 28 4
  • 625.992 = Número de Riordan
  • 629.933 = número de árboles reducidos con 28 nodos [26]
  • 645,120 = factorial doble de 14
  • 646,018 = Número de Markov [24]
  • 649.532 = número de collares de 26 cuentas (se permite darlos vuelta) donde los complementos son equivalentes [29]
  • 664.579 = el número de primos menores a 10.000.000
  • 665.280 = número altamente compuesto [11]
  • 665.857 /470.832 ≈ √2
  • 666,666 = dígito de repetición
  • 671.092 = número de collares binarios de 25 cuentas con cuentas de 2 colores en los que los colores se pueden intercambiar pero no se permite darlas vuelta [30]
  • 676.157 = Número de Wedderburn-Etherington [20]
  • 678,570 = Número de campana [13]
  • 694.280 = Número de Keith [15]
  • 695,520 = número divisor armónico [8]

700.000 a 799.999

  • 700.001 = número primo.
  • 707,281 = 29 4
  • 720,720 = número compuesto superior ; [54] número colosalmente abundante ; [55] número más pequeño divisible por los números del 1 al 16
  • 725.760 = número altamente paciente [5]
  • 726,180 = número divisor armónico [8]
  • 729.000 = 90 3
  • 739,397 = primo más grande que se puede truncar tanto por la derecha como por la izquierda .
  • 742.900 = Número catalán [35]
  • 753,480 = número divisor armónico [8]
  • 759,375 = 15 5
  • 762.701 : el número compuesto de Riesel más pequeño conocido
  • 765,623 = emirp , primo de Friedman 5 6 × 7 2 − 6 ÷ 3
  • 777,777 = repdigit, el número natural más pequeño que requiere 20 sílabas en inglés americano, 22 en inglés británico, el número más grande en inglés que no contiene la letra 'i' en su nombre
  • 783.700 = número inicial del siglo III xx 00 a xx 99 (después de 400 y 1.400) que contiene diecisiete números primos [56] [a] {783.701, 783.703, 783.707, 783.719, 783.721, 783.733, 783.737, 783.743, 783.749, 783.763, 783.767, 783.779, 783.781, 783.787, 783.791, 783.793, 783.799}
  • 799,999 = número primo.

800.000 a 899.999

  • 810.000 = 30 4
  • 823.065 = número de árboles con 20 nodos sin etiquetar [18]
  • 823,543 = 7 7
  • 825,265 = el número de Carmichael más pequeño con 5 factores primos
  • 832.040 = Número de Fibonacci [16]
  • 853.467 = Número de Motzkin [12]
  • 857.375 = 95 3
  • 873,612 = 1 1 + 2 2 + 3 3 + 4 4 + 5 5 + 6 6 + 7 7
  • 888,888 = dígito de repetición
  • 890,625 = número automórfico [10]

900.000 a 999.999

  • 900.001 = número primo
  • 901,971 = número de 14-ominós libres
  • 909,091 = primo único en base 10
  • 923,521 = 31 4
  • 925.765 = Número de Markov [24]
  • 925.993 = Número de Keith [15]
  • 950,976 = número divisor armónico [8]
  • 956,619 : 956619^2=915119911161, y solo se utilizan los dígitos 1, 5, 6 y 9 tanto en este número como en su cuadrado .
  • 967.680 = número altamente paciente [5]
  • 970,299 = 99 3 , el cubo de 6 dígitos más grande
  • 998.001 = 999 2 , el cuadrado de 6 dígitos más grande. El recíproco de este número, en su forma expandida, enumera todos los números de tres dígitos en orden excepto 998. [58]
  • 998,991 = el número triangular más grande con 6 dígitos y el número triangular 1413
  • 999,983 = el número primo de 6 dígitos más grande
  • 999,999 = repdigit. Los números racionales con denominadores 7 y 13 tienen repdigit de 6 dígitos cuando se expresan en forma decimal , porque 999999 es el número más pequeño uno menos que una potencia de 10 que es divisible por 7 y por 13, y es el número más grande en inglés que no contiene la letra 'l' en su nombre.

Números primos

Hay 9.592 números primos menores que 10 5 , donde 99.991 es el número primo más grande menor que 100.000.

Los incrementos de 10 5 desde 100.000 hasta un millón tienen los siguientes números primos:

  • 8.392 números primos entre 100.000 y 200.000. [b] Esta es una diferencia de 1.200 números primos con respecto al rango anterior.
    • 104.729 es el número primo número 10.000, que está en este rango.
    • 199.999 es primo.
  • 8.013 números primos entre 200.000 y 300.000. [c] Una diferencia de 379 números primos con respecto al rango anterior.
    • 224.737 es el número primo número 20.000.
  • 7.863 números primos entre 300.000 y 400.000. [d] Una diferencia de 150 números primos con respecto al rango anterior.
    • 350.377 es el número primo número 30.000.
  • 7.678 números primos entre 400.000 y 500.000. [e] Una diferencia de 185 números primos con respecto al rango anterior. Aquí, la diferencia aumenta en un conteo de 35 .
    • 479.909 es el primo número 40.000.
  • 7.560 números primos entre 500.000 y 600.000. [f] Una diferencia de 118 números primos con respecto al rango anterior.
    • 7.560 es el vigésimo número altamente compuesto. [11]
    • 599.999 es primo.
  • 7.445 números primos entre 600.000 y 700.000. [g] Una diferencia de 115 números primos con respecto al rango anterior.
    • 611.953 es el número primo número 50.000.
  • 7.408 números primos entre 700.000 y 800.000. [h] Una diferencia de 37 números primos con respecto al rango anterior.
    • 700.001 y 799.999 son ambos números primos.
    • 746.773 es el número primo número 60.000.
  • 7.323 números primos entre 800.000 y 900.000. [i] Una diferencia de 85 números primos con respecto al rango anterior. Aquí, la diferencia aumenta en un conteo de 48 .
    • 882.377 es el número primo número 70.000.
  • 7224 números primos entre 900 000 y 1 000 000. [j] Una diferencia de 99 números primos con respecto al rango anterior . La diferencia aumenta nuevamente, en un conteo de 14 .
    • 900.001 es primo.

En total, hay 68.906 números primos entre 100.000 y 1.000.000. [59]

Notas

  1. ^ No hay siglos que contengan más de diecisiete números primos entre 200 y 122.853.771.370.899 inclusive. [57]
  2. ^ El p más pequeño > 100 000 es 100 003 (9593.º); el p más grande < 200 000 es 199 999 (17 984.º).
  3. ^ El p más pequeño > 200 000 es 200 003 (17 985.º); el p más grande < 300 000 es 299 993 (25 997.º).
  4. ^ El p más pequeño > 300 000 es 300 007 (número 25 998); el p más grande < 400 000 es 399 989 (número 33 860).
  5. ^ El p más pequeño > 400 000 es 400 009 (33 861.º); el p más grande < 500 000 es 499 979 (41 538.º).
  6. ^ El p más pequeño > 500 000 es 500 009 (41 539.º); el p más grande < 600 000 es 599 999 (49 098.º).
  7. ^ El p más pequeño > 600 000 es 600 011 (49 099.º); el p más grande < 700 000 es 699 967 (56 543.º).
  8. ^ El p más pequeño > 700 000 es 700 001 (56 544.º); el p más grande < 800 000 es 799 999 (63 951.º).
  9. ^ El p más pequeño > 800 000 es 800 011 (puesto 63 952); el p más grande < 900 000 es 899 981 (puesto 71 274).
  10. ^ El p más pequeño > 900 000 es 900 001 (71 275.º); el p más grande < 1 000 000 es 999 983 (78 498.º).

Referencias

  1. ^ "Diccionario malgache y enciclopedia de Madagascar: hetsy". malagasyword.org . 26 de octubre de 2017 . Consultado el 31 de diciembre de 2019 .
  2. ^ Sloane, N. J. A. (ed.). "Secuencia A003617 (primo de n dígitos más pequeño)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  3. ^ "Problema del mes (agosto de 2000)". Archivado desde el original el 18 de diciembre de 2012. Consultado el 13 de enero de 2013 .
  4. ^ ab Sloane, N. J. A. (ed.). "Secuencia A001003 (Segundo problema de Schroeder (paréntesis generalizados); también llamados números supercatalanos o pequeños números de Schroeder.)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  5. ^ abcdefghij Sloane, Nueva Jersey (ed.). "Secuencia A097942 (Números muy pacientes)". La enciclopedia en línea de secuencias enteras . Fundación OEIS.
  6. ^ Sloane, N. J. A. (ed.). "Secuencia A006785 (Número de grafos sin triángulos en n vértices)". La enciclopedia en línea de secuencias de enteros . Fundación OEIS.
  7. ^ abcd Sloane, N. J. A. (ed.). "Secuencia A000041 (a(n) es el número de particiones de n (los números de partición))". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  8. ^ abcdefghijklm Sloane, N. J. A. (ed.). "Secuencia A001599 (Números armónicos o de Ore)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  9. ^ ab Sloane, N. J. A. (ed.). "Secuencia A000060 (Número de árboles con signo con n nodos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  10. ^ ab Sloane, N. J. A. (ed.). "Secuencia A003226 (Números automórficos: m^2 termina en m)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  11. ^ abcdefghi Sloane, N. J. A. (ed.). "Secuencia A002182 (Números altamente compuestos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  12. ^ abc Sloane, N. J. A. (ed.). "Secuencia A001006 (números de Motzkin)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  13. ^ ab Sloane, N. J. A. (ed.). "Secuencia A000110 (números Bell o exponenciales)". La enciclopedia en línea de secuencias enteras . Fundación OEIS.
  14. ^ abc Sloane, N. J. A. (ed.). "Secuencia A011260 (Número de polinomios primitivos de grado n sobre GF(2))". La enciclopedia en línea de secuencias de enteros . Fundación OEIS.
  15. ^ abcdefghij Sloane, N. J. A. (ed.). "Secuencia A007629 (números Repfigit (REPetitive FIbonacci-like diGIT) (o números de Keith))". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  16. ^ abcd Sloane, N. J. A. (ed.). "Secuencia A000045 (números de Fibonacci)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  17. ^ Sloane, N. J. A. (ed.). "Secuencia A049363 (a(1) = 1; para n > 1, el número más pequeño balanceado digitalmente en base n)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  18. ^ abc Sloane, N. J. A. (ed.). "Secuencia A000055 (Número de árboles con n nodos sin etiquetar)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  19. ^ Sloane, N. J. A. (ed.). "Secuencia A002104 (Números logarítmicos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  20. ^ abc Sloane, N. J. A. (ed.). "Secuencia A001190 (números Wedderburn-Etherington)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  21. ^ ab Sloane, N. J. A. (ed.). "Secuencia A000668 (primos de Mersenne (primos de la forma 2^n - 1))". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  22. ^ Sloane, N. J. A. (ed.). "Secuencia A003432 (problema del determinante máximo de Hadamard)". La enciclopedia en línea de secuencias de enteros . Fundación OEIS . Consultado el 30 de marzo de 2024 .
  23. ^ abcdefgh Sloane, N. J. A. (ed.). "Secuencia A076980 (números de Leyland)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  24. ^ abcdefgh Sloane, N. J. A. (ed.). "Secuencia A002559 (números de Markoff (o Markov))". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  25. ^ abcdefghijklmn Sloane, N. J. A. (ed.). "Secuencia A006886 (números de Kaprekar)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  26. ^ abc Sloane, N. J. A. (ed.). "Secuencia A000014 (Número de árboles de series reducidas con n nodos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  27. ^ Sloane, N. J. A. (ed.). "Secuencia A000258 (Expansión de egf exp(exp(exp(x)-1)-1))". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  28. ^ Sloane, N. J. A. (ed.). "Secuencia A000979 (primos de Wagstaff)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  29. ^ abc Sloane, N. J. A. (ed.). "Secuencia A000011 (Número de collares de n cuentas (se permite darlos vuelta) donde los complementos son equivalentes)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  30. ^ abc Sloane, N. J. A. (ed.). "Secuencia A000013 (Definición (1): Número de collares binarios de n cuentas con cuentas de 2 colores donde los colores se pueden intercambiar pero no se permite darlas vuelta)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  31. ^ Sloane, N. J. A. (ed.). "Secuencia A000112 (Número de conjuntos parcialmente ordenados (posets) con n elementos no etiquetados)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  32. ^ "¿La palabra más larga en inglés? Aquí están las 15 más largas". Berlitz . Consultado el 1 de marzo de 2024 .
  33. ^ ab Sloane, N. J. A. (ed.). "Secuencia A000129 (números de Pell)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  34. ^ Sloane, N. J. A. (ed.). "Secuencia A111441 (Números k tales que la suma de los cuadrados de los primeros k primos es divisible por k)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  35. ^ ab Sloane, N. J. A. (ed.). "Secuencia A000108 (números catalanes)". La enciclopedia en línea de secuencias enteras . Fundación OEIS.
  36. ^ Sloane, N. J. A. (ed.). "Secuencia A000330 (Números piramidales cuadrados: a(n) = 0^2 + 1^2 + 2^2 + ... + n^2 = n*(n+1)*(2*n+1)/6)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  37. ^ Collins, Julia (2019). Números en minutos . Reino Unido: Quercus. p. 140. ISBN 978-1635061772.
  38. ^ Sloane, N. J. A. (ed.). "Secuencia A143641 (Números primos impares que no terminan en 5)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  39. ^ "¿Cuántos juegos de tres en raya (tres en raya)?".
  40. ^ Sloane, N. J. A. (ed.). "Secuencia A049384 (a(0)=1, a(n+1) = (n+1)^a(n))". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  41. ^ Sloane, N. J. A. (ed.). "Secuencia A019279 (Números superperfectos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  42. ^ Sloane, N. J. A. (ed.). "Secuencia A065577 (Número de particiones Goldbach de 10^n)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  43. ^ Weißstein, Eric W. (25 de diciembre de 2020). "Prima débil". Wolfram MathWorld .
  44. ^ Sloane, N. J. A. (ed.). "Secuencia A000957 (secuencia de Fine (o números de Fine): número de relaciones de valencia mayores o iguales a 1 en un conjunto n; también número de árboles ordenados con raíz y n aristas que tienen raíz de grado par)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  45. ^ Sloane, N. J. A. (ed.). "Secuencia A005165 (Factoriales alternados)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  46. ^ Sloane, N. J. A. (ed.). "Secuencia A040017 (Primos de período único)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  47. ^ Sloane, N. J. A. (ed.). "Secuencia A007506 (Primos p con propiedad de que p divide la suma de todos los primos <= p)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  48. ^ Sloane, N. J. A. (ed.). "Secuencia A125001 (Primos no insertables: primos con la propiedad de que, sin importar dónde insertes (o antepongas o añadas) un dígito, obtienes un número compuesto (excepto si antepones un cero).)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  49. ^ "Desmontaje de Applesoft -- S.d912". Archivado desde el original el 15 de abril de 2016. Consultado el 4 de abril de 2016 .ROM desmontada. Ver comentarios en $DA1E.
  50. ^ Sloane, N. J. A. (ed.). "Secuencia A101036 (números de Riesel)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  51. ^ Sloane, N. J. A. (ed.). "Secuencia A002110 (Números primordiales)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  52. ^ Sloane, N. J. A. (ed.). "Secuencia A005478 (números primos de Fibonacci)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.Sloane, N. J. A. (ed.). "Secuencia A178444 (números de Markov que son primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  53. ^ Sloane, N. J. A. (ed.). "Secuencia A006879 (Número de primos con n dígitos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  54. ^ Sloane, N. J. A. (ed.). "Secuencia A002201 (Números altamente compuestos superiores)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  55. ^ Sloane, N. J. A. (ed.). "Secuencia A004490 (Números colosalmente abundantes)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  56. ^ Sloane, N. J. A. (ed.). "Secuencia A186509 (centurias que contienen 17 primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  57. ^ Sloane, N. J. A. (ed.). "Secuencia A186311 (menos de 100k a 100k+99 con exactamente n primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  58. ^ "Dividir uno por 998001 produce una lista de números de tres dígitos". 23 de enero de 2012.
  59. ^ Caldwell, Chris K. "La página Nth Prime". PrimePages . Consultado el 3 de diciembre de 2022 .De las diferencias de los índices primos de los números primos más pequeños y más grandes en rangos de incrementos de 10 5 , más 1 (para cada rango).
Obtenido de "https://es.wikipedia.org/w/index.php?title=100.000&oldid=1258158391"