Órdenes de magnitud (números)
Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes )
|

Esta lista contiene números positivos seleccionados en orden creciente, incluidos los recuentos de cosas, cantidades adimensionales y probabilidades . A cada número se le asigna un nombre en la escala corta , que se utiliza en los países de habla inglesa, así como un nombre en la escala larga , que se utiliza en algunos de los países que no tienen el inglés como idioma nacional.
Menor que 10-100(un googolth)

- Matemáticas – selecciones aleatorias: Aproximadamente 10 −183,800 es una primera estimación aproximada de la probabilidad de que un " mono " que escribe, o un robot que escribe sin saber inglés, cuando se coloca frente a una máquina de escribir , escriba la obra Hamlet de William Shakespeare como su primer conjunto de entradas, con la condición previa de que escriba la cantidad necesaria de caracteres. [1] Sin embargo, al exigir una puntuación , mayúsculas y espaciado correctos , la probabilidad cae a alrededor de 10 −360,783 . [2]
- Cálculo: 2,2 × 10 −78913 es aproximadamente igual al valor distinto de cero más pequeño que puede representarse mediante un valor de punto flotante IEEE de precisión óctuple .
- 1 × 10 −6176 es igual al valor distinto de cero más pequeño que puede representarse mediante un valor de punto flotante decimal IEEE de precisión cuádruple .
- 6,5 × 10 −4966 es aproximadamente igual al valor distinto de cero más pequeño que puede representarse mediante un valor de punto flotante IEEE de precisión cuádruple .
- 3,6 × 10 −4951 es aproximadamente igual al valor distinto de cero más pequeño que puede representarse mediante un valor de punto flotante IEEE de doble extensión x86 de 80 bits .
- 1 × 10 −398 es igual al valor distinto de cero más pequeño que puede representarse mediante un valor de punto flotante decimal IEEE de doble precisión .
- 4,9 × 10 −324 es aproximadamente igual al valor distinto de cero más pequeño que puede representarse mediante un valor de punto flotante IEEE de doble precisión .
- 1,5 × 10−157 es aproximadamente igual a la probabilidad de que en un grupo de 365 personas seleccionadas al azar, todas tengan cumpleaños diferentes . [3]
- 1 × 10 −101 es igual al valor distinto de cero más pequeño que puede representarse mediante un valor de punto flotante decimal IEEE de precisión simple .
10-100hasta 10-30

- Matemáticas: Las probabilidades de barajar una baraja estándar de 52 cartas en cualquier orden específico son de alrededor de 1,24 × 10 −68 (o exactamente 1 ⁄ 52! ) [4]
- Computación: El número 1,4 × 10 −45 es aproximadamente igual al valor positivo distinto de cero más pequeño que puede representarse mediante un valor de punto flotante IEEE de precisión simple .
10-30
( 0,000 000 000 000 000 000 000 000 000 001 ; 1000 −10 ; escala corta : una nonillonésima; escala larga : una quintillonésima )
ISO: quecto- (q)
- Matemáticas: La probabilidad en una partida de bridge de que los cuatro jugadores obtengan un palo completo cada uno es aproximadamente4,47 × 10 −28 . [5]
10−27
( 0.000 000 000 000 000 000 000 000 001 ; 1000 −9 ; escala corta : una octillonésima; escala larga : una cuadrillonésima )
ISO: ronto- (r)
10-24
( 0,000 000 000 000 000 000 000 001 ; 1000 −8 ; escala corta : una septillonésima; escala larga : una cuatrillónésima)
ISO: yocto- (y)
10-21
( 0,000 000 000 000 000 000 001 ; 1000 −7 ; escala corta : una sextillonésima; escala larga : una trillionésima)
ISO: zepto- (z)
- Matemáticas: La probabilidad de acertar 20 números para 20 en un juego de keno es de aproximadamente 2,83 × 10 −19 .
- Matemáticas: Las probabilidades de un grupo perfecto en el torneo de baloncesto masculino de la División I de la NCAA son de 1 en 2 63 , aproximadamente 1,08 × 10 −19 , si se utilizan lanzamientos de moneda para predecir los ganadores de los 63 partidos. [6]
10-18

( 0,000 000 000 000 000 001 ; 1000 −6 ; escala corta : una quintillonésima; escala larga : una billonésima)
ISO: atto- (a)
- Matemáticas: La probabilidad de que salgan ojos de serpiente 10 veces seguidas en un par de dados justos es de aproximadamente2,74 × 10 −16 .
10-15
( 0,000 000 000 000 001 ; 1000 −5 ; escala corta : una cuatrillónésima; escala larga : una billonésima)
ISO: femto- (f)
- Matemáticas : La constante de Ramanujan es un número casi entero , que difiere del número entero más cercano en aproximadamente7,5 × 10 −13 .
10-12
( 0,000 000 000 001 ; 1000 −4 ; escala corta : una billonésima; escala larga : una milmillonésima)
ISO: pico- (p)
- Matemáticas: La probabilidad en una partida de bridge de que un jugador obtenga un palo completo es aproximadamente2,52 × 10 −11 ( 0,000 000 002 52 % ).
- Biología: La sensibilidad visual humana a la luz de 1000 nm es de aproximadamente1,0 × 10 −10 de su sensibilidad máxima a 555 nm . [7]
10-9
( 0,000 000 001 ; 1000 −3 ; escala corta : una milmillonésima; escala larga : una milmillonésima)
ISO: nano- (n)
- Matemáticas – Lotería: Las probabilidades de ganar el Gran Premio (acertar los 6 números) en la lotería Powerball de EE. UU. , con un solo boleto, según las reglas a partir de octubre de 2015 [update], son de 292.201.338 a 1 en contra, para una probabilidad de3,422 × 10 −9 ( 0,000 000 342 2 % ).
- Matemáticas – Lotería: Las probabilidades de ganar el Gran Premio (acertar los 6 números) en la lotería Powerball australiana , con un solo boleto, según las reglas a abril de 2018 [update], son 134.490.400 a 1 en contra, para una probabilidad de7,435 × 10 −9 ( 0,000 000 743 5 % ).
- Matemáticas – Lotería: Las probabilidades de ganar el Jackpot (acertar los 6 números principales) en la Lotería Nacional del Reino Unido , con un solo boleto, según las reglas a partir de agosto de 2009 [update], son de 13.983.815 a 1 en contra, para una probabilidad de7,151 × 10 −8 ( 0,000 007 151 % ).
10-6
( 0,000 001 ; 1000 −2 ; escalas larga y corta : una millonésima)
ISO: micro- (μ)

| Mano | Oportunidad |
|---|---|
| 1. Escalera real | 0,000 15% |
| 2. Escalera de color | 0,0014% |
| 3. Cuatro de un tipo | 0,024% |
| 4. Casa llena | 0,14% |
| 5. Enjuague | 0,19% |
| 6. Recto | 0,59% |
| 7. Tres iguales | 2,1% |
| 8. Dos pares | 4,8% |
| 9. Un par | 42% |
| 10. Sin par | 50% |
- Matemáticas – Póquer : Las probabilidades de obtener una escalera real en el póquer son de 649.739 a 1, lo que da una probabilidad de 1,5 × 10−6 ( 0,000 15% ). [8]
- Matemáticas – Póquer: Las probabilidades de obtener una escalera de color (que no sea una escalera real) en el póquer son de 72.192 a 1, lo que da una probabilidad de 1,4 × 10-5 (0,0014%).
- Matemáticas – Póquer: Las probabilidades de que te repartan cuatro cartas iguales en el póquer son de 4.164 a 1, lo que supone una probabilidad de 2,4 × 10-4 (0,024%).
10-3
(0,001; 1000 −1 ; una milésima )
ISO: mili- (m)
- Matemáticas – Póker: Las probabilidades de que te repartan un full en el póker son de 693 a 1, lo que supone una probabilidad de 1,4 × 10 −3 (0,14%).
- Matemáticas – Póker: Las probabilidades de obtener un color en el póker son de 507,8 a 1, lo que supone una probabilidad de 1,9 × 10 −3 (0,19%).
- Matemáticas – Póker: Las probabilidades de que te repartan una escalera en el póker son de 253,8 a 1, lo que supone una probabilidad de 4 × 10 −3 (0,39%).
- Física: α =0,007 297 352 570 (5) , la constante de estructura fina .
10-2
(0,01; una centésima )
ISO: centi- (c)
- Matemáticas – Lotería: Las probabilidades de ganar cualquier premio en la Lotería Nacional del Reino Unido , con un solo boleto, bajo las reglas de 2003, son de 54 a 1, para una probabilidad de aproximadamente 0,018 (1,8%).
- Matemáticas – Póker: Las probabilidades de que salga un trío en el póker son de 46 a 1, lo que supone una probabilidad de 0,021 (2,1%).
- Matemáticas – Lotería: Las probabilidades de ganar cualquier premio en el Powerball , con un solo boleto, bajo las reglas a partir de 2015, son de 24,87 a 1 en contra, para una probabilidad de 0,0402 (4,02%).
- Matemáticas – Póker: Las probabilidades de recibir dos pares en el póker son de 21 a 1, lo que supone una probabilidad de 0,048 (4,8%).
10-1
(0,1; una décima parte)
ISO: deci- (d)
- Historia legal : El 10% era un impuesto muy extendido recaudado sobre los ingresos o productos en el período antiguo y medieval; véase diezmo .
- Matemáticas – Póker: Las probabilidades de recibir solo un par en el póker son de aproximadamente 5 a 2 (2,37 a 1), para una probabilidad de 0,42 (42%).
- Matemáticas – Póker: Las probabilidades de no recibir ningún par en el póker son de casi 1 a 2, lo que supone una probabilidad de aproximadamente 0,5 (50%).
100

(1; uno )
- Demografía: La población de Monowi , una aldea incorporada en Nebraska , Estados Unidos , era de uno en 2010.
- Religión: Uno es el número de dioses en el judaísmo , el cristianismo y el islam ( religiones monoteístas ).
- Informática – Unicode : Se asigna un carácter al bloque Unicode del Suplemento Lisu , la menor cantidad de todos los bloques Unicode de uso público a partir de Unicode 15.0 (2022).
- Matemáticas: √ 2 ≈ 1.414 213 562 373 095 049 , la relación entre la diagonal de un cuadrado y la longitud de su lado.
- Matemáticas: φ ≈ 1.618 033 988 749 894 848 , la proporción áurea .
- Matemáticas: √ 3 ≈ 1.732 050 807 568 877 293 , la relación de la diagonal de un cubo unitario .
- Matemáticas: el sistema numérico que entienden la mayoría de las computadoras, el sistema binario , utiliza 2 dígitos: 0 y 1.
- Matemáticas: √ 5 ≈ 2.236 067 9775, correspondiente a la diagonal de un rectángulo cuyos lados miden 1 y 2.
- Matemáticas: √ 2 + 1 ≈ 2.414 213 562 373 095 049 , la razón de plata ; la razón de la menor de las dos cantidades a la cantidad mayor es la misma que la razón de la cantidad mayor a la suma de la cantidad menor y el doble de la cantidad mayor.
- Matemáticas: e ≈ 2,718 281 828 459 045 087 , la base del logaritmo natural .
- Matemáticas: el sistema numérico que entienden las computadoras ternarias , el sistema ternario , utiliza 3 dígitos: 0, 1 y 2.
- Religión: tres manifestaciones de Dios en la Trinidad cristiana .
- Matemáticas: π ≈ 3,141 592 653 589 793 238 , la relación entre la circunferencia de un círculo y su diámetro.
- Religión: las Cuatro Nobles Verdades del Budismo.
- Biología: 7 ± 2 , en ciencia cognitiva , estimación de George A. Miller del número de objetos que pueden mantenerse simultáneamente en la memoria de trabajo humana .
- Música : 7 notas en escala mayor o menor .
- Astronomía: 8 planetas del Sistema Solar .
- Religión: el Noble Óctuple Sendero en el Budismo.
- Literatura: Los 9 círculos del Infierno en el Infierno de Dante Alighieri .
101

(10; diez )
ISO: deca- (da)
- Demografía: La población de Pesnopoy , un pueblo de Bulgaria , era de 10 en 2007.
- Escala humana: Hay 10 dedos en un par de manos humanas , y 10 dedos en un par de pies humanos .
- Matemáticas: El sistema numérico utilizado en la vida cotidiana, el sistema decimal , tiene 10 dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- Religión: los Diez Mandamientos en las religiones abrahámicas .
- Música: El número de notas (12) en una escala cromática .
- Astrología: Hay 12 signos del zodíaco , cada uno de los cuales representa parte de la trayectoria anual del movimiento del sol a través del cielo nocturno.
- Informática – Microsoft Windows : Hasta diciembre de 2021 se han lanzado doce versiones sucesivas de Windows NT para el consumidor.
- Música: El número (15) de cuartetos de cuerdas completos y numerados de Ludwig van Beethoven y Dmitri Shostakovich .
- Lingüística: El idioma finlandés tiene quince casos nominales .
- Matemáticas: El sistema hexadecimal , un sistema numérico común utilizado en programación informática, utiliza 16 dígitos donde los últimos 6 suelen estar representados por letras: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
- Computación – Unicode: El tamaño mínimo posible de un bloque Unicode es de 16 puntos de código contiguos (es decir, U+ abcde 0 - U+ abcde F).
- Computación – UTF-16 / Unicode : Hay 17 planos direccionables en UTF-16 y, por lo tanto, como Unicode está limitado al espacio de código UTF-16, hay 17 planos válidos en Unicode.
- Ciencia ficción: El enigma 23 juega un papel destacado en la trama de la trilogía Illuminatus! de Robert Shea y Robert Anton Wilson .
- Matemáticas: e π ≈ 23,140692633
- Música: un total combinado de 24 tonalidades mayores y menores , además del número de obras de algunos ciclos musicales de JS Bach , Frédéric Chopin , Alexander Scriabin y Dmitri Shostakovich .
- Escritura alfabética: hay 26 letras en el alfabeto inglés derivado del latín (excluyendo las letras que se encuentran solo en préstamos extranjeros).
- Ciencia ficción: El número 42, en la novela Guía del autoestopista galáctico de Douglas Adams , es la respuesta a la pregunta fundamental de la vida, el universo y todo lo que se calcula mediante una enorme supercomputadora durante un período de 7,5 millones de años.
- Biología: Cada célula humana contiene 46 cromosomas .
- Fonología: Hay 47 fonemas en la fonología inglesa en la pronunciación recibida .
- Escritura silábica: hay 49 letras en cada uno de los dos silabarios kana ( hiragana y katakana ) utilizados para representar al japonés (sin contar las letras que representan patrones de sonido que nunca han ocurrido en japonés).
- Ajedrez : Cualquiera de los jugadores en una partida de ajedrez puede reclamar tablas si cada bando realiza 50 movimientos consecutivos sin ninguna captura o movimiento de peón.
- Demografía: La población de la isla Nassau , parte de las Islas Cook , era de alrededor de 78 habitantes en 2016.
- Escritura silábica: Hay 85 letras en la versión moderna del silabario Cherokee .
- Música: Hay 88 teclas en un piano de cola .
- Computación – ASCII : Hay 95 caracteres imprimibles en el conjunto de caracteres ASCII .
102
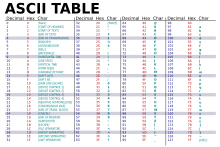
(100; cien )
ISO: hecto- (h)
- Historia europea: Las agrupaciones de 100 granjas eran una unidad administrativa común en el norte de Europa y Gran Bretaña (véase Cien (división de condado) ).
- Música: Hay 104 sinfonías numeradas de Franz Josef Haydn .
- Religión: 108 es un número sagrado en el hinduismo .
- Química: hasta 2016 se han descubierto o sintetizado 118 elementos químicos .
- Computación – ASCII: Hay 128 caracteres en el conjunto de caracteres ASCII , incluidos los caracteres de control no imprimibles .
- Videojuegos: Hay 151 Pokémon en la primera generación .
- Fonología: Se estima que la lengua Taa tiene entre 130 y 164 fonemas distintos.
- Ciencia política: En 2011, las Naciones Unidas contaban con 193 Estados miembros .
- Computación: Una imagen GIF (o una imagen de 8 bits ) admite un máximo de 256 (=2 8 ) colores.
- Computación – Unicode: Hay 327 bloques Unicode diferentes a partir de Unicode 15.0 (2022).
- Aviación: 583 personas murieron en el desastre del aeropuerto de Tenerife de 1977 , el accidente más mortífero no causado por una acción terrorista deliberada en la historia de la aviación civil.
- Música: El número más grande (626) en el catálogo Köchel de obras de Wolfgang Amadeus Mozart .
- Demografía: La Ciudad del Vaticano , el país independiente menos poblado, tiene una población aproximada de 800 habitantes en 2018.
103

( 1 000 ; mil )
ISO: kilo- (k)
- Demografía: La población de la Isla Ascensión es de 1.122 habitantes.
- Música: 1.128: número de obras conocidas existentes de Johann Sebastian Bach reconocidas en el Bach-Werke-Verzeichnis hasta 2017.
- Composición tipográfica: 2000 a 3000 letras en una página de texto mecanografiada típica .
- Matemáticas: 2,520 (5×7×8×9 o 2 3 ×3 2 ×5×7) es el mínimo común múltiplo de todo entero positivo menor que (e incluido) 10.
- Terrorismo: 2.996 personas (incluidos 19 terroristas) murieron en los ataques terroristas del 11 de septiembre de 2001 .
- Biología: el ADN de los virus más simples tiene 3.000 pares de bases . [9]
- Historia militar : 4.200 (República) o 5.200 (Imperio) era el tamaño estándar de una legión romana .
- Lingüística: Las estimaciones sobre la diversidad lingüística de las lenguas o dialectos humanos vivos varían entre 5.000 y 10.000. ( En 2009, SIL Ethnologue enumeró 6.909 lenguas vivas conocidas).
- Astronomía – Catálogos: Hay 7.840 objetos de cielo profundo en el Catálogo NGC desde 1888.
- Lexicografía: 8.674 palabras únicas en la Biblia hebrea .
104
( 10 000 ; diez mil o una miríada )
- Biología: Se estima que cada neurona del cerebro humano se conecta a otras 10.000.
- Demografía: La población de Tuvalu era de 10.544 habitantes en 2007.
- Lexicografía: 14.500 palabras únicas en inglés aparecen en la versión King James de la Biblia.
- Zoología: Se conocen aproximadamente 17.500 especies distintas de mariposas. [10]
- Idioma: Existen entre 20.000 y 40.000 caracteres chinos distintos que se usan de forma ocasional.
- Biología: Se estima que cada ser humano tiene 20.000 genes codificantes . [11]
- Gramática: Cada verbo regular en cherokee puede tener 21.262 formas flexivas .
- Guerra: 22.717 soldados de la Unión y la Confederación murieron, resultaron heridos o desaparecieron en la Batalla de Antietam , el día de batalla más sangriento en la historia de Estados Unidos.
- Informática – Unicode: 42.720 caracteres están codificados en CJK Unified Ideographs Extension B , la mayor cantidad de cualquier bloque Unicode de uso público a partir de Unicode 15.0 (2022).
- Aviación: Hasta julio de 2021 [update], se han construido más de 44.000 fuselajes del Cessna 172 , el avión más producido de la historia .
- Informática - Fuentes: El número máximo posible de glifos en una fuente TrueType u OpenType es 65.535 (2 16 -1), el número más grande representable por el entero sin signo de 16 bits utilizado para registrar el número total de glifos en la fuente.
- Computación – Unicode: Un plano contiene 65.536 (2 16 ) puntos de código; este es también el tamaño máximo de un bloque Unicode y el número total de puntos de código disponibles en la codificación obsoleta UCS-2 .
- Matemáticas: 65.537 es el mayor primo de Fermat conocido .
- Memoria: A partir de 2015 [update], el mayor número de decimales de π que se han recitado de memoria es 70.030. [12]
105

( 100 000 ; cien mil o un lakh ).
- Demografía: La población de San Vicente y las Granadinas era de 100.982 habitantes en 2009.
- Biología – Hebras de cabello en la cabeza: La cabeza humana promedio tiene alrededor de 100.000 a 150.000 hebras de cabello .
- Literatura: aproximadamente 100.000 versos ( shlokas ) en el Mahabharata .
- Informática – Unicode: 149.186 caracteres (incluidos los caracteres de control) codificados en Unicode a partir de la versión 15.0 (2022).
- Idioma: 267.000 palabras en el Ulises de James Joyce .
- Computación – Unicode: 293.168 puntos de código asignados a un bloque Unicode a partir de Unicode 15.0.
- Genocidio: 300.000 personas asesinadas en la masacre de Nanjing .
- Idioma – Palabras en inglés: El New Oxford Dictionary of English contiene alrededor de 360.000 definiciones de palabras en inglés .
- Matemáticas: 360.000: el número aproximado de entradas en la Enciclopedia en línea de secuencias de números enteros a enero de 2023. [update][ 13]
- Biología – Plantas: Se conocen aproximadamente 390.000 especies de plantas distintas, de las cuales aproximadamente el 20% (o 78.000) están en riesgo de extinción. [14]
- Biología – Flores: Hay aproximadamente 400.000 especies distintas de flores en la Tierra. [15]
- Literatura: 564.000 palabras en Guerra y paz de León Tolstoi .
- Literatura: 930.000 palabras en la versión King James de la Biblia.
- Matemáticas: Hay 933.120 combinaciones posibles en el Pyraminx .
- Computación – Unicode: Hay 974.530 puntos de código asignables públicamente (es decir, no sustitutos, puntos de código de uso privado o no caracteres) en Unicode.
106

( 1 000 000 ; 1000 2 ; escalas larga y corta : un millón )
ISO: mega- (M)
- Demografía: La población de Riga , Letonia era de 1.003.949 en 2004, según Eurostat .
- Computación – UTF-8 : Hay 1.112.064 (2 20 + 2 16 - 2 11 ) secuencias UTF-8 válidas (excluidas las secuencias demasiado largas y las secuencias correspondientes a puntos de código utilizados para sustitutos UTF-16 o puntos de código más allá de U+10FFFF).
- Computación – UTF-16 /Unicode: Hay 1.114.112 (2 20 + 2 16 ) valores distintos codificables en UTF-16 y, por lo tanto (dado que Unicode está actualmente limitado al espacio de código UTF-16), 1.114.112 puntos de código válidos en Unicode (1.112.064 valores escalares y 2.048 sustitutos).
- Ludología – Número de juegos: Se han creado aproximadamente 1.181.019 videojuegos hasta 2019. [16]
- Biología – Especies: El Instituto de Recursos Mundiales afirma que se han identificado aproximadamente 1,4 millones de especies , de un número desconocido de especies totales (las estimaciones varían entre 2 y 100 millones de especies). Algunos científicos dan 8,8 millones de especies como cifra exacta.
- Genocidio: Aproximadamente entre 800.000 y 1.500.000 (1,5 millones) de armenios fueron asesinados en el genocidio armenio .
- Lingüística: El número de conjugaciones posibles para cada verbo en la lengua Archi es 1.502.839. [17]
- Información: La base de datos freedb de listados de pistas de CD tiene alrededor de 1.750.000 entradas a junio de 2005 [update].
- Informática – UTF-8: 2.164.864 (2 21 + 2 16 + 2 11 + 2 7 ) posibles secuencias UTF-8 de uno a cuatro bytes, si no se respetan las restricciones sobre secuencias demasiado largas, puntos de código sustitutos y puntos de código superiores a U+10FFFF . (Tenga en cuenta que no todos estos corresponden a puntos de código únicos).
- Matemáticas – Naipes: Hay 2.598.960 manos de póquer diferentes de 5 cartas que se pueden repartir con una baraja estándar de 52 cartas.
- Matemáticas: Hay 3.149.280 posiciones posibles para el Skewb .
- Matemáticas – Cubo de Rubik: 3.674.160 es el número de combinaciones del Cubo de bolsillo (Cubo de Rubik 2×2×2).
- Geografía/Informática – Lugares geográficos: El servidor de nombres NIMA GEOnet contiene aproximadamente 3,88 millones de características geográficas con nombre fuera de los Estados Unidos, con 5,34 millones de nombres. El sistema de información de nombres geográficos del USGS afirma tener casi 2 millones de características geográficas físicas y culturales dentro de los Estados Unidos.
- Computación - Hardware de supercomputadora: 4.981.760 núcleos de procesador en la configuración final de la supercomputadora Tianhe-2 .
- Genocidio: Aproximadamente entre 5.100.000 y 6.200.000 judíos fueron asesinados en el Holocausto .
- Información – Sitios web: Al 18 de octubre de 2024, la Wikipedia en inglés contiene aproximadamente 6,9 millones de artículos en el idioma inglés .
107

( 10 000 000 ; un crore ; escalas larga y corta : diez millones )
- Demografía: La población de Haití era de 10.085.214 en 2010.
- Literatura: 11.206.310 palabras en Devta de Mohiuddin Nawab , la historia más larga publicada de forma continua conocida en la historia de la literatura.
- Genocidio : Se estima que 12 millones de personas fueron enviadas desde África al Nuevo Mundo en el tráfico de esclavos del Atlántico .
- Matemáticas: 12.988.816 es el número de fichas de dominó de un tablero de ajedrez de 8×8 .
- Genocidio/Hambruna: 15 millones es el límite inferior estimado para el número de muertos de la Gran Hambruna China de 1959-1961 , la hambruna más letal conocida en la historia de la humanidad.
- Guerra: Se estima que hubo entre 15 y 22 millones de víctimas como consecuencia de la Primera Guerra Mundial .
- Computación: Se pueden generar 16.777.216 colores diferentes utilizando el sistema de código hexadecimal en HTML (tenga en cuenta que la visión de color tricromática del ojo humano solo puede distinguir entre aproximadamente 1.000.000 de colores diferentes). [18]
- Ciencia ficción : En el Imperio Galáctico de Isaac Asimov , en el año 22.500 d.C., hay 25.000.000 de planetas habitados diferentes en el Imperio Galáctico, todos habitados por humanos en el escenario de la "galaxia humana" de Asimov.
- Genocidio/Hambruna: 55 millones es el límite máximo estimado para el número de muertos por la Gran Hambruna China.
- Literatura: Wikipedia contiene un total de alrededor de 63 millones de artículos en 352 idiomas en octubre de 2024.
- Guerra: Se estima que hubo entre 70 y 85 millones de víctimas como consecuencia de la Segunda Guerra Mundial .
- Matemáticas: 73.939.133 es el mayor primo truncable por la derecha .
108
( 100 000 000 ; escalas larga y corta : cien millones )
- Demografía: La población de Filipinas era de 100.981.437 en 2015.
- Internet – YouTube: Se estima que el número de canales de YouTube es de 113,9 millones. [19]
- Información – Libros: La Biblioteca Británica tiene más de 150 millones de artículos. La Biblioteca del Congreso tiene aproximadamente 148 millones de artículos. Ver La galaxia Gutenberg .
- Videojuegos: En 2020 se han vendido [update]aproximadamente 200 millones de copias de Minecraft (el videojuego más vendido de la historia).
- Matemáticas: Más de 215.000.000 de constantes matemáticas se han recopilado en el inversor de Plouffe[update] a partir de 2010. [20]
- Matemáticas: 275.305.224 es el número de cuadrados mágicos normales de 5×5 , sin contar rotaciones ni reflexiones. Este resultado fue hallado en 1973 por Richard Schroeppel .
- Demografía: La población de los Estados Unidos era 328,239,523 en 2019.
- Matemáticas: 358.833.097 estelaciones del triacontaedro rómbico .
- Información – Sitios web: A partir de noviembre de 2011 [update], la encuesta web de Netcraft estima que existen 525.998.433 (526 millones) de sitios web distintos .
- Astronomía – Estrellas catalogadas: El Catálogo de Estrellas Guía II tiene entradas sobre 998.402.801 objetos astronómicos distintos .
109
( 1 000 000 000 ; 1000 3 ; escala corta : mil millones ; escala larga : mil millones, o un billón )
ISO: giga- (G)
- Transporte – Automóviles: A partir de 2018 [update], hay aproximadamente 1.400 millones de automóviles en el mundo, lo que corresponde a alrededor del 18% de la población humana. [21]
- Demografía – China: 1.409.670.000 – población aproximada de la República Popular China en 2023. [22]
- Demografía – India 1.428.627.663 – población aproximada de la India en 2023. [23]
- Demografía – África: La población de África alcanzó los 1.430.000.000 en algún momento de 2023.
- Internet – Google: Hay más de 1.500.000.000 de usuarios activos de Gmail en todo el mundo. [24]
- Internet: En octubre de 2015 había aproximadamente 1.500.000.000 de usuarios activos en Facebook. [25]
- Computación – Límite computacional de una CPU de 32 bits : 2.147.483.647 es igual a 2 · 31 −1 y, como tal, es el número más grande que puede caber en un entero con signo ( complemento a dos ) de 32 bits en una computadora.
- Computación – UTF-8: 2.147.483.648 (2 31 ) puntos de código posibles (U+0000 - U+7FFFFFFF) en la versión anterior a 2003 de UTF-8 (incluidas secuencias de cinco y seis bytes), antes de que el espacio de código UTF-8 se limitara al conjunto mucho más pequeño de valores codificables en UTF-16 .
- Biología – pares de bases en el genoma: aproximadamente 3,3 × 109 pares de bases en el genoma humano. [11]
- Lingüística : 3.400.000.000 – el número total de hablantes de lenguas indoeuropeas , de los cuales 2.400.000.000 son hablantes nativos; los otros 1.000.000.000 hablan lenguas indoeuropeas como segunda lengua.
- Matemáticas y computación : 4.294.967.295 (2 32 − 1), el producto de los cinco primos de Fermat conocidos y el valor máximo para un entero sin signo de 32 bits en computación.
- Computación – IPv4 : 4.294.967.296 (2 32 ) posibles direcciones IP únicas .
- Computación: 4.294.967.296 – la cantidad de bytes en 4 gibibytes ; en computación, las computadoras de 32 bits pueden acceder directamente a 2 32 unidades (bytes) de espacio de direcciones, lo que conduce directamente al límite de 4 gigabytes en la memoria principal.
- Matemáticas: 4.294.967.297 es un número de Fermat y semiprimo . Es el número más pequeño de la forma que no es un número primo .
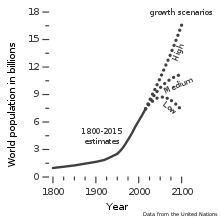
- Demografía – población mundial : 8.019.876.189 – Población estimada para el mundo al 1 de enero de 2024. [26]
1010
( 10 000 000 000 ; escala corta : diez mil millones ; escala larga : diez mil millones, o diez mil millones )
- Biología – bacterias en el cuerpo humano: Hay aproximadamente 10 10 bacterias en la boca humana . [27]
- Informática – páginas web: aproximadamente 5,6 × 1010 páginas web indexadas por Google en 2010.
1011
( 100 000 000 000 ; escala corta : cien mil millones ; escala larga : cien mil millones o cien mil millones )
- Astronomía: Hay 100 mil millones de planetas ubicados en la Vía Láctea. [28] [29]
- Biología – Neuronas en el cerebro: aproximadamente (1±0,2) × 10 11 neuronas en el cerebro humano . [30]
- Medicina: La Administración de Alimentos y Medicamentos de los Estados Unidos requiere un mínimo de 3 x 10 11 (300 mil millones) de plaquetas por unidad de aféresis . [31]
- Paleodemografía – Número de humanos que alguna vez vivieron : aproximadamente (1,2 ± 0,3) × 10 11 nacidos vivos de humanos anatómicamente modernos desde el comienzo del Paleolítico Superior . [32]
- Astronomía – estrellas en nuestra galaxia: del orden de 10 11 estrellas en la galaxia de la Vía Láctea . [33]
- Matemáticas: 608.981.813.029 es el número más pequeño para el cual hay más primos de la forma 3 k + 1 que de la forma 3 k + 2 hasta el número. [34]
1012
.jpg/440px-Andromeda_Galaxy_(with_h-alpha).jpg)
( 1 000 000 000 000 ; 1000 4 ; escala corta : un billón; escala larga : mil millones)
ISO: tera- (T)
- Astronomía: La galaxia de Andrómeda , que forma parte del mismo Grupo Local que nuestra galaxia , contiene alrededor de 10 12 estrellas.
- Biología – Bacterias en el cuerpo humano: La superficie del cuerpo humano alberga aproximadamente 10 12 bacterias . [27]
- Astronomía – Galaxias : Una estimación de 2016 dice que hay 2 × 10 12 galaxias en el universo observable . [35]
- Biología – Células sanguíneas en el cuerpo humano: El cuerpo humano promedio tiene 2,5 × 10 12 glóbulos rojos. [ cita médica necesaria ]
- Biología: Se estima que en 2015 había 3,04 × 10 12 árboles en la Tierra. [36]
- Biología marina : 3.500.000.000.000 (3,5 × 10 12 ) – población estimada de peces en el océano. [ cita requerida ]
- Matemáticas : 7.625.597.484.987 – un número que aparece a menudo cuando se trata de potencias de 3. Se puede expresar como , , y 3 3 o cuando se utiliza la notación de flecha hacia arriba de Knuth, se puede expresar como y .
- Astronomía: Un año luz , según la definición de la Unión Astronómica Internacional (UAI), es la distancia que recorre la luz en el vacío en un año, lo que equivale a unos 9,46 billones de kilómetros (9,46 × 10 12 kilómetros ).
- Matemáticas: 10 13 – El número aproximado de ceros no triviales conocidos de la función zeta de Riemann a partir de 2004. [update][ 37]
- Matemáticas – Dígitos conocidos de π : A marzo de 2019 [update], el número de dígitos conocidos de π es 31.415.926.535.897 (la parte entera de π × 1013 ). [38]
- Biología : aproximadamente 10 14 sinapsis en el cerebro humano. [39]
- Biología – Células en el cuerpo humano: El cuerpo humano consta de aproximadamente 10 14 células , de las cuales solo 10 13 son humanas. [40] [41] El 90% restante de células no humanas (aunque mucho más pequeñas y constituyen una masa mucho menor) son bacterias , que residen principalmente en el tracto gastrointestinal, aunque la piel también está cubierta de bacterias.
- Matemáticas: El primer caso de exactamente 18 números primos entre múltiplos de 100 es 122.853.771.370.900 + n , [42] para n = 1, 3, 7, 19, 21, 27, 31, 33, 37, 49, 51, 61, 69, 73, 87, 91, 97, 99.
- Criptografía: 150.738.274.937.250 configuraciones de la placa de conexión de la máquina Enigma utilizada por los alemanes en la Segunda Guerra Mundial para codificar y decodificar mensajes mediante cifrado.
- Computación – MAC-48 : 281.474.976.710.656 (2 48 ) posibles direcciones físicas únicas .
- Matemáticas: 953.467.954.114.363 es el primo de Motzkin más grande conocido .
1015

( 1 000 000 000 000 000 ; 1000 5 ; escala corta : un cuatrillón ; escala larga : mil billones, o un billón)
ISO: peta- (P)
- Biología – Insectos : 1.000.000.000.000.000 a 10.000.000.000.000.000 (10 15 a 10 16 ): el número total estimado de hormigas vivas en la Tierra en un momento dado (su biomasa es aproximadamente igual a la biomasa total de la especie humana ). [43]
- Cálculo: 9.007.199.254.740.992 (2 53 ) – número hasta el cual todos los valores enteros pueden representarse exactamente en formato de punto flotante de doble precisión IEEE .
- Matemáticas: 48.988.659.276.962.496 es el quinto número de taxi .
- Ciencia ficción : En el Imperio Galáctico de Isaac Asimov , en lo que llamamos 22.500 d.C., hay 25.000.000 de planetas habitados diferentes en el Imperio Galáctico, todos habitados por humanos en el escenario de la "galaxia humana" de Asimov, cada uno con una población promedio de 2.000.000.000, lo que arroja una población total del Imperio Galáctico de aproximadamente 50.000.000.000.000.000.
- Ciencia ficción : Hay aproximadamente 10 17 seres sensibles en la galaxia de Star Wars .
- Criptografía: Hay 2 56 = 72.057.594.037.927.936 claves posibles diferentes en el cifrado simétrico DES de 56 bits obsoleto .
1018

( 1 000 000 000 000 000 000 ; 1000 6 ; escala corta : un quintillón ; escala larga : un billón)
ISO: exa- (E)
- Matemáticas: El primer caso de exactamente 19 números primos entre múltiplos de 100 es 1.468.867.005.116.420.800 + n , [42] para n = 1, 3, 7, 9, 21, 31, 37, 39, 43, 49, 51, 63, 67, 69, 73, 79, 81, 87, 93.
- Matemáticas: La conjetura de Goldbach ha sido verificada para todos los n ≤ 4 × 1018 mediante un proyecto que calculó todos los números primos hasta ese límite. [44]
- Computación – Manufactura: Se estima que 6 × 10 En 2008 se produjeron 18 transistores en todo el mundo. [45]
- Computación – Límite computacional de una CPU de 64 bits : 9,223,372,036,854,775,807 (aproximadamente 9,22 × 1018 ) es igual a 2 63 −1 y, como tal, es el número más grande que puede caber en un entero con signo ( complemento a dos ) de 64 bits en una computadora.
- Matemáticas – Torneo de baloncesto de la NCAA : Hay 9.223.372.036.854.775.808 (2 63 ) formas posibles de ingresar al grupo .
- Matemáticas – Bases : 9,439,829,801,208,141,318 (≈9.44 × 1018 ) es el décimo y (por conjetura) mayor número con más de un dígito que puede escribirse desde la base 2 hasta la base 18 usando solo los dígitos del 0 al 9, lo que significa que los dígitos del 10 al 17 no son necesarios en bases mayores que 10. [46]
- Biología – Insectos: Se ha estimado que la población de insectos de la Tierra es de aproximadamente 10 19 . [47]
- Matemáticas – Respuesta al problema del trigo y el tablero de ajedrez : Al duplicar los granos de trigo en cada cuadrado sucesivo de un tablero de ajedrez , comenzando con un grano de trigo en el primer cuadrado, el número final de granos de trigo en los 64 cuadrados del tablero de ajedrez cuando se suman es 2 64 −1 = 18.446.744.073.709.551.615 (≈1,84 × 1019 ).
- Matemáticas – Leyendas: La leyenda de la Torre de Brahma habla de un templo hindú que contiene una gran sala con tres postes, en uno de los cuales hay 64 discos dorados , y el objetivo del juego matemático es que los brahmanes en este templo muevan todos los discos a otro poste para que estén en el mismo orden, nunca colocando un disco más grande sobre un disco más pequeño, moviendo solo uno a la vez. Usando el algoritmo más simple para mover los discos, se necesitarían 2 64 −1 = 18,446,744,073,709,551,615 (≈1.84 × 1019 ) vueltas para completar la tarea (el mismo número que en el problema del trigo y el tablero de ajedrez anterior). [48]
- Computación – IPv6 : 18.446.744.073.709.551.616 (2 64 ; ≈1,84 × 1019 ) posibles subredes únicas /64 .
- Matemáticas – Cubo de Rubik: Hay 43.252.003.274.489.856.000 (≈4,33 × 1019 ) diferentes posiciones de un cubo de Rubik de 3×3×3.
- Fuerza de la contraseña : el uso del conjunto de 95 caracteres que se encuentra en los teclados de computadora estándar para una contraseña de 10 caracteres produce un valor computacionalmente intratable de 59,873,693,923,837,890,625 (95 10 , aproximadamente 5.99 × 1019 ) permutaciones.
- Economía: La hiperinflación en Zimbabwe fue estimada en febrero de 2009 por algunos economistas en 10 sextillones por ciento, [49] o un factor de 10 20 .
1021

( 1 000 000 000 000 000 000 000 ; 1000 7 ; escala corta : un sextillón ; escala larga : mil billones, o un trillón )
ISO: zetta- (Z)
- Geo – Granos de arena: Se ha estimado que todas las playas del mundo juntas contienen aproximadamente entre 10 y 21 granos de arena . [50]
- Computación – Fabricación: Intel predijo que habría 1,2 × 1021 transistores en el mundo en 2015 [51] y Forbes estimó que 2,9 × 10Hasta 2014 se habían enviado 21 transistores . [52]
- Matemáticas – Sudoku: Hay 6.670.903.752.021.072.936.960 (≈6,7 × 1021 ) Cuadrículas de sudoku de 9×9 . [53]
- Matemáticas: El primer caso de exactamente 20 números primos entre múltiplos de 100 es 20.386.095.164.137.273.086.400 + n , [42] para n = 1, 3, 7, 9, 13, 19, 21, 31, 33, 37, 49, 57, 63, 73, 79, 87, 91, 93, 97, 99.
- Astronomía – Estrellas: 70 sextillones = 7 × 1022 , el número estimado de estrellas dentro del alcance de los telescopios (en 2003). [54]
- Astronomía – Estrellas: en el rango de 10 23 a 10 24 estrellas en el universo observable . [55]
- Matemáticas: 146.361.946.186.458.562.560.000 (≈1,5 × 1023 ) es el quinto número perfecto unitario .
- Matemáticas: 357.686.312.646.216.567.629.137 (≈3,6 × 1023 ) es el primo truncable por la izquierda más grande .

- Química – Física: La constante de Avogadro (6.022 140 76 × 10 23 ) es el número de constituyentes (por ejemplo, átomos o moléculas) en un mol de una sustancia, definido por conveniencia como la expresión del orden de magnitud que separa la escala molecular de la macroscópica .
1024
( 1 000 000 000 000 000 000 000 000 ; 1000 8 ; escala corta : un septillón ; escala larga : un cuatrillón)
ISO: yotta- (Y)
- Matemáticas: 2.833.419.889.721.787.128.217.599 (≈2,8 × 1024 ) es el quinto primo de Woodall .
- Matemáticas: 3.608.528.850.368.400.786.036.725 (≈3,6 × 1024 ) es el número polidivisible más grande .
- Matemáticas: 2 86 = 77.371.252.455.336.267.181.195.264 es la mayor potencia de dos conocida que no contiene el dígito '0' en su representación decimal. [56]
1027
( 1 000 000 000 000 000 000 000 000 000 ; 1000 9 ; escala corta : un octillón ; escala larga : mil cuatrillones o un cuatrillón)
ISO: ronna- (R)
- Biología – Átomos en el cuerpo humano: el cuerpo humano promedio contiene aproximadamente 7 × 1027 átomos . [57]
- Matemáticas – Póquer: la cantidad de combinaciones únicas de manos y cartas compartidas en un juego de Texas Hold'em de 10 jugadores es aproximadamente 2,117 × 1028 .
1030
.jpg/440px-E._coli_Bacteria_(7316101966).jpg)
( 1 000 000 000 000 000 000 000 000 000 000 ; 1000 10 ; escala corta : un nonillón ; escala larga : un quintillón )
ISO: quetta- (Q)
- Biología – Células bacterianas en la Tierra: Se estima que el número de células bacterianas en la Tierra es de 5.000.000.000.000.000.000.000.000.000.000, o 5 × 10 30 . [58]
- Matemáticas: 5.000.000.000.000.000.000.000.000.000.027 es el primo cuasi-mínimo más grande.
- Matemáticas: El número de particiones de 1000 es 24.061.467.864.032.622.473.692.149.727.991. [59]
- Matemáticas: 3 68 = 278.128.389.443.693.511.257.285.776.231.761 es la mayor potencia de tres conocida que no contiene el dígito "0" en su representación decimal.
- Matemáticas: 2 108 = 324.518.553.658.426.726.783.156.020.576.256 es la mayor potencia de dos conocida que no contiene el dígito '9' en su representación decimal. [60]
- Matemáticas: 7 39 = 909.543.680.129.861.140.820.205.019.889.143 es la mayor potencia conocida de 7 que no contiene el dígito '7' en su representación decimal.
1033
( 1 000 000 000 000 000 000 000 000 000 000 000 ; 1000 11 ; escala corta : un decillón ; escala larga : mil quintillones o un quintillón)
- Matemáticas – Estrella de Alejandro: Hay 72.431.714.252.715.638.411.621.302.272.000.000 (aproximadamente 7,24 × 1034 ) diferentes posiciones de la Estrella de Alejandro .
1036
( 1 000 000 000 000 000 000 000 000 000 000 000 000 ; 1000 12 ; escala corta : un undecillón ; escala larga : un sextillón )
- Matemáticas: 2 2 7 −1 − 1 = 170,141,183,460,469,231,731,687,303,715,884,105,727 (≈1.7 × 1038 ) es el primo doble de Mersenne más grande conocido .
- Cálculo: 2 128 = 340.282.366.920.938.463.463.374.607.431.768.211.456 (≈3,40282367 × 1038 ), el número máximo teórico de direcciones de Internet que se pueden asignar bajo el sistema de direccionamiento IPv6 , uno más que el valor más grande que se puede representar mediante un valor de punto flotante IEEE de precisión simple, el número total de diferentes identificadores universalmente únicos (UUID) que se pueden generar.
- Criptografía: 2 128 = 340.282.366.920.938.463.463.374.607.431.768.211.456 (≈3,40282367 × 1038 ), el número total de claves posibles diferentes en el espacio de clave AES de 128 bits(cifrado simétrico).
1039
( 1 000 000 000 000 000 000 000 000 000 000 000 000 000 ; 1000 13 ; escala corta : un duodecillón ; escala larga : mil sextillones, o un sextilliardo)
- Cosmología: El número de Eddington-Dirac es aproximadamente 10 40 .
- Matemáticas: 97# × 2 5 × 3 3 × 5 × 7 = 69,720,375,229,712,477,164,533,808,935,312,303,556,800 (≈6.97 × 1040 ) es el mínimo común múltiplo de todo número entero del 1 al 100.
1042hasta 10100
( 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 ; 1000 14 ; escala corta : un tredecillón ; escala larga : un septillón )
- Matemáticas: 141×2 141 +1 = 393.050.634.124.102.232.869.567.034.555.427.371.542.904.833 (≈3,93 × 1044 ) es el segundo primo de Cullen .
- Matemáticas: Hay 7.401.196.841.564.901.869.874.093.974.498.574.336.000.000.000 (≈7,4 × 1045 ) posibles permutaciones para el Cubo de Rubik (Cubo de Rubik 4×4×4).

- Ajedrez : 4,52 × 1046 es un límite superior probado para el número de posiciones de ajedrez permitidas según las reglas del ajedrez . [61]
- Geometría : 1,33 × 1050 es el número estimado de átomos en la Tierra .
- Matemáticas: 2 168 = 374.144.419.156.711.147.060.143.317.175.368.453.031.918.731.001.856 es la mayor potencia de dos conocida que no es pandigital : no hay ningún dígito '2' en su representación decimal. [62]
- Matemáticas: 3 106 = 375.710.212.613.636.260.325.580.163.599.137.907.799.836.383.538.729 es la mayor potencia de tres conocida que no es pandigital: no existe el dígito '4'. [62]
- Matemáticas: 808.017.424.794.512.875.886.459.904.961.710.757.005.754.368.000.000.000 (≈8,08 × 1053 ) es el orden del grupo de monstruos .
- Criptografía: 2 192 = 6,277,101,735,386,680,763,835,789,423,207,666,416,102,355,444,464,034,512,896 (6.27710174 × 1057 ), el número total de claves posibles diferentes en el espacio de claves de 192 bits del Estándar de cifrado avanzado (AES) (cifrado simétrico).
- Cosmología: 8 × 1060 es aproximadamente el número deintervalos de tiempo de Planck desde que se teoriza que el universo se creó en el Big Bang hace 13.799 ± 0.021 mil millones de años. [63]
- Cosmología: 1 × 1063 es la estimación que hizo Arquímedes en su Calculador de arena del número total de granos de arena que podrían caber en todo el cosmos , cuyo diámetro estimó en estadios en lo que llamamos 2 años luz .
- Matemáticas – Cartas: 52 ! = 80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440,883,277,824,000,000,000,000 (≈8.07 × 1067 ) – el número de formas de ordenar las cartas en una baraja de 52 cartas.
- Matemáticas: Hay ≈1,01×10 68 combinaciones posibles para el Megaminx .
- Matemáticas: 1.808.422.353.177.349.564.546.512.035.512.530.001.279.481.259.854.248.860.454.348.989.451.026.887 (≈1,81 × 1072 ) – El factor primo más grande conocidoencontrado mediante factorización de curva elíptica de Lenstra (LECF) hasta 2010.[update][ 64]
- Matemáticas: Hay 282.870.942.277.741.856.536.180.333.107.150.328.293.127.731.985.672.134.721.536.000.000.000.000.000 (≈2,83 × 1074 ) posibles permutaciones del Cubo del Profesor (Cubo de Rubik 5×5×5).
- Criptografía: 2 256 = 115.792.089.237.316.195.423.570.985.008.687.907.853.269.984.665.640.564.039.457.584.007.913.129.639.936 (≈1,15792089 × 1077 ), el número total de claves posibles diferentes en el espacio de clave de 256 bits del Estándar de cifrado avanzado (AES) (cifrado simétrico).
- Cosmología: Varias fuentes estiman que el número total de partículas fundamentales en el universo observable está dentro del rango de 10 80 a 10 85 . [65] [66] Sin embargo, estas estimaciones generalmente se consideran como conjeturas. (Compárese con el número de Eddington , el número total estimado de protones en el universo observable).
- Computación: 9,999 999 × 1096 es igual al valor más grande que se puede representar en el formato de punto flotante decimal32 IEEE .
- Computación: 69! (aproximadamente 1,7112245 × 1098 ), es el valor factorial más grande que se puede representar en una calculadora con dos dígitos para potencias de diez sin desbordamiento.
- Matemáticas: Un googol , 1 × 10100 , 1 seguido de cien ceros, o 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000.
10100(un googol) a 101000
( 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 ; escala corta : diez duotrigentillones; escala larga : diez mil sexdecillones , o diez sexdecillones) [ 67]
- Matemáticas: Hay 157 152 858 401 024 063 281 013 959 519 483 771 508 510 790 313 968 742 344 694 684 829 502 629 887 168 573 442 107 637 760 000 000 000 000 000 000 000 000 (≈1,57 × 10116 ) permutaciones distinguibles del V-Cube 6 (Cubo de Rubik 6×6×6).
- Ajedrez: Número de Shannon , 10 120 , un límite inferior de la complejidad del árbol de juego del ajedrez.
- Física: 10 120 , discrepancia entre el valor observado de la constante cosmológica y una estimación ingenua basada en la teoría cuántica de campos y la energía de Planck .
- Física: 8 × 10120 , relación entre la masa y la energía en el universo observable y la energía de un fotón con una longitud de onda del tamaño del universo observable .
- Matemáticas: 19 568 584 333 460 072 587 245 340 037 736 278 982 017 213 829 337 604 336 734 362 294 738 647 777 395 483 196 097 971 852 999 259 921 329 236 506 842 360 439 300 (≈1,96 × 10121 ) es el período de los pseudoprimos de Fermat .
- Historia – Religión: Asaṃkhyeya es un nombre budista para el número 10 140. Aparece en el Avatamsaka Sutra y metafóricamente significa "innumerable" en el idioma sánscrito de la antigua India .
- Xiangqi: 10 150 , una estimación de la complejidad del árbol de juego de xiangqi .
- Matemáticas: Hay 19 500 551 183 731 307 835 329 126 754 019 748 794 904 992 692 043 434 567 152 132 912 323 232 706 135 469 180 065 278 712 755 853 360 682 328 551 719 137 311 299 993 600 000 000 000 000 000 000 000 000 000 000 000 (≈1,95 × 10160 ) permutaciones distinguibles del V-Cube 7 (Cubo de Rubik 7×7×7).

- Ir: Hay 208 168 199 381 979 984 699 478 633 344 862 770 286 522 453 884 530 548 425 639 456 820 927 419 612 738 015 378 525 648 451 698 519 643 907 259 916 015 628 128 546 089 888 314 427 129 715 319 317 557 736 620 397 247 064 840 935 (≈2,08 × 10170 ) posiciones legales en el juego de Go. Véase Go y matemáticas .
- Economía: La tasa anualizada de hiperinflación en Hungría en 1946 se estimó en 2,9 × 10177 %. [68] Fue el caso más extremo de hiperinflación jamás registrado.
- Juegos de mesa: 3,457 × 10181 , número de formas de organizar las fichas del Scrabble inglés en un tablero de Scrabble estándar de 15 por 15.
- Física: 10 186 , número aproximado de volúmenes de Planck en el universo observable .
- Shogi: 10 226 , una estimación de la complejidad del árbol de juego del shogi .
- Física: 7×10 245 , volumen espacio-temporal aproximado de la historia del universo observable en unidades de Planck . [69]
- Computación: 1.797 693 134 862 315 807 × 10308 es aproximadamente igual al valor más grande que se puede representar en el formato de punto flotante de doble precisión IEEE .
- Cálculo: (10 – 10 −15 ) × 10384 es igual al valor más grande que se puede representar en el formato de punto flotante decimal64 IEEE .
- Matemáticas: 997# × 31# × 7 × 5 2 × 3 4 × 2 7 = 7 128 865 274 665 093 053 166 384 155 714 272 920 668 358 861 885 893 040 452 001 991 154 324 087 581 111 499 476 444 151 913 871 586 911 717 817 019 575 256 512 980 264 067 621 009 251 465 871 004 305 131 072 686 268 143 200 196 609 974 862 745 937 188 343 705 015 434 452 523 739 745 298 963 145 674 982 128 236 956 2 823 794 011 068 809 262 317 708 861 979 540 791 247 754 558 049 326 475 737 829 923 352 751 796 735 248 042 463 638 051 137 034 331 214 781 746 850 878 453 485 678 021 888 075 373 249 921 995 672 056 932 029 099 390 891 687 487 672 697 950 1 603 520 000 (≈7,13 × 10432 ) es el mínimo común múltiplo de todo número entero del 1 al 1000.
101000hasta 1010 100(un googolplex)
- Matemáticas: Hay aproximadamente 1,869 × 104099 permutaciones distinguibles del cubo de Rubik más grande del mundo (33×33×33).
- Computación: 1.189 731 495 357 231 765 05 × 104932 es aproximadamente igual al valor más grande que se puede representar en elformato de punto flotante de precisión extendida IEEE 80 bits x86.
- Computación: 1.189 731 495 357 231 765 085 759 326 628 007 0 × 104932 es aproximadamente igual al valor más grande que se puede representar en el formato de punto flotante de cuádruple precisión IEEE .
- Cálculo: (10 – 10 −33 ) × 106144 es igual al valor más grande que se puede representar en el formato de punto flotante decimal128 IEEE .
- Computación: 10 10,000 − 1 es igual al mayor valor que se puede representar en la calculadora de Windows Phone .
- Matemáticas: 104.824 5 + 5 104.824 es el mayor primo de Leyland probado ; con 73.269 dígitos a abril de 2023. [update][ 70]
- Matemáticas: aproximadamente 7,76 × 10 206.544 cabezas de ganado en el rebaño más pequeño que satisface las condiciones del problema del ganado de Arquímedes .
- Matemáticas: 2.618.163.402.417 × 2 1.290.000 − 1 es un primo de Sophie Germain de 388.342 dígitos ; el más grande conocido a abril de 2023. [update][ 71]
- Matemáticas: 2.996.863.034.895 × 2 1.290.000 ± 1 son primos gemelos de 388.342 dígitos ; el mayor conocido hasta abril de 2023. [update][ 72]
- Matemáticas: 3.267.113# – 1 es un primo primo de 1.418.398 dígitos ; el más grande conocido a fecha de abril de 2023. [update][ 73]
- Matemáticas – Literatura: La Biblioteca de Babel de Jorge Luis Borges contiene al menos 25 1.312.000 ≈ 1,956 × 10 1.834.097 libros (este es un límite inferior). [74]
- Matemáticas: 10 1.888.529 − 10 944.264 – 1 es un primo palindrómico de 1.888.529 dígitos , el mayor conocido hasta abril de 2023. [update][ 75]
- Matemáticas: 4 × 72 1.119.849 − 1 es el primo más pequeño de la forma 4 × 72 n − 1. [76]
- Matemáticas: 422.429! + 1 es un primo factorial de 2.193.027 dígitos ; el mayor conocido hasta abril de 2023. [update][ 77]
- Matemáticas: (2 15.135.397 + 1)/3 es un primo probable de Wagstaff de 4.556.209 dígitos , el más grande conocido a junio de 2021 [update].
- Matemáticas: 1.963.736 1.048.576 + 1 es un primo de Fermat generalizado de 6.598.776 dígitos , el mayor conocido a fecha de abril de 2023. [update][ 78]
- Matemáticas: (10 8.177.207 − 1)/9 es un primo probable de 8.177.207 dígitos , el mayor conocido a fecha del 8 de mayo de 2021. [update][ 79]
- Matemáticas: 10,223 × 2 31,172,165 + 1 es un primo de Proth de 9,383,761 dígitos , el primo de Proth más grande conocido [80] y primo no Mersenne hasta 2021. [update][ 81]
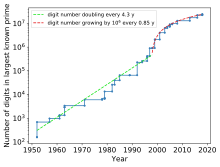
- Matemáticas: 2 82.589.933 − 1 es un primo de Mersenne de 24.862.048 dígitos ; el primo más grande conocido de cualquier tipo hasta 2020. [update][ 81]
- Matemáticas: 2 82.589.932 × (2 82.589.933 − 1) es un número perfecto de 49.724.095 dígitos , el mayor conocido hasta el año 2020. [82]
- Matemáticas – Historia: 10 8×10 16 , el mayor número nombrado en el Calculador de Arena de Arquímedes .
- Matemáticas: 10 googol ( ), un googolplex . Un número 1 seguido de 1 googol de ceros. Carl Sagan ha estimado que 1 googolplex, completamente escrito, no cabría en el universo observable debido a su tamaño, aunque también señaló que uno también podría escribir el número como 10 10 100 . [83]
Mayor de 1010 100
(Un googolplex ; 10 googol ; escala corta : googolplex; escala larga : googolplex)
- Go: Existen al menos 10 10 108 juegos de Go legales. Ver Complejidad del árbol de juegos .
- Matemáticas – Literatura: El número de formas diferentes en que se pueden ordenar los libros de la Biblioteca de Babel de Jorge Luis Borges es aproximadamente , el factorial del número de libros de la Biblioteca de Babel.
- Cosmología: En la teoría de la inflación caótica , propuesta por el físico Andrei Linde , nuestro universo es uno de muchos otros universos con diferentes constantes físicas que se originaron como parte de nuestra sección local del multiverso , debido a un vacío que no se había desintegrado a su estado fundamental . Según Linde y Vanchurin, el número total de estos universos es de aproximadamente . [84]
- Matemáticas: , orden de magnitud de un límite superior que ocurrió en una prueba de Skewes (más tarde se estimó que estaba más cerca de 1.397 × 10 316 ).
- Cosmología: Se estima que el número estimado de unidades de tiempo de Planck para las fluctuaciones cuánticas y el efecto túnel para generar un nuevo Big Bang es .
- Matemáticas: , un número de la familia googol llamado googolplexplex, googolplexiano o googolduplex. 1 seguido de un googolplex ceros, o 10 googolplex
- Cosmología: La estimación más alta del tamaño del universo entero es aproximadamente 2 veces el del universo observable . [85]
- Matemáticas: , orden de magnitud de otro límite superior en una prueba de Skewes .
- Matemáticas: El mega de Steinhaus se encuentra entre 10[4]257 y 10[4]258 (donde a [ n ] b es la hiperoperación ).
- Matemáticas: El número de Moser, "2 en un megagono" en notación Steinhaus-Moser , es aproximadamente igual a 10[10[4]257]10, los últimos cuatro dígitos son... 1056.
- Matemáticas: Número de Graham , cuyos últimos diez dígitos son... 2464195387. Surge como una solución de límite superior para un problema de la teoría de Ramsey . La representación en potencias de 10 sería poco práctica (la cantidad de 10 en la torre de energía sería prácticamente indistinguible del número en sí).
- Matemáticas: TREE(3) : aparece en relación con un teorema sobre árboles en la teoría de grafos . La representación del número es difícil, pero un límite inferior débil es A A (187196) (1), donde A(n) es una versión de la función de Ackermann .
- Matemáticas: SSCG(3) : aparece en relación con el teorema de Robertson-Seymour . Se sabe que es mayor que TREE(3).
- Matemáticas: Enteros trascendentales: un conjunto de números definidos en 2000 por Harvey Friedman , aparece en la teoría de la prueba. [86]
- Matemáticas: El número de Rayo es un número grande que lleva el nombre de Agustín Rayo y que se ha afirmado que es el número más grande que jamás se haya nombrado. [87] Se definió originalmente en un "duelo de números grandes" en el MIT el 26 de enero de 2007. [88]
Véase también
- Notación de flecha encadenada de Conway
- Comparaciones de tamaño enciclopédico en Wikipedia
- Jerarquía de rápido crecimiento
- Sistema de numeración indio
- Infinidad
- Grandes números
- Lista de números
- Constante matemática
- Nombres de números grandes
- Nombres de números pequeños
- Potencia de 10
Referencias
- ^ Charles Kittel y Herbert Kroemer (1980). Física térmica (2.ª ed.) . WH Freeman Company. pág. 53. ISBN 978-0-7167-1088-2.
- ^ Hay alrededor de 130.000 letras y 199.749 caracteres en total en Hamlet ; 26 letras ×2 para mayúsculas, 12 para caracteres de puntuación = 64, 64 199749 ≈ 10 360.783 .
- ^ Calculado: 365! / 365 365 ≈ 1,455 × 10−157
- ^ Robert Matthews. "¿Cuáles son las probabilidades de barajar una baraja de cartas en el orden correcto?". Science Focus . Consultado el 10 de diciembre de 2018 .
- ^ www.BridgeHands.com, Ventas. "Probabilidades varias: probabilidades del bridge". Archivado desde el original el 3 de octubre de 2009.
- ^ Wilco, Daniel (16 de marzo de 2023). "Las probabilidades absurdas de un cuadro perfecto de la NCAA". NCAA.com . Consultado el 16 de abril de 2023 .
- ^ Walraven, PL; Lebeek, HJ (1963). "Sensibilidad foveal del ojo humano en el infrarrojo cercano". J. Opt. Soc. Am . 53 (6): 765–766. Bibcode :1963JOSA...53..765W. doi :10.1364/josa.53.000765. PMID 13998626.
- ^ Courtney Taylor. "La probabilidad de recibir una escalera real en el póquer". ThoughtCo . Consultado el 10 de diciembre de 2018 .
- ^ Mason, WS; Seal, G; Summers, J (1980-12-01). "Virus de los patos de Pekín con relación estructural y biológica al virus de la hepatitis B humana". Journal of Virology . 36 (3): 829–836. doi :10.1128/JVI.36.3.829-836.1980. ISSN 0022-538X. PMC 353710 . PMID 7463557.
- ^ "Mariposas". Instituto Smithsoniano . Consultado el 27 de noviembre de 2020 .
- ^ ab "Homo sapiens – Ensembl genome browser 87". www.ensembl.org . Archivado desde el original el 25 de mayo de 2017 . Consultado el 28 de enero de 2017 .
- ^ "Lista de clasificación mundial de Pi". Archivado desde el original el 29 de junio de 2017.
- ^ Sloane, N. J. A. (ed.). "Secuencia A360000". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 14 de abril de 2023 .
- ^ "El informe de Kew hace un nuevo recuento del número de plantas del mundo". BBC News . 2016-05-09 . Consultado el 2020-11-27 .
- ^ "Se estima que se eliminarán 600.000 especies de plantas con flores". phys.org . Consultado el 28 de noviembre de 2020 .
- ^ Jacob. "¿Cuántos videojuegos existen?". Gaming Shift . Consultado el 28 de noviembre de 2020 .
- ^ Kibrik, AE (2001). "Archi (caucásico—daguestaní)", The Handbook of Morphology , Blackwell, pág. 468
- ^ Judd DB, Wyszecki G (1975). Color in Business, Science and Industry (El color en los negocios, la ciencia y la industria) . Serie Wiley en Óptica pura y aplicada (tercera edición). Nueva York: Wiley-Interscience . pág. 388. ISBN 978-0-471-45212-6.
- ^ Queen, Tim (26 de marzo de 2022). "¿Cuántos canales de YouTube hay?". Tim Queen . Consultado el 28 de marzo de 2022 .
- ^ El inversor de Plouffe Archivado el 12 de agosto de 2005 en Wayback Machine.
- ^ "¿Cuántos coches hay en el mundo?". carsguide . 6 de agosto de 2018 . Consultado el 18 de mayo de 2020 .
- ^ Master, Farah (17 de enero de 2024). "La población de China cae por segundo año, con una tasa de natalidad históricamente baja". Reuters . Consultado el 17 de enero de 2024 .
- ^ "Perspectivas de población mundial – División de población – Naciones Unidas". population.un.org . Consultado el 2 de julio de 2023 .
- ^ "¿Cuántas cuentas de usuario de Gmail hay en el mundo? | blog.gsmart.in" . Consultado el 28 de noviembre de 2020 .
- ^ Christof Baron (2015). "Usuarios de Facebook en todo el mundo en 2016 | Statista". Statista . statista.com. Archivado desde el original el 9 de septiembre de 2016.
- ^ "La Oficina del Censo proyecta las poblaciones de Estados Unidos y del mundo el día de Año Nuevo". commerce.gov . 3 de enero de 2024 . Consultado el 2 de junio de 2024 .
- ^ ab "Microbios terrestres en la Luna". Science@Nasa. 1 de septiembre de 1998. Archivado desde el original el 23 de marzo de 2010. Consultado el 2 de noviembre de 2010 .
- ^ "¿Cuántos planetas hay en la Vía Láctea? | Cantidad, ubicación y datos clave". Los nueve planetas . 29 de septiembre de 2020 . Consultado el 28 de noviembre de 2020 .
- ^ Enero de 2013, Space.com Staff 02 (2 de enero de 2013). «100 mil millones de planetas alienígenas llenan nuestra galaxia, la Vía Láctea: estudio». Space.com . Consultado el 28 de noviembre de 2020 .
{{cite web}}: CS1 maint: numeric names: authors list (link) - ^ "hasta 2009 no existía, según nuestro conocimiento, una estimación directa y real del número de células o neuronas en todo el cerebro humano que se pudiera citar. Williams y Herrup (1988) proporcionaron una aproximación razonable a partir de la recopilación de números parciales en la literatura. Estos autores estimaron el número de neuronas en el cerebro humano en unos 85 mil millones [...] Sin embargo, con estimaciones más recientes de 21-26 mil millones de neuronas en la corteza cerebral (Pelvig et al., 2008) y 101 mil millones de neuronas en el cerebelo (Andersen et al., 1992), el número total de neuronas en el cerebro humano aumentaría a más de 120 mil millones de neuronas". Herculano-Houzel, Suzana (2009). "El cerebro humano en números: un cerebro de primate escalado linealmente". Front. Hum. Neurosci . 3 : 31. doi : 10.3389/neuro.09.031.2009 . PMC 2776484. PMID 19915731 .
- ^ "Dosis de plaquetas, indicaciones, interacciones, efectos adversos y más". reference.medscape.com . Consultado el 31 de octubre de 2022 .
- ^ Kapitsa, Sergei P (1996). "La teoría fenomenológica del crecimiento de la población mundial". Physics-Uspekhi . 39 (1): 57–71. Bibcode :1996PhyU...39...57K. doi :10.1070/pu1996v039n01abeh000127. S2CID 250877833.(citando el rango de 80 a 150 mil millones, citando a KM Weiss, Human Biology 56637, 1984, y N. Keyfitz, Applied Mathematical Demography, Nueva York: Wiley, 1977). C. Haub, "How Many People Have Ever Lived on Earth?", Population Today 23.2), pp. 5-6, citó una estimación de 105 mil millones de nacimientos desde 50.000 a. C., actualizada a 107 mil millones a partir de 2011 en Haub, Carl (octubre de 2011). "How Many People Have Ever Lived on Earth?". Population Reference Bureau . Archivado desde el original el 24 de abril de 2013. Consultado el 29 de abril de 2013 .(debido a la alta mortalidad infantil en tiempos premodernos, cerca de la mitad de este número no habría vivido más allá de la infancia).
- ^ Elizabeth Howell, ¿Cuántas estrellas hay en la Vía Láctea? Archivado el 28 de mayo de 2016 en Wayback Machine , Space.com, 21 de mayo de 2014 (se citan estimaciones que van desde 100 a 400 mil millones).
- ^ "Carreras de números primos" (PDF) . granville.dvi . Consultado el 4 de enero de 2024 .
- ^ Hollis, Morgan (13 de octubre de 2016). «Un universo de dos billones de galaxias». The Royal Astronomical Society . Consultado el 9 de noviembre de 2017 .
- ^ Jonathan Amos (3 de septiembre de 2015). «Los árboles de la Tierra suman 'tres billones'». BBC. Archivado desde el original el 6 de junio de 2017.
- ↑ Xavier Gourdon (octubre de 2004). «Cálculo de ceros de la función Zeta». Archivado desde el original el 15 de enero de 2011. Consultado el 2 de noviembre de 2010 .
- ^ Haruka Iwao, Emma (14 de marzo de 2019). «Pi en el cielo: cálculo de un número récord de 31,4 billones de dígitos de la constante de Arquímedes en Google Cloud». Archivado desde el original el 19 de octubre de 2019. Consultado el 12 de abril de 2019 .
- ^ Koch, Christof. Biofísica de la computación: procesamiento de información en neuronas individuales. Oxford University Press, 2004.
- ^ Savage, DC (1977). "Ecología microbiana del tracto gastrointestinal". Revisión anual de microbiología . 31 : 107–33. doi :10.1146/annurev.mi.31.100177.000543. PMID 334036.
- ^ Berg, R. (1996). "La microflora gastrointestinal indígena". Tendencias en microbiología . 4 (11): 430–5. doi :10.1016/0966-842X(96)10057-3. PMID 8950812.
- ^ abc Sloane, N. J. A. (ed.). "Secuencia A186311 (menos del siglo 100k al 100k+99 con exactamente n primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 16 de junio de 2023 .
- ^ Bert Holldobler y EO Wilson El superorganismo: la belleza, la elegancia y la extrañeza de las sociedades de insectos Nueva York:2009 WW Norton Página 5
- ^ Silva, Tomás Oliveira e. "Verificación de la conjetura de Goldbach" . Consultado el 11 de abril de 2021 .
- ^ "60º aniversario de la industria de la microelectrónica". Asociación de la Industria de Semiconductores. 13 de diciembre de 2007. Archivado desde el original el 13 de octubre de 2008. Consultado el 2 de noviembre de 2010 .
- ^ Secuencia A131646 Archivado el 1 de septiembre de 2011 en Wayback Machine en La enciclopedia en línea de secuencias de números enteros
- ^ "Enciclopedia Smithsonian: Número de insectos Archivado el 28 de diciembre de 2016 en Wayback Machine ". Preparado por el Departamento de Biología Sistemática, Sección de Entomología, Museo Nacional de Historia Natural , en cooperación con los Servicios de Consulta Pública, Institución Smithsonian . Consultado el 27 de diciembre de 2016. Datos sobre el número de insectos. Calcula el número de insectos individuales en la Tierra en aproximadamente 10 quintillones (10 19 ).
- ^ Ivan Moscovich , 1000 juegos: rompecabezas, paradojas, ilusiones y juegos , Workman Pub., 2001 ISBN 0-7611-1826-8 .
- ^ "Decenas de granjas de Zimbabwe 'incautadas'". BBC . 23 de febrero de 2009. Archivado desde el original el 1 de marzo de 2009 . Consultado el 14 de marzo de 2009 .
- ^ "Ver el Universo en un Grano de Arena de Taranaki". Archivado desde el original el 30 de junio de 2012.
- ^ "Intel predice que habrá 1.200 trillones de transistores en el mundo para 2015". Archivado desde el original el 5 de abril de 2013.
- ^ "¿Cuántos transistores se han enviado alguna vez? – Forbes". Forbes . Archivado desde el original el 30 de junio de 2015 . Consultado el 1 de septiembre de 2015 .
- ^ "Enumeración de sudokus". Archivado desde el original el 6 de octubre de 2006.
- ^ "Recuento de estrellas: un astrónomo de la ANU logra el mejor resultado hasta ahora". The Australian National University. 17 de julio de 2003. Archivado desde el original el 24 de julio de 2005. Consultado el 2 de noviembre de 2010 .
- ^ "Los astrónomos cuentan las estrellas". BBC News. 22 de julio de 2003. Archivado desde el original el 13 de agosto de 2006. Consultado el 18 de julio de 2006 ."billones de tierras podrían estar orbitando alrededor de 300 sextillones de estrellas" van Dokkum, Pieter G.; Charlie Conroy (2010). "Una población sustancial de estrellas de baja masa en galaxias elípticas luminosas". Nature . 468 (7326): 940–942. arXiv : 1009.5992 . Bibcode :2010Natur.468..940V. doi :10.1038/nature09578. PMID 21124316. S2CID 205222998."¿Cuántas estrellas?" Archivado el 22 de enero de 2013 en Wayback Machine ; ver masa del universo observable
- ^ (secuencia A007377 en la OEIS )
- ^ "Preguntas y respuestas: ¿Cuántos átomos hay en el cuerpo humano?". Archivado desde el original el 6 de octubre de 2003.
- ^ William B. Whitman; David C. Coleman; William J. Wiebe (1998). "Procariotas: la mayoría invisible". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 95 (12): 6578–6583. Bibcode :1998PNAS...95.6578W. doi : 10.1073/pnas.95.12.6578 . PMC 33863 . PMID 9618454.
- ^ (secuencia A070177 en la OEIS )
- ^ (secuencia A035064 en la OEIS )
- ^ John Tromp (2010). "El patio de juegos de ajedrez de John". Archivado desde el original el 1 de junio de 2014.
- ^ ab Merickel, James G. (ed.). "Secuencia A217379 (Números que tienen una potencia no pandigital del tamaño de registro (excluye múltiplos de 10).)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 17 de marzo de 2021 .
- ^ Colaboración Planck (2016). "Resultados de Planck 2015. XIII. Parámetros cosmológicos (véase la Tabla 4 en la página 31 de pfd)". Astronomía y Astrofísica . 594 : A13. arXiv : 1502.01589 . Código Bibliográfico :2016A&A...594A..13P. doi :10.1051/0004-6361/201525830. S2CID 119262962.
- ^ Paul Zimmermann , "Los 50 factores más importantes encontrados por ECM Archivado el 20 de febrero de 2009 en Wayback Machine ".
- ^ Matthew Champion, "Re: ¿Cuántos átomos componen el universo?" Archivado el 11 de mayo de 2012 en Wayback Machine , 1998
- ^ WMAP- Contenido del Universo Archivado el 26 de julio de 2016 en Wayback Machine . Map.gsfc.nasa.gov (16 de abril de 2010). Consultado el 1 de mayo de 2011.
- ^ "Nombres de números grandes y pequeños". bmanolov.free.fr . Páginas misceláneas de Borislav Manolov. Archivado desde el original el 30 de septiembre de 2016.
- ^ Hanke, Steve; Krus, Nicholas. "Tabla de hiperinflación" (PDF) . Consultado el 26 de marzo de 2021 .
- ^ "Richard Eldridge".
- ^ Chris Caldwell, Los veinte mejores: prueba de primalidad de la curva elíptica en The Prime Pages .
- ^ Chris Caldwell, Los veinte mejores: Sophie Germain (p) en The Prime Pages .
- ^ Chris Caldwell, Los veinte mejores: Twin en The Prime Pages .
- ^ Chris Caldwell, Los veinte mejores: Primorial en The Prime Pages .
- ^ Del tercer párrafo del relato se desprende: «Cada libro contiene 410 páginas; cada página, 40 líneas; cada línea, unas 80 letras negras». Eso da 410 x 40 x 80 = 1.312.000 caracteres. El quinto párrafo nos dice que «hay 25 símbolos ortográficos», incluidos los espacios y la puntuación. La magnitud del número resultante se encuentra tomando logaritmos. Sin embargo, este cálculo sólo da un límite inferior para el número de libros, ya que no tiene en cuenta las variaciones en los títulos; el narrador no especifica un límite para el número de caracteres en el lomo. Para una discusión más amplia sobre este tema, véase Bloch, William Goldbloom. The Unimaginable Mathematics of Borges' Library of Babel . Oxford University Press: Oxford, 2008.
- ^ Chris Caldwell, Los veinte mejores: Palíndromo en The Prime Pages .
- ^ Gary Barnes, Conjeturas y pruebas de Riesel Archivado el 12 de abril de 2021 en Wayback Machine.
- ^ Chris Caldwell, Los veinte mejores: números primos factoriales Archivado el 10 de abril de 2013 en Wayback Machine en The Prime Pages .
- ^ Chris Caldwell, Los veinte mejores: Fermat generalizado Archivado el 28 de marzo de 2021 en Wayback Machine en The Prime Pages .
- ^ Registros PRP
- ^ Chris Caldwell, Los veinte mejores: Proth Archivado el 24 de noviembre de 2020 en Wayback Machine en The Prime Pages .
- ^ por Chris Caldwell, Los veinte primeros: los primos más grandes conocidos en The Prime Pages .
- ^ Chris Caldwell, Primos de Mersenne: Historia, teoremas y listas en The Prime Pages .
- ^ asantos (15 de diciembre de 2007). «Googol y Googolplex de Carl Sagan». Archivado desde el original el 12 de diciembre de 2021, vía YouTube.
- ^ Zyga, Lisa "Los físicos calculan el número de universos paralelos" Archivado el 6 de junio de 2011 en Wayback Machine . , PhysOrg , 16 de octubre de 2009.
- ^ Don N. Page para la Universidad de Cornell (2007). "El desafío de Susskind a la propuesta de no-límite de Hartle-Hawking y posibles resoluciones". Journal of Cosmology and Astroparticle Physics . 2007 (1): 004. arXiv : hep-th/0610199 . Bibcode :2007JCAP...01..004P. doi :10.1088/1475-7516/2007/01/004. S2CID 17403084.
- ^ H. Friedman, Enormes números enteros en la vida real (consultado el 6 de febrero de 2021)
- ^ "El número de CH. Rayo". The Math Factor Podcast . Consultado el 24 de marzo de 2014 .
- ^ Kerr, Josh (7 de diciembre de 2013). «Concurso de acertar el número más grande». Archivado desde el original el 20 de marzo de 2016. Consultado el 27 de marzo de 2014 .
Enlaces externos
- El artículo de Seth Lloyd , Capacidad computacional del universo, proporciona una serie de interesantes cantidades adimensionales.
- Propiedades notables de números específicos
- Clewett, James. «4.294.967.296 – Internet está llena». Numberphile . Brady Haran . Archivado desde el original el 24 de mayo de 2013 . Consultado el 6 de abril de 2013 .




















