Temperamento igual

Comparación de algunos temperamentos iguales. ^[a] El gráfico abarca una octava horizontalmente (abra la imagen para ver el ancho completo) y cada rectángulo sombreado tiene el ancho de un paso en una escala. Las proporciones de intervalos justos están separadas en filas por sus límites primos .

Un temperamento igual es un temperamento musical o sistema de afinación que se aproxima a intervalos dividiendo una octava (u otro intervalo) en pasos de manera que la relación de las frecuencias de cualquier par de notas adyacentes sea la misma. Este sistema produce pasos de tono que se perciben como de igual tamaño, debido a los cambios logarítmicos en la frecuencia del tono. ^[2]

En la música clásica y en la música occidental en general, el sistema de afinación más común desde el siglo XVIII ha sido el temperamento igual de 12 (también conocido como temperamento igual de 12 tonos , 12 TET o 12 ET , abreviado informalmente como 12 igual ) , que divide la octava en 12 partes, todas las cuales son iguales en una escala logarítmica , con una razón igual a la raíz 12 de 2, (  ¹² √ 2 ≈ 1.05946). Ese intervalo más pequeño resultante,1/12⁠ el ancho de una octava, se llama semitono o medio paso. En los países occidentales el término temperamento igual , sin calificación, generalmente significa 12 TET .

En la actualidad, el 12 TET suele estar afinado en relación con un tono estándar de 440 Hz, llamado A 440 , lo que significa que una nota, A , está afinada a 440  hercios y todas las demás notas se definen como un múltiplo de semitonos de distancia de ella, ya sea más alta o más baja en frecuencia. El tono estándar no siempre ha sido 440 Hz; ha variado considerablemente y, en general, ha aumentado en los últimos cientos de años. ^[3]

Otros temperamentos iguales dividen la octava de forma diferente. Por ejemplo, algunas piezas musicales se han escrito en 19 TET y 31 TET , mientras que el sistema tonal árabe utiliza 24 TET .

En lugar de dividir una octava, un temperamento igual también puede dividir un intervalo diferente, como la versión de temperamento igual de la escala de Bohlen-Pierce , que divide el intervalo justo de una octava y una quinta (relación 3:1), llamado "tritava" o " pseudooctava " en ese sistema, en 13 partes iguales.

Para los sistemas de afinación que dividen la octava equitativamente, pero que no son aproximaciones de solo intervalos, se puede utilizar el término división equitativa de la octava , o EDO .

Los conjuntos de cuerdas sin trastes , que pueden ajustar la afinación de todas las notas excepto las cuerdas al aire , y los grupos vocales, que no tienen limitaciones de afinación mecánica, a veces usan una afinación mucho más cercana a la entonación justa por razones acústicas. Otros instrumentos, como algunos instrumentos de viento , teclado y trastes , a menudo solo se aproximan al temperamento igual, donde las limitaciones técnicas impiden afinaciones exactas. ^[4] Algunos instrumentos de viento que pueden doblar su tono fácil y espontáneamente, sobre todo los trombones , usan una afinación similar a los conjuntos de cuerdas y los grupos vocales.

Una comparación de temperamentos iguales entre 10 TET y 60 TET en cada intervalo principal de límites primos pequeños (rojo: ⁠3/ 2 ⁠ , verde: ⁠5/ 4 ⁠ , índigo: ⁠7/ 4 ⁠ , amarillo: ⁠11/ 8 ⁠ , cian: ⁠13/ 8 ⁠ ). Cada gráfico coloreado muestra cuánto error ocurre (en centavos) en la aproximación más cercana del intervalo justo correspondiente (la línea negra en el centro). Dos curvas negras que rodean el gráfico en ambos lados representan el error máximo posible, mientras que las grises dentro de ellas indican la mitad del mismo.

Esta sección no cita ninguna fuente . Por favor, ayude a mejorar esta sección añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado . ( Junio ​​de 2011 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En un temperamento igual, la distancia entre dos pasos adyacentes de la escala es el mismo intervalo . Debido a que la identidad percibida de un intervalo depende de su razón , esta escala en pasos pares es una secuencia geométrica de multiplicaciones. (Una secuencia aritmética de intervalos no sonaría uniformemente espaciada y no permitiría la transposición a diferentes tonalidades ). En concreto, el intervalo más pequeño en una escala de temperamento igual es la razón:

${\displaystyle \ r^{n}=p\ }$

${\displaystyle \ r={\sqrt[{n}]{p\ }}\ }$

donde la relación r divide la relación p (normalmente la octava, que es 2:1) en n partes iguales. ( Véase el temperamento igual de doce tonos más abajo ) .

Las escalas se miden a menudo en centésimas , que dividen la octava en 1200 intervalos iguales (cada uno llamado centésima). Esta escala logarítmica hace que la comparación de diferentes sistemas de afinación sea más fácil que la comparación de proporciones, y tiene un uso considerable en etnomusicología . El paso básico en centésimas para cualquier temperamento igual se puede encontrar tomando el ancho de p arriba en centésimas (generalmente la octava, que tiene 1200 centésimas de ancho), llamado abajo w , y dividiéndolo en n partes:

${\displaystyle \c={\frac {\ w\ }{n}}\ }$

En el análisis musical, el material perteneciente a un temperamento igual se suele representar con una notación entera , lo que significa que se utiliza un único número entero para representar cada tono. Esto simplifica y generaliza la discusión del material de tono dentro del temperamento de la misma manera que tomar el logaritmo de una multiplicación lo reduce a una suma. Además, al aplicar la aritmética modular donde el módulo es el número de divisiones de la octava (normalmente 12), estos números enteros se pueden reducir a clases de tono , lo que elimina la distinción (o reconoce la similitud) entre tonos del mismo nombre, por ejemplo, c es 0 independientemente del registro de octava. El estándar de codificación MIDI utiliza designaciones de notas enteras.

En esta sección falta información sobre las fórmulas generales para el intervalo de temperamento igual. Amplíe la sección para incluir esta información. Puede que existan más detalles en la página de discusión . ( febrero de 2019 )

El temperamento igual de 12 tonos, que divide la octava en 12 intervalos de igual tamaño, es el sistema musical más utilizado hoy en día, especialmente en la música occidental.

Las dos figuras a las que frecuentemente se les atribuye el logro del cálculo exacto del temperamento igual son Zhu Zaiyu (también romanizado como Chu-Tsaiyu. Chino:朱載堉) en 1584 y Simon Stevin en 1585. Según FA Kuttner, un crítico de dar crédito a Zhu, ^[5] se sabe que Zhu "presentó un método altamente preciso, simple e ingenioso para el cálculo aritmético de mono-acordes de temperamento igual en 1584" y que Stevin "ofreció una definición matemática del temperamento igual más un cálculo algo menos preciso de los valores numéricos correspondientes en 1585 o más tarde".

Los acontecimientos se produjeron de forma independiente. ^{[6] (p200)}

Kenneth Robinson atribuye la invención del temperamento igual a Zhu ^{[7] [b]} y proporciona citas textuales como evidencia. ^[8] En 1584 Zhu escribió:

He fundado un nuevo sistema. Establezco un pie como el número del que se deben extraer los demás y, utilizando proporciones, los extraigo. En total, hay que encontrar las cifras exactas de los flautistas en doce operaciones. ^{[9] [8]}

Kuttner no está de acuerdo y señala que su afirmación "no puede considerarse correcta sin mayores reservas". ^[5] Kuttner propone que ni Zhu ni Stevin alcanzaron el temperamento igual y que ninguno de ellos debería ser considerado su inventor. ^[10]

Los teóricos chinos ya habían elaborado aproximaciones para el temperamento igual de 12 tonos , pero Zhu fue la primera persona en resolver matemáticamente el temperamento igual de 12 tonos, ^[11] que describió en dos libros, publicados en 1580 ^[12] y 1584. ^{[9] [13]} Needham también ofrece una explicación ampliada. ^[14]

Zhu obtuvo su resultado dividiendo la longitud de la cuerda y el tubo sucesivamente por ¹² √ 2  ≈ 1.059463 , y para la longitud del tubo por ²⁴ √ 2  ≈ 1.029302 , ^[15] de modo que después de 12 divisiones (una octava), la longitud se redujo a la mitad.

Zhu creó varios instrumentos afinados según su sistema, incluidas flautas de bambú. ^[16]

Algunos de los primeros europeos que defendieron el temperamento igual fueron los laudistas Vincenzo Galilei , Giacomo Gorzanis y Francesco Spinacino , quienes escribieron música en él. ^{[17] [18] [19] [20]}

Simon Stevin fue el primero en desarrollar  la TTE 12 basándose en la raíz duodécima de dos , que describió en van de Spiegheling der singconst ( c.  1605 ), publicado póstumamente en 1884. ^[21]

Los intérpretes de instrumentos de cuerda pulsada (laudistas y guitarristas) generalmente favorecían el temperamento igual, ^[22] mientras que otros estaban más divididos. ^[23] Al final, el temperamento igual de 12 tonos ganó. Esto permitió que la modulación enarmónica , nuevos estilos de tonalidad simétrica y politonalidad , música atonal como la escrita con la técnica de 12 tonos o serialismo , y el jazz (al menos su componente de piano) se desarrollaran y florecieran.

En el temperamento igual de 12 tonos, que divide la octava en 12 partes iguales, el ancho de un semitono , es decir, la relación de frecuencias del intervalo entre dos notas adyacentes, es la raíz duodécima de dos :

${\displaystyle {\sqrt[{12}]{2\ }}=2^{\tfrac {1}{12}}\aproximadamente 1.059463}$

Este intervalo se divide en 100 céntimos.

Para encontrar la frecuencia, P _n , de una nota en 12  TET , se puede utilizar la siguiente fórmula:

${\displaystyle \ P_{n}=P_{a}\ \cdot \ {\Bigl (}\ {\sqrt[{12}]{2\ }}\ {\Bigr )}^{na}\ }$

En esta fórmula, P _n representa el tono o la frecuencia (normalmente en hercios ) que estás intentando encontrar. P _a es la frecuencia de un tono de referencia. Los números índices n y a son las etiquetas asignadas al tono deseado ( n ) y al tono de referencia ( a ). Estos dos números proceden de una lista de números enteros consecutivos asignados a semitonos consecutivos. Por ejemplo, A ₄ (el tono de referencia) es la 49.ª tecla desde el extremo izquierdo de un piano (afinado a 440 Hz ), y C ₄ ( do central ) y F ♯ ₄ son las teclas 40.ª y 46.ª, respectivamente. Estos números se pueden utilizar para encontrar la frecuencia de C ₄ y F ♯ ₄ :

${\displaystyle P_{40}=440\ {\mathsf {Hz}}\ \cdot \ {\Bigl (}{\sqrt[{12}]{2}}\ {\Bigr )}^{(40-49)}\aproximadamente 261,626\ {\mathsf {Hz}}\ }$

${\displaystyle P_{46}=440\ {\mathsf {Hz}}\ \cdot \ {\Bigl (}{\sqrt[{12}]{2}}\ {\Bigr )}^{(46-49)}\aproximadamente 369,994\ {\mathsf {Hz}}\ }$

Para convertir una frecuencia (en Hz) a su contraparte equivalente 12  TET , se puede utilizar la siguiente fórmula:

${\displaystyle \ E_{n}=E_{a}\ \cdot \ 2^{\ x}\ \quad }$donde en general${\displaystyle \quad \ x\ \equiv \ {\frac {1}{\ 12\ }}\ \operatorname {round} \!{\Biggl (}12\log _{2}\left({\frac {\ n\ }{a}}\right){\Biggr )}~.}$

E _n es la frecuencia de un tono en temperamento igual y E _a es la frecuencia de un tono de referencia. Por ejemplo, si hacemos que el tono de referencia sea igual a 440 Hz, podemos ver que E ₅ y C ♯ ₅ tienen las siguientes frecuencias, respectivamente:

${\displaystyle E_{660}=440\ {\mathsf {Hz}}\ \cdot \ 2^{\left({\frac {7}{\ 12\ }}\right)}\ \aproximadamente \ 659,255\ {\mathsf {Hz}}\ \quad }$donde en este caso${\displaystyle \quad x={\frac {1}{\ 12\ }}\ \operatorname {round} \!{\Biggl (}\ 12\log _{2}\left({\frac {\ 660\ }{440}}\right)\ {\Biggr )}={\frac {7}{\ 12\ }}~.}$

${\displaystyle E_{550}=440\ {\mathsf {Hz}}\ \cdot \ 2^{\left({\frac {1}{\ 3\ }}\right)}\ \aproximadamente \ 554,365\ {\mathsf {Hz}}\ \quad }$ donde en este caso${\displaystyle \quad x={\frac {1}{\ 12\ }}\ \operatorname {round} \!{\Biggl (}12\log _{2}\left({\frac {\ 550\ }{440}}\right){\Biggr )}={\frac {4}{\ 12\ }}={\frac {1}{\ 3\ }}~.}$

Los intervalos de 12  TET se aproximan mucho a algunos intervalos en entonación justa . ^[24] Las quintas y cuartas están casi indistinguiblemente cerca de los intervalos justos, mientras que las terceras y sextas están más alejadas.

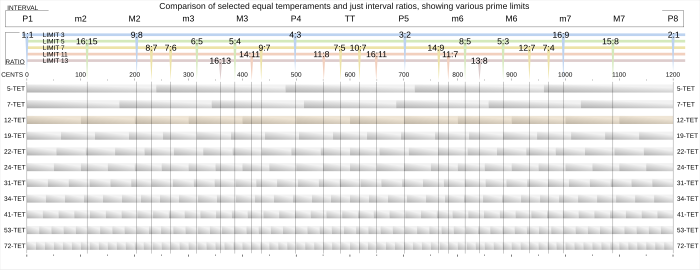
En la siguiente tabla se comparan los tamaños de varios intervalos justos con sus contrapartes de temperamento igual, expresados ​​como una proporción y en centavos.

Nombre del intervalo	Valor exacto en 12  TET	Valor decimal en 12  TET	Empezar	Intervalo de entonación justo	Céntimos en entonación justa	Error de afinación de 12  centavos TET
Unísono ( C )	2 0 ⁄ 12 = 1	1	0	⁠1/1⁠ = 1	0	0
Segunda menor ( D ♭ )	2 1 ⁄ 12 = 12 √ 2	1.059463	100	⁠16/15⁠ = 1.06666...	111,73	-11,73
Segunda mayor ( D )	2 2 ⁄ 12 = 6 √ 2	1.122462	200	⁠9/8⁠ = 1,125	203,91	-3,91
Tercera menor ( Mi ♭ )	2 3 ⁄ 12 = 4 √ 2	1.189207	300	⁠6/5⁠ = 1,2	315,64	-15,64
Tercera mayor ( Mi )	2 4 ⁄ 12 = 3 √ 2	1.259921	400	⁠5/4⁠ = 1,25	386.31	+13,69
Cuarta perfecta ( F )	2 5 ⁄ 12 = 12 √ 32	1.33484	500	⁠4/3⁠ = 1,33333...	498.04	+1,96
Tritono ( G ♭ )	2 6 ⁄ 12 = √ 2	1.414214	600	⁠64/45⁠ = 1,42222...	609,78	-9,78
Quinta perfecta ( G )	2 7 ⁄ 12 = 12 √ 128	1.498307	700	⁠3/2⁠ = 1,5	701,96	-1,96
Sexta menor ( La ♭ )	2 8 ⁄ 12 = 3 √ 4	1.587401	800	⁠8/5⁠ = 1,6	813,69	-13,69
Sexta mayor ( La )	2 9 ⁄ 12 = 4 √ 8	1.681793	900	⁠5/3⁠ = 1.66666...	884.36	+15,64
Séptima menor ( si ♭ )	2 10 ⁄ 12 = 6 √ 32	1.781797	1000	⁠16/9⁠ = 1,77777...	996.09	+3,91
Séptima mayor ( B )	2 11 ⁄ 12 = 12 √ 2048	1.887749	1100	⁠15/8⁠ = 1,875	1088.270	+11,73
Octava ( C )	2 12 ⁄ 12 = 2	2	1200	⁠2/1⁠ = 2	1200.00	0

Los violines, violas y violonchelos están afinados en quintas perfectas ( GDAE para violines y CGDA para violas y violonchelos), lo que sugiere que su proporción de semitonos es ligeramente mayor que en el temperamento igual convencional de 12 tonos. Debido a que una quinta perfecta está en una relación de 3:2 con su tono base, y este intervalo comprende siete pasos, cada tono está en una proporción de ⁷ √ ⁠3/2⁠ al siguiente (100,28 cents), lo que proporciona una quinta perfecta con una relación de 3:2, pero una octava ligeramente ensanchada con unarelación de ≈ 517:258 o ≈ 2,00388:1en lugar de la habitual 2:1, porque 12 quintas perfectas no equivalen a siete octavas.^[25]Sin embargo, durante la interpretación real, los violinistas eligen los tonos de oído, y solo se garantiza que los cuatro tonos no tapados de las cuerdas exhiban esta relación de 3:2.

Los temperamentos iguales de cinco y siete tonos ( 5 TET Play ^ⓘ y {{7 TET }} Play ^ⓘ ), con pasos de 240 cent Play ^ⓘ y 171 cent Play ^ⓘ , respectivamente, son bastante comunes.

5 TET y 7 TET marcan los puntos finales del rango de afinación válido del temperamento sintónico , como se muestra en la Figura 1.

• En 5 TET , la quinta perfecta temperada tiene 720 centavos de ancho (en la parte superior del continuo de afinación) y marca el punto final del continuo de afinación en el que el ancho de la segunda menor se reduce a un ancho de 0 centavos.
• En 7 TET , la quinta perfecta temperada tiene 686 centavos de ancho (en la parte inferior del continuo de afinación) y marca el punto final en el continuo de afinación, en el que la segunda menor se expande para ser tan ancha como la segunda mayor (a 171 centavos cada una).

Según Kunst (1949), los gamelanes indonesios están afinados a 5 TET , pero según Hood (1966) y McPhee (1966) su afinación varía ampliamente, y según Tenzer (2000) contienen octavas estiradas . Ahora se acepta que de los dos sistemas de afinación primarios en la música de gamelan, slendro y pelog , solo slendro se parece un poco al temperamento igual de cinco tonos, mientras que pelog es altamente desigual; sin embargo, en 1972 Surjodiningrat, Sudarjana y Susanto analizan pelog como equivalente a 9-TET (pasos de 133 centésimas Play ^ⓘ ). ^[26]

Un xilófono tailandés medido por Morton en 1974 "varió sólo más o menos 5 centavos" de 7 TET . ^[27] Según Morton,

"Los instrumentos tailandeses de tono fijo están afinados en un sistema equidistante de siete tonos por octava... Sin embargo, como en la música tradicional occidental, no todos los tonos del sistema de afinación se utilizan en un modo (a menudo denominado 'escala'); en el sistema tailandés, cinco de los siete se utilizan en tonos principales en cualquier modo, estableciendo así un patrón de intervalos no equidistantes para el modo". ^[28] Reproducir ^ⓘ

Una escala indígena sudamericana de una cultura preinstrumental medida por Boiles en 1969 presentaba un temperamento igual de siete tonos de 175 centésimas, que estira ligeramente la octava, como en la música gamelán instrumental. ^[29]

La música china ha utilizado tradicionalmente 7 TET . ^{[c] [d]}

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (March 2020) (Learn how and when to remove this message)

19 EDO

Se han construido muchos instrumentos utilizando la afinación EDO 19. Equivalente a ⁠ 1 /3⁠ coma mediatonal , tiene una quinta perfecta ligeramente más plana (a 695 centavos), pero su tercera menor y sexta mayor están a menos de una quinta parte de un centavo de distancia de solo, con el EDO más bajo que produce una tercera menor y sexta mayor mejor que 19 EDO siendo 232 EDO. Su cuarta perfecta (a 505 centavos), es siete centavos más aguda que la de la entonación justa y cinco centavos más aguda que la de 12 EDO.

22 EDO

22 EDO es uno de los EDO más precisos para representar el temperamento superpyth (donde 7:4 y 16:9 son el mismo intervalo) y está cerca del generador óptimo para el temperamento puercoespín. Las quintas son tan agudas que las terceras mayores y menores que obtenemos al apilar quintas serán la tercera supermayor (9/7) y la tercera submenor (7/6). Un paso más cerca entre sí están las terceras mayores y menores clásicas (5/4 y 6/5).

23 de diciembre de 1968

23 EDO es el EDO más grande que no logra aproximarse a los armónicos 3.er, 5.º, 7.º y 11.º (3:2, 5:4, 7:4, 11:8) dentro de los 20 centavos, pero sí se aproxima muy bien a algunas proporciones entre ellos (como la tercera menor 6:5), lo que lo hace atractivo para los microtonalistas que buscan un territorio armónico inusual.

24 EDO

24 EDO , la escala de cuartos de tono , es particularmente popular, ya que representa un punto de acceso conveniente para compositores condicionados a las prácticas de notación y tono 12 EDO occidentales estándar que también están interesados ​​​​en la microtonalidad. Debido a que 24 EDO contiene todos los tonos de 12 EDO, los músicos emplean los colores adicionales sin perder ninguna táctica disponible en la armonía de 12 tonos. El hecho de que 24 sea un múltiplo de 12 también hace que 24 EDO sea fácil de lograr instrumentalmente empleando dos instrumentos tradicionales de 12 EDO afinados con un cuarto de tono de diferencia, como dos pianos, lo que también permite que cada intérprete (o un intérprete que toque un piano diferente con cada mano) lea la notación familiar de 12 tonos. Varios compositores, incluido Charles Ives , experimentaron con música para pianos de cuartos de tono. 24 EDO también se aproxima muy bien a los armónicos 11 y 13, a diferencia de 12 EDO.

26 de diciembre

26 es el denominador de un convergente a log ₂ (7), afinando el 7º armónico (7:4) con menos de medio centésimo de error. Aunque es un temperamento de tono medio, es muy plano, con cuatro de sus quintas perfectas produciendo una tercera mayor 17 centésimos más baja (equiparada con la tercera neutra 11:9). 26 EDO tiene dos terceras menores y dos sextas menores y podría ser un temperamento alternativo para la armonía de barbería .

27 EDO

27 es el número más bajo de divisiones iguales de la octava que representa de manera única todos los intervalos que involucran los primeros ocho armónicos. Atenúa la coma septimal pero no la coma sintónica .

29 de diciembre

29 es el número más bajo de divisiones iguales de la octava cuya quinta perfecta está más cerca de ser justa que en 12 EDO, en el que la quinta es 1,5 centésimas sostenidas en lugar de 2 centésimas bemol. Su tercera mayor clásica es aproximadamente tan imprecisa como la de 12 EDO, pero está afinada 14 centésimas bemol en lugar de 14 centésimas sostenidas. También afina los armónicos 7.º, 11.º y 13.º bemoles aproximadamente en la misma cantidad, lo que permite que 29 EDO coincida con intervalos como 7:5, 11:7 y 13:11 con mucha precisión. Cortar los 29 intervalos a la mitad produce 58 EDO , lo que permite errores más bajos para algunos tonos justos.

31 EDO

El 31 EDO fue propuesto por Christiaan Huygens y Adriaan Fokker y representa una rectificación del tono medio de una negra en un temperamento igual. El 31 EDO no tiene una quinta perfecta tan precisa como el 12 EDO (como el 19 EDO), pero sus terceras mayores y sextas menores están a menos de 1 centésima de la justa. También proporciona buenas coincidencias para armónicos hasta el 11, de los cuales el séptimo armónico es particularmente preciso.

34 EDO

34 EDO arroja errores de aproximación totales combinados ligeramente inferiores a 3:2, 5:4, 6:5 y sus inversiones que 31 EDO, a pesar de tener un ajuste ligeramente menos preciso para 5:4. 34 EDO no se aproxima con precisión al séptimo armónico o a las relaciones que involucran 7, y no es un tono medio ya que su quinta es sostenida en lugar de bemol. Permite el tritono de 600 centésimas, ya que 34 es un número par.

41 EDO

41 es el siguiente EDO con una quinta perfecta mejor que 29 EDO y 12 EDO. Su tercera mayor clásica también es más precisa, con solo seis centésimas bemol. No es un temperamento medio, por lo que distingue 10:9 y 9:8, junto con las terceras mayores clásicas y pitagóricas, a diferencia de 31 EDO. Es más preciso en el límite de 13 que 31 EDO.

46 EDO

46 EDO proporciona terceras mayores y quintas perfectas que son ligeramente más agudas que justas, y muchos ^{[ ¿quién? ]} dicen que esto le da a las tríadas mayores un sonido brillante característico. Los armónicos primarios hasta el 17 tienen una precisión de 6 centésimas, y 10:9 y 9:5 están a una quinta parte de centésima de la pureza. Como no es un sistema de tonos medios, distingue 10:9 y 9:8.

53 EDO

53 EDO solo ha tenido un uso ocasional, pero es mejor para aproximarse a las consonancias justas tradicionales que 12, 19 o 31 EDO. Sus quintas perfectas extremadamente precisas lo hacen equivalente a una afinación pitagórica extendida , ya que 53 es el denominador de un convergente a log ₂ (3). Con su ciclo preciso de quintas y paso de coma multipropósito, 53 EDO se ha utilizado en la teoría musical turca . No es un temperamento medio, que pone buenas terceras al alcance de la mano apilando quintas; en cambio, como todos los temperamentos cismáticos , las terceras consonantes están representadas por una cuarta disminuida pitagórica (CF ♭ ), que se alcanza apilando ocho cuartas perfectas. También atempera el kleisma , lo que permite alcanzar su quinta mediante una pila de seis terceras menores (6:5).

58 EDO

El temperamento igual 58 es una duplicación del temperamento 29 EDO, que contiene como temperamento incorporado. Al igual que el 29 EDO, puede coincidir con intervalos como 7:4, 7:5, 11:7 y 13:11 con mucha precisión, así como aproximarse mejor a terceras y sextas.

72 EDO

72 EDO se aproxima bien a muchos intervalos de entonación justa , proporcionando equivalentes casi justos a los armónicos 3.º, 5.º, 7.º y 11.º. 72 EDO ha sido enseñado, escrito e interpretado en la práctica por Joe Maneri y sus estudiantes (cuyas inclinaciones atonales generalmente evitan cualquier referencia a la entonación justa ). Como es un múltiplo de 12, 72 EDO puede considerarse una extensión de 12 EDO, que contiene seis copias de 12 EDO que comienzan en diferentes tonos, tres copias de 24 EDO y dos copias de 36 EDO.

96 EDO

El 96 EDO se aproxima a todos los intervalos dentro de 6,25 centésimas, lo que es apenas distinguible. Como múltiplo óctuple de 12, se puede utilizar plenamente como el 12 EDO común. Ha sido defendido por varios compositores, especialmente Julián Carrillo . ^[34]

Otras divisiones iguales de la octava que han encontrado uso ocasional incluyen 13 EDO, 15 EDO , 17 EDO y 55 EDO.

2, 5, 12, 41, 53, 306, 665 y 15601 son denominadores de los primeros convergentes de log ₂ (3), por lo que 2, 5, 12, 41, 53, 306, 665 y 15601 doceavos (y quintos), al estar en temperamentos iguales correspondientes iguales a un número entero de octavas, son mejores aproximaciones de 2, 5, 12, 41, 53, 306, 665 y 15601 sólo doceavos/quintos que en cualquier temperamento igual con menos tonos. ^{[35] [36]}

1, 2, 3, 5, 7, 12, 29, 41, 53, 200, ... (secuencia A060528 en la OEIS ) es la secuencia de divisiones de octava que proporciona cada vez mejores aproximaciones a la quinta justa. Las secuencias relacionadas que contienen divisiones que se aproximan a otros intervalos justos se enumeran en una nota al pie. ^[e]

La versión temperada de la escala de Bohlen-Pierce consiste en la proporción 3:1 (1902 cents), convencionalmente una quinta perfecta más una octava (es decir, una doceava perfecta), llamada en esta teoría una tritava ( play ^ⓘ ), y dividida en 13 partes iguales. Esto proporciona una correspondencia muy cercana a las proporciones justamente afinadas que consisten solo en números impares. Cada paso es 146,3 cents ( play ^ⓘ ), o ¹³ √ 3 ​​.

Wendy Carlos creó tres temperamentos iguales inusuales después de un estudio exhaustivo de las propiedades de los temperamentos posibles con un tamaño de paso entre 30 y 120 centésimas. Estos se llamaron alfa , beta y gamma . Pueden considerarse divisiones iguales de la quinta perfecta. Cada uno de ellos proporciona una muy buena aproximación de varios intervalos justos. ^[37] Sus tamaños de paso:

• alfa : ⁹ √ ⁠3/2⁠ (78,0 centavos) Reproducir ^ⓘ
• beta : ¹¹ √ ⁠3/2⁠ (63,8 centavos) Reproducir ^ⓘ
• gama : ²⁰ √ ⁠3/2⁠ (35,1 centavos) Reproducir ^ⓘ

Se pueden escuchar alfa y beta en la canción principal del álbum de Carlos de 1986, Beauty in the Beast .

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (August 2017) (Learn how and when to remove this message)

En esta sección, el semitono y el tono entero pueden no tener sus significados habituales en 12 EDO, ya que se analiza cómo se pueden templar de formas diferentes a sus versiones justas para producir las relaciones deseadas. Sea s el número de pasos de un semitono y t el número de pasos de un tono .

Existe exactamente una familia de temperamentos iguales que fija el semitono a cualquier fracción propia de un tono entero, manteniendo las notas en el orden correcto (lo que significa que, por ejemplo, C , D , E , F y F ♯ están en orden ascendente si conservan sus relaciones habituales con C ). Es decir, fijar q a una fracción propia en la relación qt = s también define una familia única de un temperamento igual y sus múltiplos que cumplen esta relación.

Por ejemplo, donde k es un número entero, 12 k EDO establece q = ⁠1/2⁠ , 19 k conjuntos EDO q = ⁠1/3⁠ ,y31 k conjuntos EDO q = ⁠ 2 /5⁠ .Los múltiplos más pequeños de estas familias (por ejemplo, 12, 19 y 31 anteriores) tienen la propiedad adicional de no tener notas fuera delcírculo de quintas. (Esto no es cierto en general; en 24  EDO , los semisostenidos y semibemoles no están en el círculo de quintas generado a partir de C ). Los casos extremos son5 k EDO ,donde q = 0 y el semitono se convierte en unísono, y7 k EDO , donde q = 1 y el semitono y el tono son el mismo intervalo.

Una vez que uno sabe cuántos pasos tiene un semitono y un tono en este temperamento igual, puede encontrar el número de pasos que tiene en la octava. Un temperamento igual con las propiedades anteriores (incluyendo no tener notas fuera del círculo de quintas) divide la octava en 7 pasos t − 2 s y la quinta perfecta en 4 pasos t − s . Si hay notas fuera del círculo de quintas, uno debe multiplicar estos resultados por n , el número de círculos de quintas no superpuestos necesarios para generar todas las notas (por ejemplo, dos en 24  EDO , seis en 72  EDO ). (Uno debe tomar el semitono pequeño para este propósito: 19  EDO tiene dos semitonos, uno es ⁠ 1 /3⁠ tono y el otro ser ⁠ 2 /3⁠ . De manera similar, 31  EDO tiene dos semitonos, uno de los cuales es ⁠ 2 /5⁠ tono y el otro ser ⁠ 3 /5⁠ ).

La más pequeña de estas familias es 12 k EDO y , en particular, 12  EDO es el temperamento igual más pequeño con las propiedades anteriores. Además, hace que el semitono sea exactamente la mitad de un tono entero, la relación más simple posible. Estas son algunas de las razones por las que 12  EDO se ha convertido en el temperamento igual más utilizado. (Otra razón es que 12 EDO es el temperamento igual más pequeño que se aproxima a la armonía límite 5, siendo el siguiente más pequeño 19 EDO).

Cada elección de fracción q para la relación da como resultado exactamente una familia de temperamento igual, pero lo inverso no es cierto: 47  EDO tiene dos semitonos diferentes, donde uno es 1 /7⁠ tono y el otro es ⁠ 8 /9⁠ , que no son complementarios entre sí como en 19  EDO ( ⁠ 1 /3⁠ y ⁠ 2 /3⁠ ). Tomando cada semitono se obtiene una elección diferente de quinta perfecta.

Los sistemas de temperamento igual pueden considerarse en términos del espaciamiento de tres intervalos que se encuentran en la entonación justa , la mayoría de cuyos acordes están armónicamente perfectamente afinados, una buena propiedad que no se logra del todo entre casi todas las notas en casi todos los temperamentos iguales. La mayoría de los acordes justos suenan sorprendentemente consonantes, y la mayoría de los acordes de temperamento igual suenan al menos ligeramente disonantes. En Do mayor, esos tres intervalos son: ^[38]

• el tono mayor T  = ⁠  9 /8⁠  = el intervalo de C:D, F:G y A:B;
• el tono menor t  = ⁠  10 /9⁠  = el intervalo entre D:E y G:A;
• el semitono diatónico s  = ⁠  16 /15⁠  = el intervalo entre E:F y B:C.

Analizar un temperamento igual en términos de cómo modifica o adapta estos tres intervalos proporciona una forma rápida de evaluar qué tan consonantes pueden ser varios acordes en ese temperamento, en función de qué tan distorsionados estén estos intervalos. ^{[38] [f]}

La afinación diatónica en temperamento igual de 12 tonos (12 TET ) se puede generalizar a cualquier afinación diatónica regular que divida la octava como una secuencia de pasos T ts T t T s (o algún desplazamiento circular o "rotación" de la misma). Para que se la llame afinación diatónica regular , cada uno de los dos semitonos (  s  ) debe ser más pequeño que cualquiera de los tonos ( tono mayor ,  T  , y tono menor ,  t  ). La coma κ está implícita como la relación de tamaño entre los tonos mayor y menor: Expresado como frecuencias κ = ⁠   yo / a ⁠ ,o comocentavos κ = T − t .  

Las notas en una afinación diatónica regular están conectadas en una "espiral de quintas" que no se cierra (a diferencia del círculo de quintas en 12 TET ). Comenzando en la subdominante F (en la tonalidad de C ) hay tres quintas perfectas seguidas: F – C , C – G y G – D, cada una compuesta de alguna permutación de los intervalos más pequeños TT ts  . Las tres quintas afinadas son interrumpidas por la quinta grave D – A = T tts ( grave significa "bemol por una coma "), seguida por otra quinta perfecta, E – B , y otra quinta grave, B – F ♯ , y luego reiniciando en los sostenidos con F ♯ – C ♯ ; el mismo patrón se repite a través de las notas sostenidas, luego los dobles sostenidos, y así sucesivamente, indefinidamente. Pero cada octava de notas completamente naturales, completamente sostenidas o completamente doblemente sostenidas se aplana con dos comas con cada transición de notas naturales a sostenidas, o de sostenidas simples a dobles sostenidas, etc. El patrón también es inverso-simétrico en las bemoles: descendiendo por cuartas, el patrón agudiza recíprocamente las notas en dos comas con cada transición de notas naturales a notas bemoles, o de bemoles a dobles bemoles, etc. Si se deja sin modificar, las dos quintas graves en cada bloque de notas completamente naturales, o completamente sostenidas, o completamente bemoles, son intervalos "lobo" : cada una de las quintas graves desafinada por una coma diatónica .    

Puesto que la coma, κ , expande el tono menor t = sc , en el tono mayor , T = sc κ , una octava justa T ts T t T s se puede dividir en una secuencia sc κ sc s sc κ sc sc κ s , (o un desplazamiento circular de la misma) de 7 semitonos diatónicos s , 5 semitonos cromáticos c , y 3  comas κ . Varios temperamentos iguales alteran los tamaños de los intervalos, normalmente separando las tres comas y luego redistribuyendo sus partes en los siete semitonos diatónicos s , o en los cinco semitonos cromáticos c , o en ambos s y c , con alguna proporción fija para cada tipo de semitono.       

La secuencia de intervalos s , c y κ se puede agregar repetidamente a sí misma en una espiral mayor de 12 quintas , y se puede hacer que se conecten en sus extremos más alejados mediante ligeros ajustes en el tamaño de uno o varios de los intervalos, o dejarlas sin modificar con ocasionales quintas menos que perfectas, desafinadas por una coma.

Se pueden entender y analizar varios temperamentos iguales como si se hubieran realizado ajustes en los tamaños y subdividido los tres intervalos:  T  ,  t  y  s  , o con una resolución más fina, sus constituyentes  s  ,  c  y  κ  . Se puede crear un temperamento igual haciendo que los tamaños de los tonos mayores y menores ( T , t ) sean los mismos (por ejemplo, estableciendo κ = 0 , con los otros expandidos para que aún llenen la octava), y ambos semitonos ( s y c ) sean los mismos, entonces resultan 12 semitonos iguales, dos por tono. En 12 TET , el semitono, s , es exactamente la mitad del tamaño de los tonos enteros del mismo tamaño T = t .

Algunos de los tamaños intermedios de tonos y semitonos también pueden generarse en sistemas de temperamento igual, modificando los tamaños de la coma y los semitonos. Se obtiene 7 TET en el límite cuando el tamaño de c y κ tiende a cero, con la octava fija, y 5 TET en el límite cuando s y κ tienden a cero; 12 TET es, por supuesto, el caso en el que s = c y κ = 0. Por ejemplo:   

5 TET y 7 TET

Hay dos casos extremos que enmarcan este marco: cuando s y κ se reducen a cero manteniendo el tamaño de la octava fijo, el resultado es ttttt , un temperamento igual de cinco tonos. A medida que s se hace más grande (y absorbe el espacio que antes se usaba para la coma κ ), con el tiempo los pasos son todos del mismo tamaño, ttttttt , y el resultado es un temperamento igual de siete tonos. Estos dos extremos no se incluyen como afinaciones diatónicas "regulares".

19 de marzo

Si el semitono diatónico se establece con el doble del tamaño del semitono cromático, es decir, s = 2 c (en cents) y κ = 0 , el resultado es 19 TET , con un paso para el semitono cromático c , dos pasos para el semitono diatónico s , tres pasos para los tonos T = t y el número total de pasos  3 T + 2 t + 2 s = 9 + 6 + 4 =  19 pasos. El subsistema de 12 tonos incorporado se aproxima mucho al históricamente importante ⁠    1 /3⁠ sistema coma- significado .

31 de marzo

Si el semitono cromático es dos tercios del tamaño del semitono diatónico, es decir c = ⁠ 2 /3⁠ s ,con κ = 0 ,el resultado es31 TET , con dos pasos para el semitono cromático, tres pasos para el semitono diatónico y cinco pasos para el tono, donde  3 T + 2 t + 2 s = 15 + 10 + 6 =  31 pasos. El subsistema de 12 tonos incorporado se aproxima mucho al históricamente importante ⁠ 1 /4⁠ coma significa uno.

43 TET

Si el semitono cromático tiene tres cuartas partes del tamaño del semitono diatónico, es decir c = ⁠ 3 /4⁠ s ,con κ = 0 ,el resultado es 43 TET, con tres pasos para el semitono cromático, cuatro pasos para el semitono diatónico y siete pasos para el tono, donde  3 T + 2 t + 2 s = 21 + 14 + 8 = 43. El subsistema de 12 tonos incorporado se aproxima mucho a ⁠ 1 /5⁠ coma significa uno.

53 TET

Si el semitono cromático tiene el mismo tamaño que tres comas, c = 3 κ (en centésimas, en frecuencia c = κ ³ ), el diatónico tiene el mismo tamaño que cinco comas, s = 5 κ , eso hace que el tono menor tenga ocho comas t = s + c = 8 κ , y el tono mayor nueve, T = s + c + κ = 9 κ . Por lo tanto,  3 T + 2 t + 2 s = 27 κ + 16 κ + 10 κ = 53 κ para 53 pasos de una coma cada uno. El tamaño de la coma / tamaño del paso es κ = ⁠        1 200 /53⁠  ¢exactamente, o κ = 22,642 ¢ ≈ 21,506 ¢ ,lacoma sintónica. Es una aproximación extremadamente cercana ala entonación justay a la afinación pitagórica, y es la base dela teoría musical turca.   

• Helmholtz, H. (2005) [1877 (4.ª edición en alemán), 1885 (2.ª edición en inglés)]. Sobre las sensaciones del sonido como base fisiológica de la teoría de la música. Traducido por Ellis, AJ (edición reimpresa). Whitefish, MT: Kellinger Publishing. ISBN 978-1-41917893-1. OCLC  71425252 – vía Internet Archive (archive.org).
  — Una obra fundamental sobre la acústica y la percepción del sonido. Especialmente el material del Apéndice XX: Adiciones del traductor , páginas 430–556 (páginas 451–577 en formato PDF) (véase también el artículo wiki On Sensations of Tone [Sobre las sensaciones del sonido ])

• Introducción a las afinaciones históricas por Kyle Gann
• Wiki de Xenharmonic sobre EDO versus temperamentos iguales
• Centro de Música Microtonal de la Fundación Huygens-Fokker
• A. Orlandini: Acústica musical
• "Temperamento" de Un suplemento a la enciclopedia del señor Chambers (1753)
• Barbieri, Patrizio. Música e instrumentos enarmónicos, 1470-1900. (2008) Latina, Il Levante Librería Editrice
• Música microtonal fractal, Jim Kukula .
• Todas las citas existentes del siglo XVIII sobre JS Bach y el temperamento
• Dominic Eckersley: "Rosetta revisitada: el temperamento muy ordinario de Bach"
• Temperamentos de pozo, basados ​​en la definición de Werckmeister
• CARDINALIDADES FAVORECIDAS DE ESCALAS por P ETER B UCH