Varillas de conteo
| Parte de una serie sobre |
| Sistemas de numeración |
|---|
| List of numeral systems |

| Varillas de conteo | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Nombre chino | |||||||||
| Chino tradicional | 算籌 | ||||||||
| Chino simplificado | 算筹 | ||||||||
| |||||||||
| Nombre chino alternativo | |||||||||
| Chino | 算子 | ||||||||
| |||||||||
| Nombre vietnamita | |||||||||
| Alfabeto vietnamita | que tính / toán trù | ||||||||
| Hán-Nôm | 𣠗併 / 算籌 | ||||||||
| Nombre coreano | |||||||||
| Hangul | 산가지 / 산목 | ||||||||
| Hanja | 算가지 / 算木 | ||||||||
| |||||||||
| Nombre japonés | |||||||||
| Kanji | 算木 / 算籌 | ||||||||
| Hiragana | さんぎ / さんちゅう | ||||||||
| |||||||||
Las barras de conteo (筭) son barras pequeñas, normalmente de 3 a 14 cm (1 a 6 pulgadas) de largo, que usaban los matemáticos para realizar cálculos en el antiguo este de Asia . Se colocaban de forma horizontal o vertical para representar cualquier número entero o racional .
Las formas escritas basadas en ellos se denominan numerales de varilla . Son un verdadero sistema de numeración posicional con dígitos del 1 al 9 y un espacio en blanco para el 0, desde el período de los Estados Combatientes (circa 475 a. C.) [1] hasta el siglo XVI.
Historia
Los aritméticos chinos utilizaban varillas contadoras hace más de dos mil años.
En 1954, se encontraron cuarenta y tantos bastones de conteo del período de los Reinos Combatientes (siglo V a. C. a 221 a. C.) en la tumba Chu n.° 15 de Zuǒjiāgōngshān (左家公山) en Changsha , Hunan . [2] [3] [ verificación fallida ]
En 1973, los arqueólogos desenterraron una serie de escrituras en madera de una tumba en Hubei que datan del período de la dinastía Han (206 a. C. a 220 d. C.). En una de las escrituras de madera estaba escrito: "当利二月定算𝍥". [ cita requerida ] Este es uno de los primeros ejemplos del uso de numerales con varillas para contar en la escritura.
En 1972 se excavó en Mawangdui M3, Changsha, provincia de Hunan, una caja lacada cuadrada que data de alrededor del año 168 a. C. y que contiene un tablero de ajedrez cuadrado con los patrones TLV, piezas de ajedrez, varillas de conteo y otros elementos. [4] [5]
En 1976, se desenterró un paquete de varillas de contar de la era Han occidental (202 a. C. a 9 d. C.) hechas de huesos en el condado de Qianyang en Shaanxi . [6] [7] El uso de varillas de contar debe ser anterior a él; Sunzi ( c. 544 a c. 496 a. C.), un estratega militar al final del período de Primavera y Otoño de 771 a. C. al siglo V a. C., menciona su uso para hacer cálculos para ganar guerras antes de entrar en batalla; [8] Laozi (fallecido en 531 a. C.), escribiendo en el período de los Reinos Combatientes, dijo que "una buena calculadora no usa varillas de contar". [9] El Libro de Han (terminado en 111 d. C.) registró: "calculan con bambú, de un fen de diámetro, seis cun de longitud, dispuestos en un paquete hexagonal de doscientas setenta y una piezas". [10]
Al principio, las varillas de cálculo tenían una sección transversal redonda, pero en la época de la dinastía Sui (581 a 618 d. C.) los matemáticos usaban varillas triangulares para representar números positivos y varillas rectangulares para números negativos . [ cita requerida ]

Después del florecimiento del ábaco [ ¿cuándo? ] , las varillas de conteo se abandonaron, excepto en Japón, donde los numerales de varilla se convirtieron en una notación simbólica para el álgebra .
Usando varillas de conteo




Las barras de conteo representan los dígitos por el número de barras, y la barra perpendicular representa cinco. Para evitar confusiones, se utilizan alternativamente las formas verticales y horizontales. Generalmente, los números de barra verticales se utilizan para la posición de las unidades, centenas, decenas de millar, etc., mientras que los números de barra horizontales se utilizan para las decenas, millar, centenas de millar, etc. Está escrito en Sunzi Suanjing que "uno es vertical, diez es horizontal". [11]
Las barras rojas representan números positivos y las barras negras representan números negativos . [12] Los antiguos chinos entendían claramente los números negativos y el cero (dejando un espacio en blanco para él), aunque no tenían ningún símbolo para este último. Los Nueve Capítulos sobre el Arte Matemático , que se compusieron principalmente en el siglo I d.C., establecían "(al usar la resta) restar números con el mismo signo, sumar números con diferentes signos, restar un número positivo de cero para obtener un número negativo y restar un número negativo de cero para obtener un número positivo". [13] [14] Más tarde, a veces se usaba una piedra de go para representar el cero.
Esta alternancia de la forma vertical y horizontal de los numerales de varilla es muy importante para comprender correctamente la transcripción escrita de los numerales de varilla en los manuscritos. Por ejemplo, en Licheng suanjin, 81 se transcribió como , y 108 se transcribió como ; está claro que este último claramente tenía un cero en blanco en el "tablero de conteo" (es decir, el suelo o la estera), aunque en la transcripción escrita, no había ningún espacio en blanco. En el mismo manuscrito, 405 se transcribió como , con un espacio en blanco en el medio por razones obvias, y de ninguna manera podría interpretarse como "45" . En otras palabras, los numerales de varilla transcritos pueden no ser posicionales, pero en el tablero de conteo, sí lo son. es una imagen exacta del número de varilla de conteo 405 sobre una mesa o el suelo.









Valor posicional
El valor de un número depende de su posición física en el tablero de conteo. Un 9 en la posición más a la derecha del tablero representa 9. Mover el grupo de varillas que representan el 9 una posición a la izquierda (es decir, al lugar de las decenas) da 9[] o 90. Desplazarse nuevamente a la izquierda a la tercera posición (al lugar de las centenas) da 9[][] o 900. Cada vez que uno mueve un número una posición a la izquierda, se multiplica por 10. Cada vez que uno mueve un número una posición a la derecha, se divide por 10. Esto se aplica a números de un solo dígito o números de varios dígitos.
El matemático de la dinastía Song, Jia Xian, utilizó órdenes decimales chinos escritos a mano 步十百千萬 como valor posicional del número de varilla, como se desprende de un facsímil de una página de la Enciclopedia Yongle . Organizó 七萬一千八百二十四 como
- El hombre que se fue
- El hombre que practicaba yoga
Trató los números de orden chinos como marcadores de valor posicional y 七一八二四 se convirtió en un número decimal de valor posicional. Luego escribió los números de varilla de acuerdo con su valor posicional:
| Asi | A mí | Bueno | Asi | Yo |
|---|---|---|---|---|
| 萬 | 千 | 百 | 十 | pero |
 |  |  |  |  |
En Japón, los matemáticos colocaban varillas de conteo sobre un tablero de conteo, una hoja de tela con cuadrículas, y usaban solo formas verticales que se basaban en las cuadrículas. Un libro de matemáticas japonés del siglo XVIII tiene un diagrama de tablero de conteo de damas, con los símbolos de orden de magnitud "千百十一分厘毛" (millar, centena, decena, unidad, décima, centésima, milésima). [15]
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |  |  |  |  |  |  |  |  | |
| Horizontal |  |  |  |  |  |  |  |  |  |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |  |  |  |  |  |  |  |  | |
| Horizontal |  |  |  |  |  |  | 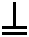 |  | 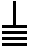 |
Ejemplos:
| 231 |  |  |  | |
|---|---|---|---|---|
| 5089 |  |  |  | |
| −407 |  |  | ||
| −6720 |  |  |  |
Números de varilla
Los numerales de varillas son un sistema de numeración posicional formado por formas de varillas de conteo. Los números positivos se escriben tal como están y los números negativos se escriben con una barra inclinada en el último dígito. La barra vertical en las formas horizontales 6 a 9 se dibuja más corta para tener la misma altura de carácter.
El círculo (〇) se utiliza para representar el 0. Muchos historiadores creen que fue importado de los numerales indios por Gautama Siddha en el año 718, [13] pero algunos creen que fue creado a partir del relleno de espacio de texto chino "□", y otros creen que los indios lo adquirieron de China, porque se asemeja a un símbolo filosófico confuciano para "nada". [16]
En el siglo XIII, los matemáticos de la dinastía Song del Sur cambiaron los dígitos del 4, 5 y 9 para reducir los trazos. [16] Las nuevas formas horizontales acabaron transformándose en numerales de Suzhou . Los japoneses siguieron utilizando las formas tradicionales.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |  |  |  |  |  |  |  |  |  |
| Horizontal |  |  |  |  |  |  |  | 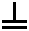 |  |  |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |  |  | 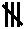 |  | 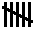 |  |  |  | 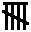 |
| Horizontal |  |  |  |  |  |  |  |  |  |  |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |  |  |  | 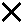 | 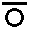 |  |  |  | 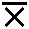 |
| Horizontal |  |  |  |  | 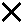 |  |  | 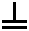 |  |  |
Ejemplos:
| Tradicional | Canción del sur | |
|---|---|---|
| 231 |    |    |
| 5089 |     |    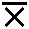 |
| −407 |    | 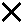   |
| −6720 |     |     |
En Japón, Seki Takakazu desarrolló los numerales de varilla en notación simbólica para el álgebra y mejoró drásticamente las matemáticas japonesas . [13] Después de su período, se desarrolló el sistema de numeración posicional utilizando caracteres numéricos chinos , y los numerales de varilla se usaron solo para los signos más y menos .
| Occidental | Seki | Después de Seki |
|---|---|---|
| x + y + 246 |   甲乙 甲乙   |   El hombre que El hombre que  se convirtió en hombre se convirtió en hombre |
| 5 x − 6 y |   甲乙 甲乙 |  El hombre que El hombre que  se fue se fue |
| 7x |  甲乙 甲乙 |  七甲乙 七甲乙 |
| 8 x / y | N / A | 乙 八甲[ dudoso – discutir ] 八甲[ dudoso – discutir ] |
Fracciones

Una fracción se expresaba con números de barra como dos números de barra uno sobre otro (sin ningún otro símbolo, como la barra horizontal moderna). [ cita requerida ]
Cálculo de varillas
El método para usar varillas de conteo para el cálculo matemático se llamó cálculo de varillas o cálculo de varillas (筹算). El cálculo de varillas se puede utilizar para una amplia gama de cálculos, incluyendo encontrar el valor de π , encontrar raíces cuadradas , raíces cúbicas o raíces de orden superior y resolver un sistema de ecuaciones lineales .
Antes de la introducción del cero escrito, se utilizaba un espacio para indicar que no había unidades y se adoptó la rotación del carácter en la columna de unidades subsiguiente, en 90°, para ayudar a reducir la ambigüedad en los valores de registro calculados en las varillas. [17] Por ejemplo, 107 (𝍠 𝍧) y 17 (𝍩𝍧) se distinguirían por rotación, aunque múltiples unidades de cero podrían generar ambigüedad, por ejemplo, 1007 (𝍩 𝍧) y 10007 (𝍠 𝍧). Una vez que entró en juego el cero escrito, los numerales de varilla se volvieron independientes y su uso de hecho sobrevive a las varillas de conteo, después de su reemplazo por el ábaco . Una variación de los numerales de varilla horizontales, los numerales de Suzhou, todavía se usan para la contabilidad y en la prescripción de medicina herbal en los barrios chinos de algunas partes del mundo.
Unicode
Unicode 5.0 incluye numerales de varilla de conteo en su propio bloque en el Plano Multilingüe Suplementario (SMP) desde U+1D360 hasta U+1D37F. Los puntos de código para los dígitos horizontales 1–9 son U+1D360 a U+1D368 y aquellos para los dígitos verticales 1–9 son U+1D369 a U+1D371. Los primeros se denominan dígitos de unidad y los segundos se denominan dígitos de decenas , [18] [19] lo cual es opuesto a la convención descrita anteriormente. El Estándar Unicode establece que la orientación de los caracteres Unicode sigue la convención de la dinastía Song, que difiere de la práctica de la dinastía Han que representaba los dígitos como líneas verticales y las decenas como líneas horizontales. [20] El cero debe representarse con U+3007 (〇, número ideográfico cero) y el signo negativo debe representarse con U+20E5 (combinando superposición de solidus invertido). [21] Como estos se agregaron recientemente al conjunto de caracteres y están incluidos en el SMP, la compatibilidad de fuentes aún puede ser limitada.
| Numeración de varillas [1] [2] Tabla de códigos del Consorcio Unicode oficial (PDF) | ||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | do | D | mi | F | |
| U+1D36x | 𝍠 | 𝍡 | 𝍢 | 𝍣 | 𝍤 | 𝍥 | 𝍦 | 𝍧 | 𝍨 | 𝍩 | 𝍪 | 𝍫 | 𝍬 | 𝍭 | 𝍮 | 𝍯 |
| U+1D37x | 𝍰 | 𝍱 | 𝍲 | 𝍳 | 𝍴 | 𝍵 | 𝍶 | 𝍷 | 𝍸 | |||||||
Notas
| ||||||||||||||||
Véase también
Referencias
- ^ Lay-Yong, Lam (1986). "Los orígenes conceptuales de nuestro sistema numérico y la forma simbólica del álgebra". Archivo de Historia de las Ciencias Exactas . 36 (3): 183–195. ISSN 0003-9519.
- ^ 中国独特的计算工具, archivado desde el original el 21 de noviembre de 2007 , consultado el 16 de diciembre de 2007Año 1954战国时期楚墓。墓中出土了一个竹筒,里面盛放着戥秤、砝码、毛笔以及四十余根长度约为十二厘米的竹片。这是最早发现也是最古的算筹实物。En inglés: en 1954, los arqueólogos descubrieron una tumba de la dinastía Chu del Período de los Reinos Combatientes, que tiene más de 2.100 años de antigüedad, en la montaña Zuojiagong en Changsha, provincia de Hunan, en el curso medio del río Yangtze. En la tumba se descubrió un tubo de bambú que contenía una balanza, pesas, un cepillo y más de 40 piezas de bambú de unos 12 centímetros de largo. Se trata del ábaco más antiguo y antiguo descubierto hasta la fecha.
- ^ Matemáticas de la antigua China Archivado el 26 de enero de 2011 en Wayback Machine. – Copyright © 2010 – TutorVista.com, Todos los derechos reservados.
- ^ WONG, Pui Yin Marianne (marzo de 2006). "Los Siling (cuatro animales cardinales) en el arte pictórico Han - vol. 1" (PDF) . SOAS : 370, 416.
- ^ "Blog de BabelStone: El juego perdido de Liubo, parte 4: tableros de juego y equipamiento". www.babelstone.co.uk . Consultado el 5 de agosto de 2020 .
- ^ Wu Wenjun ed, Gran serie de historia de las matemáticas chinas, vol. 1, pág. 371
- ^ Lam, Lay Yong; Ang, Tian Se (2004). Huellas fugaces: Rastreando la concepción de la aritmética y el álgebra en la antigua China. World Scientific. ISBN 978-981-256-725-3.
- ^ 孫子: 夫未戰而廟算勝者,得算多也
- ^ 老子: 善數者不用籌策.
- ^ Zhu, Yiwen (2018). "¿Cómo se introdujeron los cálculos escritos occidentales en China? — Un análisis del Tongwen suanzhi (Guía aritmética en el lenguaje común, 1613)". ResearchGate . Consultado el 5 de agosto de 2020 .
- ^ Wikisource chino 孫子算經: 先識其位,一從十橫,百立千僵,千十相望,萬百相當.
- ^ Wikisource chino, 夢溪筆談: 如算法用赤籌、黑籌,以別正負之數。
- ^ abc Wáng, Qīngxiáng (1999), Sangi o koeta otoko (El hombre que excedió las varillas de contar) , Tokio: Tōyō Shoten, ISBN 4-88595-226-3
- ^ Wikisource chino 正負術曰: 同名相除,異名相益,正無入負之,負無入正之。其異名相除,同名相益,正無入正之,負無入負之。
- ^ Karl Menninger , Palabras numéricas y símbolos numéricos, pág. 369, MIT Press, 1970
- ^ ab Qian, Baocong (1964), Zhongguo Shuxue Shi (La historia de las matemáticas chinas) , Beijing: Kexue Chubanshe
- ^ "Números chinos". Historia de las matemáticas . Consultado el 28 de abril de 2024 .
- ^ Christopher Cullen y John H. Jenkins, Propuesta para añadir numerales de varillas de conteo chinos a Unicode e ISO/IEC 10646, 2004
- ^ El estándar Unicode, versión 5.0 – Edición electrónica (PDF) , Unicode, Inc., 2006, pág. 558
- ^ El estándar Unicode, versión 15.0 – Edición electrónica (PDF) , Unicode, Inc., 2022, págs. 869–870
- ^ El estándar Unicode, versión 5.0 – Edición electrónica (PDF) , Unicode, Inc., 2006, págs. 499–500
Enlaces externos
Para ver las antiguas varillas de conteo y obtener más explicaciones, puede visitar los sitios
- https://web.archive.org/web/20010217175749/http://www.math.sfu.ca/histmath/China/Beginning/Rod.html
- http://mathforum.org/library/drmath/view/52557.html
- Varillas de conteo en China (en chino) ( Traducir al español: Google, Bing, Yandex)
- Varas de conteo y piedras de Go de un matemático japonés alrededor de 1872 (en japonés) ( Traducir al español: Google, Bing, Yandex)