Signo (matemáticas)
Este artículo necesita citas adicionales para su verificación . ( August 2020 ) |

En matemáticas , el signo de un número real es su propiedad de ser positivo, negativo o 0. Según las convenciones locales, se puede considerar que el cero tiene su propio signo único, no tiene signo o tiene signo positivo y negativo. En algunos contextos, tiene sentido distinguir entre un cero positivo y uno negativo .
En matemáticas y física, la frase "cambio de signo" se asocia con el intercambio de un objeto por su inverso aditivo (multiplicación por −1 , negación), una operación que no se limita a los números reales. Se aplica, entre otros objetos, a vectores, matrices y números complejos, que no están prescritos para ser solo positivos, negativos o cero.
La palabra "signo" también se utiliza a menudo para indicar aspectos binarios de objetos matemáticos o científicos, como pares e impares ( signo de una permutación ), sentido de orientación o rotación ( cw/ccw ), límites unilaterales y otros conceptos descritos en el § Otros significados más abajo.
Signo de un numero
Los números de varios sistemas numéricos, como los enteros , racionales , complejos , cuaterniones , octoniones , etc., pueden tener múltiples atributos que fijan ciertas propiedades de un número. Un sistema numérico que tiene la estructura de un anillo ordenado contiene un número único que, cuando se suma con cualquier número, deja este último inalterado. Este número único se conoce como elemento de identidad aditivo del sistema . Por ejemplo, los números enteros tienen la estructura de un anillo ordenado. Este número se denota generalmente como 0. Debido al orden total en este anillo, hay números mayores que cero, llamados números positivos . Otra propiedad requerida para que un anillo esté ordenado es que, para cada número positivo, existe un número correspondiente único menor que 0 cuya suma con el número positivo original es 0. Estos números menores que 0 se llaman números negativos . Los números en cada uno de estos pares son sus respectivos inversos aditivos . Este atributo de un número, que es exclusivamente cero (0) , positivo (+) o negativo (−) , se llama su signo y a menudo se codifica con los números reales 0 , 1 y −1 , respectivamente (de manera similar a la forma en que se define la función signo ). [1] Dado que los números racionales y reales también son anillos ordenados (de hecho, campos ordenados ), el atributo signo también se aplica a estos sistemas numéricos.
Cuando se utiliza un signo menos entre dos números, representa la operación binaria de resta. Cuando se escribe un signo menos antes de un solo número, representa la operación unaria de producir el inverso aditivo (a veces llamado negación ) del operando. De manera abstracta, entonces, la diferencia de dos números es la suma del minuendo con el inverso aditivo del sustraendo. Mientras que 0 es su propio inverso aditivo ( −0 = 0 ), el inverso aditivo de un número positivo es negativo y el inverso aditivo de un número negativo es positivo. Una doble aplicación de esta operación se escribe como −(−3) = 3 . El signo más se usa predominantemente en álgebra para denotar la operación binaria de adición, y solo raramente para enfatizar la positividad de una expresión.
En la notación numérica común (usada en aritmética y en otros ámbitos), el signo de un número suele hacerse explícito colocando un signo más o un signo menos antes del número. Por ejemplo, +3 denota "tres positivo" y −3 denota "tres negativo" (algebraicamente: el inverso aditivo de 3 ). Sin un contexto específico (o cuando no se proporciona un signo explícito), un número se interpreta por defecto como positivo. Esta notación establece una fuerte asociación del signo menos " − " con los números negativos y del signo más "+" con los números positivos.
Signo de cero
Dentro de la convención de que cero no es ni positivo ni negativo, se puede asignar un valor de signo específico 0 al valor numérico 0 . Esto se explota en la función - , tal como se define para los números reales. [1] En aritmética, +0 y −0 denotan ambos el mismo número 0 . Generalmente no hay peligro de confundir el valor con su signo, aunque la convención de asignar ambos signos a 0 no permite inmediatamente esta discriminación.
En algunos países europeos, por ejemplo en Bélgica y Francia, el 0 se considera tanto positivo como negativo siguiendo la convención establecida por Nicolas Bourbaki . [2]
En algunos contextos, como las representaciones de punto flotante de números reales dentro de las computadoras, es útil considerar versiones con signo de cero, donde los ceros con signo hacen referencia a representaciones de números diferentes y discretas (ver representaciones de números con signo para más información).
Los símbolos +0 y −0 rara vez aparecen como sustitutos de 0+ y 0− , utilizados en cálculo y análisis matemático para límites unilaterales ( límite lateral derecho y límite lateral izquierdo, respectivamente). Esta notación se refiere al comportamiento de una función cuando su variable de entrada real se acerca a 0 a lo largo de valores positivos (o negativos); los dos límites no necesitan existir o coincidir.
Terminología de los signos
Cuando se dice que 0 no es ni positivo ni negativo, las siguientes frases pueden referirse al signo de un número:
- Un número es positivo si es mayor que cero.
- Un número es negativo si es menor que cero.
- Un número no es negativo si es mayor o igual a cero.
- Un número no es positivo si es menor o igual a cero.
Cuando se dice que 0 es tanto positivo como negativo, [ cita requerida ] se utilizan frases modificadas para referirse al signo de un número:
- Un número es estrictamente positivo si es mayor que cero.
- Un número es estrictamente negativo si es menor que cero.
- Un número es positivo si es mayor o igual a cero.
- Un número es negativo si es menor o igual a cero.
Por ejemplo, el valor absoluto de un número real es siempre "no negativo", pero no necesariamente "positivo" en la primera interpretación, mientras que en la segunda interpretación se le llama "positivo", aunque no necesariamente "estrictamente positivo".
La misma terminología se utiliza a veces para funciones que dan valores reales u otros valores con signo. Por ejemplo, una función se llamaría función positiva si sus valores son positivos para todos los argumentos de su dominio, o función no negativa si todos sus valores son no negativos.
Números complejos
Los números complejos son imposibles de ordenar, por lo que no pueden llevar la estructura de un anillo ordenado y, en consecuencia, no se pueden dividir en números complejos positivos y negativos. Sin embargo, comparten un atributo con los reales, que se llama valor absoluto o magnitud . Las magnitudes son siempre números reales no negativos, y a todo número distinto de cero le corresponde un número real positivo, su valor absoluto .
Por ejemplo, el valor absoluto de −3 y el valor absoluto de 3 son ambos iguales a 3. Esto se escribe en símbolos como | −3 | = 3 y | 3 | = 3 .
En general, cualquier valor real arbitrario se puede especificar por su magnitud y su signo. Si se utiliza la codificación estándar, cualquier valor real se obtiene mediante el producto de la magnitud y el signo en la codificación estándar. Esta relación se puede generalizar para definir un signo para números complejos.
Puesto que los números reales y complejos forman un cuerpo y contienen a los reales positivos, también contienen los recíprocos de las magnitudes de todos los números distintos de cero. Esto significa que cualquier número distinto de cero puede multiplicarse por el recíproco de su magnitud, es decir, dividirse por su magnitud. Es inmediato que el cociente de cualquier número real distinto de cero por su magnitud da exactamente su signo. Por analogía, el signo de un número complejo z puede definirse como el cociente de z y su magnitud | z | . El signo de un número complejo es el exponencial del producto de su argumento por la unidad imaginaria. representa en cierto sentido su argumento complejo. Esto debe compararse con el signo de los números reales, excepto con Para la definición de una función signo compleja, véase § Función signo compleja a continuación.
Funciones de los signos
Cuando se trabaja con números, suele ser conveniente tener su signo disponible como número. Esto se logra mediante funciones que extraen el signo de cualquier número y lo asignan a un valor predefinido antes de ponerlo a disposición para cálculos posteriores. Por ejemplo, podría ser ventajoso formular un algoritmo complejo solo para valores positivos y ocuparse del signo solo después.
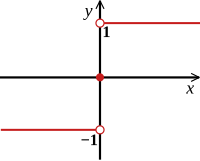
Función de signo real
La función signo o función signum extrae el signo de un número real, mapeando el conjunto de números reales al conjunto de los tres reales. Puede definirse de la siguiente manera: [1] Por lo tanto, sgn( x ) es 1 cuando x es positivo, y sgn( x ) es −1 cuando x es negativo. Para valores distintos de cero de x , esta función también puede definirse mediante la fórmula donde | x | es el valor absoluto de x .
Función de signo compleja
Mientras que un número real tiene una dirección unidimensional, un número complejo tiene una dirección bidimensional. La función de signo compleja requiere la magnitud de su argumento z = x + iy , que se puede calcular como
De manera análoga a lo anterior, la función de signo complejo extrae el signo complejo de un número complejo asignando el conjunto de números complejos distintos de cero al conjunto de números complejos unimodulares, y 0 a 0 : puede definirse de la siguiente manera:
Sea z también expresado por su magnitud y uno de sus argumentos φ como z = | z |⋅ e iφ , entonces [3]
Esta definición también puede reconocerse como un vector normalizado, es decir, un vector cuya dirección no cambia y cuya longitud está fijada en la unidad . Si el valor original era R,θ en forma polar, entonces sign(R, θ) es 1 θ. La extensión de sign() o signum() a cualquier número de dimensiones es obvia, pero esto ya se ha definido como normalizar un vector.
Señales por convención
En situaciones en las que existen exactamente dos posibilidades en igualdad de condiciones para un atributo, estas suelen etiquetarse por convención como más y menos , respectivamente. En algunos contextos, la elección de esta asignación (es decir, qué rango de valores se considera positivo y cuál negativo) es natural, mientras que en otros contextos, la elección es arbitraria, lo que hace necesaria una convención de signos explícita, siendo el único requisito el uso consistente de la convención.
Señal de un ángulo

En muchos contextos, es común asociar un signo con la medida de un ángulo , en particular un ángulo orientado o un ángulo de rotación . En tal situación, el signo indica si el ángulo está en sentido horario o antihorario. Aunque se pueden utilizar diferentes convenciones, es común en matemáticas que los ángulos en sentido antihorario cuenten como positivos y los ángulos en el sentido horario cuenten como negativos. [4]
También es posible asociar un signo a un ángulo de rotación en tres dimensiones, suponiendo que el eje de rotación se ha orientado. En concreto, una rotación hacia la derecha alrededor de un eje orientado suele considerarse positiva, mientras que una rotación hacia la izquierda se considera negativa.
Un ángulo que es el negativo de un ángulo dado tiene un arco igual, pero el eje opuesto . [5]
Señal de un cambio
Cuando una cantidad x cambia con el tiempo, el cambio en el valor de x se define normalmente mediante la ecuación
Usando esta convención, un aumento en x cuenta como un cambio positivo, mientras que una disminución de x cuenta como un cambio negativo. En cálculo , esta misma convención se usa en la definición de la derivada . Como resultado, cualquier función creciente tiene derivada positiva, mientras que cualquier función decreciente tiene derivada negativa.
Señal de una dirección
Al estudiar los desplazamientos y movimientos unidimensionales en geometría analítica y física , es común etiquetar las dos direcciones posibles como positivas y negativas. Debido a que la línea numérica generalmente se dibuja con números positivos a la derecha y números negativos a la izquierda, una convención común es que los movimientos hacia la derecha tengan un signo positivo y los movimientos hacia la izquierda, un signo negativo.
En el plano cartesiano , las direcciones hacia la derecha y hacia arriba se consideran generalmente positivas, siendo la derecha la dirección x positiva y hacia arriba la dirección y positiva. Si un vector de desplazamiento se separa en sus componentes vectoriales , entonces la parte horizontal será positiva para el movimiento hacia la derecha y negativa para el movimiento hacia la izquierda, mientras que la parte vertical será positiva para el movimiento hacia arriba y negativa para el movimiento hacia abajo.
De la misma manera, una velocidad negativa (tasa de cambio de desplazamiento) implica una velocidad en dirección opuesta , es decir, retroceder en lugar de avanzar; un caso especial es la velocidad radial .
En el espacio 3D , las nociones relacionadas con el signo se pueden encontrar en las dos orientaciones normales y la orientabilidad en general.
La signatura en la informática
| bit más significativo | |||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | 127 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | 126 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | = | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | -1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | -2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | −127 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | −128 |
| La mayoría de las computadoras utilizan el complemento a dos para representar el signo de un número entero. | |||||||||
En informática , un valor entero puede tener signo o no, dependiendo de si la computadora lleva un registro del signo del número. Al restringir una variable entera a valores no negativos únicamente, se puede utilizar un bit más para almacenar el valor de un número. Debido a la forma en que se realiza la aritmética de números enteros dentro de las computadoras, las representaciones de números con signo generalmente no almacenan el signo como un solo bit independiente, sino que utilizan, por ejemplo, el complemento a dos .
Por el contrario, los números reales se almacenan y se manipulan como valores de punto flotante . Los valores de punto flotante se representan utilizando tres valores separados: mantisa, exponente y signo. Dado este bit de signo separado, es posible representar tanto el cero positivo como el negativo. La mayoría de los lenguajes de programación normalmente tratan el cero positivo y el cero negativo como valores equivalentes, aunque proporcionan medios por los cuales se puede detectar la distinción.
Otros significados
Además del signo de un número real, la palabra signo también se utiliza de diversas formas relacionadas en las matemáticas y otras ciencias:
- Las palabras hasta el signo significan que, para una cantidad q , se sabe que q = Q o q = − Q para cierto Q . A menudo se expresa como q = ± Q . Para números reales, significa que solo se conoce el valor absoluto | q | de la cantidad. Para números complejos y vectores , una cantidad conocida hasta el signo es una condición más fuerte que una cantidad con magnitud conocida : además de Q y − Q , hay muchos otros valores posibles de q tales que | q | = | Q | .
- El signo de una permutación se define como positivo si la permutación es par y negativo si la permutación es impar.
- En teoría de grafos , un grafo con signo es un grafo en el que cada arista ha sido marcada con un signo positivo o negativo.
- En análisis matemático , una medida con signo es una generalización del concepto de medida en la que la medida de un conjunto puede tener valores positivos o negativos.
- El concepto de distancia señalizada se utiliza para transmitir lado , interior o exterior.
- Las ideas de área con signo y volumen con signo se utilizan a veces cuando resulta conveniente que determinadas áreas o volúmenes se consideren negativos. Esto es particularmente cierto en la teoría de determinantes . En un espacio vectorial orientado (abstracto) , cada base ordenada del espacio vectorial se puede clasificar como orientada positiva o negativamente.
- En una representación de dígitos con signo , cada dígito de un número puede tener un signo positivo o negativo.
- En física , cualquier carga eléctrica tiene un signo, ya sea positivo o negativo. Por convención, una carga positiva es una carga con el mismo signo que la de un protón , y una carga negativa es una carga con el mismo signo que la de un electrón .
Véase también
Referencias
- ^ abc Weisstein, Eric W. "Signo". mathworld.wolfram.com . Consultado el 26 de agosto de 2020 .
- ^ Bourbaki, Nicolás. Elementos matemáticos : Algèbre . pag. AVI.4..
- ^ "Función Signum". www.cs.cas.cz . Consultado el 26 de agosto de 2020 .
- ^ "Signo de ángulos | ¿Qué es un ángulo? | Ángulo positivo | Ángulo negativo". Matemáticas Solo matemáticas . Consultado el 26 de agosto de 2020 .
- ^ Alexander Macfarlane (1894) "Teoremas fundamentales del análisis generalizados para el espacio", página 3, enlace vía Internet Archive










