Serie de Taylor

Part of a series of articles about
Calculus
${\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)}$
Fundamental theorem Limits Continuity Rolle's theorem Mean value theorem Inverse function theorem
Differential Definitions Derivative (generalizations) Differential infinitesimal of a function total Concepts Differentiation notation Second derivative Implicit differentiation Logarithmic differentiation Related rates Taylor's theorem Rules and identities Sum Product Chain Power Quotient L'Hôpital's rule Inverse General Leibniz Faà di Bruno's formula Reynolds
Integral Lists of integrals Integral transform Leibniz integral rule Definitions Antiderivative Integral (improper) Riemann integral Lebesgue integration Contour integration Integral of inverse functions Integration by Parts Discs Cylindrical shells Substitution (trigonometric, tangent half-angle, Euler) Euler's formula Partial fractions (Heaviside's method) Changing order Reduction formulae Differentiating under the integral sign Risch algorithm
Series Geometric (arithmetico-geometric) Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector Gradient Divergence Curl Laplacian Directional derivative Identities Theorems Gradient Green's Stokes' Divergence generalized Stokes Helmholtz decomposition
Multivariable Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian Hessian
Advanced Calculus on Euclidean space Generalized functions Limit of distributions
Specialized Fractional Malliavin Stochastic Variations
Miscellanea Precalculus History Glossary List of topics Integration Bee Mathematical analysis Nonstandard analysis
v t e

En matemáticas , la serie de Taylor o desarrollo de Taylor de una función es una suma infinita de términos que se expresan en términos de las derivadas de la función en un único punto. Para la mayoría de las funciones comunes, la función y la suma de su serie de Taylor son iguales cerca de este punto. Las series de Taylor reciben su nombre de Brook Taylor , quien las introdujo en 1715. Una serie de Taylor también se denomina serie de Maclaurin cuando 0 es el punto donde se consideran las derivadas, en honor a Colin Maclaurin , quien hizo un uso extensivo de este caso especial de la serie de Taylor en el siglo XVIII.

La suma parcial formada por los primeros n + 1 términos de una serie de Taylor es un polinomio de grado n que se llama el n º polinomio de Taylor de la función. Los polinomios de Taylor son aproximaciones de una función, que se vuelven generalmente más precisas a medida que n aumenta. El teorema de Taylor proporciona estimaciones cuantitativas sobre el error introducido por el uso de tales aproximaciones. Si la serie de Taylor de una función es convergente , su suma es el límite de la secuencia infinita de los polinomios de Taylor. Una función puede diferir de la suma de su serie de Taylor, incluso si su serie de Taylor es convergente. Una función es analítica en un punto x si es igual a la suma de su serie de Taylor en algún intervalo abierto (o disco abierto en el plano complejo ) que contiene x . Esto implica que la función es analítica en cada punto del intervalo (o disco).

La serie de Taylor de una función real o compleja f  ( x ) , que es infinitamente diferenciable en un número real o complejo a , es la serie de potencias Aquí, n ! denota el factorial de n . La función f ^{( n )} ( a ) denota la derivada n ésima de f evaluada en el punto a . La derivada de orden cero de f se define como f misma y ( x − a ) ⁰ y 0! se definen como 1 . Esta serie se puede escribir utilizando la notación sigma , como en la fórmula del lado derecho. ^[1] Con a = 0 , la serie de Maclaurin toma la forma: ^[2] $${\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots =\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}.}$$ $${\displaystyle f(0)+{\frac {f'(0)}{1!}}x+{\frac {f''(0)}{2!}}x^{2}+{\frac {f'''(0)}{3!}}x^{3}+\cdots =\sum _{n=0}^{\infty }{\frac {f^{(n)}(0)}{n!}}x^{n}.}$$

La serie de Taylor de cualquier polinomio es el polinomio mismo.

La serie Maclaurin de ⁠1/1 − x⁠ es la serie geométrica

$${\displaystyle 1+x+x^{2}+x^{3}+\cdots .}$$

Entonces, sustituyendo x por 1 − x , la serie de Taylor de ⁠1/incógnita⁠ en a = 1 es

$${\displaystyle 1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .}$$

Al integrar la serie de Maclaurin anterior, encontramos la serie de Maclaurin de ln(1 − x ) , donde ln denota el logaritmo natural :

$${\displaystyle -x-{\tfrac {1}{2}}x^{2}-{\tfrac {1}{3}}x^{3}-{\tfrac {1}{4}}x^{4}-\cdots .}$$

La serie de Taylor correspondiente de ln x en a = 1 es

$${\displaystyle (x-1)-{\tfrac {1}{2}}(x-1)^{2}+{\tfrac {1}{3}}(x-1)^{3}-{\tfrac {1}{4}}(x-1)^{4}+\cdots ,}$$

y de manera más general, la serie de Taylor correspondiente de ln x en un punto arbitrario distinto de cero a es:

$${\displaystyle \ln a+{\frac {1}{a}}(x-a)-{\frac {1}{a^{2}}}{\frac {\left(x-a\right)^{2}}{2}}+\cdots .}$$

La serie de Maclaurin de la función exponencial e ^x es

$${\displaystyle {\begin{aligned}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}&={\frac {x^{0}}{0!}}+{\frac {x^{1}}{1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {x^{5}}{5!}}+\cdots \\&=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+{\frac {x^{5}}{120}}+\cdots .\end{aligned}}}$$

La expansión anterior se cumple porque la derivada de e ^x con respecto a x también es e ^x , y e ⁰ es igual a 1. Esto deja los términos ( x − 0) ⁿ en el numerador y n ! en el denominador de cada término en la suma infinita.

El antiguo filósofo griego Zenón de Elea consideró el problema de sumar una serie infinita para lograr un resultado finito, pero lo rechazó como una imposibilidad; ^[3] el resultado fue la paradoja de Zenón . Más tarde, Aristóteles propuso una resolución filosófica de la paradoja, pero el contenido matemático aparentemente quedó sin resolver hasta que lo retomó Arquímedes , como lo había sido antes de Aristóteles por el atomista presocrático Demócrito . Fue a través del método de agotamiento de Arquímedes que se pudo realizar un número infinito de subdivisiones progresivas para lograr un resultado finito. ^[4] Liu Hui empleó de forma independiente un método similar unos siglos después. ^[5]

En el siglo XIV, los primeros ejemplos de series de Taylor específicas (pero no del método general) fueron proporcionados por el matemático indio Madhava de Sangamagrama . ^[6] Aunque no sobrevive ningún registro de su trabajo, los escritos de sus seguidores en la escuela de astronomía y matemáticas de Kerala sugieren que encontró la serie de Taylor para las funciones trigonométricas de seno , coseno y arcotangente (véase serie de Madhava ). Durante los dos siglos siguientes, sus seguidores desarrollaron más expansiones de series y aproximaciones racionales.

A finales de 1670, James Gregory recibió en una carta de John Collins varias series de Maclaurin (${\textstyle \sin x,}$ y ) derivadas por Isaac Newton , y le dijo que Newton había desarrollado un método general para expandir funciones en serie. De hecho, Newton había utilizado un método engorroso que implicaba una larga división de series y una integración término por término, pero Gregory no lo sabía y se propuso descubrir un método general por sí mismo. A principios de 1671, Gregory descubrió algo parecido a la serie general de Maclaurin y envió una carta a Collins que incluía series para (la integral de ), (la integral de sec , la función inversa de Gudermann ), y (la función de Gudermann ). Sin embargo, pensando que simplemente había vuelto a desarrollar un método de Newton, Gregory nunca describió cómo obtuvo estas series, y solo se puede inferir que entendió el método general examinando un trabajo preliminar que había garabateado en el reverso de otra carta de 1671. ^[7]${\textstyle \cos x,}$ ${\textstyle \arcsin x,}$${\textstyle x\cot x}$${\textstyle \arctan x,}$ ${\textstyle \tan x,}$ ${\textstyle \sec x,}$ ${\textstyle \ln \,\sec x}$${\displaystyle \tan }$ ${\textstyle \ln \,\tan {\tfrac {1}{2}}{{\bigl (}{\tfrac {1}{2}}\pi +x{\bigr )}}}$${\textstyle \operatorname {arcsec} {\bigl (}{\sqrt {2}}e^{x}{\bigr )},}$${\textstyle 2\arctan e^{x}-{\tfrac {1}{2}}\pi }$

Entre 1691 y 1692, Isaac Newton escribió una exposición explícita de la serie de Taylor y Maclaurin en una versión inédita de su obra De Quadratura Curvarum . Sin embargo, esta obra nunca se completó y las secciones pertinentes se omitieron de las partes publicadas en 1704 bajo el título Tractatus de Quadratura Curvarum .

No fue hasta 1715 que Brook Taylor publicó finalmente un método general para construir estas series para todas las funciones para las que existen ^[8] , de quien ahora reciben el nombre las series.

La serie de Maclaurin debe su nombre a Colin Maclaurin , un matemático escocés que publicó el caso especial del resultado de Taylor a mediados del siglo XVIII.

Si f  ( x ) está dada por una serie de potencias convergentes en un disco abierto centrado en b en el plano complejo (o un intervalo en la recta real), se dice que es analítica en esta región. Por lo tanto, para x en esta región, f está dada por una serie de potencias convergentes

$${\displaystyle f(x)=\sum _{n=0}^{\infty }a_{n}(x-b)^{n}.}$$

Diferenciando por x la fórmula anterior n veces, y luego estableciendo x = b, obtenemos:

$${\displaystyle {\frac {f^{(n)}(b)}{n!}}=a_{n}}$$

y por lo tanto la expansión en serie de potencias concuerda con la serie de Taylor. Por lo tanto, una función es analítica en un disco abierto centrado en b si y solo si su serie de Taylor converge al valor de la función en cada punto del disco.

Si f  ( x ) es igual a la suma de su serie de Taylor para todo x en el plano complejo, se llama función entera . Los polinomios, la función exponencial e ^x y las funciones trigonométricas seno y coseno son ejemplos de funciones enteras. Ejemplos de funciones que no son enteras incluyen la raíz cuadrada , el logaritmo , la función trigonométrica tangente y su inversa, arctan . Para estas funciones, la serie de Taylor no converge si x está lejos de b . Es decir, la serie de Taylor diverge en x si la distancia entre x y b es mayor que el radio de convergencia . La serie de Taylor se puede utilizar para calcular el valor de una función entera en cada punto, si el valor de la función y de todas sus derivadas se conocen en un solo punto.

Los usos de la serie de Taylor para funciones analíticas incluyen:

1. Las sumas parciales ( polinomios de Taylor ) de la serie se pueden utilizar como aproximaciones de la función. Estas aproximaciones son adecuadas si se incluyen suficientes términos.
2. La diferenciación e integración de series de potencias se puede realizar término por término y, por lo tanto, es particularmente fácil.
3. Una función analítica se extiende de forma única a una función holomorfa en un disco abierto en el plano complejo . Esto hace que la maquinaria del análisis complejo esté disponible.
4. La serie (truncada) se puede utilizar para calcular valores de funciones numéricamente (a menudo reformulando el polinomio en la forma de Chebyshev y evaluándolo con el algoritmo de Clenshaw ).
5. Las operaciones algebraicas se pueden realizar fácilmente en la representación de series de potencias; por ejemplo, la fórmula de Euler se deduce de las expansiones de series de Taylor para funciones trigonométricas y exponenciales. Este resultado es de importancia fundamental en campos como el análisis armónico .
6. Las aproximaciones que utilizan los primeros términos de una serie de Taylor pueden hacer posibles problemas que de otro modo serían irresolubles para un dominio restringido; este enfoque se utiliza a menudo en física.

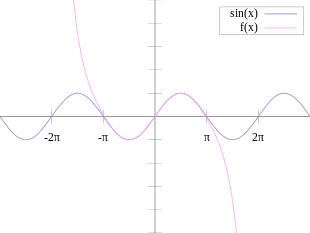
En la imagen se muestra una aproximación precisa del seno x alrededor del punto x = 0. La curva rosa es un polinomio de grado siete:

$${\displaystyle \sin {x}\approx x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}.\!}$$

El error en esta aproximación no es mayor que | x | ⁹  / 9! . Para un ciclo completo centrado en el origen ( −π < x < π ) el error es menor que 0,08215. En particular, para −1 < x < 1 , el error es menor que 0,000003.

En contraste, también se muestra una imagen de la función logaritmo natural ln(1 + x ) y algunos de sus polinomios de Taylor alrededor de a = 0 . Estas aproximaciones convergen a la función solo en la región −1 < x ≤ 1 ; fuera de esta región, los polinomios de Taylor de grado superior son peores aproximaciones para la función.

El error en que se incurre al aproximar una función por su polinomio de Taylor de grado n se denomina residuo y se denota por la función R _n ( x ) . El teorema de Taylor se puede utilizar para obtener un límite para el tamaño del residuo .

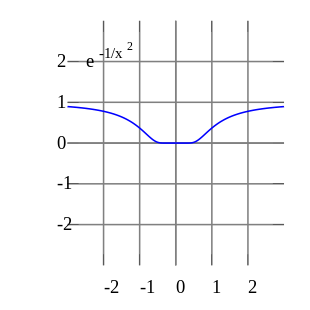
En general, las series de Taylor no necesitan ser convergentes en absoluto. De hecho, el conjunto de funciones con una serie de Taylor convergente es un conjunto exiguo en el espacio de Fréchet de funciones suaves . Incluso si la serie de Taylor de una función f converge, su límite no necesita ser igual al valor de la función f  ( x ) . Por ejemplo, la función

$${\displaystyle f(x)={\begin{cases}e^{-1/x^{2}}&{\text{if }}x\neq 0\\[3mu]0&{\text{if }}x=0\end{cases}}}$$

es infinitamente diferenciable en x = 0 y tiene todas las derivadas cero en ese punto. En consecuencia, la serie de Taylor de f  ( x ) en torno a x = 0 es idénticamente cero. Sin embargo, f  ( x ) no es la función cero, por lo que no es igual a su serie de Taylor en torno al origen. Por lo tanto, f  ( x ) es un ejemplo de una función suave no analítica .

En el análisis real , este ejemplo muestra que existen funciones infinitamente diferenciables f  ( x ) cuyas series de Taylor no son iguales a f  ( x ) incluso si convergen. Por el contrario, las funciones holomorfas estudiadas en el análisis complejo siempre poseen una serie de Taylor convergente, e incluso la serie de Taylor de las funciones meromórficas , que podrían tener singularidades, nunca converge a un valor diferente de la función misma. La función compleja e ^{−1/ z 2} , sin embargo, no tiende a 0 cuando z tiende a 0 a lo largo del eje imaginario, por lo que no es continua en el plano complejo y su serie de Taylor no está definida en 0.

En términos más generales, toda sucesión de números reales o complejos puede aparecer como coeficientes en la serie de Taylor de una función infinitamente diferenciable definida sobre la recta real, una consecuencia del lema de Borel . Como resultado, el radio de convergencia de una serie de Taylor puede ser cero. Incluso existen funciones infinitamente diferenciables definidas sobre la recta real cuya serie de Taylor tiene un radio de convergencia 0 en todas partes. ^[9]

Una función no puede escribirse como una serie de Taylor centrada en una singularidad ; en estos casos, a menudo se puede lograr una expansión en serie si se permiten también potencias negativas de la variable x ; véase la serie de Laurent . Por ejemplo, f  ( x ) = e ^{−1/ x 2} puede escribirse como una serie de Laurent.

La generalización de la serie de Taylor converge al valor de la función misma para cualquier función continua acotada en (0,∞) , y esto se puede hacer utilizando el cálculo de diferencias finitas . Específicamente, el siguiente teorema, debido a Einar Hille , que para cualquier t > 0 , ^[10]

$${\displaystyle \lim _{h\to 0^{+}}\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}{\frac {\Delta _{h}^{n}f(a)}{h^{n}}}=f(a+t).}$$

Aquí Δ^en
_​es el n -ésimo operador de diferencia finita con tamaño de paso h . La serie es precisamente la serie de Taylor, excepto que las diferencias divididas aparecen en lugar de la diferenciación: la serie es formalmente similar a la serie de Newton . Cuando la función f es analítica en a , los términos de la serie convergen a los términos de la serie de Taylor y, en este sentido, generaliza la serie de Taylor habitual.

En general, para cualquier secuencia infinita a _i , se cumple la siguiente identidad de serie de potencias:

$${\displaystyle \sum _{n=0}^{\infty }{\frac {u^{n}}{n!}}\Delta ^{n}a_{i}=e^{-u}\sum _{j=0}^{\infty }{\frac {u^{j}}{j!}}a_{i+j}.}$$

Así, en particular,

$${\displaystyle f(a+t)=\lim _{h\to 0^{+}}e^{-t/h}\sum _{j=0}^{\infty }f(a+jh){\frac {(t/h)^{j}}{j!}}.}$$

La serie de la derecha es el valor esperado de f  ( a + X ) , donde X es una variable aleatoria distribuida por Poisson que toma el valor jh con probabilidad e ^{− t / h} · ⁠( toneladas por hora ) ^j/yo !⁠ . Por lo tanto,

$${\displaystyle f(a+t)=\lim _{h\to 0^{+}}\int _{-\infty }^{\infty }f(a+x)dP_{t/h,h}(x).}$$

La ley de los grandes números implica que la identidad se cumple. ^[11]

A continuación se presentan varias expansiones importantes de la serie de Maclaurin. Todas estas expansiones son válidas para argumentos complejos x .

La función exponencial (con base e ) tiene serie de Maclaurin ^[12]${\displaystyle e^{x}}$

$${\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots .}$$Converge para todo x .

La función generadora exponencial de los números de Bell es la función exponencial del predecesor de la función exponencial:

$${\displaystyle \exp(\exp {x}-1)=\sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}x^{n}}$$

El logaritmo natural (con base e ) tiene serie de Maclaurin ^[13]

$${\displaystyle {\begin{aligned}\ln(1-x)&=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}=-x-{\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-\cdots ,\\\ln(1+x)&=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n}}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots .\end{aligned}}}$$

La última serie se conoce como serie de Mercator , llamada así por Nicholas Mercator (ya que fue publicada en su tratado de 1668 Logarithmotechnia ). ^[14] Ambas series convergen para . (Además, la serie para ln(1 − x ) converge para x = −1 , y la serie para ln(1 + x ) converge para x = 1 .) ^[13]${\displaystyle |x|<1}$

Las series geométricas y sus derivadas tienen serie de Maclaurin

$${\displaystyle {\begin{aligned}{\frac {1}{1-x}}&=\sum _{n=0}^{\infty }x^{n}\\{\frac {1}{(1-x)^{2}}}&=\sum _{n=1}^{\infty }nx^{n-1}\\{\frac {1}{(1-x)^{3}}}&=\sum _{n=2}^{\infty }{\frac {(n-1)n}{2}}x^{n-2}.\end{aligned}}}$$

Todas son convergentes para . Estos son casos especiales de la serie binomial que se dan en la siguiente sección.${\displaystyle |x|<1}$

La serie binomial es la serie de potencias

$${\displaystyle (1+x)^{\alpha }=\sum _{n=0}^{\infty }{\binom {\alpha }{n}}x^{n}}$$

cuyos coeficientes son los coeficientes binomiales generalizados ^[15]

$${\displaystyle {\binom {\alpha }{n}}=\prod _{k=1}^{n}{\frac {\alpha -k+1}{k}}={\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}.}$$

(Si n = 0 , este producto es un producto vacío y tiene valor 1). Converge para cualquier número real o complejo α .${\displaystyle |x|<1}$

Cuando α = −1 , se trata esencialmente de la serie geométrica infinita mencionada en la sección anterior. Los casos especiales α = ⁠1/2⁠ y α = − ⁠1/2⁠ da lafunción raíz cuadrada y su inversa : ^[16]

$${\displaystyle {\begin{aligned}(1+x)^{\frac {1}{2}}&=1+{\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+{\frac {7}{256}}x^{5}-\cdots &=\sum _{n=0}^{\infty }{\frac {(-1)^{n-1}(2n)!}{4^{n}(n!)^{2}(2n-1)}}x^{n},\\(1+x)^{-{\frac {1}{2}}}&=1-{\frac {1}{2}}x+{\frac {3}{8}}x^{2}-{\frac {5}{16}}x^{3}+{\frac {35}{128}}x^{4}-{\frac {63}{256}}x^{5}+\cdots &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}}}x^{n}.\end{aligned}}}$$

Cuando sólo se conserva el término lineal , esto se simplifica a la aproximación binomial .

Las funciones trigonométricas habituales y sus inversas tienen la siguiente serie de Maclaurin: ^[17]

$${\displaystyle {\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&{\text{for all }}x\\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}&&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&{\text{for all }}x\\[6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&{\text{for }}|x|\leq 1\\[6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2}}-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end{aligned}}}$$

Todos los ángulos se expresan en radianes . Los números B _k que aparecen en las expansiones de tan x son los números de Bernoulli . Los E _k en la expansión de sec x son los números de Euler . ^[18]

Las funciones hiperbólicas tienen series de Maclaurin estrechamente relacionadas con las series de las funciones trigonométricas correspondientes: ^[19]

$${\displaystyle {\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}&&=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots &&{\text{for all }}x\\[6pt]\cosh x&=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&&=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+\cdots &&{\text{for all }}x\\[6pt]\tanh x&=\sum _{n=1}^{\infty }{\frac {B_{2n}4^{n}\left(4^{n}-1\right)}{(2n)!}}x^{2n-1}&&=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\operatorname {arsinh} x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\operatorname {artanh} x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}&&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm 1\end{aligned}}}$$

Los números B _k que aparecen en la serie para tanh x son los números de Bernoulli . ^[19]

Los polilogaritmos tienen estas identidades definitorias:

$${\displaystyle {\begin{aligned}{\text{Li}}_{2}(x)&=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}x^{n}\\{\text{Li}}_{3}(x)&=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}x^{n}\end{aligned}}}$$

Las funciones chi de Legendre se definen de la siguiente manera:

$${\displaystyle {\begin{aligned}\chi _{2}(x)&=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)^{2}}}x^{2n+1}\\\chi _{3}(x)&=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)^{3}}}x^{2n+1}\end{aligned}}}$$

Y las fórmulas que se presentan a continuación se llaman integrales tangentes inversas :

$${\displaystyle {\begin{aligned}{\text{Ti}}_{2}(x)&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)^{2}}}x^{2n+1}\\{\text{Ti}}_{3}(x)&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)^{3}}}x^{2n+1}\end{aligned}}}$$

En termodinámica estadística estas fórmulas son de gran importancia.

Las integrales elípticas completas de primer tipo K y de segundo tipo E se pueden definir de la siguiente manera:

$${\displaystyle {\begin{aligned}{\frac {2}{\pi }}K(x)&=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{16^{n}(n!)^{4}}}x^{2n}\\{\frac {2}{\pi }}E(x)&=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{(1-2n)16^{n}(n!)^{4}}}x^{2n}\end{aligned}}}$$

Las funciones theta de Jacobi describen el mundo de las funciones modulares elípticas y tienen estas series de Taylor:

$${\displaystyle {\begin{aligned}\vartheta _{00}(x)&=1+2\sum _{n=1}^{\infty }x^{n^{2}}\\\vartheta _{01}(x)&=1+2\sum _{n=1}^{\infty }(-1)^{n}x^{n^{2}}\end{aligned}}}$$

La secuencia de números de partición regular P(n) tiene esta función generadora:

$${\displaystyle \vartheta _{00}(x)^{-1/6}\vartheta _{01}(x)^{-2/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}=\sum _{n=0}^{\infty }P(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{k}}}}$$

La secuencia de números de partición estricta Q(n) tiene esa función generadora:

$${\displaystyle \vartheta _{00}(x)^{1/6}\vartheta _{01}(x)^{-1/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}=\sum _{n=0}^{\infty }Q(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}}$$

Existen varios métodos para el cálculo de la serie de Taylor de un gran número de funciones. Se puede intentar utilizar la definición de la serie de Taylor, aunque esto a menudo requiere generalizar la forma de los coeficientes de acuerdo con un patrón fácilmente aparente. Alternativamente, se pueden utilizar manipulaciones como la sustitución, la multiplicación o la división, la suma o la resta de la serie de Taylor estándar para construir la serie de Taylor de una función, en virtud de que la serie de Taylor es una serie de potencias. En algunos casos, también se puede derivar la serie de Taylor aplicando repetidamente la integración por partes . Particularmente conveniente es el uso de sistemas de álgebra computacional para calcular la serie de Taylor.

Para calcular el polinomio de Maclaurin de séptimo grado para la función

$${\displaystyle f(x)=\ln(\cos x),\quad x\in {\bigl (}{-{\tfrac {\pi }{2}}},{\tfrac {\pi }{2}}{\bigr )},}$$

Primero se puede reescribir la función como

$${\displaystyle f(x)={\ln }{\bigl (}1+(\cos x-1){\bigr )},}$$

La composición de dos funciones y la serie de Taylor para el logaritmo natural es (usando la notación O grande )${\displaystyle x\mapsto \ln(1+x)}$${\displaystyle x\mapsto \cos x-1.}$

$${\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+O{\left(x^{4}\right)}}$$

y para la función coseno

$${\displaystyle \cos x-1=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}+O{\left(x^{8}\right)}.}$$

Los primeros términos de la segunda serie se pueden sustituir en cada término de la primera serie. Como el primer término de la segunda serie tiene grado 2, tres términos de la primera serie son suficientes para obtener un polinomio de séptimo grado:

$${\displaystyle {\begin{aligned}f(x)&=\ln {\bigl (}1+(\cos x-1){\bigr )}\\&=(\cos x-1)-{\tfrac {1}{2}}(\cos x-1)^{2}+{\tfrac {1}{3}}(\cos x-1)^{3}+O{\left((\cos x-1)^{4}\right)}\\&=-{\frac {x^{2}}{2}}-{\frac {x^{4}}{12}}-{\frac {x^{6}}{45}}+O{\left(x^{8}\right)}.\end{aligned}}\!}$$

Como el coseno es una función par , los coeficientes para todas las potencias impares son cero.

Supongamos que queremos la serie de Taylor en 0 de la función

$${\displaystyle g(x)={\frac {e^{x}}{\cos x}}.\!}$$

La serie de Taylor para la función exponencial es

$${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots ,}$$

y la serie para el coseno es

$${\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots .}$$

Supongamos que la serie para su cociente es

$${\displaystyle {\frac {e^{x}}{\cos x}}=c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4}+\cdots }$$

Multiplicando ambos lados por el denominador y luego expandiéndolo como una serie obtenemos${\displaystyle \cos x}$

$${\displaystyle {\begin{aligned}e^{x}&=\left(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4}+\cdots \right)\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots \right)\\[5mu]&=c_{0}+c_{1}x+\left(c_{2}-{\frac {c_{0}}{2}}\right)x^{2}+\left(c_{3}-{\frac {c_{1}}{2}}\right)x^{3}+\left(c_{4}-{\frac {c_{2}}{2}}+{\frac {c_{0}}{4!}}\right)x^{4}+\cdots \end{aligned}}}$$

Comparando los coeficientes de con los coeficientes de${\displaystyle g(x)\cos x}$${\displaystyle e^{x},}$

$${\displaystyle c_{0}=1,\ \ c_{1}=1,\ \ c_{2}-{\tfrac {1}{2}}c_{0}={\tfrac {1}{2}},\ \ c_{3}-{\tfrac {1}{2}}c_{1}={\tfrac {1}{6}},\ \ c_{4}-{\tfrac {1}{2}}c_{2}+{\tfrac {1}{24}}c_{0}={\tfrac {1}{24}},\ \ldots .}$$

Los coeficientes de la serie para se pueden calcular de a uno por vez, lo que equivale a una división larga de la serie para y :${\displaystyle c_{i}}$${\displaystyle g(x)}$${\displaystyle e^{x}}$${\displaystyle \cos x}$

$${\displaystyle {\frac {e^{x}}{\cos x}}=1+x+x^{2}+{\tfrac {2}{3}}x^{3}+{\tfrac {1}{2}}x^{4}+\cdots .}$$

Aquí empleamos un método llamado "expansión indirecta" para expandir la función dada. Este método utiliza la conocida expansión de Taylor de la función exponencial. Para expandir (1 + x ) e ^x como una serie de Taylor en x , utilizamos la conocida serie de Taylor de la función e ^x :

$${\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots .}$$

De este modo,

$${\displaystyle {\begin{aligned}(1+x)e^{x}&=e^{x}+xe^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}\\&=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=1}^{\infty }{\frac {x^{n}}{(n-1)!}}=1+\sum _{n=1}^{\infty }\left({\frac {1}{n!}}+{\frac {1}{(n-1)!}}\right)x^{n}\\&=1+\sum _{n=1}^{\infty }{\frac {n+1}{n!}}x^{n}\\&=\sum _{n=0}^{\infty }{\frac {n+1}{n!}}x^{n}.\end{aligned}}}$$

Clásicamente, las funciones algebraicas se definen mediante una ecuación algebraica, y las funciones trascendentales (incluidas las analizadas anteriormente) se definen mediante alguna propiedad que se cumple para ellas, como una ecuación diferencial . Por ejemplo, la función exponencial es la función que es igual a su propia derivada en todas partes y asume el valor 1 en el origen. Sin embargo, también se puede definir una función analítica mediante su serie de Taylor.

Las series de Taylor se utilizan para definir funciones y " operadores " en diversas áreas de las matemáticas. En particular, esto es cierto en áreas en las que las definiciones clásicas de funciones no funcionan. Por ejemplo, utilizando las series de Taylor, se pueden extender las funciones analíticas a conjuntos de matrices y operadores, como la matriz exponencial o la matriz logarítmica .

En otras áreas, como el análisis formal, resulta más conveniente trabajar directamente con las series de potencias . Así, se puede definir una solución de una ecuación diferencial como una serie de potencias que, se espera demostrar, es la serie de Taylor de la solución deseada.

La serie de Taylor también puede generalizarse a funciones de más de una variable con ^[20]

$${\displaystyle {\begin{aligned}T(x_{1},\ldots ,x_{d})&=\sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{d}=0}^{\infty }{\frac {(x_{1}-a_{1})^{n_{1}}\cdots (x_{d}-a_{d})^{n_{d}}}{n_{1}!\cdots n_{d}!}}\,\left({\frac {\partial ^{n_{1}+\cdots +n_{d}}f}{\partial x_{1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}\right)(a_{1},\ldots ,a_{d})\\&=f(a_{1},\ldots ,a_{d})+\sum _{j=1}^{d}{\frac {\partial f(a_{1},\ldots ,a_{d})}{\partial x_{j}}}(x_{j}-a_{j})+{\frac {1}{2!}}\sum _{j=1}^{d}\sum _{k=1}^{d}{\frac {\partial ^{2}f(a_{1},\ldots ,a_{d})}{\partial x_{j}\partial x_{k}}}(x_{j}-a_{j})(x_{k}-a_{k})\\&\qquad \qquad +{\frac {1}{3!}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{\frac {\partial ^{3}f(a_{1},\ldots ,a_{d})}{\partial x_{j}\partial x_{k}\partial x_{l}}}(x_{j}-a_{j})(x_{k}-a_{k})(x_{l}-a_{l})+\cdots \end{aligned}}}$$

Por ejemplo, para una función que depende de dos variables, x e y , la serie de Taylor de segundo orden respecto al punto ( a , b ) es${\displaystyle f(x,y)}$

$${\displaystyle f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)+{\frac {1}{2!}}{\Big (}(x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b){\Big )}}$$

donde los subíndices denotan las respectivas derivadas parciales .

Una expansión en serie de Taylor de segundo orden de una función escalar de más de una variable se puede escribir de manera compacta como

$${\displaystyle T(\mathbf {x} )=f(\mathbf {a} )+(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}Df(\mathbf {a} )+{\frac {1}{2!}}(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}\left\{D^{2}f(\mathbf {a} )\right\}(\mathbf {x} -\mathbf {a} )+\cdots ,}$$

donde D f  ( a ) es el gradiente de f evaluado en x = a y D ² f  ( a ) es la matriz hessiana . Aplicando la notación de índices múltiples, la serie de Taylor para varias variables se convierte en

$${\displaystyle T(\mathbf {x} )=\sum _{|\alpha |\geq 0}{\frac {(\mathbf {x} -\mathbf {a} )^{\alpha }}{\alpha !}}\left({\mathrm {\partial } ^{\alpha }}f\right)(\mathbf {a} ),}$$

lo cual debe entenderse como una versión multiíndice aún más abreviada de la primera ecuación de este párrafo, con una analogía completa con el caso de una sola variable.

Para calcular una expansión de la serie de Taylor de segundo orden alrededor del punto ( a , b ) = (0, 0) de la función$${\displaystyle f(x,y)=e^{x}\ln(1+y),}$$

Primero se calculan todas las derivadas parciales necesarias:

$${\displaystyle {\begin{aligned}f_{x}&=e^{x}\ln(1+y)\\[6pt]f_{y}&={\frac {e^{x}}{1+y}}\\[6pt]f_{xx}&=e^{x}\ln(1+y)\\[6pt]f_{yy}&=-{\frac {e^{x}}{(1+y)^{2}}}\\[6pt]f_{xy}&=f_{yx}={\frac {e^{x}}{1+y}}.\end{aligned}}}$$

Evaluando estas derivadas en el origen se obtienen los coeficientes de Taylor

$${\displaystyle {\begin{aligned}f_{x}(0,0)&=0\\f_{y}(0,0)&=1\\f_{xx}(0,0)&=0\\f_{yy}(0,0)&=-1\\f_{xy}(0,0)&=f_{yx}(0,0)=1.\end{aligned}}}$$

Sustituyendo estos valores en la fórmula general

$${\displaystyle {\begin{aligned}T(x,y)=&f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)\\&{}+{\frac {1}{2!}}\left((x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b)\right)+\cdots \end{aligned}}}$$

produce

$${\displaystyle {\begin{aligned}T(x,y)&=0+0(x-0)+1(y-0)+{\frac {1}{2}}{\big (}0(x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{\big )}+\cdots \\&=y+xy-{\tfrac {1}{2}}y^{2}+\cdots \end{aligned}}}$$

Como ln(1 + y ) es analítico en | y | < 1 , tenemos

$${\displaystyle e^{x}\ln(1+y)=y+xy-{\tfrac {1}{2}}y^{2}+\cdots ,\qquad |y|<1.}$$

La serie trigonométrica de Fourier permite expresar una función periódica (o una función definida en un intervalo cerrado [ a , b ] ) como una suma infinita de funciones trigonométricas ( senos y cosenos ). En este sentido, la serie de Fourier es análoga a la serie de Taylor, ya que esta última permite expresar una función como una suma infinita de potencias . Sin embargo, las dos series difieren entre sí en varias cuestiones relevantes:

• Los truncamientos finitos de la serie de Taylor de f  ( x ) respecto del punto x = a son todos exactamente iguales a f en a . Por el contrario, la serie de Fourier se calcula integrando sobre un intervalo entero, por lo que generalmente no existe un punto en el que todos los truncamientos finitos de la serie sean exactos.
• El cálculo de la serie de Taylor requiere el conocimiento de la función en un entorno arbitrario pequeño de un punto, mientras que el cálculo de la serie de Fourier requiere el conocimiento de la función en todo su intervalo de dominio . En cierto sentido, se podría decir que la serie de Taylor es "local" y la serie de Fourier es "global".
• La serie de Taylor se define para una función que tiene infinitas derivadas en un único punto, mientras que la serie de Fourier se define para cualquier función integrable . En particular, la función podría no ser diferenciable en ningún punto. (Por ejemplo, f  ( x ) podría ser una función de Weierstrass ).
• La convergencia de ambas series tiene propiedades muy diferentes. Incluso si la serie de Taylor tiene un radio de convergencia positivo, la serie resultante puede no coincidir con la función; pero si la función es analítica, entonces la serie converge puntualmente a la función y de manera uniforme en cada subconjunto compacto del intervalo de convergencia. En cuanto a la serie de Fourier, si la función es integrable al cuadrado , entonces la serie converge en media cuadrática , pero se necesitan requisitos adicionales para asegurar la convergencia puntual o uniforme (por ejemplo, si la función es periódica y de clase C ¹ , entonces la convergencia es uniforme).
• Por último, en la práctica se desea aproximar la función con un número finito de términos, por ejemplo, con un polinomio de Taylor o una suma parcial de la serie trigonométrica, respectivamente. En el caso de la serie de Taylor, el error es muy pequeño en las proximidades del punto en el que se calcula, mientras que puede ser muy grande en un punto distante. En el caso de la serie de Fourier, el error se distribuye a lo largo del dominio de la función.

• Expansión asintótica
• Polinomio de Newton
• Aproximación de Padé : la mejor aproximación mediante una función racional
• Serie de Puiseux  – Serie de potencias con exponentes racionales
• Teoría de aproximación
• Aproximación de funciones

• "Serie de Taylor", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Serie Taylor". MundoMatemático .