Geometría sólida
This article needs additional citations for verification. (May 2014) |

La geometría sólida o estereometría es la geometría del espacio euclidiano tridimensional (espacio 3D). [1] Una figura sólida es la región del espacio 3D delimitada por una superficie cerrada bidimensional ; por ejemplo, una bola sólida consta de una esfera y su interior .
La geometría sólida se ocupa de las mediciones de volúmenes de varios sólidos, incluidas pirámides , prismas (y otros poliedros ), cubos , cilindros , conos (y conos truncados ). [2]
Historia
Los pitagóricos se ocuparon de los sólidos regulares , pero la pirámide, el prisma, el cono y el cilindro no fueron estudiados hasta los platónicos . Eudoxo estableció su medida, demostrando que la pirámide y el cono tienen un tercio del volumen de un prisma y un cilindro sobre la misma base y de la misma altura. Probablemente también fue el descubridor de una prueba de que el volumen encerrado por una esfera es proporcional al cubo de su radio . [3]
Temas
Los temas básicos en geometría sólida y estereometría incluyen:
- incidencia de planos y lineas
- ángulo diedro y ángulo sólido
- el cubo , cuboide , paralelepípedo
- El tetraedro y otras pirámides
- prismas
- octaedro , dodecaedro , icosaedro
- conos y cilindros
- La esfera
- otras cuádricas : esferoide , elipsoide , paraboloide e hiperboloides .
- Geometría plana vs geometría sólida
Los temas avanzados incluyen:
- Geometría proyectiva de tres dimensiones (que conduce a una prueba del teorema de Desargues utilizando una dimensión adicional)
- otros poliedros
- geometría descriptiva .
Lista de figuras sólidas
Mientras que una esfera es la superficie de una bola , para otras figuras sólidas a veces es ambiguo si el término se refiere a la superficie de la figura o al volumen encerrado en ella, en particular para un cilindro .
| Cifra | Definiciones | Imágenes | |
|---|---|---|---|
| Paralelepípedo |
| 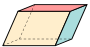 | |
| Romboedro |
|  | |
| Cuboides |
|  | |
| Poliedro | Caras poligonales planas , aristas rectas y esquinas o vértices agudos |  Pequeño dodecaedro estrellado |  Poliedro toroidal |
| Poliedro uniforme | Los polígonos regulares son caras y son transitivos en función de los vértices (es decir, existe una isometría que asigna cualquier vértice a cualquier otro). |   Tetraedro (regular) y cubo |  Dodecaedro romo no formado |
| Pirámide | Un poliedro que comprende una base poligonal de n lados y un punto de vértice. |  pirámide cuadrada pirámide cuadrada | |
| Prisma | Un poliedro que comprende una base poligonal de n lados , una segunda base que es una copia trasladada (movida rígidamente sin rotación) de la primera y n caras más (necesariamente todas paralelas ) que unen los lados correspondientes de las dos bases. |  prisma hexagonal prisma hexagonal | |
| Antiprisma | Un poliedro que comprende una base poligonal de n lados , una segunda base trasladada y rotada.lados]] de las dos bases |  antiprisma cuadrado antiprisma cuadrado | |
| Bipirámide | Un poliedro que comprende un centro poligonal de n lados con dos vértices. |  bipirámide triangular bipirámide triangular | |
| Trapezoedro | Un poliedro con 2 n caras de cometa alrededor de un eje, con desplazamientos a la mitad |  trapezoedro tetragonal trapezoedro tetragonal | |
| Cono | Se estrecha suavemente desde una base plana (con frecuencia, aunque no necesariamente, circular) hasta un punto llamado ápice o vértice. |  Un cono circular recto y un cono circular oblicuo | |
| Cilindro | Lados rectos paralelos y sección transversal circular u ovalada. |  Un cilindro elíptico sólido |  Un cilindro circular recto y uno oblicuo |
| Elipsoide | Superficie que puede obtenerse a partir de una esfera deformándola mediante escalas direccionales o, más generalmente, mediante una transformación afín . |  Ejemplos de elipsoides | esfera (arriba, a=b=c=4), esferoide (abajo a la izquierda, a=b=5, c=3), |
| Limón | Una lente (o menos de la mitad de un arco circular) girada alrededor de un eje que pasa por los puntos finales de la lente (o arco) [6] |  | |
| Hiperboloide | Una superficie que se genera al rotar una hipérbola alrededor de uno de sus ejes principales. |  | |
Técnicas
En la geometría de sólidos se utilizan diversas técnicas y herramientas. Entre ellas, la geometría analítica y las técnicas vectoriales tienen un gran impacto al permitir el uso sistemático de ecuaciones lineales y álgebra matricial , importantes para dimensiones superiores.
Aplicaciones
Una aplicación importante de la geometría sólida y la estereometría es en los gráficos de computadora en 3D .
Véase también
Notas
- ^ La guía británica de geometría , Britannica Educational Publishing, 2010, págs. 67–68.
- ^ Kiselev 2008.
- ^ Parafraseado y tomado en parte de la Enciclopedia Británica de 1911 .
- ^ Robertson, Stewart Alexander (1984). Politopos y simetría . Cambridge University Press. pág. 75. ISBN 9780521277396.
- ^ Dupuis, Nathan Fellowes (1893). Elementos de geometría sólida sintética. Macmillan. pág. 53. Consultado el 1 de diciembre de 2018 .
- ^ Weisstein, Eric W. "Limón". Wolfram MathWorld . Consultado el 4 de noviembre de 2019 .
Referencias
- Kiselev, AP (2008). Geometría . Vol. Libro II. Estereometría. Traducido por Givental, Alexander. Sumizdat.

