Arrastre (física)

En dinámica de fluidos , la resistencia al avance , a veces denominada resistencia del fluido , es una fuerza que actúa en sentido opuesto al movimiento relativo de cualquier objeto que se mueva con respecto a un fluido circundante . ^[1] Esto puede existir entre dos capas de fluido, dos superficies sólidas o entre un fluido y una superficie sólida. Las fuerzas de arrastre tienden a disminuir la velocidad del fluido en relación con el objeto sólido en la trayectoria del fluido.

A diferencia de otras fuerzas resistivas, la fuerza de arrastre depende de la velocidad. ^{[2] [3]} Esto se debe a que la fuerza de arrastre es proporcional a la velocidad para el flujo de baja velocidad y al cuadrado de la velocidad para el flujo de alta velocidad. Esta distinción entre flujo de baja y alta velocidad se mide mediante el número de Reynolds .

Algunos ejemplos de arrastre incluyen:

• Fuerza aerodinámica o hidrodinámica neta : Resistencia que actúa en dirección opuesta al movimiento de un objeto sólido, como automóviles, aviones ^[3] y cascos de barcos.

• Arrastre viscoso del fluido en una tubería : la fuerza de arrastre sobre la tubería inmóvil disminuye la velocidad del fluido con respecto a la tubería. ^{[4] [5]}

• En la física de los deportes, la fuerza de arrastre es necesaria para explicar el movimiento de pelotas, jabalinas, flechas y frisbees, así como el rendimiento de corredores y nadadores. ^[6] Para un velocista de alto nivel, superar la resistencia puede requerir el 5% de su gasto energético. ^[7]

Forma y flujo	Arrastre de formulario	Fricción de la piel
	≈0%	≈100%
	≈10%	≈90%
	≈90%	≈10%
	≈100%	≈0%

Los tipos de arrastre generalmente se dividen en las siguientes categorías:

• Arrastre de forma o arrastre de presión debido al tamaño y la forma de un cuerpo
• Arrastre por fricción de la piel o arrastre viscoso debido a la fricción entre el fluido y una superficie que puede ser el exterior de un objeto o el interior, como el orificio de una tubería.

Se muestra el efecto de la aerodinámica en las proporciones relativas de fricción superficial y resistencia de forma para dos secciones de carrocería diferentes: un perfil aerodinámico, que es una carrocería aerodinámica, y un cilindro, que es una carrocería con forma de romo. También se muestra una placa plana que ilustra el efecto que tiene la orientación en las proporciones relativas de fricción superficial y la diferencia de presión entre la parte delantera y la trasera.

Un cuerpo se conoce como romo o desafilado cuando la fuente de arrastre está dominada por fuerzas de presión, y aerodinámico si el arrastre está dominado por fuerzas viscosas. Por ejemplo, los vehículos de carretera son cuerpos romos. ^[8] Para las aeronaves, la presión y el arrastre por fricción se incluyen en la definición de arrastre parásito . El arrastre parásito a menudo se expresa en términos de una hipótesis.

Esta es el área de una placa plana perpendicular al flujo. Se utiliza al comparar la resistencia de diferentes aeronaves. Por ejemplo, el Douglas DC-3 tiene un área parásita equivalente de 2,20 m ² (23,7 pies cuadrados) y el McDonnell Douglas DC-9 , con 30 años de avance en el diseño de aeronaves, un área de 1,91 m ² (20,6 pies cuadrados) aunque transportaba cinco veces más pasajeros. ^[9]

• La resistencia inducida por sustentación aparece con alas o un cuerpo sustentador en la aviación y con cascos de semiplaneo o planeo en las embarcaciones.
• La resistencia de las ondas ( aerodinámica ) es causada por la presencia de ondas de choque y aparece por primera vez a velocidades subsónicas de la aeronave, cuando las velocidades de flujo locales se vuelven supersónicas. La resistencia de las ondas del prototipo supersónico del avión Concorde se redujo a Mach 2 en un 1,8 % mediante la aplicación de la regla del área que extendió el fuselaje trasero 3,73 m (12,2 pies) en el avión de producción. ^[10]
• La resistencia de las olas (hidrodinámica del barco) o arrastre de las olas ocurre cuando un objeto sólido se mueve a lo largo de un límite de fluido y genera ondas superficiales .
• La resistencia de la cola del barco en una aeronave es causada por el ángulo con el que el fuselaje trasero, o la góndola del motor, se estrecha hacia el diámetro de escape del motor. ^[11]

• 
  Concorde con cola de arrastre de olas 'alta'
• 
  Concorde con cola de arrastre de onda 'baja' (NB: punta del fuselaje trasero)
• 
  Avión Hawk que muestra el área de la base sobre el escape circular del motor

La resistencia inducida por sustentación (también llamada resistencia inducida ) es la resistencia que se produce como resultado de la creación de sustentación en un cuerpo sustentador tridimensional , como el ala o la hélice de un avión. La resistencia inducida consta principalmente de dos componentes: la resistencia debida a la creación de vórtices de cola ( resistencia de vórtice ); y la presencia de resistencia viscosa adicional ( resistencia viscosa inducida por sustentación ) que no está presente cuando la sustentación es cero. Los vórtices de cola en el campo de flujo, presentes en la estela de un cuerpo sustentador, se derivan de la mezcla turbulenta de aire desde arriba y desde abajo del cuerpo que fluye en direcciones ligeramente diferentes como consecuencia de la creación de sustentación .

Si los demás parámetros se mantienen constantes, a medida que aumenta la sustentación generada por un cuerpo, también aumenta la resistencia inducida por la sustentación. Esto significa que, a medida que aumenta el ángulo de ataque del ala (hasta un máximo llamado ángulo de pérdida), el coeficiente de sustentación también aumenta, y también lo hace la resistencia inducida por la sustentación. Al comienzo de la pérdida , la sustentación disminuye abruptamente, al igual que la resistencia inducida por la sustentación, pero la resistencia por presión viscosa, un componente de la resistencia parásita, aumenta debido a la formación de flujo turbulento no adherido en la estela detrás del cuerpo.

La resistencia parasitaria , o resistencia de perfil, es la resistencia causada por el movimiento de un objeto sólido a través de un fluido. La resistencia parasitaria está formada por múltiples componentes, entre ellos la resistencia por presión viscosa ( resistencia por forma ) y la resistencia debida a la rugosidad de la superficie ( resistencia por fricción superficial ). Además, la presencia de múltiples cuerpos en relativa proximidad puede generar la denominada resistencia por interferencia , que a veces se describe como un componente de la resistencia parasitaria.

En aviación, la resistencia inducida tiende a ser mayor a velocidades más bajas porque se requiere un ángulo de ataque alto para mantener la sustentación, lo que crea más resistencia. Sin embargo, a medida que aumenta la velocidad, el ángulo de ataque se puede reducir y la resistencia inducida disminuye. La resistencia parásita, sin embargo, aumenta porque el fluido fluye más rápidamente alrededor de objetos que sobresalen, lo que aumenta la fricción o la resistencia. A velocidades aún más altas ( transónicas ), entra en escena la resistencia ondulatoria . Cada una de estas formas de resistencia cambia en proporción a las demás en función de la velocidad. Por lo tanto, la curva de resistencia general combinada muestra un mínimo a cierta velocidad aerodinámica: un avión que vuela a esta velocidad estará en o cerca de su eficiencia óptima. Los pilotos usarán esta velocidad para maximizar la resistencia (consumo mínimo de combustible) o maximizar el rango de planeo en caso de una falla del motor.

La resistencia depende de las propiedades del fluido y del tamaño, la forma y la velocidad del objeto. Una forma de expresar esto es mediante la ecuación de resistencia : donde$${\displaystyle F_{\mathrm {D} }\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{\mathrm {D} }\,A }$$

• $Estilo de visualización F_{\rm {D}}}$es la fuerza de arrastre ,
• ${\estilo de visualización \rho}$es la densidad del fluido, ^[12]
• ${\estilo de visualización v}$es la velocidad del objeto en relación con el fluido,
• ${\estilo de visualización A}$es el área de la sección transversal , y
• $Estilo de visualización C_{\rm {D}}}$es el coeficiente de arrastre , un número adimensional .

El coeficiente de arrastre depende de la forma del objeto y del número de Reynolds , donde$${\displaystyle \mathrm {Re} ={\frac {vD}{\nu }}={\frac {\rho vD}{\mu }},}$$

• ${\estilo de visualización D}$es un diámetro característico o una dimensión lineal . En realidad, es el diámetro equivalente del objeto. Para una esfera, es el D de la esfera misma.${\estilo de visualización D}$ ${\displaystyle D_{e}}$${\displaystyle D_{e}}$
• Para una sección transversal de forma rectangular en la dirección del movimiento, , donde a y b son los bordes del rectángulo.${\displaystyle D_{e}=1.30\cdot {\frac {(a\cdot b)^{0.625}}{(a+b)^{0.25}}}}$
• ${\displaystyle {\nu}}$es la viscosidad cinemática del fluido (igual a la viscosidad dinámica dividida por la densidad ).${\estilo de visualización {\mu}}$${\estilo de visualización {\rho}}$

En un nivel bajo , es asintóticamente proporcional a , lo que significa que la resistencia es linealmente proporcional a la velocidad, es decir, la fuerza de resistencia sobre una esfera pequeña que se mueve a través de un fluido viscoso está dada por la Ley de Stokes : En un nivel alto , es más o menos constante, pero la resistencia variará a medida que varía el cuadrado de la velocidad. El gráfico de la derecha muestra cómo varía con para el caso de una esfera. Dado que la potencia necesaria para vencer la fuerza de resistencia es el producto de la fuerza por la velocidad, la potencia necesaria para vencer la resistencia variará como el cuadrado de la velocidad en números de Reynolds bajos y como el cubo de la velocidad en números altos.${\displaystyle \mathrm {Re}}$$Estilo de visualización C_{\rm {D}}}$${\displaystyle \mathrm {Re} ^{-1}}$$${\displaystyle F_{\rm {d}}=3\pi \mu Dv}$$${\displaystyle \mathrm {Re}}$$Estilo de visualización C_{\rm {D}}}$$Estilo de visualización C_{\rm {D}}}$${\displaystyle \mathrm {Re}}$

Se puede demostrar que la fuerza de arrastre se puede expresar como una función de un número adimensional, que es dimensionalmente idéntico al número de Bejan . ^[13] En consecuencia, la fuerza de arrastre y el coeficiente de arrastre pueden ser una función del número de Bejan. De hecho, a partir de la expresión de la fuerza de arrastre se ha obtenido: y en consecuencia permite expresar el coeficiente de arrastre como una función del número de Bejan y la relación entre el área húmeda y el área frontal : ^[13] donde es el número de Reynolds relacionado con la longitud del recorrido del fluido L.$${\displaystyle F_{\rm {d}}=\Delta _{\rm {p}}A_{\rm {w}}={\frac {1}{2}}C_{\rm {D}}A_{\rm {f}}{\frac {\nu \mu }{l^{2}}}\mathrm {Re} _{L}^{2}}$$ $Estilo de visualización C_{\rm {D}}}$$Estilo de visualización A_{\rm {w}}}$$Estilo de visualización A_{\rm {f}}}$$${\displaystyle C_{\rm {D}}=2{\frac {A_{\rm {w}}}{A_{\rm {f}}}}{\frac {\mathrm {Be} }{\mathrm {Re} _{L}^{2}}}}$$${\displaystyle \mathrm {Re} _ {L}}$

Como se mencionó, la ecuación de arrastre con un coeficiente de arrastre constante le da a la fuerza que se mueve a través del fluido una velocidad relativamente grande, es decir, un número de Reynolds alto , Re > ~1000. Esto también se llama arrastre cuadrático .

$${\displaystyle F_{D}\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{D}\,A,}$$La derivación de esta ecuación se presenta en Ecuación de arrastre § Derivación .

El área de referencia A es a menudo la proyección ortográfica del objeto, o el área frontal, sobre un plano perpendicular a la dirección del movimiento. Para objetos con una forma simple, como una esfera, esta es el área de la sección transversal . A veces, un cuerpo está compuesto de diferentes partes, cada una con un área de referencia diferente (se debe determinar el coeficiente de arrastre correspondiente a cada una de esas diferentes áreas).

En el caso de un ala , las áreas de referencia son las mismas y la fuerza de arrastre está en la misma proporción que la fuerza de sustentación . ^[14] Por lo tanto, la referencia para un ala es a menudo el área de sustentación, a veces denominada "área del ala" en lugar del área frontal. ^[15]

Para un objeto con una superficie lisa y puntos de separación no fijos (como una esfera o un cilindro circular), el coeficiente de arrastre puede variar con el número de Reynolds Re , hasta valores extremadamente altos ( Re del orden de 10 ⁷ ). ^{[16] [17]}

Para un objeto con puntos de separación fijos bien definidos, como un disco circular con su plano normal a la dirección del flujo, el coeficiente de arrastre es constante para Re  > 3500. ^[17] Cuanto más lejos esté el coeficiente de arrastre C _d , en general, será una función de la orientación del flujo con respecto al objeto (aparte de los objetos simétricos como una esfera).

Suponiendo que el fluido no se mueve con respecto al sistema de referencia utilizado actualmente, la potencia necesaria para superar la resistencia aerodinámica viene dada por: La potencia necesaria para empujar un objeto a través de un fluido aumenta a medida que aumenta el cubo de la velocidad. Por ejemplo, un coche que circula por una autopista a 50 mph (80 km/h) puede requerir solo 10 caballos de fuerza (7,5 kW) para superar la resistencia aerodinámica, pero ese mismo coche a 100 mph (160 km/h) requiere 80 caballos de fuerza (60 kW). ^[18] Con una duplicación de velocidades, la resistencia/fuerza se cuadruplica según la fórmula. Ejercer 4 veces la fuerza sobre una distancia fija produce 4 veces más trabajo . Al doble de velocidad, el trabajo (que resulta en el desplazamiento sobre una distancia fija) se realiza el doble de rápido. Dado que la potencia es la tasa de realización del trabajo, 4 veces el trabajo realizado en la mitad del tiempo requiere 8 veces la potencia.$${\displaystyle P_{D}=\mathbf {F} _{D}\cdot \mathbf {v} ={\tfrac {1}{2}}\rho v^{3}AC_{D}}$$

Cuando el fluido se mueve con respecto al sistema de referencia, por ejemplo, un automóvil que circula con viento en contra, la potencia necesaria para superar la resistencia aerodinámica viene dada por la siguiente fórmula:$${\displaystyle P_{D}=\mathbf {F} _{D}\cdot \mathbf {v_{o}} ={\tfrac {1}{2}}C_{D}A\rho (v_{w} +v_{o})^{2}v_{o}}$$

¿Dónde está la velocidad del viento y es la velocidad del objeto (ambas relativas al suelo)?$Estilo de visualización v_ {w}$${\displaystyle v_{o}}$

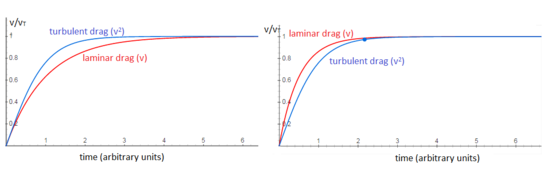
La velocidad en función del tiempo para un objeto que cae a través de un medio no denso y se libera a una velocidad relativa cero v  = 0 en el tiempo t  = 0, está dada aproximadamente por una función que involucra una tangente hiperbólica (tanh):$${\displaystyle v(t)={\sqrt {\frac {2mg}{\rho AC_{D}}}}\tanh \left(t{\sqrt {\frac {g\rho C_{D}A}{2m}}}\right).\,}$$

La tangente hiperbólica tiene un valor límite de uno para un tiempo grande t . En otras palabras, la velocidad se aproxima asintóticamente a un valor máximo llamado velocidad terminal v _t :$${\displaystyle v_{t}={\sqrt {\frac {2mg}{\rho AC_{D}}}}.\,}$$

Para un objeto que cae y se libera a una velocidad relativa v  = v _i en el tiempo t  = 0, con v _i < v _t , también se define en términos de la función tangente hiperbólica:$${\displaystyle v(t)=v_{t}\tanh \left(t{\frac {g}{v_{t}}}+\operatorname {arctanh} \left({\frac {v_{i}}{v_{t}}}\right)\right).\,}$$

Para v _i > v _t , la función de velocidad se define en términos de la función cotangente hiperbólica :$${\displaystyle v(t)=v_{t}\coth \left(t{\frac {g}{v_{t}}}+\coth ^{-1}\left({\frac {v_{i}}{v_{t}}}\right)\right).\,}$$

La cotangente hiperbólica también tiene un valor límite de uno, para un tiempo grande t . La velocidad tiende asintóticamente a la velocidad terminal v _t , estrictamente desde arriba de v _t .

Para v _i = v _t , la velocidad es constante:$${\displaystyle v(t)=v_{t}.}$$

Estas funciones se definen mediante la solución de la siguiente ecuación diferencial :$${\displaystyle g-{\frac {\rho AC_{D}}{2m}}v^{2}={\frac {dv}{dt}}.\,}$$

O, de manera más genérica (donde F ( v ) son las fuerzas que actúan sobre el objeto más allá del arrastre):$${\displaystyle {\frac {1}{m}}\suma F(v)-{\frac {\rho AC_{D}}{2m}}v^{2}={\frac {dv}{dt}}.\,}$$

Para un objeto con forma de papa de diámetro promedio d y densidad ρ _obj , la velocidad terminal es aproximadamente$${\displaystyle v_{t}={\sqrt {gd{\frac {\rho _{obj}}{\rho }}}}.\,}$$

Para objetos de densidad similar a la del agua (gotas de lluvia, granizo, objetos vivos: mamíferos, pájaros, insectos, etc.) que caen en el aire cerca de la superficie de la Tierra al nivel del mar, la velocidad terminal es aproximadamente igual a con d en metros y v _t en m/s. Por ejemplo, para un cuerpo humano ( ≈0,6 m) ≈70 m/s, para un animal pequeño como un gato ( ≈0,2 m) ≈40 m/s, para un pájaro pequeño ( ≈0,05 m) ≈20 m/s, para un insecto ( ≈0,01 m) ≈9 m/s, y así sucesivamente. La velocidad terminal para objetos muy pequeños (polen, etc.) a números de Reynolds bajos está determinada por la ley de Stokes.$${\displaystyle v_{t}=90{\sqrt {d}},\,}$$${\estilo de visualización d}$$estilo de visualización v_{t}}$${\estilo de visualización d}$$estilo de visualización v_{t}}$${\estilo de visualización d}$$estilo de visualización v_{t}}$${\estilo de visualización d}$$estilo de visualización v_{t}}$

En resumen, la velocidad terminal es mayor para las criaturas más grandes y, por lo tanto, potencialmente más mortal. Una criatura como un ratón que cae a su velocidad terminal tiene muchas más probabilidades de sobrevivir al impacto contra el suelo que un humano que cae a su velocidad terminal. ^[19]

La ecuación de resistencia viscosa o arrastre lineal es apropiada para objetos o partículas que se mueven a través de un fluido a velocidades relativamente bajas (suponiendo que no hay turbulencia). El flujo puramente laminar solo existe hasta Re = 0,1 según esta definición. En este caso, la fuerza de arrastre es aproximadamente proporcional a la velocidad. La ecuación de resistencia viscosa es: ^[20]

$${\displaystyle \mathbf {F} _{D}=-b\mathbf {v} \,}$$

dónde:

• ${\estilo de visualización b}$es una constante que depende tanto de las propiedades materiales del objeto y del fluido, como de la geometría del objeto; y
• ${\displaystyle \mathbf {v}}$es la velocidad del objeto.

Cuando un objeto cae desde el reposo, su velocidad será donde:$${\displaystyle v(t)={\frac {(\rho -\rho _{0})\,V\,g}{b}}\left(1-e^{-b\,t/m}\right)}$$

• ${\estilo de visualización \rho}$es la densidad del objeto,
• ${\displaystyle \rho_{0}}$es la densidad del fluido,
• ${\estilo de visualización V}$es el volumen del objeto,
• ${\estilo de visualización g}$es la aceleración debida a la gravedad (es decir, 9,8 m/s ), y${\estilo de visualización ^{2}}$
• ${\estilo de visualización m}$es la masa del objeto.

La velocidad se aproxima asintóticamente a la velocidad terminal . Para un valor dado , los objetos más densos caen más rápidamente.${\displaystyle v_{t}={\frac {(\rho -\rho _{0})Vg}{b}}}$${\estilo de visualización b}$

Para el caso especial de pequeños objetos esféricos que se mueven lentamente a través de un fluido viscoso (y, por lo tanto, con un pequeño número de Reynolds), George Gabriel Stokes derivó una expresión para la constante de arrastre: donde es el radio de Stokes de la partícula y es la viscosidad del fluido .$${\displaystyle b=6\pi \eta r\,}$$${\displaystyle r}$${\displaystyle \eta }$

La expresión resultante para la resistencia se conoce como resistencia de Stokes : ^[21]$${\displaystyle \mathbf {F} _{D}=-6\pi \eta r\,\mathbf {v} .}$$

Por ejemplo, supongamos que una esfera pequeña con un radio de 0,5 micrómetros (diámetro de 1,0 μm) se mueve a través del agua a una velocidad de 10 μm/s. Si utilizamos 10 ⁻³ Pa·s como la viscosidad dinámica del agua en unidades del SI, obtenemos una fuerza de arrastre de 0,09 pN. Esta es aproximadamente la fuerza de arrastre que experimenta una bacteria cuando nada en el agua.${\displaystyle r}$${\displaystyle v}$

El coeficiente de arrastre de una esfera se puede determinar para el caso general de un flujo laminar con números de Reynolds menores que utilizando la siguiente fórmula: ^[22]${\displaystyle 2\cdot 10^{5}}$

$${\displaystyle C_{D}={\frac {24}{Re}}+{\frac {4}{\sqrt {Re}}}+0.4~{\text{;}}~~~~~Re<2\cdot 10^{5}}$$

Para números de Reynolds menores que 1, se aplica la ley de Stokes y el coeficiente de arrastre se aproxima a !${\displaystyle {\frac {24}{Re}}}$

En aerodinámica , la resistencia aerodinámica , también conocida como resistencia del aire , es la fuerza de arrastre del fluido que actúa sobre cualquier cuerpo sólido en movimiento en la dirección del flujo libre del aire . ^[23]

• Desde la perspectiva del cuerpo (enfoque de campo cercano), la resistencia resulta de las fuerzas debidas a las distribuciones de presión sobre la superficie del cuerpo, simbolizadas .${\displaystyle D_{pr}}$
• Fuerzas debidas a la fricción de la piel, que es resultado de la viscosidad, denotadas .${\displaystyle D_{f}}$

Alternativamente, calculada desde la perspectiva del campo de flujo (enfoque de campo lejano), la fuerza de arrastre resulta de tres fenómenos naturales: ondas de choque , lámina de vórtice y viscosidad .

Cuando el avión produce sustentación, se produce otro componente de resistencia. La resistencia inducida , simbolizada , se debe a una modificación de la distribución de la presión debido al sistema de vórtices de cola que acompaña a la producción de sustentación. Se obtiene una perspectiva alternativa sobre la sustentación y la resistencia al considerar el cambio de momento del flujo de aire. El ala intercepta el flujo de aire y lo obliga a moverse hacia abajo. Esto da como resultado una fuerza igual y opuesta que actúa hacia arriba sobre el ala, que es la fuerza de sustentación. El cambio de momento del flujo de aire hacia abajo da como resultado una reducción del momento hacia atrás del flujo, que es el resultado de una fuerza que actúa hacia adelante sobre el flujo de aire y que el ala aplica al flujo de aire; una fuerza igual pero opuesta actúa sobre el ala hacia atrás, que es la resistencia inducida. Otro componente de resistencia, a saber, la resistencia de onda , resulta de las ondas de choque en velocidades de vuelo transónicas y supersónicas. Las ondas de choque inducen cambios en la capa límite y la distribución de la presión sobre la superficie del cuerpo.${\displaystyle D_{i}}$${\displaystyle D_{w}}$

Por lo tanto, hay tres formas de categorizar el arrastre. ^{[24] : 19}

1. Arrastre por presión y arrastre por fricción
2. Arrastre de perfil y arrastre inducido
3. Arrastre de vórtice, arrastre de ola y arrastre de estela

La distribución de presión que actúa sobre la superficie de un cuerpo ejerce fuerzas normales sobre el cuerpo. Esas fuerzas se pueden sumar y el componente de esa fuerza que actúa aguas abajo representa la fuerza de arrastre. La naturaleza de estas fuerzas normales combina efectos de ondas de choque, efectos de generación de sistemas de vórtices y mecanismos viscosos de estela.${\displaystyle D_{pr}}$

La viscosidad del fluido tiene un efecto importante en la resistencia. En ausencia de viscosidad, las fuerzas de presión que actúan para obstaculizar el vehículo se cancelan con una fuerza de presión situada más atrás que actúa para empujar el vehículo hacia adelante; esto se llama recuperación de presión y el resultado es que la resistencia es cero. Es decir, el trabajo que realiza la carrocería sobre el flujo de aire es reversible y se recupera ya que no hay efectos de fricción que conviertan la energía del flujo en calor. La recuperación de presión actúa incluso en el caso de flujo viscoso. Sin embargo, la viscosidad produce resistencia por presión y es el componente dominante de la resistencia en el caso de vehículos con regiones de flujo separado, en los que la recuperación de presión es infecciosa.

La fuerza de fricción, que es una fuerza tangencial sobre la superficie de la aeronave, depende sustancialmente de la configuración de la capa límite y de la viscosidad. La fricción neta, , se calcula como la proyección descendente de las fuerzas viscosas evaluadas sobre la superficie del cuerpo. La suma de la fricción y la presión (forma) se denomina fricción viscosa. Este componente de fricción se debe a la viscosidad. ${\displaystyle D_{f}}$

La idea de que un cuerpo en movimiento que pasa a través del aire u otro fluido encuentra resistencia se conocía desde la época de Aristóteles . Según Mervyn O'Gorman , Archibald Reith Low la denominó "resistencia" . ^[25] El artículo de Louis Charles Breguet de 1922 inició los esfuerzos para reducir la resistencia mediante la aerodinámica. ^[26] Breguet continuó poniendo en práctica sus ideas al diseñar varios aviones que batieron récords en las décadas de 1920 y 1930. La teoría de la capa límite de Ludwig Prandtl en la década de 1920 proporcionó el impulso para minimizar la fricción de la piel. Otro llamado importante a la aerodinámica fue realizado por Sir Melvill Jones , quien proporcionó los conceptos teóricos para demostrar enfáticamente la importancia de la aerodinámica en el diseño de aeronaves . ^{[27] [28] [29]} En 1929, su artículo 'The Streamline Airplane' presentado a la Royal Aeronautical Society fue seminal. Propuso un avión ideal que tendría una resistencia mínima, lo que condujo a los conceptos de un monoplano "limpio" y un tren de aterrizaje retráctil . El aspecto del trabajo de Jones que más sorprendió a los diseñadores de la época fue su gráfico de la potencia requerida en caballos de fuerza en función de la velocidad, para un avión real y uno ideal. Al observar un punto de datos para un avión determinado y extrapolándolo horizontalmente a la curva ideal, se puede ver la ganancia de velocidad para la misma potencia. Cuando Jones terminó su presentación, un miembro de la audiencia describió los resultados como del mismo nivel de importancia que el ciclo de Carnot en termodinámica. ^{[26] [27]}

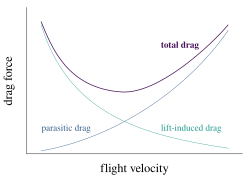
La interacción de la resistencia parásita e inducida frente a la velocidad aerodinámica se puede representar gráficamente como una curva característica, que se ilustra aquí. En aviación, a menudo se la denomina curva de potencia y es importante para los pilotos porque muestra que, por debajo de una determinada velocidad aerodinámica, mantener la velocidad aerodinámica, contrariamente a lo que se podría pensar, requiere más empuje a medida que disminuye la velocidad, en lugar de menos. Las consecuencias de estar "detrás de la curva" en vuelo son importantes y se enseñan como parte del entrenamiento de los pilotos. A velocidades aerodinámicas subsónicas, donde la forma de "U" de esta curva es significativa, la resistencia de las olas aún no se ha convertido en un factor, por lo que no se muestra en la curva.

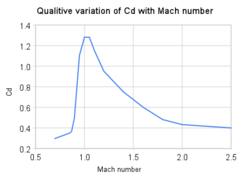
La resistencia de las olas, a veces denominada resistencia de compresibilidad, es la resistencia que se crea cuando un cuerpo se mueve en un fluido compresible y a una velocidad cercana a la velocidad del sonido en ese fluido. En aerodinámica , la resistencia de las olas consta de múltiples componentes que dependen del régimen de velocidad del vuelo.

En el vuelo transónico, la resistencia de las ondas es el resultado de la formación de ondas de choque en el fluido, que se forman cuando se crean áreas locales de flujo supersónico (número de Mach mayor que 1.0). En la práctica, el flujo supersónico se produce en cuerpos que viajan muy por debajo de la velocidad del sonido, ya que la velocidad local del aire aumenta a medida que acelera sobre el cuerpo a velocidades superiores a Mach 1.0. Sin embargo, el flujo supersónico completo sobre el vehículo no se desarrollará hasta mucho después de Mach 1.0. Las aeronaves que vuelan a velocidad transónica a menudo incurren en resistencia de las ondas durante el curso normal de la operación. En el vuelo transónico, la resistencia de las ondas se conoce comúnmente como resistencia de compresibilidad transónica . La resistencia de compresibilidad transónica aumenta significativamente a medida que la velocidad de vuelo aumenta hacia Mach 1.0, dominando otras formas de resistencia a esas velocidades.

En vuelo supersónico (números de Mach mayores que 1.0), la resistencia de onda es el resultado de ondas de choque presentes en el fluido y adheridas al cuerpo, típicamente ondas de choque oblicuas formadas en los bordes de entrada y salida del cuerpo. En flujos altamente supersónicos, o en cuerpos con ángulos de giro suficientemente grandes, se formarán en su lugar ondas de choque no adheridas u ondas de proa . Además, pueden ocurrir áreas locales de flujo transónico detrás de la onda de choque inicial a velocidades supersónicas más bajas, y pueden conducir al desarrollo de ondas de choque adicionales, más pequeñas, presentes en las superficies de otros cuerpos sustentadores, similares a las que se encuentran en flujos transónicos. En regímenes de flujo supersónico, la resistencia de onda se divide comúnmente en dos componentes, resistencia de onda dependiente de la sustentación supersónica y resistencia de onda dependiente del volumen supersónico .

La solución de forma cerrada para la mínima resistencia de onda de un cuerpo de revolución con una longitud fija fue encontrada por Sears y Haack, y se conoce como la distribución de Sears-Haack . De manera similar, para un volumen fijo, la forma para la mínima resistencia de onda es la ojiva de Von Karman .

El concepto teórico del biplano Busemann no está sujeto a la resistencia de las olas cuando opera a su velocidad de diseño, pero es incapaz de generar sustentación en estas condiciones.

En 1752, D'Alembert demostró que el flujo potencial , la teoría de flujo no viscoso de última generación del siglo XVIII que se prestaba a soluciones matemáticas, daba como resultado la predicción de una resistencia cero. Esto estaba en contradicción con la evidencia experimental y se conoció como la paradoja de D'Alembert. En el siglo XIX, Saint-Venant , Navier y Stokes desarrollaron las ecuaciones de Navier-Stokes para la descripción del flujo viscoso . Stokes derivó la resistencia alrededor de una esfera a números de Reynolds muy bajos , cuyo resultado se llama ley de Stokes . ^[30]

En el límite de los números de Reynolds altos, las ecuaciones de Navier-Stokes se aproximan a las ecuaciones de Euler no viscosas , de las cuales las soluciones de flujo potencial consideradas por d'Alembert son soluciones. Sin embargo, todos los experimentos con números de Reynolds altos mostraron que existe resistencia. Los intentos de construir soluciones de flujo estable no viscoso para las ecuaciones de Euler, distintas de las soluciones de flujo potencial, no dieron resultados realistas. ^[30]

El concepto de capas límite —introducido por Prandtl en 1904, basado tanto en teoría como en experimentos— explicaba las causas de la fricción en los números de Reynolds altos. La capa límite es la capa delgada de fluido cercana al límite del objeto, donde los efectos viscosos siguen siendo importantes incluso cuando la viscosidad es muy pequeña (o equivalentemente, el número de Reynolds es muy grande). ^[30]

• 'Modelo empírico mejorado para la predicción de la resistencia de base en configuraciones de misiles, basado en nuevos datos del túnel de viento', Frank G Moore et al. Centro Langley de la NASA
• 'Investigación computacional de la reducción de la resistencia de base para un proyectil en diferentes regímenes de vuelo', MA Suliman et al. Actas de la 13.ª Conferencia internacional sobre ciencias aeroespaciales y tecnología de la aviación, ASAT-13, 26 al 28 de mayo de 2009
• 'Arrastre de base y bordes de salida gruesos', Sighard F. Hoerner, Air Materiel Command, en: Journal of the Aeronautical Sciences, octubre de 1950, págs. 622-628

• French, AP (1970). Mecánica newtoniana (Serie introductoria de física del MIT) (1.ª ed.). WW White & Company Inc., Nueva York. ISBN 978-0-393-09958-4.
• G. Falkovich (2011). Mecánica de fluidos (Un curso breve para físicos). Cambridge University Press. ISBN 978-1-107-00575-4.
• Serway, Raymond A.; Jewett, John W. (2004). Física para científicos e ingenieros (6.ª ed.). Brooks/Cole. ISBN 978-0-534-40842-8.
• Tipler, Paul (2004). Física para científicos e ingenieros: mecánica, oscilaciones y ondas, termodinámica (5.ª ed.). WH Freeman. ISBN 978-0-7167-0809-4.
• Huntley, HE (1967). Análisis dimensional . LOC 67-17978.
• Batchelor, George (2000). Introducción a la dinámica de fluidos . Cambridge Mathematical Library (2.ª ed.). Cambridge University Press . ISBN 978-0-521-66396-0.Señor 1744638  .
• L. J. Clancy (1975), Aerodinámica , Pitman Publishing Limited, Londres. ISBN 978-0-273-01120-0 
• Anderson, John D. Jr. (2000); Introducción al vuelo , Cuarta edición, McGraw Hill Higher Education, Boston, Massachusetts, EE. UU., 8.ª ed. 2015, ISBN 978-0078027673 . 

• Materiales educativos sobre la resistencia del aire.
• Resistencia aerodinámica y su efecto sobre la aceleración y la velocidad máxima de un vehículo.
• Calculadora de resistencia aerodinámica del vehículo basada en el coeficiente de resistencia, el área frontal y la velocidad.
• Sitio web How Things Fly del Museo Nacional del Aire y del Espacio del Instituto Smithsoniano
• Efecto de los hoyuelos en una pelota de golf y un coche