Teoría de la representación

La teoría de la representación es una rama de las matemáticas que estudia las estructuras algebraicas abstractas al representar sus elementos como transformaciones lineales de espacios vectoriales y estudia los módulos sobre estas estructuras algebraicas abstractas. ^{[1] [2]} En esencia, una representación hace que un objeto algebraico abstracto sea más concreto al describir sus elementos mediante matrices y sus operaciones algebraicas (por ejemplo, suma de matrices , multiplicación de matrices ). La teoría de matrices y operadores lineales es bien entendida, ^[3] por lo que las representaciones de objetos más abstractos en términos de objetos familiares del álgebra lineal ayudan a obtener propiedades y, a veces, simplifican los cálculos sobre teorías más abstractas.

Los objetos algebraicos que se pueden describir de esta manera incluyen grupos , álgebras asociativas y álgebras de Lie . La más destacada de ellas (e históricamente la primera) es la teoría de la representación de grupos , en la que los elementos de un grupo se representan mediante matrices invertibles de modo que la operación de grupo es la multiplicación de matrices. ^{[4] [5]}

La teoría de la representación es un método útil porque reduce los problemas del álgebra abstracta a problemas de álgebra lineal , un tema que se entiende bien. ^{[6] Por ejemplo, representar un grupo mediante un} espacio de Hilbert de dimensión infinita permite aplicar métodos de análisis a la teoría de grupos. ^{[7] [8]} Además, la teoría de la representación es importante en física porque puede describir cómo el grupo de simetría de un sistema físico afecta las soluciones de las ecuaciones que describen ese sistema. ^[9]

La teoría de la representación está muy extendida en todos los campos de las matemáticas. Las aplicaciones de la teoría de la representación son diversas. ^[10] Además de su impacto en el álgebra, la teoría de la representación

• generaliza el análisis de Fourier a través del análisis armónico , ^[11]
• está conectado a la geometría a través de la teoría invariante y el programa de Erlangen , ^[12]
• tiene un impacto en la teoría de números a través de formas automórficas y el programa Langlands . ^[13]

Existen diversos enfoques para la teoría de la representación. Los mismos objetos pueden estudiarse utilizando métodos de la geometría algebraica , la teoría de módulos , la teoría analítica de números , la geometría diferencial , la teoría de operadores , la combinatoria algebraica y la topología . ^[14]

El éxito de la teoría de la representación ha dado lugar a numerosas generalizaciones. Una de las más generales se encuentra en la teoría de categorías . ^[15] Los objetos algebraicos a los que se aplica la teoría de la representación pueden considerarse como tipos particulares de categorías, y las representaciones como funtores desde la categoría de objetos hasta la categoría de espacios vectoriales . ^[5] Esta descripción apunta a dos generalizaciones obvias: en primer lugar, los objetos algebraicos pueden reemplazarse por categorías más generales; en segundo lugar, la categoría objetivo de espacios vectoriales puede reemplazarse por otras categorías bien entendidas.

Sea un espacio vectorial sobre un cuerpo . ^[6] Por ejemplo, supongamos que es o , el espacio n -dimensional estándar de vectores columna sobre los números reales o complejos , respectivamente. En este caso, la idea de la teoría de la representación es hacer álgebra abstracta concretamente utilizando matrices de números reales o complejos.${\displaystyle V}$ ${\displaystyle \mathbb {F} }$${\displaystyle V}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \mathbb {C} ^{n}}$${\displaystyle n\times n}$

Hay tres tipos principales de objetos algebraicos para los que esto se puede hacer: grupos , álgebras asociativas y álgebras de Lie . ^{[16] [5]}

• El conjunto de todas las matrices invertibles es un grupo bajo la multiplicación de matrices , y la teoría de representación de grupos analiza un grupo describiendo ("representando") sus elementos en términos de matrices invertibles.${\displaystyle n\times n}$
• La suma y multiplicación de matrices forman el conjunto de todas las matrices en un álgebra asociativa y, por lo tanto, existe una teoría de representación correspondiente de las álgebras asociativas .${\displaystyle n\times n}$
• Si reemplazamos la multiplicación de matrices por el conmutador matricial , entonces las matrices se convierten en un álgebra de Lie, lo que conduce a una teoría de representación de álgebras de Lie .${\displaystyle MN}$ ${\displaystyle MN-NM}$${\displaystyle n\times n}$

Esto se generaliza a cualquier campo y cualquier espacio vectorial sobre , con aplicaciones lineales reemplazando matrices y composición reemplazando multiplicación de matrices: hay un grupo de automorfismos de , un álgebra asociativa de todos los endomorfismos de , y un álgebra de Lie correspondiente .${\displaystyle \mathbb {F} }$${\displaystyle V}$${\displaystyle \mathbb {F} }$ ${\displaystyle {\text{GL}}(V,\mathbb {F} )}$${\displaystyle V}$${\displaystyle {\text{End}}_{\mathbb {F} }(V)}$${\displaystyle V}$${\displaystyle {\mathfrak {gl}}(V,\mathbb {F} )}$

Hay dos formas de definir una representación. ^[17] La ​​primera utiliza la idea de una acción , generalizando la forma en que las matrices actúan sobre los vectores columna mediante la multiplicación de matrices.

Una representación de un grupo o álgebra (asociativa o de Lie) en un espacio vectorial es un mapa con dos propiedades. ${\displaystyle G}$${\displaystyle A}$${\displaystyle V}$$${\displaystyle \Phi \colon G\times V\to V\quad {\text{or}}\quad \Phi \colon A\times V\to V}$$

1. Para cualquier en (o en ), el mapa es lineal (sobre ). ${\displaystyle g}$${\displaystyle G}$${\displaystyle a}$${\displaystyle A}$$${\displaystyle {\begin{aligned}\Phi (g)\colon V&\to V\\v&\mapsto \Phi (g,v)\end{aligned}}}$$${\displaystyle \mathbb {F} }$
2. Si introducimos la notación g · v para ( g , v ), entonces para cualquier g ₁ , g ₂ en G y v en V : donde e es el elemento identidad de G y g ₁ g ₂ es el producto del grupo en G .${\displaystyle \Phi }$$${\displaystyle (2.1)\quad e\cdot v=v}$$$${\displaystyle (2.2)\quad g_{1}\cdot (g_{2}\cdot v)=(g_{1}g_{2})\cdot v}$$

La definición de álgebras asociativas es análoga, excepto que las álgebras asociativas no siempre tienen un elemento identidad, en cuyo caso se omite la ecuación (2.1). La ecuación (2.2) es una expresión abstracta de la asociatividad de la multiplicación de matrices. Esto no se cumple para el conmutador matricial y tampoco hay ningún elemento identidad para el conmutador. Por lo tanto, para las álgebras de Lie, el único requisito es que para cualquier x ₁ , x ₂ en A y v en V : donde [ x ₁ , x ₂ ] es el corchete de Lie , que generaliza el conmutador matricial MN − NM .$${\displaystyle (2.2')\quad x_{1}\cdot (x_{2}\cdot v)-x_{2}\cdot (x_{1}\cdot v)=[x_{1},x_{2}]\cdot v}$$

La segunda forma de definir una representación se centra en la función φ que envía g en G a una función lineal φ ( g ): V → V , que satisface

${\displaystyle \varphi (g_{1}g_{2})=\varphi (g_{1})\circ \varphi (g_{2})\quad {\text{for all }}g_{1},g_{2}\in G}$

Y lo mismo ocurre en los demás casos. Este enfoque es a la vez más conciso y más abstracto. Desde este punto de vista:

• una representación de un grupo G en un espacio vectorial V es un homomorfismo de grupo φ : G → GL( V , F ); ^[8]
• una representación de un álgebra asociativa A en un espacio vectorial V es un homomorfismo de álgebra φ : A → End _F ( V ); ^[8]
• una representación de un álgebra de Lie en un espacio vectorial es un homomorfismo de álgebra de Lie .${\displaystyle {\mathfrak {a}}}$${\displaystyle V}$ ${\displaystyle \phi :{\mathfrak {a}}\to {\mathfrak {gl}}(V,\mathbb {F} )}$

El espacio vectorial V se denomina espacio de representación de φ y su dimensión (si es finita) se denomina dimensión de la representación (a veces grado , como en ^[18] ). También es una práctica común referirse a V en sí mismo como la representación cuando el homomorfismo φ resulta claro a partir del contexto; de lo contrario, se puede utilizar la notación ( V , φ ) para denotar una representación.

Cuando V es de dimensión finita n , se puede elegir una base para V para identificar V con F ⁿ , y así recuperar una representación matricial con entradas en el campo F .

Una representación efectiva o fiel es una representación ( V , φ ), para la cual el homomorfismo φ es inyectivo .

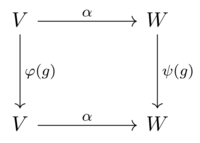
Si V y W son espacios vectoriales sobre F , equipados con representaciones φ y ψ de un grupo G , entonces una función equivariante de V a W es una función lineal α : V → W tal que

${\displaystyle \alpha (g\cdot v)=g\cdot \alpha (v)}$

para todo g en G y v en V . En términos de φ : G → GL( V ) y ψ : G → GL( W ), esto significa

${\displaystyle \alpha \circ \varphi (g)=\psi (g)\circ \alpha }$

para todo g en G , es decir, el siguiente diagrama conmuta :

Los mapas equivariantes para representaciones de un álgebra asociativa o de Lie se definen de manera similar. Si α es invertible, entonces se dice que es un isomorfismo , en cuyo caso V y W (o, más precisamente, φ y ψ ) son representaciones isomorfas , también denominadas representaciones equivalentes . Un mapa equivariante a menudo se denomina mapa entrelazado de representaciones. Además, en el caso de un grupo G , en ocasiones se lo denomina G -mapa.

Las representaciones isomorfas son, a efectos prácticos, "lo mismo"; proporcionan la misma información sobre el grupo o álgebra que se representa. Por lo tanto, la teoría de la representación busca clasificar las representaciones hasta el isomorfismo .

Si es una representación de (por ejemplo) un grupo , y es un subespacio lineal de que se conserva por la acción de en el sentido de que para todos y , ( Serre los llama estables en ^[18] ), entonces se llama una subrepresentación : al definir donde es la restricción de a , es una representación de y la inclusión de es una función equivariante. El espacio cociente también se puede convertir en una representación de . Si tiene exactamente dos subrepresentaciones, a saber, el subespacio trivial {0} y él mismo, entonces se dice que la representación es irreducible ; si tiene una subrepresentación no trivial propia, se dice que la representación es reducible . ^[19]${\displaystyle (V,\psi )}$${\displaystyle G}$${\displaystyle W}$${\displaystyle V}$${\displaystyle G}$${\displaystyle w\in W}$${\displaystyle g\in G}$${\displaystyle g\cdot w\in W}$${\displaystyle W}$ ${\displaystyle G}$${\displaystyle W}$$${\displaystyle \phi :G\to {\text{Aut}}(W)}$$${\displaystyle \phi (g)}$${\displaystyle \psi (g)}$${\displaystyle W}$${\displaystyle (W,\phi )}$${\displaystyle G}$${\displaystyle W\hookrightarrow V}$ ${\displaystyle V/W}$${\displaystyle G}$${\displaystyle V}$${\displaystyle V}$${\displaystyle V}$

La definición de una representación irreducible implica el lema de Schur : una función equivariante entre representaciones irreducibles es la función cero o un isomorfismo, ya que su núcleo e imagen son subrepresentaciones. En particular, cuando , esto muestra que los endomorfismos equivariantes de forman un álgebra de división asociativa sobre el cuerpo subyacente F . Si F es algebraicamente cerrado , los únicos endomorfismos equivariantes de una representación irreducible son los múltiplos escalares de la identidad.$${\displaystyle \alpha :(V,\psi )\to (V',\psi ')}$$${\displaystyle V=V'}$${\displaystyle V}$

Las representaciones irreducibles son los bloques de construcción de la teoría de la representación para muchos grupos: si una representación no es irreducible, entonces se construye a partir de una subrepresentación y un cociente que son ambos "más simples" en algún sentido; por ejemplo, si es de dimensión finita, entonces tanto la subrepresentación como el cociente tienen una dimensión menor. Hay contraejemplos donde una representación tiene una subrepresentación, pero solo tiene un componente irreducible no trivial. Por ejemplo, el grupo aditivo tiene una representación bidimensional Este grupo tiene el vector fijado por este homomorfismo, pero el subespacio complementario se asigna a dando solo una subrepresentación irreducible. Esto es cierto para todos los grupos unipotentes . ^{[20] : 112}${\displaystyle V}$${\displaystyle V}$${\displaystyle (\mathbb {R} ,+)}$$${\displaystyle \phi (a)={\begin{bmatrix}1&a\\0&1\end{bmatrix}}}$$${\displaystyle {\begin{bmatrix}1&0\end{bmatrix}}^{\mathsf {T}}}$$${\displaystyle {\begin{bmatrix}0\\1\end{bmatrix}}\mapsto {\begin{bmatrix}a\\1\end{bmatrix}}}$$

Si ( V , φ ) y ( W , ψ ) son representaciones de (digamos) un grupo G , entonces la suma directa de V y W es una representación, de manera canónica, a través de la ecuación

${\displaystyle g\cdot (v,w)=(g\cdot v,g\cdot w).}$

La suma directa de dos representaciones no aporta más información sobre el grupo G que las dos representaciones individualmente. Si una representación es la suma directa de dos subrepresentaciones propias no triviales, se dice que es descomponible. En caso contrario, se dice que es indescomponible.

En circunstancias favorables, toda representación de dimensión finita es una suma directa de representaciones irreducibles: se dice que dichas representaciones son semisimples . En este caso, basta con entender sólo las representaciones irreducibles. Entre los ejemplos en los que se produce este fenómeno de " reducibilidad completa " se incluyen los grupos finitos (véase el teorema de Maschke ), los grupos compactos y las álgebras de Lie semisimples.

En los casos en que la reducibilidad completa no se cumple, hay que entender cómo se pueden construir representaciones indecomponibles a partir de representaciones irreducibles como extensiones de un cociente por una subrepresentación.

Supongamos que y son representaciones de un grupo . Entonces podemos formar una representación de G actuando sobre el espacio vectorial del producto tensorial de la siguiente manera: ^[21]${\displaystyle \phi _{1}:G\rightarrow \mathrm {GL} (V_{1})}$${\displaystyle \phi _{2}:G\rightarrow \mathrm {GL} (V_{2})}$${\displaystyle G}$${\displaystyle \phi _{1}\otimes \phi _{2}}$${\displaystyle V_{1}\otimes V_{2}}$

${\displaystyle (\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)}$.

Si y son representaciones de un álgebra de Lie, entonces la fórmula correcta a utilizar es ^[22]${\displaystyle \phi _{1}}$${\displaystyle \phi _{2}}$

${\displaystyle (\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)}$.

Este producto puede reconocerse como el coproducto de una coalgebra . En general, el producto tensorial de representaciones irreducibles no es irreducible; el proceso de descomposición de un producto tensorial como una suma directa de representaciones irreducibles se conoce como teoría de Clebsch-Gordan .

En el caso de la teoría de representación del grupo SU(2) (o equivalentemente, de su álgebra de Lie complejizada ), la descomposición es fácil de resolver. ^[23] Las representaciones irreducibles están etiquetadas por un parámetro que es un entero no negativo o medio entero; la representación entonces tiene dimensión . Supongamos que tomamos el producto tensorial de la representación de dos representaciones, con etiquetas y donde asumimos . Entonces el producto tensorial se descompone como una suma directa de una copia de cada representación con etiqueta , donde varía de a en incrementos de 1. Si, por ejemplo, , entonces los valores de que ocurren son 0, 1 y 2. Por lo tanto, la representación del producto tensorial de dimensión se descompone como una suma directa de una representación unidimensional , una representación tridimensional y una representación pentadimensional .${\displaystyle \mathrm {sl} (2;\mathbb {C} )}$${\displaystyle l}$${\displaystyle 2l+1}$${\displaystyle l_{1}}$${\displaystyle l_{2},}$${\displaystyle l_{1}\geq l_{2}}$${\displaystyle l}$${\displaystyle l}$${\displaystyle l_{1}-l_{2}}$${\displaystyle l_{1}+l_{2}}$${\displaystyle l_{1}=l_{2}=1}$${\displaystyle l}$${\displaystyle (2l_{1}+1)\times (2l_{2}+1)=3\times 3=9}$${\displaystyle (l=0),}$${\displaystyle (l=1),}$${\displaystyle (l=2)}$

La teoría de la representación se distingue por la cantidad de ramas que tiene y por la diversidad de enfoques para estudiar las representaciones de grupos y álgebras. Si bien todas las teorías tienen en común los conceptos básicos que ya hemos analizado, difieren considerablemente en los detalles. Las diferencias son al menos tres:

1. La teoría de la representación depende del tipo de objeto algebraico que se representa. Existen varias clases diferentes de grupos, álgebras asociativas y álgebras de Lie, y sus teorías de representación tienen cada una un matiz individual.
2. La teoría de la representación depende de la naturaleza del espacio vectorial en el que se representa el objeto algebraico. La distinción más importante es entre representaciones de dimensión finita y de dimensión infinita. En el caso de dimensión infinita, son importantes las estructuras adicionales (por ejemplo, si el espacio es o no un espacio de Hilbert , un espacio de Banach , etc.). También se pueden imponer estructuras algebraicas adicionales en el caso de dimensión finita.
3. La teoría de la representación depende del tipo de campo sobre el que se define el espacio vectorial. Los casos más importantes son el campo de los números complejos, el campo de los números reales, los campos finitos y los campos de números p-ádicos . Surgen dificultades adicionales para los campos de característica positiva y para los campos que no son algebraicamente cerrados .

Las representaciones de grupos son una herramienta muy importante en el estudio de grupos finitos. ^[24] También surgen en las aplicaciones de la teoría de grupos finitos a la geometría y la cristalografía . ^[25] Las representaciones de grupos finitos exhiben muchas de las características de la teoría general y señalan el camino a otras ramas y temas en la teoría de la representación.

Sobre un cuerpo de característica cero , la representación de un grupo finito G tiene varias propiedades convenientes. En primer lugar, las representaciones de G son semisimples (completamente reducibles). Esto es una consecuencia del teorema de Maschke , que establece que cualquier subrepresentación V de una G -representación W tiene un complemento G -invariante. Una prueba es elegir cualquier proyección π de W a V y reemplazarla por su media π _G definida por

${\displaystyle \pi _{G}(x)={\frac {1}{|G|}}\sum _{g\in G}g\cdot \pi (g^{-1}\cdot x).}$

π _G es equivariante y su núcleo es el complemento requerido.

Las representaciones G de dimensión finita se pueden entender utilizando la teoría de caracteres : el carácter de una representación φ : G → GL( V ) es la función de clase χ _φ : G → F definida por

${\displaystyle \chi _{\varphi }(g)=\mathrm {Tr} (\varphi (g))}$

donde está la traza . Una representación irreducible de G está completamente determinada por su carácter.${\displaystyle \mathrm {Tr} }$

El teorema de Maschke se cumple de manera más general para cuerpos de característica positiva p , como los cuerpos finitos , siempre que el primo p sea coprimo con respecto al orden de G . Cuando p y | G | tienen un factor común , existen G -representaciones que no son semisimples, que se estudian en una subrama llamada teoría de representaciones modulares .

Las técnicas de promediado también muestran que si F son números reales o complejos, entonces cualquier representación G conserva un producto interno en V en el sentido de que${\displaystyle \langle \cdot ,\cdot \rangle }$

${\displaystyle \langle g\cdot v,g\cdot w\rangle =\langle v,w\rangle }$

para todo g en G y v , w en W . Por lo tanto, cualquier representación de G es unitaria .

Las representaciones unitarias son automáticamente semisimples, ya que el resultado de Maschke puede demostrarse tomando el complemento ortogonal de una subrepresentación. Al estudiar representaciones de grupos que no son finitos, las representaciones unitarias proporcionan una buena generalización de las representaciones reales y complejas de un grupo finito.

Resultados como el teorema de Maschke y la propiedad unitaria que se basan en el promedio se pueden generalizar a grupos más generales reemplazando el promedio por una integral, siempre que se pueda definir una noción adecuada de integral. Esto se puede hacer para grupos topológicos compactos (incluidos los grupos de Lie compactos), utilizando la medida de Haar , y la teoría resultante se conoce como análisis armónico abstracto .

Sobre cuerpos arbitrarios, otra clase de grupos finitos que tienen una buena teoría de representación son los grupos finitos de tipo Lie . Ejemplos importantes son los grupos algebraicos lineales sobre cuerpos finitos. La teoría de representación de los grupos algebraicos lineales y los grupos de Lie extiende estos ejemplos a los grupos de dimensión infinita, estando estos últimos íntimamente relacionados con las representaciones del álgebra de Lie . La importancia de la teoría de caracteres para los grupos finitos tiene un análogo en la teoría de pesos para las representaciones de los grupos de Lie y las álgebras de Lie.

Las representaciones de un grupo finito G también están vinculadas directamente a las representaciones algebraicas a través del álgebra de grupo F [ G ], que es un espacio vectorial sobre F con los elementos de G como base, equipado con la operación de multiplicación definida por la operación de grupo, linealidad y el requisito de que la operación de grupo y la multiplicación escalar conmuten.

Las representaciones modulares de un grupo finito G son representaciones sobre un cuerpo cuya característica no es coprima con | G |, de modo que el teorema de Maschke ya no se cumple (porque | G | no es invertible en F y por lo tanto no se puede dividir por él). ^[26] Sin embargo, Richard Brauer extendió gran parte de la teoría de caracteres a representaciones modulares, y esta teoría jugó un papel importante en el progreso temprano hacia la clasificación de grupos simples finitos , especialmente para grupos simples cuya caracterización no era susceptible de métodos puramente teóricos de grupos porque sus 2-subgrupos de Sylow eran "demasiado pequeños". ^[27]

Además de tener aplicaciones en la teoría de grupos, las representaciones modulares surgen naturalmente en otras ramas de las matemáticas , como la geometría algebraica , la teoría de codificación , la combinatoria y la teoría de números .

Una representación unitaria de un grupo G es una representación lineal φ de G en un espacio de Hilbert real o (usualmente) complejo V tal que φ ( g ) es un operador unitario para cada g ∈ G . Tales representaciones han sido ampliamente aplicadas en mecánica cuántica desde la década de 1920, gracias en particular a la influencia de Hermann Weyl , ^[28] y esto ha inspirado el desarrollo de la teoría, más notablemente a través del análisis de representaciones del grupo de Poincaré por Eugene Wigner . ^[29] Uno de los pioneros en construir una teoría general de representaciones unitarias (para cualquier grupo G en lugar de solo para grupos particulares útiles en aplicaciones) fue George Mackey , y una teoría extensa fue desarrollada por Harish-Chandra y otros en las décadas de 1950 y 1960. ^[30]

Un objetivo principal es describir el " dual unitario " , el espacio de representaciones unitarias irreducibles de G. ^[31] La teoría está mejor desarrollada en el caso de que G sea un grupo topológico localmente compacto (Hausdorff) y las representaciones sean fuertemente continuas . ^[11] Para G abeliano, el dual unitario es solo el espacio de caracteres , mientras que para G compacto, el teorema de Peter-Weyl muestra que las representaciones unitarias irreducibles son de dimensión finita y el dual unitario es discreto. ^[32] Por ejemplo, si G es el grupo circular S ¹ , entonces los caracteres se dan por números enteros y el dual unitario es Z .

Para G no compacto , la cuestión de qué representaciones son unitarias es sutil. Aunque las representaciones unitarias irreducibles deben ser "admisibles" (como los módulos de Harish-Chandra ) y es fácil detectar qué representaciones admisibles tienen una forma sesquilineal invariante no degenerada , es difícil determinar cuándo esta forma es definida positiva. Una descripción eficaz del dual unitario, incluso para grupos relativamente bien comportados como los grupos de Lie reductivos reales (discutidos más adelante), sigue siendo un importante problema abierto en la teoría de la representación. Se ha resuelto para muchos grupos particulares, como SL(2, R ) y el grupo de Lorentz . ^[33]

La dualidad entre el grupo de círculos S ¹ y los números enteros Z , o más generalmente, entre un toro T ⁿ y Z ⁿ es bien conocida en análisis como la teoría de las series de Fourier , y la transformada de Fourier expresa de manera similar el hecho de que el espacio de caracteres en un espacio vectorial real es el espacio vectorial dual . Por lo tanto, la teoría de la representación unitaria y el análisis armónico están íntimamente relacionados, y el análisis armónico abstracto explota esta relación, desarrollando el análisis de funciones en grupos topológicos localmente compactos y espacios relacionados. ^[11]

Un objetivo principal es proporcionar una forma general de la transformada de Fourier y el teorema de Plancherel . Esto se hace construyendo una medida en el dual unitario y un isomorfismo entre la representación regular de G en el espacio L ² ( G ) de funciones integrables cuadradas en G y su representación en el espacio de L ² funciones en el dual unitario. La dualidad de Pontrjagin y el teorema de Peter-Weyl logran esto para G abeliano y compacto respectivamente. ^{[32] [34]}

Otro enfoque implica considerar todas las representaciones unitarias, no solo las irreducibles. Estas forman una categoría , y la dualidad de Tannaka-Krein proporciona una manera de recuperar un grupo compacto a partir de su categoría de representaciones unitarias.

Si el grupo no es ni abeliano ni compacto, no se conoce ninguna teoría general con un análogo del teorema de Plancherel o la inversión de Fourier, aunque Alexander Grothendieck extendió la dualidad de Tannaka-Krein a una relación entre grupos algebraicos lineales y categorías tannakianas .

El análisis armónico también se ha extendido desde el análisis de funciones en un grupo G a funciones en espacios homogéneos para G. La teoría está particularmente bien desarrollada para espacios simétricos y proporciona una teoría de formas automórficas (que se analizan a continuación).

Lie groups and Lie algebras
Classical groups General linear GL(n) Special linear SL(n) Orthogonal O(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n)
Simple Lie groups Classical An Bn Cn Dn Exceptional G2 F4 E6 E7 E8
Other Lie groups Circle Lorentz Poincaré Conformal group Diffeomorphism Loop Euclidean
Lie algebras Lie group–Lie algebra correspondence Exponential map Adjoint representation Killing form Index Simple Lie algebra Loop algebra Affine Lie algebra
Semisimple Lie algebra Dynkin diagrams Cartan subalgebra Root system Weyl group Real form Complexification Split Lie algebra Compact Lie algebra
Representation theory Lie group representation Lie algebra representation Representation theory of semisimple Lie algebras Representations of classical Lie groups Theorem of the highest weight Borel–Weil–Bott theorem
Lie groups in physics Particle physics and representation theory Lorentz group representations Poincaré group representations Galilean group representations
Scientists Sophus Lie Henri Poincaré Wilhelm Killing Élie Cartan Hermann Weyl Claude Chevalley Harish-Chandra Armand Borel
Glossary Table of Lie groups
v t e

Un grupo de Lie es un grupo que también es una variedad suave . Muchos grupos clásicos de matrices sobre números reales o complejos son grupos de Lie. ^[35] Muchos de los grupos importantes en física y química son grupos de Lie, y su teoría de representación es crucial para la aplicación de la teoría de grupos en esos campos. ^[9]

La teoría de representación de los grupos de Lie se puede desarrollar primero considerando los grupos compactos, a los que se aplican los resultados de la teoría de representación compacta. ^[31] Esta teoría se puede extender a representaciones de dimensión finita de grupos de Lie semisimples utilizando el truco unitario de Weyl : cada grupo de Lie real semisimple G tiene una complejización, que es un grupo de Lie complejo G ^c , y este grupo de Lie complejo tiene un subgrupo compacto maximal K . Las representaciones de dimensión finita de G corresponden estrechamente a las de K .

Un grupo de Lie general es un producto semidirecto de un grupo de Lie resoluble y un grupo de Lie semisimple (la descomposición de Levi ). ^[36] La clasificación de representaciones de grupos de Lie resolubles es intratable en general, pero a menudo fácil en casos prácticos. Las representaciones de productos semidirectos pueden analizarse por medio de resultados generales llamados teoría de Mackey , que es una generalización de los métodos utilizados en la clasificación de Wigner de representaciones del grupo de Poincaré.

Un álgebra de Lie sobre un cuerpo F es un espacio vectorial sobre F equipado con una operación bilineal antisimétrica llamada corchete de Lie , que satisface la identidad de Jacobi . Las álgebras de Lie surgen en particular como espacios tangentes a los grupos de Lie en el elemento identidad , lo que lleva a su interpretación como "simetrías infinitesimales". ^[36] Un enfoque importante para la teoría de la representación de los grupos de Lie es estudiar la teoría de la representación correspondiente de las álgebras de Lie, pero las representaciones de las álgebras de Lie también tienen un interés intrínseco. ^[37]

Las álgebras de Lie, al igual que los grupos de Lie, tienen una descomposición de Levi en partes semisimples y resolubles, siendo la teoría de la representación de las álgebras de Lie resolubles intratable en general. Por el contrario, las representaciones de dimensión finita de las álgebras de Lie semisimples se entienden completamente, después del trabajo de Élie Cartan . Una representación de un álgebra de Lie semisimple 𝖌 se analiza eligiendo una subálgebra de Cartan , que es esencialmente una subálgebra máxima genérica 𝖍 de 𝖌 en la que el corchete de Lie es cero ("abeliana"). La representación de 𝖌 se puede descomponer en espacios de peso que son espacios propios para la acción de 𝖍 y el análogo infinitesimal de los caracteres. La estructura de las álgebras de Lie semisimples reduce entonces el análisis de las representaciones a una combinatoria de fácil comprensión de los posibles pesos que pueden ocurrir. ^[36]

Existen muchas clases de álgebras de Lie de dimensión infinita cuyas representaciones han sido estudiadas. Entre ellas, una clase importante son las álgebras de Kac-Moody. ^[38] Reciben su nombre en honor a Victor Kac y Robert Moody , quienes las descubrieron de forma independiente. Estas álgebras forman una generalización de las álgebras de Lie semisimples de dimensión finita y comparten muchas de sus propiedades combinatorias. Esto significa que tienen una clase de representaciones que pueden entenderse de la misma manera que las representaciones de las álgebras de Lie semisimples.

Las álgebras de Lie afines son un caso especial de las álgebras de Kac-Moody, que tienen particular importancia en matemáticas y física teórica , especialmente la teoría de campos conformes y la teoría de modelos exactamente resolubles . Kac descubrió una elegante demostración de ciertas identidades combinatorias, las identidades de Macdonald , que se basa en la teoría de representación de las álgebras de Kac-Moody afines.

Las superálgebras de Lie son generalizaciones de las álgebras de Lie en las que el espacio vectorial subyacente tiene una gradación Z ₂ y las propiedades de simetría antisimétrica e identidad de Jacobi del corchete de Lie se modifican mediante signos. Su teoría de representación es similar a la teoría de representación de las álgebras de Lie. ^[39]

Los grupos algebraicos lineales (o más generalmente, esquemas de grupos afines ) son análogos en geometría algebraica de los grupos de Lie , pero sobre cuerpos más generales que solo R o C. En particular, sobre cuerpos finitos, dan lugar a grupos finitos de tipo Lie . Aunque los grupos algebraicos lineales tienen una clasificación que es muy similar a la de los grupos de Lie, su teoría de representación es bastante diferente (y mucho menos entendida) y requiere técnicas diferentes, ya que la topología de Zariski es relativamente débil y las técnicas de análisis ya no están disponibles. ^[40]

La teoría de invariantes estudia las acciones sobre las variedades algebraicas desde el punto de vista de su efecto sobre las funciones, que forman representaciones del grupo. Clásicamente, la teoría se ocupaba de la cuestión de la descripción explícita de funciones polinómicas que no cambian, o son invariantes , bajo las transformaciones de un grupo lineal dado . El enfoque moderno analiza la descomposición de estas representaciones en irreducibles. ^[41]

La teoría invariante de grupos infinitos está inextricablemente vinculada con el desarrollo del álgebra lineal , especialmente, las teorías de formas cuadráticas y determinantes . Otro tema con fuerte influencia mutua es la geometría proyectiva , donde la teoría invariante puede usarse para organizar el tema, y ​​durante la década de 1960, David Mumford le dio nueva vida al tema en forma de su teoría invariante geométrica . ^[42]

La teoría de la representación de los grupos de Lie semisimples tiene sus raíces en la teoría de invariantes ^[35] y los fuertes vínculos entre la teoría de la representación y la geometría algebraica tienen muchos paralelos en la geometría diferencial, comenzando con el programa de Erlangen de Felix Klein y las conexiones de Élie Cartan , que colocan a los grupos y la simetría en el corazón de la geometría. ^[43] Los desarrollos modernos vinculan la teoría de la representación y la teoría de invariantes a áreas tan diversas como la holonomía , los operadores diferenciales y la teoría de varias variables complejas .

Las formas automórficas son una generalización de las formas modulares a funciones analíticas más generales , quizás de varias variables complejas , con propiedades de transformación similares. ^[44] La generalización implica reemplazar el grupo modular PSL ₂ ( R ) y un subgrupo de congruencia elegido por un grupo de Lie semisimple G y un subgrupo discreto Γ . Así como las formas modulares pueden verse como formas diferenciales en un cociente del espacio de la mitad superior H = PSL ₂ ( R )/SO(2), las formas automórficas pueden verse como formas diferenciales (u objetos similares) en Γ \ G / K , donde K es (típicamente) un subgrupo compacto maximal de G . Sin embargo, se requiere cierto cuidado, ya que el cociente típicamente tiene singularidades. El cociente de un grupo de Lie semisimple por un subgrupo compacto es un espacio simétrico y, por lo tanto, la teoría de las formas automórficas está íntimamente relacionada con el análisis armónico en espacios simétricos.

Antes del desarrollo de la teoría general, se habían estudiado en detalle muchos casos especiales importantes, incluidas las formas modulares de Hilbert y las formas modulares de Siegel . Entre los resultados importantes de la teoría se incluyen la fórmula de la traza de Selberg y la constatación por parte de Robert Langlands de que el teorema de Riemann-Roch podía aplicarse para calcular la dimensión del espacio de las formas automórficas. La noción posterior de "representación automórfica" ha demostrado tener un gran valor técnico para tratar el caso en el que G es un grupo algebraico , tratado como un grupo algebraico adélico . Como resultado, se ha desarrollado toda una filosofía, el programa Langlands , en torno a la relación entre la representación y las propiedades teóricas de los números de las formas automórficas. ^[45]

En cierto sentido, las representaciones del álgebra asociativa generalizan tanto las representaciones de grupos como las álgebras de Lie. Una representación de un grupo induce una representación de un anillo de grupo o álgebra de grupo correspondiente , mientras que las representaciones de un álgebra de Lie corresponden biyectivamente a representaciones de su álgebra envolvente universal . Sin embargo, la teoría de la representación de las álgebras asociativas generales no tiene todas las buenas propiedades de la teoría de la representación de grupos y las álgebras de Lie.

Al considerar las representaciones de un álgebra asociativa, se puede olvidar el cuerpo subyacente y considerar simplemente el álgebra asociativa como un anillo y sus representaciones como módulos. Este enfoque es sorprendentemente fructífero: muchos resultados en teoría de representaciones se pueden interpretar como casos especiales de resultados sobre módulos sobre un anillo.

Las álgebras de Hopf proporcionan una forma de mejorar la teoría de representación de las álgebras asociativas, al tiempo que conservan la teoría de representación de grupos y las álgebras de Lie como casos especiales. En particular, el producto tensorial de dos representaciones es una representación, al igual que el espacio vectorial dual.

Las álgebras de Hopf asociadas a grupos tienen una estructura de álgebra conmutativa, por lo que las álgebras de Hopf generales se conocen como grupos cuánticos , aunque este término suele restringirse a ciertas álgebras de Hopf que surgen como deformaciones de grupos o sus álgebras envolventes universales. La teoría de la representación de los grupos cuánticos ha añadido ideas sorprendentes a la teoría de la representación de los grupos de Lie y las álgebras de Lie, por ejemplo a través de la base cristalina de Kashiwara.

Una representación de teoría de conjuntos (también conocida como representación de acción de grupo o de permutación ) de un grupo G en un conjunto X está dada por una función ρ de G a X ^X , el conjunto de funciones de X a X , tales que para todos los g ₁ , g ₂ en G y todos los x en X :

${\displaystyle \rho (1)[x]=x}$

${\displaystyle \rho (g_{1}g_{2})[x]=\rho (g_{1})[\rho (g_{2})[x]].}$

Esta condición y los axiomas para un grupo implican que ρ ( g ) es una biyección (o permutación ) para todo g en G . Por lo tanto, podemos definir de manera equivalente una representación de permutación como un homomorfismo de grupo desde G hasta el grupo simétrico S _X de X .

Cada grupo G puede considerarse como una categoría con un único objeto; los morfismos en esta categoría son simplemente los elementos de G. Dada una categoría arbitraria C , una representación de G en C es un funtor de G a C. Tal funtor selecciona un objeto X en C y un homomorfismo de grupo de G a Aut( X ) , el grupo de automorfismos de X.

En el caso en que C sea Vect _F , la categoría de espacios vectoriales sobre un cuerpo F , esta definición es equivalente a una representación lineal. De la misma manera, una representación de teoría de conjuntos es simplemente una representación de G en la categoría de conjuntos .

Como otro ejemplo , considere la categoría de espacios topológicos Top . Las representaciones en Top son homomorfismos desde G hasta el grupo de homeomorfismos de un espacio topológico X.

Tres tipos de representaciones estrechamente relacionadas con las representaciones lineales son:

• Representaciones proyectivas : pertenecen a la categoría de espacios proyectivos . Se pueden describir como "representaciones lineales hasta transformaciones escalares".
• Representaciones afines : en la categoría de espacios afines . Por ejemplo, el grupo euclidiano actúa de manera afín sobre el espacio euclidiano .
• correpresentaciones de grupos unitarios y antiunitarios : en la categoría de espacios vectoriales complejos con morfismos que son transformaciones lineales o antilineales .

Dado que los grupos son categorías, también se puede considerar la representación de otras categorías. La generalización más simple es a los monoides , que son categorías con un objeto. Los grupos son monoides para los cuales cada morfismo es invertible. Los monoides generales tienen representaciones en cualquier categoría. En la categoría de conjuntos, estas son acciones de monoides , pero se pueden estudiar representaciones de monoides en espacios vectoriales y otros objetos.

En términos más generales, se puede relajar el supuesto de que la categoría representada tiene un solo objeto. En términos generales, se trata simplemente de la teoría de funtores entre categorías, y poco se puede decir al respecto.

Un caso especial ha tenido un impacto significativo en la teoría de la representación, a saber, la teoría de la representación de carcajs. ^[15] Un carcaj es simplemente un gráfico dirigido (con bucles y flechas múltiples permitidos), pero se puede convertir en una categoría (y también en un álgebra) considerando caminos en el gráfico. Las representaciones de tales categorías/álgebras han iluminado varios aspectos de la teoría de la representación, por ejemplo, al permitir que las preguntas de la teoría de la representación no semisimple sobre un grupo se reduzcan en algunos casos a preguntas de la teoría de la representación semisimple sobre un carcaj.

• Alperin, JL (1986), Teoría de la representación local: representaciones modulares como introducción a la teoría de la representación local de grupos finitos , Cambridge University Press, ISBN 978-0-521-44926-7.
• Bargmann, V. (1947), "Representaciones unitarias irreducibles del grupo de Lorenz", Annals of Mathematics , 48 ​​(3): 568–640, doi :10.2307/1969129, JSTOR  1969129.
• Borel, Armand (2001), Ensayos sobre la historia de los grupos de Lie y los grupos algebraicos , American Mathematical Society, ISBN 978-0-8218-0288-5.
• Borel, Armand; Casselman, W. (1979), Formas automórficas, representaciones y funciones L , American Mathematical Society, ISBN 978-0-8218-1435-2.
• Curtis, Charles W. ; Reiner, Irving (1962), Teoría de la representación de grupos finitos y álgebras asociativas , John Wiley & Sons (reedición 2006 por AMS Bookstore), ISBN 978-0-470-18975-7.
• Folland, Gerald B. (1995), Un curso de análisis armónico abstracto , CRC Press, ISBN 978-0-8493-8490-5.
• Fulton, William ; Harris, Joe (1991). Teoría de la representación. Un primer curso . Textos de posgrado en matemáticas , Lecturas en matemáticas. Vol. 129. Nueva York: Springer-Verlag. doi :10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. Sr.  1153249. OCLC  246650103..
• Gelbart, Stephen (1984), "Una introducción elemental al programa Langlands", Boletín de la Sociedad Matemática Americana , 10 (2): 177–219, doi : 10.1090/S0273-0979-1984-15237-6.
• Goodman, Roe; Wallach, Nolan R. (1998), Representaciones e invariantes de los grupos clásicos , Cambridge University Press, ISBN 978-0-521-66348-9.
• Hall, Brian C. (2015), Grupos de Lie, álgebras de Lie y representaciones: una introducción elemental , Textos de posgrado en matemáticas, vol. 222 (2.ª ed.), Springer, ISBN 978-3319134666
• Helgason, Sigurdur (1978), Geometría diferencial, grupos de Lie y espacios simétricos , Academic Press, ISBN 978-0-12-338460-7
• Humphreys, James E. (1972a), Introducción a las álgebras de Lie y la teoría de la representación , Birkhäuser, ISBN 978-0-387-90053-7.
• Humphreys, James E. (1972b), Grupos algebraicos lineales , Textos de posgrado en matemáticas, vol. 21, Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-90108-4, Sr.  0396773
• James, Gordon; Liebeck, Martin (1993), Representaciones y caracteres de grupos , Cambridge: Cambridge University Press, ISBN 978-0-521-44590-0.
• Jantzen, Jens Carsten (2003), Representaciones de grupos algebraicos , Sociedad Matemática Estadounidense, ISBN 978-0-8218-3527-2.
• Kac, Victor G. (1977), "Superálgebras de Lie", Advances in Mathematics , 26 (1): 8–96, doi : 10.1016/0001-8708(77)90017-2.
• Kac, Victor G. (1990), Álgebras de Lie de dimensión infinita (3.ª ed.), Cambridge University Press, ISBN 978-0-521-46693-6.
• Kim, Shoon Kyung (1999), Métodos teóricos de grupos y aplicaciones a moléculas y cristales: y aplicaciones a moléculas y cristales , Cambridge University Press, ISBN 978-0-521-64062-6.
• Knapp, Anthony W. (2001), Teoría de la representación de grupos semisimples: una descripción general basada en ejemplos , Princeton University Press, ISBN 978-0-691-09089-4.
• Kostrikin, AI ; Manin, Yuri I. (1997), Álgebra lineal y geometría , Taylor & Francis, ISBN 978-90-5699-049-7.
• Lam, TY (1998), "Representaciones de grupos finitos: cien años", Avisos de la AMS , 45 (3, 4): 361–372 (Parte I), 465–474 (Parte II).
• Lyubich, Yurii I. (1988). Introducción a la teoría de representaciones de grupos de Banach . Teoría de operadores: avances y aplicaciones. Vol. 30. Basilea: Birkhauser. ISBN 978-3-7643-2207-6.
• Mumford, David ; Fogarty, J.; Kirwan, F. (1994), Teoría invariante geométrica , Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Resultados en Matemáticas y Áreas Afines (2)], vol. 34 (3.ª ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-56963-3, Sr.  0214602; SEÑOR 0719371 (2ª ed.); SEÑOR 1304906 (3ª ed.)
• Olver, Peter J. (1999), Teoría invariante clásica , Cambridge: Cambridge University Press, ISBN 978-0-521-55821-1.
• Pedro, F.; Weyl, Hermann (1927), "Die Vollständigkeit der primitiven Darstellungen einer geschlossenen kontinuierlichen Gruppe", Mathematische Annalen , 97 (1): 737–755, doi :10.1007/BF01447892, S2CID  120013521.
• Pontrjagin, Lev S. (1934), "La teoría de los grupos conmutativos topológicos", Annals of Mathematics , 35 (2): 361–388, doi :10.2307/1968438, JSTOR  1968438.
• Sally, Paul ; Vogan, David A. (1989), Teoría de la representación y análisis armónico en grupos de Lie semisimples , American Mathematical Society, ISBN 978-0-8218-1526-7.
• Serre, Jean-Pierre (1977), Representaciones lineales de grupos finitos , Springer-Verlag, ISBN 978-0387901909.
• Sharpe, Richard W. (1997), Geometría diferencial: generalización de Cartan del programa de Erlangen de Klein , Springer, ISBN 978-0-387-94732-7.
• Simson, Daniel; Skowronski, Andrzej; Assem, Ibrahim (2007), Elementos de la teoría de representación de álgebras asociativas , Cambridge University Press, ISBN 978-0-521-88218-7.
• Sternberg, Shlomo (1994), Teoría de grupos y física , Cambridge University Press, ISBN 978-0-521-55885-3.
• Tung, Wu-Ki (1985). Teoría de grupos en física (1.ª ed.). Nueva Jersey·Londres·Singapur·Hong Kong: World Scientific . ISBN 978-9971966577.
• Weyl, Hermann (1928), Gruppentheorie und Quantenmechanik (La teoría de los grupos y la mecánica cuántica, traducido por HP Robertson, 1931 ed.), S. Hirzel, Leipzig (reimpreso en 1950, Dover), ISBN 978-0-486-60269-1.
• Weyl, Hermann (1946), Los grupos clásicos: sus invariantes y representaciones (2.ª ed.), Princeton University Press (reimpreso en 1997), ISBN 978-0-691-05756-9.
• Wigner, Eugene P. (1939), "Sobre representaciones unitarias del grupo de Lorentz no homogéneo", Annals of Mathematics , 40 (1): 149–204, Bibcode :1939AnMat..40..149W, doi :10.2307/1968551, JSTOR  1968551, S2CID  121773411.

• "Teoría de la representación", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Alexander Kirillov Jr. , Introducción a los grupos de Lie y álgebras de Lie (2008). Libro de texto, versión preliminar en formato PDF descargable desde la página de inicio del autor.
• Kevin Hartnett, (2020), artículo sobre teoría de la representación en la revista Quanta