Poliedro cuasirregular
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
En geometría , un poliedro cuasirregular es un poliedro uniforme que tiene exactamente dos tipos de caras regulares , que se alternan alrededor de cada vértice . Son transitivos por vértice y transitivos por arista , por lo que están más cerca de los poliedros regulares que los semirregulares , que son meramente transitivos por vértice.
Sus figuras duales son transitivas por las caras y transitivas por las aristas; tienen exactamente dos tipos de figuras de vértice regulares , que se alternan alrededor de cada cara . A veces también se las considera cuasirregulares.
Sólo existen dos poliedros cuasirregulares convexos : el cuboctaedro y el icosidodecaedro . Sus nombres, dados por Kepler , provienen de reconocer que sus caras son todas las caras (giradas de forma diferente) del cubo y octaedro de doble par , en el primer caso, y del icosaedro y dodecaedro de doble par , en el segundo caso.
A estas formas que representan un par de una figura regular y su dual se les puede dar un símbolo de Schläfli vertical o r{p,q} , para representar que sus caras son todas las caras (giradas de manera diferente) tanto de la figura regular {p,q} como de la figura dual regular {q,p} . Un poliedro cuasirregular con este símbolo tendrá una configuración de vértices p.qpq (o (pq) 2 ).
De manera más general, una figura cuasirregular puede tener una configuración de vértice (pq) r , que representa r (2 o más) secuencias de las caras alrededor del vértice.
Las teselaciones del plano también pueden ser cuasirregulares, específicamente la teselación trihexagonal , con configuración de vértice (3.6) 2 . Existen otras teselaciones cuasirregulares en el plano hiperbólico, como la teselación triheptagonal , (3.7) 2 . O más generalmente: (pq) 2 , con 1/p + 1/q < 1/2 .
Los poliedros regulares y las teselaciones con un número par de caras en cada vértice también pueden considerarse cuasirregulares diferenciando entre caras del mismo orden, representándolas de forma diferente, como coloreándolas de forma alternada (sin definir ninguna orientación de superficie). Una figura regular con símbolo de Schläfli {p,q} puede considerarse cuasirregular, con configuración de vértices (pp) q/2 , si q es par.
Ejemplos:
El octaedro regular , con símbolo de Schläfli {3,4} y siendo 4 par, puede considerarse cuasirregular como un tetratetraedro (2 conjuntos de 4 triángulos del tetraedro ), con configuración de vértices (3.3) 4/2 = (3 a .3 b ) 2 , alternando dos colores de caras triangulares.
El mosaico cuadrado , con configuración de vértices 4 4 y 4 par, puede considerarse cuasirregular, con configuración de vértices (4.4) 4/2 = (4 a .4 b ) 2 , coloreada como un tablero de ajedrez .
El teselado triangular , con configuración de vértices 3 6 y 6 par, puede considerarse cuasirregular, con configuración de vértices (3.3) 6/2 = (3 a .3 b ) 3 , alternando dos colores de caras triangulares.
Construcción Wythoff
 Los poliedros regulares ( p | 2 q ) y cuasirregulares ( 2 | pq ) se crean a partir de una construcción de Wythoff con el punto generador en uno de los tres vértices del dominio fundamental. Esto define una única arista dentro del dominio fundamental. |
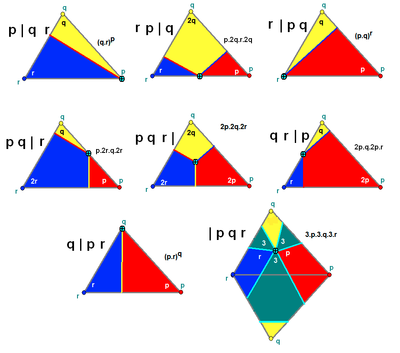
q | 2 p , p | 2 q , 2 | pq
Coxeter define un poliedro cuasirregular como uno que tiene un símbolo de Wythoff en la forma p | qr , y es regular si q=2 o q=r. [1]
El diagrama de Coxeter-Dynkin es otra representación simbólica que muestra la relación cuasirregular entre las dos formas duales-regulares:
| Símbolo de Schläfli | Diagrama de Coxeter | Símbolo de Wythoff | |
|---|---|---|---|
| {p,q} |      | q | 2 p | |
| {q,p} |      | p | 2 q | |
| r{p,q} |      o o   | 2 | pq | |
Los poliedros cuasirregulares convexos
Hay dos poliedros cuasirregulares convexos uniformes :
- El cuboctaedro , configuración de vértice (3.4) 2 , diagrama de Coxeter-Dynkin





- El icosidodecaedro , configuración de vértice (3.5) 2 , diagrama de Coxeter-Dynkin





Además, el octaedro , que también es regular , configuración de vértice (3.3) 2 , puede considerarse cuasirregular si se dan colores diferentes a las caras alternas. En esta forma, a veces se lo conoce como tetratetraedro . Los poliedros regulares convexos restantes tienen un número impar de caras en cada vértice, por lo que no se pueden colorear de una manera que preserve la transitividad de las aristas. Tiene diagrama de Coxeter-Dynkin 




Cada uno de ellos forma el núcleo común de un par dual de poliedros regulares . Los nombres de dos de ellos dan pistas sobre el par dual asociado: cubo octaedro y icosaedro dodecaedro , respectivamente . El octaedro es el núcleo común de un par dual de tetraedros (un compuesto conocido como stella octangula ); cuando se deriva de esta manera, el octaedro a veces se llama tetratetraedro , como tetraedro tetraedro .
| Regular | Doble regular | Núcleo común cuasirregular | Figura de vértice |
|---|---|---|---|
 Tetraedro {3,3}      3 | 2 3 |  Tetraedro {3,3}      3 | 2 3 |  Tetratetraedro r{3,3}      2 | 3 3 |  3.3.3.3 |
 Cubo {4,3}      3 | 2 4 |  Octaedro {3,4}      4 | 2 3 |  Cuboctaedro r{3,4}      2 | 3 4 |  3.4.3.4 |
 Dodecaedro {5,3}      3 | 2 5 |  Icosaedro {3,5}      5 | 2 3 |  Icosidodecaedro r{3,5}      2 | 3 5 |  3.5.3.5 |
Cada uno de estos poliedros cuasirregulares se puede construir mediante una operación de rectificación en cualquiera de sus padres regulares, truncando completamente los vértices, hasta que cada arista original se reduzca a su punto medio.
Teselación cuasirregular
Esta secuencia continúa como el teselado trihexagonal , figura de vértice (3.6) 2 : un teselado cuasirregular basado en el teselado triangular y el teselado hexagonal .
| Regular | Doble regular | Combinación cuasirregular | Figura de vértice |
|---|---|---|---|
 Azulejos hexagonales {6,3}      6 | 2 3 |  Teselación triangular {3,6}      3 | 2 6 |  Teselación trihexagonal r{6,3}      2 | 3 6 |  (3.6) 2 |
El patrón de tablero de ajedrez es una coloración cuasirregular del mosaico cuadrado , figura del vértice (4.4) 2 :
| Regular | Doble regular | Combinación cuasirregular | Figura de vértice |
|---|---|---|---|
 {4,4}      4 | 2 4 |  {4,4}      4 | 2 4 |  r{4,4}      2 | 4 4 |  (4.4) 2 |
El teselado triangular también puede considerarse cuasirregular, con tres conjuntos de triángulos alternados en cada vértice, (3.3) 3 :
 h{6,3} 3 | 3 3    = =     |
En el plano hiperbólico, esta secuencia continúa aún más, por ejemplo, el teselado triheptagonal , figura de vértice (3.7) 2 : un teselado cuasirregular basado en el teselado triangular de orden 7 y el teselado heptagonal .
| Regular | Doble regular | Combinación cuasirregular | Figura de vértice |
|---|---|---|---|
 Teselación heptagonal {7,3}      7 | 2 3 |  Teselación triangular {3,7}      3 | 2 7 |  Teselación triheptagonal r{3,7}      2 | 3 7 |  (3.7) 2 |
Ejemplos no convexos
Coxeter, HSM et al. (1954) también clasifican ciertos poliedros estelares , que tienen las mismas características, como cuasirregulares.
Dos se basan en pares duales de sólidos regulares de Kepler-Poinsot , de la misma manera que para los ejemplos convexos:
el gran icosidodecaedro y el dodecadodecaedro :
| Regular | Doble regular | Núcleo común cuasirregular | Figura de vértice |
|---|---|---|---|
 Gran dodecaedro estrellado { 5 / 2 ,3}        3 | 2 5/2 |  Gran icosaedro {3, 5 / 2 }        5/2 | 2 3 |  Gran icosidodecaedro r{3, 5 / 2 }        2 | 3 5/2 |  3. 5 / 2 .3. 5 / 2 |
 Dodecaedro estrellado pequeño { 5 / 2 ,5}        5 | 2 5/2 |  Gran dodecaedro {5, 5 / 2 }        5/2 | 2 5 |  Dodecadodecaedro r{5, 5 / 2 }        2 | 5 5/2 |  5. 5 / 2 .5. 5 / 2 |
Nueve más son los hemipoliedros , que son formas facetadas de los poliedros cuasirregulares antes mencionados, derivadas de la rectificación de poliedros regulares. Entre ellos se encuentran las caras ecuatoriales que pasan por el centro de los poliedros:
| Cuasiregular (rectificado) |  Tetratetraedro |  Cuboctaedro |  Icosidodecaedro |  Gran icosidodecaedro |  Dodecadodecaedro |
|---|---|---|---|---|---|
| Cuasiregulares (hemipoliedros) |  Tetrahemihexaedro 3 / 2 3 | 2 |  Octahemioctaedro 3 / 2 3 | 3 |  Icosihemidodecaedro pequeño 3 / 2 3 | 5 |  Gran icosihemidodecaedro 3 / 2 3 | 5 / 3 |  Dodecaedro pequeño 5 / 3 5 / 2 | 3 |
| Figura de vértice |  3.4.3 / 2.4 |  3.6.3 / 2.6 |  3.10.3 / 2.10 |  3. 10 / 3 . 3 / 2 . 10 / 3 |  5 / 2 .6. 5 / 3 .6 |
| Cuasiregulares (hemipoliedros) |  Cubohemioctaedro 4 / 3 4 | 3 |  Dodecahemidodecaedro pequeño 5 / 4 5 | 5 |  Gran dodecahemidodecaedro 5 / 3 5 / 2 | 5 / 3 |  Gran dodecaedro icosaedro 5 / 4 5 | 3 | |
| Figura de vértice |  4.6.4 / 3 .6 |  5.10.5 / 4.10 |  5/2 . 10/3 . 5/3 . 10 / 3 |  5.6.5 / 4.6 |
Por último hay tres formas ditrigonales , todas facetas del dodecaedro regular, cuyas figuras de vértice contienen tres alternancias de los dos tipos de caras:
| Imagen | Símbolo de Wythoff en forma facetada Diagrama de Coxeter | Figura de vértice |
|---|---|---|
 | Dodecadodecaedro ditrigonal 3 | 5/3 5  o o   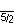  |  (5,5/3) 3 |
 | Icosidodecaedro ditrigonal pequeño 3 | 5/2 3  o o     | 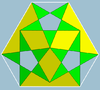 (3,5/2) 3 |
 | Gran icosidodecaedro ditrigonal 3/2 | 3 5 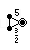 o o 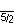    |  ((3,5) 3 )/2 |
En el plano euclídeo, la secuencia de hemipoliedros continúa con las siguientes cuatro teselaciones estrelladas, donde los apeirógonos aparecen como los polígonos ecuatoriales antes mencionados:
Duales cuasirregulares
Algunas autoridades sostienen que, puesto que los duales de los sólidos cuasirregulares comparten las mismas simetrías, estos duales también deberían llamarse cuasirregulares. Pero no todo el mundo utiliza esta terminología. Estos duales son transitivos en sus aristas y caras (pero no en sus vértices); son los sólidos Catalans transitivos en las aristas . Los convexos son, en el orden correspondiente que se indica más arriba:
- El dodecaedro rómbico , con dos tipos de vértices alternos, 8 con tres caras rómbicas y 6 con cuatro caras rómbicas.
- El triacontaedro rómbico , con dos tipos de vértices alternados, 20 con tres caras rómbicas y 12 con cinco caras rómbicas.
Además, por dualidad con el octaedro, el cubo , que habitualmente es regular , puede hacerse cuasirregular si a los vértices alternos se les dan colores diferentes.
Sus configuraciones faciales son de la forma V3.n.3.n, y diagrama de Coxeter-Dynkin 




 |  |  |  |  |  |
| Cubo V(3.3) 2      | Dodecaedro rómbico V(3,4) 2      | Triacontaedro rómbico V(3,5) 2      | Mosaico de rombos V(3.6) 2      | V(3.7) 2     | V(3.8) 2     |
Estos tres duales cuasirregulares también se caracterizan por tener caras rómbicas .
Este patrón de caras rómbicas continúa como V(3.6) 2 , el mosaico de rombos .
Politopos cuasirregulares y panales de abejas
En dimensiones superiores, Coxeter definió un politopo o panal cuasirregular como un conjunto de facetas regulares y figuras de vértices cuasirregulares. De ello se deduce que todas las figuras de vértices son congruentes y que existen dos tipos de facetas, que se alternan. [2]
En el espacio euclidiano de 4 celdas, las 16 celdas regulares también pueden verse como cuasirregulares como un teseracto alternado , h{4,3,3}, diagramas de Coxeter :





 =
=



 , compuesto por tetraedros y celdas tetraédricas alternadas . Su figura de vértice es el tetratetraedro cuasirregular (un octaedro con simetría tetraédrica),
, compuesto por tetraedros y celdas tetraédricas alternadas . Su figura de vértice es el tetratetraedro cuasirregular (un octaedro con simetría tetraédrica),



 .
.
El único panal cuasirregular en el espacio euclidiano tridimensional es el panal cúbico alternado , h{4,3,4}, diagramas de Coxeter:





 =
=



 , compuesta por celdas tetraédricas y octaédricas alternadas . Su figura de vértice es el cuboctaedro cuasirregular ,
, compuesta por celdas tetraédricas y octaédricas alternadas . Su figura de vértice es el cuboctaedro cuasirregular ,



 . [2]
. [2]
En el espacio hiperbólico tridimensional, un panal cuasirregular es el panal cúbico de orden 5 alternado , h{4,3,5}, diagramas de Coxeter:





 =
=



 , compuesta por celdas tetraédricas e icosaédricas alternadas. Su figura de vértice es el icosidodecaedro cuasirregular ,
, compuesta por celdas tetraédricas e icosaédricas alternadas. Su figura de vértice es el icosidodecaedro cuasirregular ,



 Un panal cúbico de orden 6 alternado paracompacto relacionado , h{4,3,6} tiene celdas de teselación tetraédrica y hexagonal alternadas con una figura de vértice que es una teselación trihexagonal cuasirregular .
Un panal cúbico de orden 6 alternado paracompacto relacionado , h{4,3,6} tiene celdas de teselación tetraédrica y hexagonal alternadas con una figura de vértice que es una teselación trihexagonal cuasirregular .



 .
.
| Polícoras y panales cuasirregulares: h{4,p,q} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Espacio | Finito | Afín | Compacto | Paracompacto | |||||||
Símbolo de Schläfli | h{4,3,3} | h{4,3,4} | h{4,3,5} | h{4,3,6} | h{4,4,3} | h{4,4,4} | |||||
Diagrama de Coxeter |        ↔ ↔     |        ↔ ↔     |        ↔ ↔     |        ↔ ↔     |        ↔ ↔     |        ↔ ↔     | |||||
     ↔ ↔       |    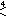  |      |      |      |      ↔ ↔       | ||||||
| Imagen |  |  |  |  | |||||||
Figura de vértice r{p,3} |       |       |       |       |       |       | |||||
Polícoras regulares o panales de la forma {p,3,4} o





 pueden tener su simetría reducida a la mitad como
pueden tener su simetría reducida a la mitad como





 en forma cuasirregular
en forma cuasirregular



 , creando celdas de colores alternados {p,3}. Estos casos incluyen el panal cúbico euclidiano {4,3,4} con celdas cúbicas , el hiperbólico compacto {5,3,4} con celdas dodecaédricas y el paracompacto {6,3,4} con celdas de mosaico hexagonal infinitas . Tienen cuatro celdas alrededor de cada borde, alternando en 2 colores. Sus figuras de vértice son tetratetraedros cuasirregulares,
, creando celdas de colores alternados {p,3}. Estos casos incluyen el panal cúbico euclidiano {4,3,4} con celdas cúbicas , el hiperbólico compacto {5,3,4} con celdas dodecaédricas y el paracompacto {6,3,4} con celdas de mosaico hexagonal infinitas . Tienen cuatro celdas alrededor de cada borde, alternando en 2 colores. Sus figuras de vértice son tetratetraedros cuasirregulares,



 =
=

 .
.



 , lo mismo que el octaedro regular
, lo mismo que el octaedro regular| Panales regulares y cuasirregulares: {p,3,4} y {p,3 1,1 } | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Espacio | Espacio euclidiano de 4 dimensiones | Espacio tridimensional euclidiano | Hiperbólico 3-espacio | ||||||||
| Nombre | {3,3,4} {3,3 1,1 } = | {4,3,4} {4,3 1,1 } = | {5,3,4} {5,3 1,1 } = | {6,3,4} {6,3 1,1 } = | |||||||
Diagrama de Coxeter |        = =     |        = =     |        = =     |        = =     | |||||||
| Imagen |  |  |  |  | |||||||
| Células {p,3} |       |       |       |       | |||||||
De manera similar, los panales hiperbólicos regulares de la forma {p,3,6} o





 pueden tener su simetría reducida a la mitad como
pueden tener su simetría reducida a la mitad como





 en forma cuasirregular
en forma cuasirregular



 , creando celdas {p,3} de colores alternados. Tienen seis celdas alrededor de cada borde, alternando en 2 colores. Sus figuras de vértice son teselas triangulares cuasirregulares .
, creando celdas {p,3} de colores alternados. Tienen seis celdas alrededor de cada borde, alternando en 2 colores. Sus figuras de vértice son teselas triangulares cuasirregulares .

 .
.





 =
=


| Forma | Paracompacto | No compacto | |||||
|---|---|---|---|---|---|---|---|
| Nombre | {3,3,6} {3,3 [3] } | {4,3,6} {4,3 [3] } | {5,3,6} {5,3 [3] } | {6,3,6} {6,3 [3] } | {7,3,6} {7,3 [3] } | {8,3,6} {8,3 [3] } | ... {∞,3,6} {∞,3 [3] } |
            |             |             |             |             |             |             |             |
| Imagen |  |  |  |  |  |  |  |
| Células |  {3,3}      |  {4,3}      |  {5,3}      |  {6,3}      |  {7,3}      |  {8,3}      |  {∞,3}      |
Véase también
Notas
- ^ Coxeter, HSM , Longuet-Higgins, MS y Miller, JCP Uniform Polyhedra, Philosophical Transactions of the Royal Society of London 246 A (1954), págs. 401–450. (Sección 7, Los poliedros regulares y cuasirregulares p | qr )
- ^ ab Coxeter, Politopos regulares, 4.7 Otros panales. p.69, p.88
Referencias
- Cromwell, P. Polihedros , Cambridge University Press (1977).
- Coxeter , Regular Polytopes (3.ª edición, 1973), edición Dover, ISBN 0-486-61480-8 , 2.3 Quasi-Regular Polyhedra (p. 17), Panales de abejas cuasirregulares, p. 69
Enlaces externos
- Weisstein, Eric W. "Poliedro cuasiregular". MundoMatemático .
- Weisstein, Eric W. "Poliedro uniforme". MundoMatemático .Poliedros cuasirregulares: (pq) r
- George Hart, Poliedros cuasirregulares