Óptica no lineal

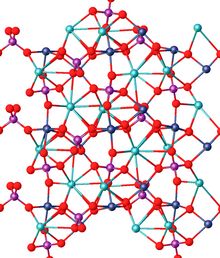
La óptica no lineal ( NLO ) es la rama de la óptica que describe el comportamiento de la luz en medios no lineales , es decir, medios en los que la densidad de polarización P responde de forma no lineal al campo eléctrico E de la luz. La no linealidad se observa típicamente solo a intensidades de luz muy altas (cuando el campo eléctrico de la luz es >10 ⁸ V/m y, por lo tanto, comparable al campo eléctrico atómico de ~10 ¹¹ V/m) como las proporcionadas por los láseres . Por encima del límite de Schwinger , se espera que el vacío en sí mismo se vuelva no lineal. En la óptica no lineal, el principio de superposición ya no se cumple. ^{[1] [2] [3]}

El primer efecto óptico no lineal que se predijo fue la absorción de dos fotones , por Maria Goeppert Mayer para su doctorado en 1931, pero permaneció como una curiosidad teórica inexplorada hasta 1961 y la observación casi simultánea de la absorción de dos fotones en Bell Labs ^[4] y el descubrimiento de la generación de segundos armónicos por Peter Franken et al. en la Universidad de Michigan , ambos poco después de la construcción del primer láser por Theodore Maiman . ^[5] Sin embargo, algunos efectos no lineales se descubrieron antes del desarrollo del láser. ^[6] La base teórica para muchos procesos no lineales se describió por primera vez en la monografía de Bloembergen "Óptica no lineal". ^[7]

La óptica no lineal explica la respuesta no lineal de propiedades como la frecuencia , la polarización, la fase o la trayectoria de la luz incidente. ^[5] Estas interacciones no lineales dan lugar a una serie de fenómenos ópticos:

• Generación de segundo armónico (SHG), o duplicación de frecuencia , generación de luz con una frecuencia duplicada (la mitad de la longitud de onda), se destruyen dos fotones, creando un solo fotón con el doble de frecuencia.
• Generación de tercer armónico (THG), generación de luz con una frecuencia triplicada (un tercio de la longitud de onda), se destruyen tres fotones, creando un solo fotón con tres veces la frecuencia.
• Generación de altos armónicos (HHG), generación de luz con frecuencias mucho mayores que las originales (normalmente de 100 a 1000 veces mayores).
• Generación de suma de frecuencias (SFG), generación de luz con una frecuencia que es la suma de otras dos frecuencias (SHG es un caso especial de esto).
• Generación de diferencia de frecuencia (DFG), generación de luz con una frecuencia que es la diferencia entre otras dos frecuencias.
• Amplificación paramétrica óptica (OPA), amplificación de una señal de entrada en presencia de una onda de bombeo de mayor frecuencia, generando al mismo tiempo una onda inactiva (puede considerarse como DFG).
• Oscilación paramétrica óptica (OPO), generación de una señal y una onda intermedia utilizando un amplificador paramétrico en un resonador (sin entrada de señal).
• Generación paramétrica óptica (OPG), como la oscilación paramétrica pero sin resonador, utilizando en su lugar una ganancia muy alta.
• Generación de semiarmónicos , el caso especial de OPO u OPG cuando la señal y el inactivo degeneran en una sola frecuencia,
• Conversión descendente paramétrica espontánea (SPDC), la amplificación de las fluctuaciones de vacío en el régimen de baja ganancia.
• Rectificación óptica (OR), generación de campos eléctricos cuasiestáticos.
• Interacción no lineal de luz y materia con electrones libres y plasmas. ^{[8] [9] [10] [11]}

• Efecto Kerr óptico , índice de refracción dependiente de la intensidad ( efecto a).${\displaystyle \chi ^{(3)}}$
• Autoenfoque , un efecto debido al efecto Kerr óptico (y posiblemente a no linealidades de orden superior) causado por la variación espacial en la intensidad que crea una variación espacial en el índice de refracción.
• Bloqueo de modo de lente Kerr (KLM), el uso del autoenfoque como mecanismo para bloquear el modo del láser.
• Modulación de autofase (SPM), un efecto debido al efecto Kerr óptico (y posiblemente a no linealidades de orden superior) causado por la variación temporal en la intensidad que crea una variación temporal en el índice de refracción.
• Solitones ópticos , una solución de equilibrio para un pulso óptico (solitón temporal) o un modo espacial (solitón espacial) que no cambia durante la propagación debido a un equilibrio entre la dispersión y el efecto Kerr (por ejemplo, modulación de autofase para solitones temporales y autoenfoque para solitones espaciales).
• Autodifracción, división de haces en un proceso de mezcla de múltiples ondas con transferencia de energía potencial. ^[12]
• Modulación de fase cruzada (XPM), donde una longitud de onda de luz puede afectar la fase de otra longitud de onda de luz a través del efecto óptico Kerr.
• La mezcla de cuatro ondas (FWM) también puede surgir de otras no linealidades.
• Generación de ondas polarizadas cruzadas (XPW), efecto en el que se genera una onda con vector de polarización perpendicular al de entrada.${\displaystyle \chi ^{(3)}}$
• Inestabilidad modulacional . ^[13]
• Amplificación Raman ^[14]
• Conjugación de fase óptica .
• Dispersión de Brillouin estimulada , interacción de fotones con fonones acústicos
• Absorción multifotónica , absorción simultánea de dos o más fotones, transfiriendo la energía a un solo electrón.
• Fotoionización múltiple , eliminación casi simultánea de muchos electrones unidos por un fotón.
• Caos en los sistemas ópticos .

En estos procesos, el medio tiene una respuesta lineal a la luz, pero las propiedades del medio se ven afectadas por otras causas:

• Efecto Pockels , el índice de refracción se ve afectado por un campo eléctrico estático; se utiliza en moduladores electroópticos .
• Acústico-óptica , el índice de refracción se ve afectado por las ondas acústicas (ultrasonidos); se utiliza en moduladores acústico-ópticos .
• Dispersión Raman , interacción de fotones con fonones ópticos .

Los efectos no lineales se dividen en dos categorías cualitativamente diferentes: efectos paramétricos y no paramétricos. Una no linealidad paramétrica es una interacción en la que el estado cuántico del material no lineal no se modifica por la interacción con el campo óptico. Como consecuencia de esto, el proceso es "instantáneo". La energía y el momento se conservan en el campo óptico, lo que hace que la coincidencia de fases sea importante y dependa de la polarización. ^{[15] [16]}

Los fenómenos ópticos no lineales paramétricos e "instantáneos" (es decir, el material debe ser sin pérdidas y sin dispersión a través de las relaciones de Kramers-Kronig ), en los que los campos ópticos no son demasiado grandes , se pueden describir mediante una expansión en serie de Taylor de la densidad de polarización dieléctrica ( momento dipolar eléctrico por unidad de volumen) P ( t ) en el tiempo t en términos del campo eléctrico E ( t ):

${\displaystyle \mathbf {P} (t)=\varepsilon _ {0}\left(\chi ^{(1)}\mathbf {E} (t)+\chi ^{(2)}\mathbf {E } ^{2}(t)+\chi ^{(3)}\mathbf {E} ^{3}(t)+\ldots \right),}$

donde los coeficientes χ ^{( n )} son las susceptibilidades de orden n del medio, y la presencia de dicho término se conoce generalmente como una no linealidad de orden n . Nótese que la densidad de polarización P ( t ) y el campo eléctrico E ( t ) se consideran escalares para simplificar. En general, χ ^{( n )} es un tensor  de rango ( n + 1) que representa tanto la naturaleza dependiente de la polarización de la interacción paramétrica como las simetrías (o falta) del material no lineal.

La ecuación de onda es fundamental para el estudio de las ondas electromagnéticas . A partir de las ecuaciones de Maxwell en un espacio isótropo, que no contiene carga libre, se puede demostrar que

${\displaystyle \nabla \times \nabla \times \mathbf {E} +{\frac {n^{2}}{c^{2}}}{\frac {\partial ^{2}}{\partial t ^{2}}}\mathbf {E} =-{\frac {1}{\varepsilon _ {0}c^{2}}}{\frac {\partial ^{2}}{\partial t^{ 2}}}\mathbf {P} ^{\text{NL}},}$

donde P ^NL es la parte no lineal de la densidad de polarización , y n es el índice de refracción , que proviene del término lineal en P.

Tenga en cuenta que normalmente se puede utilizar la identidad vectorial

${\displaystyle \nabla \times \left(\nabla \times \mathbf {V} \right)=\nabla \left(\nabla \cdot \mathbf {V} \right)-\nabla ^{2}\mathbf { V} }$

y la ley de Gauss (suponiendo que no hay cargas libres, ),${\displaystyle \rho _{\text{libre}}=0}$

${\displaystyle \nabla \cdot \mathbf {D} =0,}$

para obtener la ecuación de onda más familiar

${\displaystyle \nabla ^{2}\mathbf {E} -{\frac {n^{2}}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{ 2}}}\mathbf {E} =\mathbf {0} .}$

Para un medio no lineal, la ley de Gauss no implica que la identidad

${\displaystyle \nabla \cdot \mathbf {E} =0}$

es cierto en general, incluso para un medio isótropo. Sin embargo, incluso cuando este término no es exactamente igual a 0, suele ser despreciablemente pequeño y, por lo tanto, en la práctica suele ignorarse, lo que nos da la ecuación de onda no lineal estándar:

${\displaystyle \nabla ^{2}\mathbf {E} -{\frac {n^{2}}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{ 2}}}\mathbf {E} ={\frac {1}{\varepsilon _ {0}c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}} }\mathbf {P} ^{\text{NL}}.}$

La ecuación de onda no lineal es una ecuación diferencial no homogénea. La solución general proviene del estudio de ecuaciones diferenciales ordinarias y se puede obtener mediante el uso de una función de Green . Físicamente, se obtienen las soluciones de onda electromagnética normal para la parte homogénea de la ecuación de onda:

${\displaystyle \nabla ^{2}\mathbf {E} -{\frac {n^{2}}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{ 2}}}\mathbf {E} =\mathbf {0},}$

y el término no homogéneo

${\displaystyle {\frac {1}{\varepsilon _{0}c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {P} ^{\text{NL}}}$

actúa como un impulsor/fuente de ondas electromagnéticas. Una de las consecuencias de esto es una interacción no lineal que da como resultado una mezcla o acoplamiento de energía entre diferentes frecuencias, lo que a menudo se denomina "mezcla de ondas".

En general, una no linealidad de orden n dará lugar a una mezcla de ( n  + 1) ondas. Como ejemplo, si consideramos solo una no linealidad de segundo orden (mezcla de tres ondas), entonces la polarización P toma la forma

${\displaystyle \mathbf {P} ^{\text{NL}}=\varepsilon _{0}\chi ^{(2)}\mathbf {E} ^{2}(t).}$

Si suponemos que E ( t ) está formada por dos componentes en las frecuencias ω ₁ y ω ₂ , podemos escribir E ( t ) como

${\displaystyle \mathbf {E} (t)=E_{1}\cos(\omega _{1}t)+E_{2}\cos(\omega _{2}t),}$

y usando la fórmula de Euler para convertir a exponenciales,

${\displaystyle \mathbf {E} (t)={\frac {1}{2}}E_{1}e^{-i\omega _{1}t}+{\frac {1}{2}}E_{2}e^{-i\omega _{2}t}+{\text{c.c.}},}$

donde "cc" representa el conjugado complejo . Si introducimos esto en la expresión para P obtenemos

${\displaystyle {\begin{aligned}\mathbf {P} ^{\text{NL}}&=\varepsilon _{0}\chi ^{(2)}\mathbf {E} ^{2}(t)\\[3pt]&={\frac {\varepsilon _{0}}{4}}\chi ^{(2)}\left[{E_{1}}^{2}e^{-i2\omega _{1}t}+{E_{2}}^{2}e^{-i2\omega _{2}t}+2E_{1}E_{2}e^{-i(\omega _{1}+\omega _{2})t}+2E_{1}{E_{2}}^{*}e^{-i(\omega _{1}-\omega _{2})t}+\left(\left|E_{1}\right|^{2}+\left|E_{2}\right|^{2}\right)e^{0}+{\text{c.c.}}\right],\end{aligned}}}$

que tiene componentes de frecuencia en 2 ω ₁ , 2 ω ₂ , ω ₁  +  ω ₂ , ω ₁  −  ω ₂ y 0. Estos procesos de mezcla de tres ondas corresponden a los efectos no lineales conocidos como generación de segundo armónico , generación de suma de frecuencias , generación de diferencia de frecuencias y rectificación óptica respectivamente.

Nota: La generación y amplificación paramétricas es una variante de la generación por diferencia de frecuencias, en la que la frecuencia más baja de uno de los dos campos generadores es mucho más débil (amplificación paramétrica) o completamente inexistente (generación paramétrica). En este último caso, la incertidumbre fundamental de la mecánica cuántica en el campo eléctrico inicia el proceso.

Lo anterior ignora la dependencia de la posición de los campos eléctricos. En una situación típica, los campos eléctricos son ondas viajeras descritas por

${\displaystyle E_{j}(\mathbf {x} ,t)=E_{j,0}e^{i(\mathbf {k} _{j}\cdot \mathbf {x} -\omega _{j}t)}+{\text{c.c.}}}$

en la posición , con el vector de onda , donde es la velocidad de la luz en el vacío, y es el índice de refracción del medio a la frecuencia angular . Por lo tanto, la polarización de segundo orden a la frecuencia angular es${\displaystyle \mathbf {x} }$ ${\displaystyle \|\mathbf {k} _{j}\|=\mathbf {n} (\omega _{j})\omega _{j}/c}$${\displaystyle c}$${\displaystyle \mathbf {n} (\omega _{j})}$${\displaystyle \omega _{j}}$${\displaystyle \omega _{3}=\omega _{1}+\omega _{2}}$

${\displaystyle P^{(2)}(\mathbf {x} ,t)\propto E_{1}^{n_{1}}E_{2}^{n_{2}}e^{i[(\mathbf {k} _{1}+\mathbf {k} _{2})\cdot \mathbf {x} -\omega _{3}t]}+{\text{c.c.}}}$

En cada posición dentro del medio no lineal, la polarización oscilante de segundo orden irradia a una frecuencia angular y un vector de onda correspondiente . La interferencia constructiva, y por lo tanto un campo de alta intensidad , ocurrirá solo si${\displaystyle \mathbf {x} }$${\displaystyle \omega _{3}}$${\displaystyle \|\mathbf {k} _{3}\|=\mathbf {n} (\omega _{3})\omega _{3}/c}$${\displaystyle \omega _{3}}$

${\displaystyle {\vec {\mathbf {k} }}_{3}={\vec {\mathbf {k} }}_{1}+{\vec {\mathbf {k} }}_{2}.}$

La ecuación anterior se conoce como condición de coincidencia de fase . Normalmente, la mezcla de tres ondas se realiza en un material cristalino birrefringente, donde el índice de refracción depende de la polarización y la dirección de la luz que pasa a través de él. Las polarizaciones de los campos y la orientación del cristal se eligen de modo que se cumpla la condición de coincidencia de fase. Esta técnica de coincidencia de fase se denomina sintonización angular. Normalmente, un cristal tiene tres ejes, uno o dos de los cuales tienen un índice de refracción diferente al de los otros. Los cristales uniaxiales, por ejemplo, tienen un único eje preferido, llamado eje extraordinario (e), mientras que los otros dos son ejes ordinarios (o) (consulte óptica de cristales ). Existen varios esquemas para elegir las polarizaciones para este tipo de cristal. Si la señal y el inactivo tienen la misma polarización, se denomina "coincidencia de fase de tipo I", y si sus polarizaciones son perpendiculares, se denomina "coincidencia de fase de tipo II". Sin embargo, existen otras convenciones que especifican además qué frecuencia tiene qué polarización en relación con el eje del cristal. Estos tipos se enumeran a continuación, con la convención de que la longitud de onda de la señal es más corta que la longitud de onda inactiva.

Tipos de coincidencia de fases

( )${\displaystyle \lambda _{p}\leq \lambda _{s}\leq \lambda _{i}}$

Polarizaciones			Esquema
Bomba	Señal	Ocioso
mi	o	o	Tipo I
mi	o	mi	Tipo II (o IIA)
mi	mi	o	Tipo III (o IIB)
mi	mi	mi	Tipo IV
o	o	o	Tipo V (o tipo 0, [18] o "cero")
o	o	mi	Tipo VI (o IIB o IIIA)
o	mi	o	Tipo VII (o IIA o IIIB)
o	mi	mi	Tipo VIII (o I)

Los cristales no lineales más comunes son uniaxiales negativos, lo que significa que el eje e tiene un índice de refracción menor que el eje o . En esos cristales, los esquemas de emparejamiento de fases de tipo I y II suelen ser los más adecuados. En los cristales uniaxiales positivos, los tipos VII y VIII son más adecuados. Los tipos II y III son esencialmente equivalentes, excepto que los nombres de señal y de inactivo se intercambian cuando la señal tiene una longitud de onda mayor que la del inactivo. Por esta razón, a veces se los llama IIA y IIB. Los números de tipo V–VIII son menos comunes que I y II y sus variantes.

Un efecto indeseable de la sintonización angular es que las frecuencias ópticas involucradas no se propagan de manera colineal entre sí. Esto se debe al hecho de que la onda extraordinaria que se propaga a través de un cristal birrefringente posee un vector de Poynting que no es paralelo al vector de propagación. Esto provocaría una desviación del haz, lo que limita la eficiencia de conversión óptica no lineal. Otros dos métodos de adaptación de fase evitan la desviación del haz al obligar a todas las frecuencias a propagarse a 90° con respecto al eje óptico del cristal. Estos métodos se denominan sintonización de temperatura y adaptación de fase cuasi .

El ajuste de temperatura se utiliza cuando la polarización de frecuencia de bombeo (láser) es ortogonal a la polarización de frecuencia de señal y de inactividad. La birrefringencia en algunos cristales, en particular el niobato de litio, depende en gran medida de la temperatura. La temperatura del cristal se controla para lograr condiciones de coincidencia de fases.

El otro método es el de cuasifilación de fase. En este método, las frecuencias implicadas no están constantemente bloqueadas en fase entre sí, sino que el eje del cristal se invierte a un intervalo regular Λ, normalmente de 15 micrómetros de longitud. Por lo tanto, estos cristales se denominan periódicamente polarizados . Esto da como resultado que la respuesta de polarización del cristal vuelva a estar en fase con el haz de bombeo invirtiendo la susceptibilidad no lineal. Esto permite un flujo de energía positiva neta desde la bomba hacia la señal y las frecuencias inactivas. En este caso, el propio cristal proporciona el vector de onda adicional k  = 2π/Λ (y, por lo tanto, el momento) para satisfacer la condición de coincidencia de fase. La cuasifilación de fase se puede ampliar a rejillas chirriantes para obtener más ancho de banda y dar forma a un pulso SHG como se hace en un deslumbrador . La SHG de una bomba y la modulación de fase propia (emulada por procesos de segundo orden) de la señal y un amplificador paramétrico óptico se pueden integrar monolíticamente.

Lo anterior es válido para los procesos. Puede extenderse a los procesos donde es distinto de cero, algo que generalmente es cierto en cualquier medio sin restricciones de simetría; en particular, la mezcla de frecuencias de suma o diferencia mejorada resonantemente en gases se utiliza con frecuencia para la generación de luz ultravioleta extrema o de "vacío" . ^[19] En escenarios comunes, como la mezcla en gases diluidos, la no linealidad es débil y, por lo tanto, los rayos de luz se enfocan, lo que, a diferencia de la aproximación de onda plana utilizada anteriormente, introduce un cambio de fase pi en cada rayo de luz, lo que complica los requisitos de coincidencia de fase. ^[19] Convenientemente, la mezcla de frecuencia de diferencia con cancela este cambio de fase focal y, a menudo, tiene una condición de coincidencia de fase general casi autocancelante, lo que simplifica relativamente el ajuste de longitud de onda amplia en comparación con la generación de frecuencia de suma. ^[19] En total, las cuatro frecuencias se mezclan simultáneamente, a diferencia de la mezcla secuencial a través de dos procesos.${\displaystyle \chi ^{(2)}}$${\displaystyle \chi ^{(3)}}$${\displaystyle \chi ^{(3)}}$${\displaystyle \chi ^{(3)}}$${\displaystyle \chi ^{(2)}}$

El efecto Kerr también puede describirse como un . A altas potencias de pico, el efecto Kerr puede causar la filamentación de la luz en el aire, en la que la luz viaja sin dispersión ni divergencia en una guía de ondas autogenerada. ^[20] Incluso a altas intensidades, la serie de Taylor , que lideró el dominio de los órdenes inferiores, ya no converge y, en su lugar, se utiliza un modelo basado en el tiempo. Cuando un átomo de gas noble es golpeado por un pulso láser intenso, que tiene una intensidad de campo eléctrico comparable al campo de Coulomb del átomo, el electrón más externo puede ionizarse del átomo. Una vez liberado, el electrón puede ser acelerado por el campo eléctrico de la luz, primero alejándose del ion, luego volviendo a acercarse a él a medida que el campo cambia de dirección. El electrón puede entonces recombinarse con el ion, liberando su energía en forma de fotón. La luz se emite en cada pico del campo de luz láser que es lo suficientemente intenso, produciendo una serie de destellos de luz de attosegundos . Las energías de los fotones generadas por este proceso pueden extenderse más allá del orden armónico 800 hasta unos pocos K eV . Esto se llama generación de armónicos de alto orden . El láser debe estar polarizado linealmente, de modo que el electrón regrese a la proximidad del ion original. La generación de armónicos de alto orden se ha observado en chorros de gases nobles, celdas y guías de ondas capilares llenas de gas.${\displaystyle \chi ^{(3)}}$

Uno de los procesos de mezcla de frecuencias más utilizados es la duplicación de frecuencia o generación de segundo armónico. Con esta técnica, la salida de 1064 nm de los láseres Nd:YAG o la salida de 800 nm de los láseres Ti:zafiro se pueden convertir en luz visible, con longitudes de onda de 532 nm (verde) o 400 nm (violeta) respectivamente. ^[21]

En la práctica, la duplicación de frecuencia se lleva a cabo colocando un medio no lineal en un haz láser. Si bien existen muchos tipos de medios no lineales, los medios más comunes son los cristales. Los cristales comúnmente utilizados son BBO ( β-borato de bario ), KDP ( fosfato de potasio dihidrogenado ), KTP ( fosfato de potasio titanílico ) y niobato de litio . Estos cristales tienen las propiedades necesarias de ser fuertemente birrefringentes (necesario para obtener la coincidencia de fase, ver más abajo), tener una simetría cristalina específica, ser transparentes tanto para la luz láser incidente como para la longitud de onda de frecuencia duplicada, y tener altos umbrales de daño, lo que los hace resistentes a la luz láser de alta intensidad.

Es posible, mediante procesos ópticos no lineales, invertir exactamente la dirección de propagación y la variación de fase de un haz de luz. El haz invertido se denomina haz conjugado y, por lo tanto, la técnica se conoce como conjugación de fase óptica ^{[22] [23]} (también llamada inversión temporal , inversión del frente de onda y es significativamente diferente de la retrorreflexión ).

Un dispositivo que produce el efecto de conjugación de fase se conoce como espejo de conjugación de fase (PCM).

La conjugación de fase óptica se puede interpretar como análoga a un proceso holográfico en tiempo real . ^[24] En este caso, los haces que interactúan interactúan simultáneamente en un material óptico no lineal para formar un holograma dinámico (dos de los tres haces de entrada), o patrón de difracción en tiempo real, en el material. El tercer haz incidente difracta en este holograma dinámico y, en el proceso, lee la onda conjugada en fase . En efecto, los tres haces incidentes interactúan (esencialmente) simultáneamente para formar varios hologramas en tiempo real, lo que da como resultado un conjunto de ondas de salida difractadas que se desfasan como el haz "invertido en el tiempo". En el lenguaje de la óptica no lineal, los haces que interactúan dan como resultado una polarización no lineal dentro del material, que irradia coherentemente para formar la onda conjugada en fase.

La inversión del frente de onda significa una inversión perfecta del momento lineal y del momento angular de los fotones. La inversión del momento angular significa la inversión tanto del estado de polarización como del momento angular orbital. ^[25] La inversión del momento angular orbital del vórtice óptico se debe a la coincidencia perfecta de los perfiles de fase helicoidal de los rayos incidente y reflejado. La conjugación de fase óptica se implementa mediante dispersión Brillouin estimulada, ^[26] mezcla de cuatro ondas, mezcla de tres ondas, hologramas lineales estáticos y algunas otras herramientas.

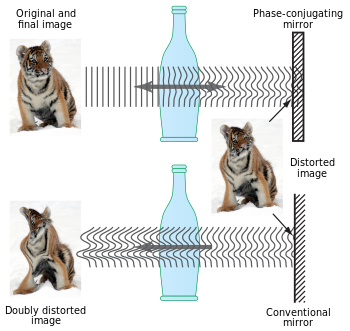
La forma más común de producir conjugación de fases ópticas es utilizar una técnica de mezcla de cuatro ondas, aunque también es posible utilizar procesos como la dispersión de Brillouin estimulada.

Para la técnica de mezcla de cuatro ondas, podemos describir cuatro haces ( j = 1, 2, 3, 4) con campos eléctricos:

${\displaystyle \Xi _{j}(\mathbf {x} ,t)={\frac {1}{2}}E_{j}(\mathbf {x} )e^{i\left(\omega _{j}t-\mathbf {k} \cdot \mathbf {x} \right)}+{\text{c.c.}},}$

donde E _j son las amplitudes del campo eléctrico. Ξ ₁ y Ξ ₂ se conocen como las dos ondas de bombeo, siendo Ξ ₃ la onda de señal y Ξ ₄ la onda conjugada generada.

Si las ondas de bombeo y la onda de señal se superponen en un medio con un χ distinto de cero ⁽³⁾ , esto produce un campo de polarización no lineal:

${\displaystyle P_{\text{NL}}=\varepsilon _{0}\chi ^{(3)}(\Xi _{1}+\Xi _{2}+\Xi _{3})^{3},}$

resultando en la generación de ondas con frecuencias dadas por ω = ±ω ₁ ± ω ₂ ± ω ₃ además de ondas de generación de tercer armónico con ω = 3ω ₁ , 3ω ₂ , 3ω ₃ .

Como se indicó anteriormente, la condición de coincidencia de fase determina cuál de estas ondas es la dominante. Al elegir condiciones tales que ω = ω ₁ + ω ₂ − ω ₃ y k = k ₁ + k ₂ − k ₃ , se obtiene un campo de polarización:

${\displaystyle P_{\omega }={\frac {1}{2}}\chi ^{(3)}\varepsilon _{0}E_{1}E_{2}E_{3}^{*}e^{i(\omega t-\mathbf {k} \cdot \mathbf {x} )}+{\text{c.c.}}}$

Este es el campo generador para el haz conjugado en fase, Ξ ₄ . Su dirección está dada por k ₄ = k ₁ + k ₂ − k ₃ , y por lo tanto, si los dos haces de bombeo se propagan en direcciones opuestas ( k ₁ = − k ₂ ), entonces los haces conjugado y de señal se propagan en direcciones opuestas ( k ₄ = − k ₃ ). Esto da como resultado la propiedad retrorreflectiva del efecto.

Además, se puede demostrar que para un medio con índice de refracción n y una longitud de interacción del haz l , la amplitud del campo eléctrico del haz conjugado se aproxima mediante

${\displaystyle E_{4}={\frac {i\omega l}{2nc}}\chi ^{(3)}E_{1}E_{2}E_{3}^{*},}$

donde c es la velocidad de la luz. Si los haces de bombeo E ₁ y E ₂ son ondas planas (contrapropagantes), entonces

${\displaystyle E_{4}(\mathbf {x} )\propto E_{3}^{*}(\mathbf {x} ),}$

Es decir, la amplitud del haz generado es el conjugado complejo de la amplitud del haz de señal. Como la parte imaginaria de la amplitud contiene la fase del haz, esto da como resultado la inversión de la propiedad de fase del efecto.

Tenga en cuenta que la constante de proporcionalidad entre la señal y los haces conjugados puede ser mayor que 1. Esto es, en efecto, un espejo con un coeficiente de reflexión mayor que el 100 %, lo que produce una reflexión amplificada. La potencia para ello proviene de los dos haces de bombeo, que se agotan durante el proceso.

La frecuencia de la onda conjugada puede ser diferente de la de la onda de señal. Si las ondas de bombeo tienen una frecuencia de ω ₁ = ω ₂ = ω, y la onda de señal tiene una frecuencia más alta, de modo que ω ₃ = ω + Δω, entonces la onda conjugada tiene una frecuencia de ω ₄ = ω − Δω. Esto se conoce como inversión de frecuencia .

En la electrodinámica clásica de Maxwell, un espejo conjugador de fase realiza la inversión del vector de Poynting :

${\displaystyle \mathbf {S} _{\text{out}}(\mathbf {r} ,t)=-\mathbf {S} _{\text{in}}(\mathbf {r} ,t),}$

("in" significa campo incidente, "out" significa campo reflejado) donde

${\displaystyle \mathbf {S} (\mathbf {r} ,t)=\epsilon _{0}c^{2}\mathbf {E} (\mathbf {r} ,t)\times \mathbf {B} (\mathbf {r} ,t),}$

que es una densidad de momento lineal del campo electromagnético. ^[25] De la misma manera, una onda conjugada en fase tiene un vector de densidad de momento angular opuesto con respecto al campo incidente: ^[26]${\displaystyle \mathbf {L} (\mathbf {r} ,t)=\mathbf {r} \times \mathbf {S} (\mathbf {r} ,t)}$

${\displaystyle \mathbf {L} _{\text{out}}(\mathbf {r} ,t)=-\mathbf {L} _{\text{in}}(\mathbf {r} ,t).}$

Las identidades anteriores son válidas localmente , es decir, en cada punto del espacio en un momento dado para un espejo conjugador de fase ideal .${\displaystyle \mathbf {r} }$${\displaystyle t}$

En la electrodinámica cuántica el fotón con energía posee también momento lineal y momento angular, cuya proyección sobre el eje de propagación es , donde es la carga topológica del fotón, o número de vueltas, es el eje de propagación. La proyección del momento angular sobre el eje de propagación tiene valores discretos .${\displaystyle \hbar \omega }$${\displaystyle \mathbf {P} =\hbar \mathbf {k} }$${\displaystyle L_{\mathbf {z} }=\pm \hbar \ell }$${\displaystyle \ell }$${\displaystyle \mathbf {z} }$ ${\displaystyle \pm \hbar \ell }$

En la electrodinámica cuántica, la interpretación de la conjugación de fases es mucho más sencilla que en la electrodinámica clásica . El fotón reflejado desde el espejo conjugador de fases (hacia fuera) tiene direcciones opuestas de momentos lineales y angulares con respecto al fotón incidente (hacia dentro):

${\displaystyle {\begin{aligned}\mathbf {P} _{\text{out}}&=-\hbar \mathbf {k} =-\mathbf {P} _{\text{in}}=\hbar \mathbf {k} ,\\{L_{\mathbf {z} }}_{\text{out}}&=-\hbar \ell =-{L_{\mathbf {z} }}_{\text{in}}=\hbar \ell .\end{aligned}}}$

Los campos ópticos transmitidos a través de medios Kerr no lineales también pueden mostrar la formación de patrones debido a que el medio no lineal amplifica el ruido espacial y temporal. El efecto se conoce como inestabilidad de modulación óptica . ^[13] Esto se ha observado tanto en redes fotónicas fotorrefractivas ^{[28] como} en sistemas fotorreactivos ^{[30] [31] [32] [ 33]} En el último caso, la no linealidad óptica se logra mediante aumentos inducidos por la reacción en el índice de refracción ^[34] . Ejemplos de formación de patrones son los solitones espaciales y las redes de vórtices en el marco de la ecuación no lineal de Schrödinger ^{[35] [36]}

Los primeros estudios de óptica no lineal y materiales se centraron en los sólidos inorgánicos. Con el desarrollo de la óptica no lineal, se investigaron las propiedades ópticas moleculares, formando ópticas no lineales moleculares. ^[37] Los enfoques tradicionales utilizados en el pasado para mejorar las no linealidades incluyen la extensión de los sistemas π de cromóforos, el ajuste de la alternancia de longitud de enlace, la inducción de transferencia de carga intramolecular, la extensión de la conjugación en 2D y la ingeniería de distribuciones de carga multipolares. Recientemente, se propusieron muchas direcciones novedosas para mejorar la no linealidad y la manipulación de la luz, incluidos los cromóforos retorcidos, la combinación de una rica densidad de estados con alternancia de enlaces, la cascada microscópica de no linealidad de segundo orden, etc. Debido a las ventajas distinguidas, la óptica no lineal molecular se ha utilizado ampliamente en el campo de la biofotónica, incluida la bioimagen, ^{[38] [39]} fototerapia, ^[40] biodetección, ^[41] etc.

Conexión de propiedades a granel con propiedades microscópicas

La óptica molecular no lineal relaciona las propiedades ópticas de la materia a granel con sus propiedades moleculares microscópicas. Así como la polarizabilidad puede describirse como una expansión de la serie de Taylor , se puede expandir el momento dipolar inducido en potencias del campo eléctrico: , donde μ es la polarizabilidad, α es la primera hiperpolarizabilidad , β es la segunda hiperpolarizabilidad, y así sucesivamente. ^[42]${\displaystyle {\boldsymbol {\mu }}={\boldsymbol {\mu _{0}}}+\alpha \cdot {\boldsymbol {\mathrm {E} }}+{\frac {1}{2}}\beta :{\boldsymbol {\mathrm {E} }}{\boldsymbol {\mathrm {E} }}}$

Nuevos medios no lineales

Ciertos materiales moleculares tienen la capacidad de ser optimizados para su no linealidad óptica a niveles microscópicos y masivos. Debido a la deslocalización de los electrones en los enlaces π, los electrones responden más fácilmente a los campos ópticos aplicados y tienden a producir respuestas ópticas lineales y no lineales mayores que las de los enlaces simples (𝜎). En estos sistemas, la respuesta lineal escala con la longitud del sistema pi conjugado, mientras que la respuesta no lineal escala incluso más rápidamente. ^[43]

Una de las muchas aplicaciones de la óptica molecular no lineal es su uso en la bioimagen no lineal. Estos materiales no lineales, como los cromóforos multifotónicos , se utilizan como biomarcadores para la espectroscopia de dos fotones, en la que la atenuación de la intensidad de la luz incidente a medida que pasa a través de la muestra se escribe como . ^[42]${\displaystyle {-dI \over dx}={N\delta I^{2} \over \hbar \omega }}$

donde N es el número de partículas por unidad de volumen, I es la intensidad de la luz y δ es la sección transversal de absorción de dos fotones . La señal resultante adopta una forma lineal lorentziana con una sección transversal proporcional a la diferencia en los momentos dipolares de los estados fundamental y final.

Se utilizan cromóforos altamente conjugados similares con fuertes características de donante-aceptor debido a su gran diferencia en los momentos dipolares, y actualmente se están realizando esfuerzos para extender sus sistemas pi-conjugados para mejorar sus propiedades ópticas no lineales. ^[37]

Ordenado por longitud de onda de la bomba:

• 800 nm: BBO
• 806 nm: yodato de litio (LiIO ₃ )
• 860 nm: niobato de potasio (KNbO ₃ )
• 980 nm: _KNbO3
• 1064 nm: fosfato monopotásico (KH ₂ PO ₄ , KDP), triborato de litio (LBO) y borato de β-bario (BBO)
• 1300 nm: seleniuro de galio (GaSe)
• 1319 nm: KNbO ₃ , BBO, KDP, fosfato de titanilo y potasio (KTP), niobato de litio (LiNbO ₃ ), LiIO ₃ y fosfato de dihidrógeno de amonio (ADP)
• 1550 nm: fosfato de titanilo y potasio (KTP), niobato de litio (LiNbO ₃ )

• Modelo de Born-Infeld
• Propagación de filamentos
• Categoría:Materiales ópticos no lineales

• Enciclopedia de física y tecnología láser Archivado el 3 de junio de 2009 en Wayback Machine , con contenido sobre óptica no lineal, por Rüdiger Paschotta
• Una explicación intuitiva de la conjugación de fases Archivado el 8 de noviembre de 2007 en Wayback Machine
• SNLO - Software de diseño de óptica no lineal Archivado el 7 de julio de 2011 en Wayback Machine
• Presentación plenaria de Robert Boyd: Óptica cuántica no lineal: la óptica no lineal se encuentra con el mundo cuántico Archivado el 17 de marzo de 2016 en Wayback Machine. Sala de prensa de SPIE
• Boyd, RW (2020). Óptica no lineal (4.ª ed.). Academi. ISBN 978-0-12-811003-4.