Estelación final del icosaedro

Estelación final del icosaedro
Dos proyecciones ortográficas simétricas
Tipo	Icosaedro estrellado , 8.º de 59
Carácter de Euler.	Como poliedro estrella: F = 20 , E = 90 , V = 60 ( χ = −10 ) Como poliedro simple: F = 180 , E = 270 , V = 92 ( χ = 2)
Grupo de simetría	icosaédrico ( I h )
Propiedades	Como un poliedro estrellado: transitivo por vértices , transitivo por caras

En geometría , la estelación completa o final del icosaedro ^[1] es la estelación más externa del icosaedro , y es "completa" y "final" porque incluye todas las celdas del diagrama de estelación del icosaedro . Es decir, cada tres planos de las caras que se intersecan del núcleo icosaédrico se intersecan en un vértice de este poliedro o en su interior. Fue estudiado por Max Brückner después del descubrimiento del poliedro de Kepler-Poinsot . Puede considerarse un poliedro irregular, simple y estrellado .

Johannes Kepler, en su Harmonices Mundi , aplicó el proceso de estelación , reconociendo el pequeño dodecaedro estrellado y el gran dodecaedro estrellado como poliedros regulares. Sin embargo, Louis Poinsot en 1809 redescubrió dos más, el gran icosaedro y el gran dodecaedro . Esto fue demostrado por Augustin-Louis Cauchy en 1812, que solo existen cuatro poliedros estrellados regulares, conocidos como el poliedro de Kepler-Poinsot . ^[2]

Brückner (1900) extendió la teoría de la estelación más allá de las formas regulares e identificó diez estelaciones del icosaedro, incluida la estelación completa . ^[4] Wheeler (1924) publicó una lista de veinte formas de estelación (veintidós incluyendo copias reflexivas), incluyendo también la estelación completa . ^[5] HSM Coxeter , P. du Val , HT Flather y JF Petrie en su libro de 1938 The Fifty Nine Icosahedra enunciaron un conjunto de reglas de estelación para el icosaedro regular y dieron una enumeración sistemática de las cincuenta y nueve estelaciones que se ajustan a esas reglas. ^[6] La estelación completa se menciona como la octava en el libro. En el libro Polyhedron Models de Wenninger , la estelación final del icosaedro se incluye como el decimoséptimo modelo de icosaedro estrellado con número de índice W ₄₂ . ^[7]

En 1995, Andrew Hume lo denominó en su base de datos poliédrica Netlib como equidnaedro en honor al equidna u oso hormiguero espinoso, un pequeño mamífero cubierto de pelo grueso y espinas y que se acurruca en una bola para protegerse. ^[8]

La estelación de un poliedro extiende las caras de un poliedro en planos infinitos y genera un nuevo poliedro que está limitado por estos planos como caras y las intersecciones de estos planos como aristas. Los Cincuenta y nueve icosaedros enumeran las estelaciones del icosaedro regular , de acuerdo con un conjunto de reglas propuestas por JCP Miller , incluida la estelación completa . El símbolo de Du Val de la estelación completa es H , porque incluye todas las celdas en el diagrama de estelación hasta la capa "h" más externa inclusive. ^[9]

Como poliedro de superficie simple y visible, la forma exterior de la estelación final está compuesta por 180 caras triangulares, que son las regiones triangulares más externas en el diagrama de estelación. Estas se unen a lo largo de 270 aristas, que a su vez se encuentran en 92 vértices, con una característica de Euler de 2. ^[10]

Los 92 vértices se encuentran en las superficies de tres esferas concéntricas. El grupo más interno de 20 vértices forma los vértices de un dodecaedro regular; la siguiente capa de 12 forma los vértices de un icosaedro regular; y la capa exterior de 60 forma los vértices de un icosaedro truncado no uniforme. Los radios de estas esferas están en la proporción ^[11]

$${\displaystyle {\sqrt {{\frac {3}{2}}(3+{\sqrt {5}}\right)}}\,:\,{\sqrt {{\frac {1}{2}}(25+11{\sqrt {5}}\right)}}\,:\,{\sqrt {{\frac {1}{2}}(97+43{\sqrt {5}}\right)}}\,.}$$

Envolventes convexos de cada esfera de vértices

Interno	Medio	Exterior	Los tres
20 vértices	12 vértices	60 vértices	92 vértices
Dodecaedro	Icosaedro	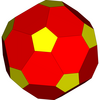Icosaedro truncado no uniforme	Icosaedro completo

Cuando se considera un objeto sólido tridimensional con longitudes de aristas , , y (donde es la proporción áurea ) el icosaedro completo tiene área de superficie ^[11]${\estilo de visualización a}$${\displaystyle \varphi a}$${\displaystyle \varphi ^{2}a}$${\displaystyle \varphi ^{2}a{\sqrt {2}}}$${\estilo de visualización \varphi}$

$${\displaystyle S={\frac {1}{20}}(13211+{\sqrt {174306161}})a^{2}\,,}$$

y volumen ^[11]

$${\displaystyle V=(210+90{\sqrt {5}})a^{3}\,.}$$

La estelación completa también puede verse como un poliedro estelar autointersecante que tiene 20 caras correspondientes a las 20 caras del icosaedro subyacente. Cada cara es un polígono estelar irregular de 9/4 , o eneagrama . ^[9] Dado que tres caras se encuentran en cada vértice, tiene 20 × 9 / 3 = 60 vértices (estos son la capa más externa de vértices visibles y forman las puntas de las "espinas") y 20 × 9 / 2 = 90 aristas (cada arista del poliedro estelar incluye y conecta dos de las 180 aristas visibles).

Considerada como un icosaedro estelar, la estelación completa es un poliedro noble , porque es a la vez isoédrico (transitivo de caras) e isogonal (transitivo de vértices).

• Con instrucciones para construir un modelo del equidnaedro ( .doc ) por Ralph Jones
• Hacia la estelación del icosaedro y el facetado del dodecaedro por Guy Inchbald
• Weisstein, Eric W. "Cincuenta y nueve estelaciones de icosaedros". MathWorld .
  • Weisstein, Eric W. "Equidnaedro". MathWorld .
• Estelaciones del icosaedro
• 59 Estelaciones del icosaedro
• Modelo VRML : http://www.georgehart.com/virtual-polyhedra/vrml/echidnahedron.wrl Archivado el 31 de diciembre de 2021 en Wayback Machine.
• Netlib : Base de datos de poliedros, modelo 141

Estelaciones notables del icosaedro
Regular	Duelos uniformes			Compuestos regulares			Estrella regular	Otros
Icosaedro (convexo)	Icosaedro triámbico pequeño	Icosaedro triámbico medial	Gran icosaedro triámbico	Compuesto de cinco octaedros	Compuesto de cinco tetraedros	Compuesto de diez tetraedros	Gran icosaedro	Dodecaedro excavado	Estelación final
El proceso de estelación en el icosaedro crea una serie de poliedros y compuestos relacionados con simetría icosaédrica .