Panal simplicial omnitruncado

En geometría, un panal simplicial omnitruncado o panal n-símplex omnitruncado es una teselación uniforme n-dimensional , basada en la simetría del grupo de Coxeter afín . Cada uno está compuesto de facetas símplex omnitruncadas . La figura del vértice para cada uno es un n-símplex irregular.${\displaystyle {\tilde {A}}_{n}}$

Las facetas de un panal simplicial omnitruncado se llaman permutaedros y pueden posicionarse en el espacio n+1 con coordenadas integrales, permutaciones de los números enteros (0,1,..,n).

norte	${\displaystyle {\tilde {A}}_{1+}}$	Imagen	Mosaico	Facetas	Figura de vértice	Figura de facetas por vértice	Vértices por figura de vértice
1	${\displaystyle {\tilde {A}}_{1}}$		Apeirogon	Segmento de línea	Segmento de línea	1	2
2	${\displaystyle {\tilde {A}}_{2}}$		Azulejos hexagonales	hexágono	Triángulo equilátero	3 hexágonos	3
3	${\displaystyle {\tilde {A}}_{3}}$		Panal cúbico bitruncado	Octaedro truncado	tetraedro irr.	4 octaedro truncado	4
4	${\displaystyle {\tilde {A}}_{4}}$		Panal de abeja 4-símplex omnitruncado	4-símplex omnitruncado	irr. 5 celdas	5 4-símplex omnitruncado	5
5	${\displaystyle {\tilde {A}}_{5}}$		Panal de abeja 5-símplex omnitruncado	5-símplex omnitruncado	irr. 5-símplex	6 5-símplex omnitruncado	6
6	${\displaystyle {\tilde {A}}_{6}}$		Panal de abeja 6-símplex omnitruncado	6-símplex omnitruncado	irr. 6-símplex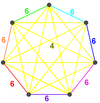	7 omnitruncado 6-símplex	7
7	${\displaystyle {\tilde {A}}_{7}}$		Panal de abeja 7-símplex omnitruncado	7-símplex omnitruncado	irr. 7-símplex	8 7-símplex omnitruncado	8
8	${\displaystyle {\tilde {A}}_{8}}$		Panal de abeja 8-símplex omnitruncado	8-símplex omnitruncado	irr. 8-símplex	9 8-símplex omnitruncado	9

Los panales (2n-1)-símplex se pueden proyectar en el panal hipercúbico omnitruncado n-dimensional mediante una operación de plegado geométrico que mapea dos pares de espejos entre sí, compartiendo la misma disposición de vértices :

${\displaystyle {\tilde {A}}_{3}}$		${\displaystyle {\tilde {A}}_{5}}$		${\displaystyle {\tilde {A}}_{7}}$		${\displaystyle {\tilde {A}}_{9}}$		...
${\displaystyle {\tilde {C}}_{2}}$		${\displaystyle {\tilde {C}}_{3}}$		${\displaystyle {\tilde {C}}_{4}}$		${\displaystyle {\tilde {C}}_{5}}$		...

• Panal hipercúbico
• Panal hipercúbico alternado
• Cuarto de panal hipercúbico
• Panal de abejas simplectico
• Panal simplicial truncado

• George Olshevsky, Tetracombs panoploides uniformes , manuscrito (2006) (lista completa de 11 teselaciónes uniformes convexas, 28 panales convexos uniformes y 143 tetracombs convexos uniformes)
• Branko Grünbaum , Teselación uniforme de espacios tridimensionales. Geombinatorics 4 (1994), 49-56.
• Manuscrito de politopos uniformes de Norman Johnson (1991)
• Coxeter, HSM Regular Polytopes , (3.ª edición, 1973), edición Dover, ISBN  0-486-61480-8
• Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
  • (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Rellenos de espacio uniformes)
  • (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]

en a mi Panales fundamentales convexos regulares y uniformes en dimensiones 2–9
Espacio	Familia	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$/ /${\displaystyle {\tilde {F}}_{4}}$${\displaystyle {\tilde {E}}_{n-1}}$
Y 2	Azulejos uniformes	0 [3]	delta 3	hδ3​	qδ3​	Hexagonal
Y 3	Panal de abeja convexo uniforme	0 [4]	delta 4	hδ4​	qδ4​
E4​	Uniforme de 4 panales	0 [5]	del 5	hδ5​	qδ5​	Panal de abeja de 24 celdas
E 5	Uniforme de 5 panales	0 [6]	delta 6	hδ6​	qδ6​
E6​	Uniforme de 6 panales	0 [7]	delta 7	hδ7​	qδ7​	2 22
E7​	Uniforme de 7 panales	0 [8]	del 8	hδ8​	qδ8​	1 33 • 3 31
E8​	Uniforme de 8 panales	0 [9]	del 9	hδ9​	qδ9​	1 52 • 2 51 • 5 21
E9​	Uniforme de 9 panales	0 [10]	delta 10	hδ10​	qδ10​
E10​	Uniforme de 10 panales	0 [11]	delta 11	hδ11​	qδ11​
En -1​	Uniforme ( n -1)- panal	0 [ n ]	delta n	hδn​	qδn​	1 k2 • 2 k1 • k21​