Mínimos cuadrados

El método de mínimos cuadrados es un método de estimación de parámetros en el análisis de regresión basado en minimizar la suma de los cuadrados de los residuos (un residuo es la diferencia entre un valor observado y el valor ajustado proporcionado por un modelo) generados en los resultados de cada ecuación individual. (En términos más simples, los mínimos cuadrados son un procedimiento matemático para encontrar la curva que mejor se ajusta a un conjunto dado de puntos al minimizar la suma de los cuadrados de los desplazamientos ("los residuos") de los puntos de la curva).

La aplicación más importante es en el ajuste de datos . Cuando el problema tiene incertidumbres sustanciales en la variable independiente (la variable x ), entonces los métodos de regresión simple y de mínimos cuadrados tienen problemas; en tales casos, se puede considerar la metodología requerida para ajustar modelos de errores en las variables en lugar de la de mínimos cuadrados.

Los problemas de mínimos cuadrados se dividen en dos categorías: mínimos cuadrados lineales u ordinarios y mínimos cuadrados no lineales , dependiendo de si las funciones del modelo son lineales o no en todas las incógnitas. El problema de mínimos cuadrados lineales se presenta en el análisis de regresión estadística ; tiene una solución de forma cerrada . El problema no lineal se resuelve generalmente mediante refinamiento iterativo ; en cada iteración, el sistema se aproxima mediante uno lineal y, por lo tanto, el cálculo central es similar en ambos casos.

Los mínimos cuadrados polinomiales describen la varianza en una predicción de la variable dependiente en función de la variable independiente y las desviaciones de la curva ajustada.

Cuando las observaciones provienen de una familia exponencial con identidad como sus estadísticas naturales suficientes y se satisfacen las condiciones suaves (por ejemplo, para distribuciones normales , exponenciales , de Poisson y binomiales ), las estimaciones de mínimos cuadrados estandarizados y las estimaciones de máxima verosimilitud son idénticas. ^[1] El método de mínimos cuadrados también se puede derivar como un estimador del método de momentos .

La siguiente discusión se presenta principalmente en términos de funciones lineales , pero el uso de mínimos cuadrados es válido y práctico para familias de funciones más generales. Además, al aplicar iterativamente la aproximación cuadrática local a la probabilidad (a través de la información de Fisher ), el método de mínimos cuadrados puede usarse para ajustar un modelo lineal generalizado .

El método de mínimos cuadrados fue descubierto y publicado oficialmente por Adrien-Marie Legendre (1805), ^[2] aunque generalmente también se le atribuye el mérito a Carl Friedrich Gauss (1809), ^{[3] [4]} quien contribuyó con importantes avances teóricos al método, ^[4] y es posible que también lo haya utilizado en su trabajo anterior en 1794 y 1795. ^{[5] [4]}

El método de mínimos cuadrados surgió en los campos de la astronomía y la geodesia , cuando los científicos y matemáticos buscaban aportar soluciones a los desafíos de navegar por los océanos de la Tierra durante la Era de los Descubrimientos . La descripción precisa del comportamiento de los cuerpos celestes fue la clave para permitir que los barcos navegaran en mar abierto, donde los marineros ya no podían confiar en las observaciones de la tierra para navegar.

El método fue la culminación de varios avances que tuvieron lugar a lo largo del siglo XVIII: ^[6]

• La combinación de diferentes observaciones como la mejor estimación del valor real; los errores disminuyen con la agregación en lugar de aumentar, tal vez expresado por primera vez por Roger Cotes en 1722.
• Combinación de diferentes observaciones realizadas en las mismas condiciones, en lugar de intentar observar y registrar con precisión una única observación. Este método se conocía como el método de los promedios. Fue utilizado en particular por Tobias Mayer al estudiar las libraciones de la Luna en 1750, y por Pierre-Simon Laplace en su trabajo para explicar las diferencias en el movimiento de Júpiter y Saturno en 1788.
• Combinación de diferentes observaciones realizadas en diferentes condiciones. El método llegó a conocerse como el método de la mínima desviación absoluta . Fue aplicado en particular por Roger Joseph Boscovich en su trabajo sobre la forma de la Tierra en 1757 y por Pierre-Simon Laplace para el mismo problema en 1789 y 1799.
• El desarrollo de un criterio que puede evaluarse para determinar cuándo se ha alcanzado la solución con el mínimo error. Laplace intentó especificar una forma matemática de la densidad de probabilidad de los errores y definir un método de estimación que minimice el error de estimación. Para este propósito, Laplace utilizó una distribución exponencial bilateral simétrica que ahora llamamos distribución de Laplace para modelar la distribución del error, y utilizó la suma de la desviación absoluta como error de estimación. Creía que estas eran las suposiciones más simples que podía hacer y esperaba obtener la media aritmética como la mejor estimación. En cambio, su estimador fue la mediana posterior.

La primera exposición clara y concisa del método de mínimos cuadrados fue publicada por Legendre en 1805. ^[7] La ​​técnica se describe como un procedimiento algebraico para ajustar ecuaciones lineales a datos y Legendre demuestra el nuevo método analizando los mismos datos que Laplace para la forma de la Tierra. En el plazo de diez años después de la publicación de Legendre, el método de mínimos cuadrados había sido adoptado como una herramienta estándar en astronomía y geodesia en Francia , Italia y Prusia , lo que constituye una aceptación extraordinariamente rápida de una técnica científica. ^[6]

En 1809 Carl Friedrich Gauss publicó su método de cálculo de las órbitas de los cuerpos celestes. En ese trabajo afirmó haber estado en posesión del método de mínimos cuadrados desde 1795. ^[8] Esto naturalmente condujo a una disputa de prioridad con Legendre. Sin embargo, para crédito de Gauss, fue más allá de Legendre y logró conectar el método de mínimos cuadrados con los principios de probabilidad y con la distribución normal . Había logrado completar el programa de Laplace de especificar una forma matemática de la densidad de probabilidad para las observaciones, dependiendo de un número finito de parámetros desconocidos, y definir un método de estimación que minimiza el error de estimación. Gauss demostró que la media aritmética es de hecho la mejor estimación del parámetro de ubicación al cambiar tanto la densidad de probabilidad como el método de estimación. Luego dio la vuelta al problema preguntando qué forma debería tener la densidad y qué método de estimación debería usarse para obtener la media aritmética como estimación del parámetro de ubicación. En este intento, inventó la distribución normal.

Una demostración temprana de la fuerza del método de Gauss se produjo cuando se utilizó para predecir la futura ubicación del recién descubierto asteroide Ceres . El 1 de enero de 1801, el astrónomo italiano Giuseppe Piazzi descubrió Ceres y pudo rastrear su trayectoria durante 40 días antes de que se perdiera en el resplandor del Sol. Basándose en estos datos, los astrónomos deseaban determinar la ubicación de Ceres después de que emergiera de detrás del Sol sin resolver las complicadas ecuaciones no lineales de Kepler del movimiento planetario. Las únicas predicciones que permitieron con éxito al astrónomo húngaro Franz Xaver von Zach reubicar a Ceres fueron las realizadas por Gauss, de 24 años, utilizando el análisis de mínimos cuadrados.

En 1810, después de leer el trabajo de Gauss, Laplace, tras demostrar el teorema del límite central , lo utilizó para justificar en una muestra grande el método de mínimos cuadrados y la distribución normal. En 1822, Gauss pudo afirmar que el enfoque de mínimos cuadrados para el análisis de regresión es óptimo en el sentido de que en un modelo lineal donde los errores tienen una media de cero, no están correlacionados, se distribuyen normalmente y tienen varianzas iguales, el mejor estimador lineal insesgado de los coeficientes es el estimador de mínimos cuadrados. Una versión extendida de este resultado se conoce como el teorema de Gauss-Markov .

La idea del análisis de mínimos cuadrados también fue formulada independientemente por el estadounidense Robert Adrian en 1808. En los dos siglos siguientes, los investigadores de la teoría de errores y de la estadística encontraron muchas formas diferentes de implementar los mínimos cuadrados. ^[9]

El objetivo consiste en ajustar los parámetros de una función modelo para que se ajusten mejor a un conjunto de datos. Un conjunto de datos simple consta de n puntos (pares de datos) , i = 1, …, n , donde es una variable independiente y es una variable dependiente cuyo valor se encuentra por observación. La función modelo tiene la forma , donde m parámetros ajustables se mantienen en el vector . El objetivo es encontrar los valores de los parámetros para el modelo que "mejor" se ajustan a los datos. El ajuste de un modelo a un punto de datos se mide por su residuo , definido como la diferencia entre el valor observado de la variable dependiente y el valor predicho por el modelo: ${\displaystyle (x_{i},y_{i})\!}$${\displaystyle x_{i}\!}$${\displaystyle y_{i}\!}$${\displaystyle f(x,{\boldsymbol {\beta }})}$${\displaystyle {\boldsymbol {\beta }}}$$${\displaystyle r_{i}=y_{i}-f(x_{i},{\boldsymbol {\beta }}).}$$

El método de mínimos cuadrados encuentra los valores óptimos de los parámetros minimizando la suma de los residuos al cuadrado : ^[10]${\displaystyle S}$$${\displaystyle S=\sum _{i=1}^{n}r_{i}^{2}.}$$

En el caso más simple , el resultado del método de mínimos cuadrados es la media aritmética de los datos de entrada.${\displaystyle f(x_{i},{\boldsymbol {\beta }})=\beta }$

Un ejemplo de un modelo en dos dimensiones es el de la línea recta. Si se denota la intersección con el eje y como y la pendiente como , la función del modelo viene dada por . Véase el ejemplo de mínimos cuadrados lineales para obtener un ejemplo completamente elaborado de este modelo.${\displaystyle \beta _{0}}$${\displaystyle \beta _{1}}$${\displaystyle f(x,{\boldsymbol {\beta }})=\beta _{0}+\beta _{1}x}$

Un punto de datos puede constar de más de una variable independiente. Por ejemplo, al ajustar un plano a un conjunto de mediciones de altura, el plano es una función de dos variables independientes, x y z , por ejemplo. En el caso más general, puede haber una o más variables independientes y una o más variables dependientes en cada punto de datos.

A la derecha hay un gráfico residual que ilustra fluctuaciones aleatorias alrededor de , lo que indica que un modelo lineal es apropiado. es una variable aleatoria independiente. ^[10]${\displaystyle r_{i}=0}$${\displaystyle (Y_{i}=\beta _{0}+\beta _{1}x_{i}+U_{i})}$${\displaystyle U_{i}}$  

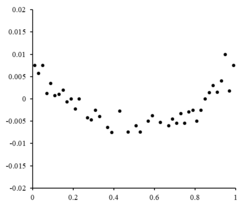
Si los puntos residuales tuvieran algún tipo de forma y no fluctuaran aleatoriamente, un modelo lineal no sería apropiado. Por ejemplo, si el gráfico de residuos tuviera una forma parabólica como se ve a la derecha, un modelo parabólico sería apropiado para los datos. Los residuos para un modelo parabólico se pueden calcular mediante . ^[10]${\displaystyle (Y_{i}=\beta _{0}+\beta _{1}x_{i}+\beta _{2}x_{i}^{2}+U_{i})}$${\displaystyle r_{i}=y_{i}-{\hat {\beta }}_{0}-{\hat {\beta }}_{1}x_{i}-{\hat {\beta }}_{2}x_{i}^{2}}$

Esta formulación de regresión considera únicamente los errores de observación en la variable dependiente (pero la regresión alternativa de mínimos cuadrados totales puede tener en cuenta los errores en ambas variables). Hay dos contextos bastante diferentes con diferentes implicaciones:

• Regresión para predicción. En este caso, se ajusta un modelo para proporcionar una regla de predicción que se pueda aplicar en una situación similar a la que se aplican los datos utilizados para el ajuste. En este caso, las variables dependientes correspondientes a esa aplicación futura estarían sujetas a los mismos tipos de error de observación que los de los datos utilizados para el ajuste. Por lo tanto, es lógicamente coherente utilizar la regla de predicción de mínimos cuadrados para esos datos.
• Regresión para ajustar una "relación verdadera". En el análisis de regresión estándar que conduce al ajuste por mínimos cuadrados, existe una suposición implícita de que los errores en la variable independiente son cero o están estrictamente controlados para que sean insignificantes. Cuando los errores en la variable independiente no son insignificantes, se pueden utilizar modelos de error de medición ; dichos métodos pueden conducir a estimaciones de parámetros , pruebas de hipótesis e intervalos de confianza que tienen en cuenta la presencia de errores de observación en las variables independientes. ^[11] Un enfoque alternativo es ajustar un modelo por mínimos cuadrados totales ; esto puede verse como la adopción de un enfoque pragmático para equilibrar los efectos de las diferentes fuentes de error al formular una función objetivo para su uso en el ajuste del modelo.

El mínimo de la suma de los cuadrados se obtiene fijando el gradiente en cero. Como el modelo contiene m parámetros, hay m ecuaciones de gradiente: y como , las ecuaciones de gradiente se convierten en$${\displaystyle {\frac {\partial S}{\partial \beta _{j}}}=2\sum _{i}r_{i}{\frac {\partial r_{i}}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m,}$$${\displaystyle r_{i}=y_{i}-f(x_{i},{\boldsymbol {\beta }})}$$${\displaystyle -2\sum _{i}r_{i}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m.}$$

Las ecuaciones de gradiente se aplican a todos los problemas de mínimos cuadrados. Cada problema particular requiere expresiones particulares para el modelo y sus derivadas parciales . ^[12]

Un modelo de regresión es lineal cuando el modelo comprende una combinación lineal de los parámetros, es decir, donde la función es una función de . ^[12]$${\displaystyle f(x,{\boldsymbol {\beta }})=\sum _{j=1}^{m}\beta _{j}\phi _{j}(x),}$$${\displaystyle \phi _{j}}$${\displaystyle x}$

Si ponemos y ponemos las variables independientes y dependientes en las matrices y , respectivamente, podemos calcular los mínimos cuadrados de la siguiente manera. Nótese que es el conjunto de todos los datos. ^{[12] [13]}${\displaystyle X_{ij}=\phi _{j}(x_{i})}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle D}$$${\displaystyle L(D,{\boldsymbol {\beta }})=\left\|Y-X{\boldsymbol {\beta }}\right\|^{2}=(Y-X{\boldsymbol {\beta }})^{\mathsf {T}}(Y-X{\boldsymbol {\beta }})=Y^{\mathsf {T}}Y-Y^{\mathsf {T}}X{\boldsymbol {\beta }}-{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}Y+{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}X{\boldsymbol {\beta }}}$$$${\displaystyle =Y^{\mathsf {T}}Y-X^{\mathsf {T}}Y{\boldsymbol {\beta }}-X^{\mathsf {T}}Y{\boldsymbol {\beta }}+X^{\mathsf {T}}X{\boldsymbol {\beta }}^{2}}$$

El gradiente de la pérdida es:$${\displaystyle {\frac {\partial L(D,{\boldsymbol {\beta }})}{\partial {\boldsymbol {\beta }}}}={\frac {\partial \left(Y^{\mathsf {T}}Y-X^{\mathsf {T}}Y{\boldsymbol {\beta }}-X^{\mathsf {T}}Y{\boldsymbol {\beta }}+X^{\mathsf {T}}X{\boldsymbol {\beta }}^{2}\right)}{\partial {\boldsymbol {\beta }}}}=-2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}}$$

Estableciendo el gradiente de la pérdida en cero y resolviendo para , obtenemos: ^{[13] [12]}${\displaystyle {\boldsymbol {\beta }}}$ $${\displaystyle -2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}=0\Rightarrow X^{\mathsf {T}}Y=X^{\mathsf {T}}X{\boldsymbol {\beta }}}$$$${\displaystyle {\boldsymbol {\hat {\beta }}}=\left(X^{\mathsf {T}}X\right)^{-1}X^{\mathsf {T}}Y}$$

En algunos casos, existe una solución cerrada para un problema de mínimos cuadrados no lineal, pero en general no la hay. En el caso de que no exista una solución cerrada, se utilizan algoritmos numéricos para encontrar el valor de los parámetros que minimiza el objetivo. La mayoría de los algoritmos implican la elección de valores iniciales para los parámetros. Luego, los parámetros se refinan iterativamente, es decir, los valores se obtienen por aproximación sucesiva: donde un superíndice k es un número de iteración y el vector de incrementos se denomina vector de desplazamiento. En algunos algoritmos de uso común, en cada iteración el modelo puede linealizarse por aproximación a una expansión de la serie de Taylor de primer orden sobre :${\displaystyle \beta }$$${\displaystyle {\beta _{j}}^{k+1}={\beta _{j}}^{k}+\Delta \beta _{j},}$$${\displaystyle \Delta \beta _{j}}$${\displaystyle {\boldsymbol {\beta }}^{k}}$$${\displaystyle {\begin{aligned}f(x_{i},{\boldsymbol {\beta }})&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}\left(\beta _{j}-{\beta _{j}}^{k}\right)\\[1ex]&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}J_{ij}\,\Delta \beta _{j}.\end{aligned}}}$$

El jacobiano J es una función de constantes, la variable independiente y los parámetros, por lo que cambia de una iteración a la siguiente. Los residuos están dados por$${\displaystyle r_{i}=y_{i}-f^{k}(x_{i},{\boldsymbol {\beta }})-\sum _{k=1}^{m}J_{ik}\,\Delta \beta _{k}=\Delta y_{i}-\sum _{j=1}^{m}J_{ij}\,\Delta \beta _{j}.}$$

Para minimizar la suma de los cuadrados de , la ecuación del gradiente se establece en cero y se resuelve para : que, al reordenar, se convierten en m ecuaciones lineales simultáneas, las ecuaciones normales :${\displaystyle r_{i}}$${\displaystyle \Delta \beta _{j}}$$${\displaystyle -2\sum _{i=1}^{n}J_{ij}\left(\Delta y_{i}-\sum _{k=1}^{m}J_{ik}\,\Delta \beta _{k}\right)=0,}$$$${\displaystyle \sum _{i=1}^{n}\sum _{k=1}^{m}J_{ij}J_{ik}\,\Delta \beta _{k}=\sum _{i=1}^{n}J_{ij}\,\Delta y_{i}\qquad (j=1,\ldots ,m).}$$

Las ecuaciones normales se escriben en notación matricial como$${\displaystyle \left(\mathbf {J} ^{\mathsf {T}}\mathbf {J} \right)\Delta {\boldsymbol {\beta }}=\mathbf {J} ^{\mathsf {T}}\Delta \mathbf {y} .}$$

Éstas son las ecuaciones definitorias del algoritmo de Gauss-Newton .

• La función modelo, f , en LLSQ (mínimos cuadrados lineales) es una combinación lineal de parámetros de la forma El modelo puede representar una línea recta, una parábola o cualquier otra combinación lineal de funciones. En NLLSQ (mínimos cuadrados no lineales) los parámetros aparecen como funciones, como y así sucesivamente. Si las derivadas son constantes o dependen solo de los valores de la variable independiente, el modelo es lineal en los parámetros. De lo contrario, el modelo es no lineal.${\displaystyle f=X_{i1}\beta _{1}+X_{i2}\beta _{2}+\cdots }$${\displaystyle \beta ^{2},e^{\beta x}}$${\displaystyle \partial f/\partial \beta _{j}}$
• Se necesitan valores iniciales para los parámetros para encontrar la solución a un problema NLLSQ; LLSQ no los requiere.
• Los algoritmos de solución para NLLSQ a menudo requieren que el jacobiano se pueda calcular de manera similar a LLSQ. Las expresiones analíticas para las derivadas parciales pueden ser complicadas. Si las expresiones analíticas son imposibles de obtener, las derivadas parciales deben calcularse mediante aproximación numérica o debe hacerse una estimación del jacobiano, a menudo mediante diferencias finitas .
• La no convergencia (falla del algoritmo para encontrar un mínimo) es un fenómeno común en NLLSQ.
• LLSQ es globalmente cóncava, por lo que la no convergencia no es un problema.
• La resolución de problemas NLLSQ suele ser un proceso iterativo que debe finalizarse cuando se satisface un criterio de convergencia. Las soluciones LLSQ se pueden calcular utilizando métodos directos, aunque los problemas con un gran número de parámetros suelen resolverse con métodos iterativos, como el método de Gauss-Seidel .
• En LLSQ la solución es única, pero en NLLSQ puede haber múltiples mínimos en la suma de cuadrados.
• Bajo la condición de que los errores no estén correlacionados con las variables predictoras, LLSQ produce estimaciones imparciales, pero incluso bajo esa condición las estimaciones NLLSQ generalmente están sesgadas.

Estas diferencias deben tenerse en cuenta siempre que se busque la solución a un problema de mínimos cuadrados no lineal. ^[12]

Consideremos un ejemplo sencillo extraído de la física. Un resorte debe obedecer la ley de Hooke , que establece que la extensión de un resorte y es proporcional a la fuerza, F , aplicada a él. constituye el modelo, donde F es la variable independiente. Para estimar la constante de fuerza , k , realizamos una serie de n mediciones con diferentes fuerzas para producir un conjunto de datos, , donde y _i es una extensión de resorte medida. ^[14] Cada observación experimental contendrá algún error, , y por lo tanto podemos especificar un modelo empírico para nuestras observaciones,$${\displaystyle y=f(F,k)=kF}$$${\displaystyle (F_{i},y_{i}),\ i=1,\dots ,n\!}$${\displaystyle \varepsilon }$$${\displaystyle y_{i}=kF_{i}+\varepsilon _{i}.}$$

Existen muchos métodos que podemos utilizar para estimar el parámetro desconocido k . Dado que las n ecuaciones en las m variables de nuestros datos comprenden un sistema sobredeterminado con una incógnita y n ecuaciones, estimamos k utilizando mínimos cuadrados. La suma de cuadrados que se debe minimizar es ^[12]$${\displaystyle S=\sum _{i=1}^{n}\left(y_{i}-kF_{i}\right)^{2}.}$$

La estimación de mínimos cuadrados de la constante de fuerza, k , está dada por$${\displaystyle {\hat {k}}={\frac {\sum _{i}F_{i}y_{i}}{\sum _{i}F_{i}^{2}}}.}$$

Suponemos que al aplicar fuerza el resorte se expande. Después de haber obtenido la constante de fuerza mediante el ajuste por mínimos cuadrados, predecimos la extensión a partir de la ley de Hooke.

En un cálculo de mínimos cuadrados con pesos unitarios, o en regresión lineal, la varianza en el parámetro j ésimo, denotado , se estima usualmente con donde la varianza del error verdadero σ ² se reemplaza por una estimación, la estadística chi-cuadrado reducida , basada en el valor minimizado de la suma residual de cuadrados (función objetivo), S . El denominador, n  −  m , son los grados de libertad estadísticos ; vea los grados de libertad efectivos para generalizaciones. ^[12] C es la matriz de covarianza .${\displaystyle \operatorname {var} ({\hat {\beta }}_{j})}$$${\displaystyle \operatorname {var} ({\hat {\beta }}_{j})=\sigma ^{2}\left(\left[X^{\mathsf {T}}X\right]^{-1}\right)_{jj}\approx {\hat {\sigma }}^{2}C_{jj},}$$$${\displaystyle {\hat {\sigma }}^{2}\approx {\frac {S}{n-m}}}$$$${\displaystyle C=\left(X^{\mathsf {T}}X\right)^{-1},}$$

Si se conoce la distribución de probabilidad de los parámetros o se realiza una aproximación asintótica, se pueden hallar límites de confianza . De manera similar, se pueden realizar pruebas estadísticas sobre los residuos si se conoce o se supone la distribución de probabilidad de los residuos. Podemos derivar la distribución de probabilidad de cualquier combinación lineal de las variables dependientes si se conoce o se supone la distribución de probabilidad de los errores experimentales. La inferencia es fácil cuando se supone que los errores siguen una distribución normal, lo que implica en consecuencia que las estimaciones de los parámetros y los residuos también se distribuirán normalmente en función de los valores de las variables independientes. ^[12]

Es necesario hacer suposiciones sobre la naturaleza de los errores experimentales para comprobar los resultados estadísticamente. Una suposición común es que los errores pertenecen a una distribución normal. El teorema del límite central respalda la idea de que esta es una buena aproximación en muchos casos.

• Teorema de Gauss-Markov . En un modelo lineal en el que los errores tienen una expectativa cero condicional a las variables independientes, no están correlacionados y tienen varianzas iguales , el mejor estimador lineal insesgado de cualquier combinación lineal de las observaciones es su estimador de mínimos cuadrados. "Mejor" significa que los estimadores de mínimos cuadrados de los parámetros tienen una varianza mínima. El supuesto de varianzas iguales es válido cuando todos los errores pertenecen a la misma distribución. ^[15]
• Si los errores pertenecen a una distribución normal, los estimadores de mínimos cuadrados son también los estimadores de máxima verosimilitud en un modelo lineal.

Sin embargo, supongamos que los errores no se distribuyen normalmente. En ese caso, un teorema de límite central a menudo implica que las estimaciones de los parámetros se distribuirán aproximadamente de manera normal siempre que la muestra sea razonablemente grande. Por esta razón, dada la importante propiedad de que la media del error es independiente de las variables independientes, la distribución del término de error no es una cuestión importante en el análisis de regresión. En concreto, no suele ser importante si el término de error sigue una distribución normal.

Un caso especial de mínimos cuadrados generalizados llamado mínimos cuadrados ponderados ocurre cuando todas las entradas fuera de la diagonal de Ω (la matriz de correlación de los residuos) son nulas; las varianzas de las observaciones (a lo largo de la diagonal de la matriz de covarianza) aún pueden ser desiguales ( heterocedasticidad ). En términos más simples, la heterocedasticidad es cuando la varianza de depende del valor de lo que hace que el gráfico de residuos cree un efecto de "despliegue" hacia valores más grandes como se ve en el gráfico de residuos a la derecha. Por otro lado, la homocedasticidad supone que la varianza de y la varianza de son iguales. ^[10]${\displaystyle Y_{i}}$${\displaystyle x_{i}}$${\displaystyle Y_{i}}$${\displaystyle Y_{i}}$${\displaystyle U_{i}}$  

El primer componente principal de la media de un conjunto de puntos se puede representar mediante la línea que más se aproxima a los puntos de datos (medida por la distancia al cuadrado del punto de aproximación más cercano, es decir, perpendicular a la línea). Por el contrario, los mínimos cuadrados lineales intentan minimizar la distancia solo en la dirección. Por lo tanto, aunque ambos utilizan una métrica de error similar, los mínimos cuadrados lineales son un método que trata una dimensión de los datos de manera preferencial, mientras que el PCA trata todas las dimensiones por igual.${\displaystyle y}$

La destacada estadística Sara van de Geer utilizó la teoría de procesos empíricos y la dimensión de Vapnik-Chervonenkis para demostrar que un estimador de mínimos cuadrados puede interpretarse como una medida en el espacio de funciones integrables al cuadrado . ^[16]

En algunos contextos, puede ser preferible una versión regularizada de la solución de mínimos cuadrados. La regularización de Tikhonov (o regresión de cresta ) agrega una restricción de que , la norma al cuadrado del vector de parámetros, no es mayor que un valor dado a la formulación de mínimos cuadrados, lo que conduce a un problema de minimización restringida. Esto es equivalente al problema de minimización sin restricciones donde la función objetivo es la suma residual de cuadrados más un término de penalización y es un parámetro de ajuste (esta es la forma lagrangiana del problema de minimización restringida). ^[17]${\displaystyle \left\|\beta \right\|_{2}^{2}}$${\displaystyle \ell _{2}}$${\displaystyle \alpha \left\|\beta \right\|_{2}^{2}}$${\displaystyle \alpha }$

En un contexto bayesiano , esto equivale a colocar una distribución normal a priori con media cero en el vector de parámetros.

Una versión regularizada alternativa de mínimos cuadrados es Lasso (operador de selección y contracción mínima absoluta), que utiliza la restricción de que , la norma L ₁ del vector de parámetros, no es mayor que un valor dado. ^{[18] [19] [20]} (Se puede demostrar como arriba usando multiplicadores de Lagrange que esto es equivalente a una minimización sin restricciones de la penalización de mínimos cuadrados con agregado). En un contexto bayesiano , esto es equivalente a colocar una distribución previa de Laplace de media cero en el vector de parámetros. ^[21] El problema de optimización se puede resolver usando programación cuadrática o métodos de optimización convexa más generales , así como también mediante algoritmos específicos como el algoritmo de regresión de ángulo mínimo .${\displaystyle \|\beta \|_{1}}$${\displaystyle \alpha \|\beta \|_{1}}$

Una de las principales diferencias entre Lasso y la regresión de cresta es que en la regresión de cresta, a medida que aumenta la penalización, todos los parámetros se reducen sin dejar de ser distintos de cero, mientras que en Lasso, al aumentar la penalización, cada vez más parámetros se reducen a cero. Esta es una ventaja de Lasso sobre la regresión de cresta, ya que reducir los parámetros a cero deselecciona las características de la regresión. Por lo tanto, Lasso selecciona automáticamente las características más relevantes y descarta las demás, mientras que la regresión de cresta nunca descarta ninguna característica por completo. Algunas técnicas de selección de características se desarrollan en base a LASSO, incluyendo Bolasso, que realiza un bootstrap de muestras, ^[22] y FeaLect, que analiza los coeficientes de regresión correspondientes a diferentes valores de para puntuar todas las características. ^[23]${\displaystyle \alpha }$

La formulación L ^{1 -regularizada es útil en algunos contextos debido a su tendencia a preferir soluciones donde más parámetros son cero, lo que da soluciones que dependen de menos variables. [18]} Por esta razón, el Lasso y sus variantes son fundamentales para el campo de la detección comprimida . Una extensión de este enfoque es la regularización de red elástica .

• Björck, Å. (1996). Métodos numéricos para problemas de mínimos cuadrados . SIAM. ISBN 978-0-89871-360-2.
• Kariya, T.; Kurata, H. (2004). Mínimos cuadrados generalizados . Hoboken: Wiley. ISBN 978-0-470-86697-9.
• Luenberger, DG (1997) [1969]. "Estimación de mínimos cuadrados". Optimización por métodos de espacio vectorial . Nueva York: John Wiley & Sons. pp. 78–102. ISBN 978-0-471-18117-0.
• Rao, CR ; Toutenburg, H.; et al. (2008). Modelos lineales: mínimos cuadrados y alternativas. Springer Series in Statistics (3.ª ed.). Berlín: Springer. ISBN 978-3-540-74226-5.
• Van de moortel, Koen (abril de 2021). "Análisis de regresión multidireccional".
• Wolberg, J. (2005). Análisis de datos mediante el método de mínimos cuadrados: extracción de la mayor cantidad de información de los experimentos . Berlín: Springer. ISBN 978-3-540-25674-8.

• Medios relacionados con Mínimos cuadrados en Wikimedia Commons