Raíz cuadrada media

En matemáticas , la raíz cuadrada media (abreviada como RMS , RMS o rms ) de un conjunto de números es la raíz cuadrada de la media cuadrada del conjunto . ^[1] Dado un conjunto , su RMS se denota como o . La RMS también se conoce como media cuadrática (denotada como ), ^{[2] [3]} un caso especial de la media generalizada . La RMS de una función continua se denota y se puede definir en términos de una integral del cuadrado de la función.$Estilo de visualización x_{i}}$${\displaystyle x_{\mathrm {RMS}}}$${\displaystyle \mathrm {RMS} _ {x}}$$Estilo de visualización M_{2}$${\displaystyle f_{\mathrm {RMS} }}$

El valor eficaz de una corriente eléctrica alterna es igual al valor de una corriente continua constante que disiparía la misma potencia en una carga resistiva . ^[1] En la teoría de estimación , la desviación cuadrática media de un estimador mide en qué medida se desvía el estimador de los datos.

El valor RMS de un conjunto de valores (o una forma de onda de tiempo continuo ) es la raíz cuadrada de la media aritmética de los cuadrados de los valores, o el cuadrado de la función que define la forma de onda continua. En física, el valor RMS de la corriente también se puede definir como el "valor de la corriente continua que disipa la misma potencia en una resistencia".

En el caso de un conjunto de n valores , el RMS es${\displaystyle \{x_{1},x_{2},\puntos ,x_{n}\}}$

${\displaystyle x_{\text{RMS}}={\sqrt {{\frac {1}{n}}\left({x_{1}}^{2}+{x_{2}}^{2}+\cdots +{x_{n}}^{2}\right)}}.}$

La fórmula correspondiente para una función continua (o forma de onda) f ( t ) definida sobre el intervalo es${\displaystyle T_{1}\leq t\leq T_{2}}$

${\displaystyle f_{\text{RMS}}={\sqrt {{1 \sobre {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{[f(t)]}^{2}\,{\rm {d}}t}}},}$

y el RMS para una función a lo largo de todo el tiempo es

${\displaystyle f_{\text{RMS}}=\lim _{T\rightarrow \infty }{\sqrt {{1 \sobre {2T}}{\int _{-T}^{T}{[f(t)]}^{2}\,{\rm {d}}t}}}.}$

El valor RMS de una función periódica en todo el tiempo es igual al valor RMS de un período de la función. El valor RMS de una función o señal continua se puede aproximar tomando el valor RMS de una muestra que consiste en observaciones espaciadas de manera uniforme. Además, el valor RMS de varias formas de onda también se puede determinar sin cálculo , como lo demostró Cartwright. ^[4]

En el caso de la estadística RMS de un proceso aleatorio , se utiliza el valor esperado en lugar de la media.

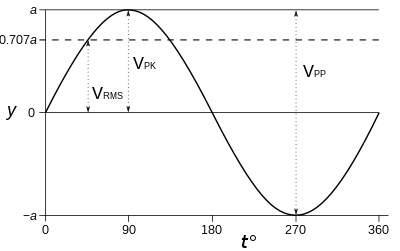
Si la forma de onda es una onda sinusoidal pura , las relaciones entre amplitudes (pico a pico, pico) y RMS son fijas y conocidas, como lo son para cualquier onda periódica continua. Sin embargo, esto no es cierto para una forma de onda arbitraria, que puede no ser periódica o continua. Para una onda sinusoidal de media cero, la relación entre RMS y amplitud pico a pico es:

De pico a pico ${\displaystyle =2{\sqrt {2}}\times {\text{RMS}}\aproximadamente 2,8\times {\text{RMS}}.}$

En el caso de otras formas de onda, las relaciones no son las mismas que en el caso de las ondas sinusoidales. Por ejemplo, para una onda triangular o en forma de diente de sierra:

De pico a pico ${\displaystyle =2{\sqrt {3}}\times {\text{RMS}}\approx 3.5\times {\text{RMS}}.}$

Forma de onda	Variables y operadores	RMS
corriente continua	${\displaystyle y=A_{0}\,}$	${\displaystyle A_{0}\,}$
Onda sinusoidal	${\displaystyle y=A_{1}\sin(2\pi ft)\,}$	${\displaystyle {\frac {A_{1}}{\sqrt {2}}}}$
Onda cuadrada	${\displaystyle y={\begin{cases}A_{1}&\operatorname {frac} (ft)<0.5\\-A_{1}&\operatorname {frac} (ft)>0.5\end{cases}}}$	${\displaystyle A_{1}\,}$
Onda cuadrada desplazada por corriente continua	${\displaystyle y=A_{0}+{\begin{cases}A_{1}&\operatorname {frac} (ft)<0.5\\-A_{1}&\operatorname {frac} (ft)>0.5\end{cases}}}$	${\displaystyle {\sqrt {A_{0}^{2}+A_{1}^{2}}}\,}$
Onda sinusoidal modificada	${\displaystyle y={\begin{cases}0&\operatorname {frac} (ft)<0.25\\A_{1}&0.25<\operatorname {frac} (ft)<0.5\\0&0.5<\operatorname {frac} (ft)<0.75\\-A_{1}&\operatorname {frac} (ft)>0.75\end{cases}}}$	${\displaystyle {\frac {A_{1}}{\sqrt {2}}}}$
Onda triangular	${\displaystyle y=\left|2A_{1}\operatorname {frac} (ft)-A_{1}\right|}$	${\displaystyle A_{1} \over {\sqrt {3}}}$
Onda de diente de sierra	${\displaystyle y=2A_{1}\operatorname {frac} (ft)-A_{1}\,}$	${\displaystyle A_{1} \over {\sqrt {3}}}$
Onda de pulso	${\displaystyle y={\begin{cases}A_{1}&\operatorname {frac} (ft)<D\\0&\operatorname {frac} (ft)>D\end{cases}}}$	${\displaystyle A_{1}{\sqrt {D}}}$
Onda sinusoidal de fase a fase	${\displaystyle y=A_{1}\sin(t)-A_{1}\sin \left(t-{\frac {2\pi }{3}}\right)\,}$	${\displaystyle A_{1}{\sqrt {\frac {3}{2}}}}$
dónde: y es desplazamiento, Es hora, f es la frecuencia, A i es la amplitud (valor pico), D es el ciclo de trabajo o la proporción del período de tiempo (1/ f ) transcurrido en alto, frac( r ) es la parte fraccionaria de r .

Las formas de onda creadas mediante la suma de formas de onda simples conocidas tienen un valor RMS que es la raíz de la suma de los cuadrados de los valores RMS de los componentes, si las formas de onda de los componentes son ortogonales (es decir, si el promedio del producto de una forma de onda simple con otra es cero para todos los pares excepto una forma de onda multiplicada por sí misma). ^[5]

${\displaystyle {\text{RMS}}_{\text{Total}}={\sqrt {{\text{RMS}}_{1}^{2}+{\text{RMS}}_{2}^{2}+\cdots +{\text{RMS}}_{n}^{2}}}}$

Alternativamente, para las formas de onda que están perfectamente correlacionadas positivamente, o "en fase" entre sí, sus valores RMS se suman directamente.

Un caso especial de RMS de combinaciones de formas de onda es: ^[6]

${\displaystyle {\text{RMS}}_{\text{AC+DC}}={\sqrt {{\text{V}}_{\text{DC}}^{2}+{\text{RMS}}_{\text{AC}}^{2}}}}$

donde se refiere al componente de corriente continua (o promedio) de la señal, y es el componente de corriente alterna de la señal.${\displaystyle {\text{V}}_{\text{DC}}}$${\displaystyle {\text{RMS}}_{\text{AC}}}$

Los ingenieros eléctricos a menudo necesitan conocer la potencia , P , disipada por una resistencia eléctrica , R. Es fácil hacer el cálculo cuando hay una corriente constante , I , a través de la resistencia. Para una carga de R ohmios, la potencia viene dada por:

${\displaystyle P=I^{2}R.}$

Sin embargo, si la corriente es una función que varía con el tiempo, I ( t ), esta fórmula debe extenderse para reflejar el hecho de que la corriente (y, por lo tanto, la potencia instantánea) varía con el tiempo. Si la función es periódica (como la corriente alterna doméstica), sigue siendo significativo analizar la potencia promedio disipada con el tiempo, que se calcula tomando la disipación de potencia promedio:

${\displaystyle {\begin{aligned}P_{\text{Avg}}&=\left(I(t)^{2}R\right)_{\text{Avg}}&&{\text{where }}(\cdots )_{\text{Avg}}{\text{ denotes the temporal mean of a function}}\\[3pt]&=\left(I(t)^{2}\right)_{\text{Avg}}R&&{\text{(as }}R{\text{ does not vary over time, it can be factored out)}}\\[3pt]&=I_{\text{RMS}}^{2}R&&{\text{by definition of root-mean-square}}\end{aligned}}}$

Por lo tanto, el valor RMS, I _RMS , de la función I ( t ) es la corriente constante que produce la misma disipación de potencia que la disipación de potencia promediada en el tiempo de la corriente I ( t ).

La potencia media también se puede encontrar utilizando el mismo método que en el caso de un voltaje variable en el tiempo , V ( t ), con valor RMS V _RMS ,

${\displaystyle P_{\text{Avg}}={V_{\text{RMS}}^{2} \over R}.}$

Esta ecuación se puede utilizar para cualquier forma de onda periódica , como una forma de onda sinusoidal o de diente de sierra , lo que nos permite calcular la potencia media suministrada a una carga específica.

Al tomar la raíz cuadrada de ambas ecuaciones y multiplicarlas entre sí, se obtiene que la potencia es:

${\displaystyle P_{\text{Avg}}=V_{\text{RMS}}I_{\text{RMS}}.}$

Ambas derivaciones dependen de que el voltaje y la corriente sean proporcionales (es decir, la carga, R , es puramente resistiva). Las cargas reactivas (es decir, cargas capaces no solo de disipar energía sino también de almacenarla) se analizan en el tema de alimentación de CA.

En el caso común de corriente alterna , cuando I ( t ) es una corriente sinusoidal , como es aproximadamente cierto para la red eléctrica, el valor RMS es fácil de calcular a partir de la ecuación del caso continuo anterior. Si I _p se define como la corriente pico, entonces:

${\displaystyle I_{\text{RMS}}={\sqrt {{1 \over {T_{2}-T_{1}}}\int _{T_{1}}^{T_{2}}\left[I_{\text{p}}\sin(\omega t)\right]^{2}dt}},}$

donde t es el tiempo y ω es la frecuencia angular ( ω  = 2 π / T , donde T es el período de la onda).

Como I _p es una constante positiva y debe elevarse al cuadrado dentro de la integral:

${\displaystyle I_{\text{RMS}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{\sin ^{2}(\omega t)}\,dt}}}.}$

Usando una identidad trigonométrica para eliminar el cuadrado de la función trigonométrica:

${\displaystyle {\begin{aligned}I_{\text{RMS}}&=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{1-\cos(2\omega t) \over 2}\,dt}}}\\[3pt]&=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{t \over 2}-{\sin(2\omega t) \over 4\omega }\right]_{T_{1}}^{T_{2}}}}\end{aligned}}}$

pero como el intervalo es un número entero de ciclos completos (según la definición de RMS), los términos seno se cancelarán, quedando:

${\displaystyle I_{\text{RMS}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{t \over 2}\right]_{T_{1}}^{T_{2}}}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{{T_{2}-T_{1}} \over 2}}}={I_{\text{p}} \over {\sqrt {2}}}.}$

Un análisis similar conduce a la ecuación análoga para el voltaje sinusoidal:

${\displaystyle V_{\text{RMS}}={V_{\text{p}} \over {\sqrt {2}}},}$

donde IP representa la corriente pico y _VP representa _el voltaje pico.

Debido a su utilidad para realizar cálculos de potencia, los voltajes listados para tomas de corriente (por ejemplo, 120  V en los EE. UU. o 230  V en Europa) casi siempre se expresan en valores RMS y no en valores pico. Los valores pico se pueden calcular a partir de los valores RMS de la fórmula anterior, que implica V _P  =  V _RMS  ×  √ 2 , suponiendo que la fuente es una onda sinusoidal pura. Por lo tanto, el valor pico del voltaje de la red en los EE. UU. es de aproximadamente 120 ×  √ 2 , o aproximadamente 170 voltios. El voltaje pico a pico, que es el doble de este, es de aproximadamente 340 voltios. Un cálculo similar indica que el voltaje pico de la red en Europa es de aproximadamente 325 voltios, y el voltaje pico a pico de la red, de aproximadamente 650 voltios.

Las magnitudes RMS, como la corriente eléctrica, se calculan normalmente a lo largo de un ciclo. Sin embargo, para algunos fines se requiere la corriente RMS a lo largo de un período más largo al calcular las pérdidas de potencia de transmisión. Se aplica el mismo principio y (por ejemplo) una corriente de 10 amperios utilizada durante 12 horas cada día de 24 horas representa una corriente media de 5 amperios, pero una corriente RMS de 7,07 amperios a largo plazo.

El término potencia RMS se utiliza a veces erróneamente (por ejemplo, en la industria del audio) como sinónimo de potencia media o potencia promedio (es proporcional al cuadrado de la tensión RMS o la corriente RMS en una carga resistiva). Para obtener una explicación de las mediciones de potencia de audio y sus deficiencias, consulte Potencia de audio .

En la física de las moléculas de gas , la velocidad cuadrática media se define como la raíz cuadrada de la velocidad cuadrática media. La velocidad RMS de un gas ideal se calcula utilizando la siguiente ecuación:

${\displaystyle v_{\text{RMS}}={\sqrt {3RT \over M}}}$

donde R representa la constante de los gases , 8,314 J/(mol·K), T es la temperatura del gas en kelvins y M es la masa molar del gas en kilogramos por mol. En física, la rapidez se define como la magnitud escalar de la velocidad. Para un gas estacionario, la rapidez media de sus moléculas puede ser del orden de miles de km/h, aunque la velocidad media de sus moléculas sea cero.

Cuando se comparan dos conjuntos de datos (uno de predicción teórica y el otro de medición real de alguna variable física, por ejemplo), el valor eficaz de las diferencias por pares de los dos conjuntos de datos puede servir como medida de qué tan lejos está, en promedio, el error de 0. La media de los valores absolutos de las diferencias por pares podría ser una medida útil de la variabilidad de las diferencias. Sin embargo, el valor eficaz de las diferencias suele ser la medida preferida, probablemente debido a la convención matemática y la compatibilidad con otras fórmulas.

El valor eficaz se puede calcular en el dominio de la frecuencia, utilizando el teorema de Parseval . Para una señal muestreada , donde es el período de muestreo,${\displaystyle x[n]=x(t=nT)}$${\displaystyle T}$

${\displaystyle \sum _{n=1}^{N}{x^{2}[n]}={\frac {1}{N}}\sum _{m=1}^{N}\left|X[m]\right|^{2},}$

donde y N es el tamaño de la muestra, es decir, el número de observaciones en la muestra y los coeficientes DFT.${\displaystyle X[m]=\operatorname {DFT} \{x[n]\}}$

En este caso, el RMS calculado en el dominio del tiempo es el mismo que en el dominio de la frecuencia:

${\displaystyle {\text{RMS}}\{x[n]\}={\sqrt {{\frac {1}{N}}\sum _{n}{x^{2}[n]}}}={\sqrt {{\frac {1}{N^{2}}}\sum _{m}{{\bigl |}X[m]{\bigr |}}^{2}}}={\sqrt {\sum _{m}{\left|{\frac {X[m]}{N}}\right|^{2}}}}.}$

Si es la media aritmética y es la desviación estándar de una población o una forma de onda , entonces: ^[7]${\displaystyle {\bar {x}}}$${\displaystyle \sigma _{x}}$

${\displaystyle x_{\text{rms}}^{2}={\overline {x}}^{2}+\sigma _{x}^{2}={\overline {x^{2}}}.}$

De esto se desprende claramente que el valor RMS es siempre mayor o igual que el promedio, ya que el RMS incluye también el "error" / desviación cuadrada.

Los científicos físicos suelen utilizar el término raíz cuadrada media como sinónimo de desviación estándar cuando se puede suponer que la señal de entrada tiene media cero, es decir, haciendo referencia a la raíz cuadrada de la desviación cuadrática media de una señal con respecto a una línea base o ajuste determinados. ^{[8] [9]} Esto resulta útil para los ingenieros eléctricos a la hora de calcular el RMS "solo CA" de una señal. Como la desviación estándar es el RMS de la variación de una señal con respecto a la media, en lugar de alrededor de 0, se elimina el componente CC (es decir, RMS(señal) = stdev(señal) si la señal media es 0).

• Adición pitagórica
• Valor rectificado medio (VRM)
• Momento central
• Media geométrica
• Norma L2
• Mínimos cuadrados
• Glosario de símbolos matemáticos
• Desplazamiento cuadrático medio
• Convertidor RMS verdadero

• Un caso de por qué el término RMS es un término inapropiado cuando se aplica a la potencia de audio
• Una aplicación Java para aprender RMS