Detección comprimida

La detección comprimida (también conocida como detección compresiva , muestreo compresivo o muestreo disperso ) es una técnica de procesamiento de señales para adquirir y reconstruir de manera eficiente una señal , mediante la búsqueda de soluciones a sistemas lineales subdeterminados . Esto se basa en el principio de que, a través de la optimización, la escasez de una señal se puede explotar para recuperarla a partir de muchas menos muestras que las requeridas por el teorema de muestreo de Nyquist-Shannon . Hay dos condiciones bajo las cuales la recuperación es posible. La primera es la escasez , que requiere que la señal sea dispersa en algún dominio. La segunda es la incoherencia, que se aplica a través de la propiedad isométrica, que es suficiente para señales dispersas. ^{[1] [2]} La detección comprimida tiene aplicaciones, por ejemplo, en la resonancia magnética, donde la condición de incoherencia generalmente se cumple. ^[3]

Un objetivo común del campo de la ingeniería de procesamiento de señales es reconstruir una señal a partir de una serie de mediciones de muestreo. En general, esta tarea es imposible porque no hay forma de reconstruir una señal durante los momentos en que no se mide la señal. Sin embargo, con conocimiento previo o suposiciones sobre la señal, resulta posible reconstruir perfectamente una señal a partir de una serie de mediciones (la adquisición de esta serie de mediciones se denomina muestreo ). Con el tiempo, los ingenieros han mejorado su comprensión de qué suposiciones son prácticas y cómo se pueden generalizar.

Un avance temprano en el procesamiento de señales fue el teorema de muestreo de Nyquist-Shannon . Este afirma que si la frecuencia más alta de una señal real es menor que la mitad de la frecuencia de muestreo, la señal puede reconstruirse perfectamente mediante interpolación sinc . La idea principal es que, con un conocimiento previo de las restricciones sobre las frecuencias de la señal, se necesitan menos muestras para reconstruir la señal.

Alrededor de 2004, Emmanuel Candès , Justin Romberg , Terence Tao y David Donoho demostraron que, dado el conocimiento sobre la escasez de una señal , la señal puede reconstruirse con incluso menos muestras de las que requiere el teorema de muestreo. ^{[4] [5]} Esta idea es la base de la detección comprimida.

La detección comprimida se basa en técnicas que varios otros campos científicos han utilizado históricamente. ^[6] En estadística, el método de mínimos cuadrados se complementó con la norma , que fue introducida por Laplace . Tras la introducción de la programación lineal y el algoritmo simplex de Dantzig , la norma se utilizó en estadística computacional . En teoría estadística, la norma fue utilizada por George W. Brown y escritores posteriores sobre estimadores imparciales de mediana . Fue utilizada por Peter J. Huber y otros que trabajaban en estadísticas robustas . La norma también se utilizó en el procesamiento de señales, por ejemplo, en la década de 1970, cuando los sismólogos construyeron imágenes de capas reflectantes dentro de la tierra basadas en datos que no parecían satisfacer el criterio de Nyquist-Shannon . ^[7] Se utilizó en la búsqueda de coincidencia en 1993, el estimador LASSO por Robert Tibshirani en 1996 ^[8] y la búsqueda de base en 1998. ^[9]$Estilo de visualización L1$$Estilo de visualización L1$$Estilo de visualización L1$$Estilo de visualización L1$$Estilo de visualización L1$

A primera vista, la detección comprimida podría parecer que viola el teorema de muestreo , porque la detección comprimida depende de la escasez de la señal en cuestión y no de su frecuencia más alta. Esto es un concepto erróneo, porque el teorema de muestreo garantiza una reconstrucción perfecta dadas las condiciones suficientes, no las necesarias. Un método de muestreo fundamentalmente diferente del muestreo de tasa fija clásico no puede "violar" el teorema de muestreo. Las señales dispersas con componentes de alta frecuencia pueden ser submuestreadas en gran medida utilizando la detección comprimida en comparación con el muestreo de tasa fija clásico. ^[10]

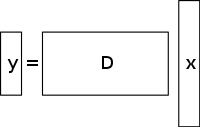
Un sistema indeterminado de ecuaciones lineales tiene más incógnitas que ecuaciones y, por lo general, tiene un número infinito de soluciones. La figura siguiente muestra un sistema de ecuaciones en el que queremos encontrar una solución para .${\displaystyle \mathbf {y} =D\mathbf {x} }$${\displaystyle \mathbf {x}}$

Para elegir una solución para un sistema de este tipo, se deben imponer restricciones o condiciones adicionales (como la suavidad) según corresponda. En la detección comprimida, se agrega la restricción de escasez, lo que permite solo soluciones que tienen una pequeña cantidad de coeficientes distintos de cero. No todos los sistemas indeterminados de ecuaciones lineales tienen una solución dispersa. Sin embargo, si existe una solución dispersa única para el sistema indeterminado, entonces el marco de detección comprimida permite la recuperación de esa solución.

La detección comprimida aprovecha la redundancia de muchas señales interesantes (no son puro ruido). En particular, muchas señales son dispersas , es decir, contienen muchos coeficientes cercanos o iguales a cero cuando se representan en algún dominio. ^[11] Esta es la misma idea que se utiliza en muchas formas de compresión con pérdida .

La detección comprimida generalmente comienza con la toma de una combinación lineal ponderada de muestras, también llamadas mediciones compresivas, en una base diferente de la base en la que se sabe que la señal es escasa. Los resultados encontrados por Emmanuel Candès , Justin Romberg , Terence Tao y David Donoho mostraron que el número de estas mediciones compresivas puede ser pequeño y aún así contener casi toda la información útil. Por lo tanto, la tarea de convertir la imagen nuevamente al dominio deseado implica resolver una ecuación matricial subdeterminada , ya que el número de mediciones compresivas tomadas es menor que el número de píxeles en la imagen completa. Sin embargo, agregar la restricción de que la señal inicial es escasa permite resolver este sistema subdeterminado de ecuaciones lineales .

La solución de mínimos cuadrados para tales problemas es minimizar la norma , es decir, minimizar la cantidad de energía en el sistema. Esto suele ser simple matemáticamente (solo implica una multiplicación de la matriz por la pseudoinversa de la base muestreada). Sin embargo, esto conduce a malos resultados para muchas aplicaciones prácticas, para las cuales los coeficientes desconocidos tienen energía distinta de cero.$Estilo de visualización L2$

Para hacer cumplir la restricción de escasez al resolver el sistema indeterminado de ecuaciones lineales, se puede minimizar el número de componentes distintos de cero de la solución. David Donoho denominó "norma" a la función que cuenta el número de componentes distintos de cero de un vector . ^{[nota 1]}$Estilo de visualización L^{0}}$

Candès et al. demostraron que para muchos problemas es probable que la norma sea equivalente a la norma , en un sentido técnico: Este resultado de equivalencia permite resolver el problema, lo cual es más fácil que el problema. Encontrar el candidato con la norma más pequeña se puede expresar con relativa facilidad como un programa lineal , para el cual ya existen métodos de solución eficientes. ^[13] Cuando las mediciones pueden contener una cantidad finita de ruido, la eliminación de ruido por búsqueda de base se prefiere a la programación lineal, ya que preserva la escasez frente al ruido y se puede resolver más rápido que un programa lineal exacto.$Estilo de visualización L1$$Estilo de visualización L^{0}}$$Estilo de visualización L1$$Estilo de visualización L^{0}}$$Estilo de visualización L1$

La variación total puede ser vista como una función real no negativa definida en el espacio de funciones reales (para el caso de funciones de una variable) o en el espacio de funciones integrables (para el caso de funciones de varias variables). Para las señales, especialmente, la variación total se refiere a la integral del gradiente absoluto de la señal. En la reconstrucción de señales e imágenes, se aplica como regularización de variación total , donde el principio subyacente es que las señales con detalles excesivos tienen una variación total alta y que la eliminación de estos detalles, al tiempo que se conserva información importante como los bordes, reduciría la variación total de la señal y haría que el sujeto de la señal se acercara más a la señal original en el problema.

Para la reconstrucción de señales e imágenes se utilizan modelos de minimización. Otros métodos incluyen también los mínimos cuadrados, como se ha comentado anteriormente en este artículo. Estos métodos son extremadamente lentos y devuelven una reconstrucción no tan perfecta de la señal. Los modelos actuales de regularización de CS intentan abordar este problema incorporando valores a priori de escasez de la imagen original, uno de los cuales es la variación total (TV). Los métodos de TV convencionales están diseñados para dar soluciones constantes por partes. Algunos de estos incluyen (como se explica más adelante) la minimización restringida, que utiliza un esquema iterativo. Este método, aunque rápido, conduce posteriormente a un suavizado excesivo de los bordes, lo que da como resultado bordes de imagen borrosos. ^[14] Se han implementado métodos de TV con reponderación iterativa para reducir la influencia de grandes magnitudes de valores de gradiente en las imágenes. Esto se ha utilizado en la reconstrucción por tomografía computarizada (TC) como un método conocido como variación total con preservación de bordes. Sin embargo, como las magnitudes de gradiente se utilizan para estimar los pesos de penalización relativos entre los términos de fidelidad de datos y regularización, este método no es robusto al ruido y los artefactos ni lo suficientemente preciso para la reconstrucción de imágenes/señales de CS y, por lo tanto, no logra preservar estructuras más pequeñas.${\displaystyle \ell _{1}}$${\textstyle \ell _{1}}$

Los avances recientes en este problema implican el uso de un refinamiento iterativo de TV direccional para la reconstrucción de CS. ^[15] Este método tendría 2 etapas: la primera etapa estimaría y refinaría el campo de orientación inicial, que se define como una estimación inicial puntual ruidosa, a través de la detección de bordes, de la imagen dada. En la segunda etapa, se presenta el modelo de reconstrucción de CS utilizando un regularizador de TV direccional. A continuación se proporcionan más detalles sobre estos enfoques basados ​​en TV (minimización l1 reponderada iterativamente, TV con preservación de bordes y modelo iterativo que utiliza campo de orientación direccional y TV).

En los modelos de reconstrucción CS que utilizan minimización restringida, ^[16] los coeficientes mayores son penalizados fuertemente en la norma. Se propuso tener una formulación ponderada de minimización diseñada para penalizar de manera más democrática los coeficientes distintos de cero. Se utiliza un algoritmo iterativo para construir los pesos apropiados. ^[17] Cada iteración requiere resolver un problema de minimización al encontrar el mínimo local de una función de penalización cóncava que se asemeje más a la norma. Se introduce un parámetro adicional, generalmente para evitar transiciones abruptas en la curva de la función de penalización, en la ecuación iterativa para asegurar la estabilidad y para que una estimación cero en una iteración no conduzca necesariamente a una estimación cero en la siguiente iteración. El método implica esencialmente usar la solución actual para calcular los pesos que se usarán en la siguiente iteración.${\displaystyle \ell _{1}}$${\displaystyle \ell _{1}}$${\displaystyle \ell _{1}}$${\displaystyle \ell _{1}}$${\displaystyle \ell _{0}}$

Las primeras iteraciones pueden encontrar estimaciones de muestra inexactas, sin embargo, este método reducirá la muestra de estas en una etapa posterior para dar más peso a las estimaciones de señal más pequeñas que no sean cero. Una de las desventajas es la necesidad de definir un punto de inicio válido, ya que es posible que no se obtenga un mínimo global cada vez debido a la concavidad de la función. Otra desventaja es que este método tiende a penalizar uniformemente el gradiente de la imagen independientemente de las estructuras de imagen subyacentes. Esto provoca un suavizado excesivo de los bordes, especialmente los de las regiones de bajo contraste, lo que posteriormente conduce a la pérdida de información de bajo contraste. Las ventajas de este método incluyen: reducción de la frecuencia de muestreo para señales dispersas; reconstrucción de la imagen al mismo tiempo que es robusta a la eliminación de ruido y otros artefactos; y uso de muy pocas iteraciones. Esto también puede ayudar a recuperar imágenes con gradientes dispersos.

En la figura que se muestra a continuación, P1 se refiere al primer paso del proceso de reconstrucción iterativa de la matriz de proyección P de la geometría de haz en abanico, que está limitada por el término de fidelidad de datos. Esto puede contener ruido y artefactos ya que no se realiza ninguna regularización. La minimización de P1 se resuelve a través del método de mínimos cuadrados de gradiente conjugado. P2 se refiere al segundo paso del proceso de reconstrucción iterativa en el que utiliza el término de regularización de variación total que preserva los bordes para eliminar el ruido y los artefactos, y así mejorar la calidad de la imagen/señal reconstruida. La minimización de P2 se realiza a través de un método simple de descenso de gradiente. La convergencia se determina probando, después de cada iteración, la positividad de la imagen, verificando si es para el caso cuando (nótese que se refiere a los diferentes coeficientes de atenuación lineal de rayos X en diferentes vóxeles de la imagen del paciente).${\displaystyle f^{k-1}=0}$${\displaystyle f^{k-1}<0}$${\estilo de visualización f}$

Este es un algoritmo iterativo de reconstrucción de TC con regularización de TV que preserva los bordes para reconstruir imágenes de TC a partir de datos altamente submuestreados obtenidos con TC de baja dosis a través de niveles bajos de corriente (miliamperios). Para reducir la dosis de imagen, uno de los enfoques utilizados es reducir la cantidad de proyecciones de rayos X adquiridas por los detectores del escáner. Sin embargo, estos datos de proyección insuficientes que se utilizan para reconstruir la imagen de TC pueden causar artefactos de rayas. Además, el uso de estas proyecciones insuficientes en algoritmos de TV estándar termina haciendo que el problema quede subdeterminado y, por lo tanto, conduce a infinitas soluciones posibles. En este método, se asigna una función ponderada de penalización adicional a la norma de TV original. Esto permite una detección más fácil de discontinuidades agudas en la intensidad de las imágenes y, por lo tanto, adapta el peso para almacenar la información de borde recuperada durante el proceso de reconstrucción de señal/imagen. El parámetro controla la cantidad de suavizado aplicado a los píxeles en los bordes para diferenciarlos de los píxeles que no están en los bordes. El valor de se cambia de forma adaptativa en función de los valores del histograma de la magnitud del gradiente, de modo que un cierto porcentaje de píxeles tienen valores de gradiente mayores que . Por lo tanto, el término de variación total que preserva los bordes se vuelve más disperso y esto acelera la implementación. Se utiliza un proceso de iteración de dos pasos conocido como algoritmo de división hacia adelante-hacia atrás. ^[18] El problema de optimización se divide en dos subproblemas que luego se resuelven con el método de mínimos cuadrados de gradiente conjugado ^[19] y el método de descenso de gradiente simple respectivamente. El método se detiene cuando se ha logrado la convergencia deseada o si se alcanza el número máximo de iteraciones. ^[14]${\estilo de visualización \sigma}$${\estilo de visualización \sigma}$${\estilo de visualización \sigma}$

Algunas de las desventajas de este método son la ausencia de estructuras más pequeñas en la imagen reconstruida y la degradación de la resolución de la imagen. Sin embargo, este algoritmo de TV que preserva los bordes requiere menos iteraciones que el algoritmo de TV convencional. ^[14] Al analizar los perfiles de intensidad horizontal y vertical de las imágenes reconstruidas, se puede ver que hay saltos bruscos en los puntos de los bordes y fluctuaciones insignificantes y menores en los puntos que no son de los bordes. Por lo tanto, este método conduce a un error relativo bajo y una correlación más alta en comparación con el método de TV. También suprime y elimina eficazmente cualquier forma de ruido de imagen y artefactos de imagen como rayas.

Para evitar el suavizado excesivo de los bordes y los detalles de la textura y obtener una imagen CS reconstruida que sea precisa y robusta al ruido y los artefactos, se utiliza este método. Primero, se obtiene una estimación inicial del campo de orientación puntual ruidoso de la imagen , . Este campo de orientación ruidoso se define de modo que se pueda refinar en una etapa posterior para reducir las influencias del ruido en la estimación del campo de orientación. Luego se introduce una estimación del campo de orientación gruesa basada en el tensor de estructura, que se formula como: ^[20] . Aquí, se refiere al tensor de estructura relacionado con el punto de píxel de la imagen (i,j) que tiene una desviación estándar . se refiere al núcleo gaussiano con desviación estándar . se refiere al parámetro definido manualmente para la imagen por debajo del cual la detección de bordes es insensible al ruido. se refiere al gradiente de la imagen y se refiere al producto tensorial obtenido al usar este gradiente. ^[15]${\displaystyle I}$${\displaystyle {\hat {d}}}$ ${\displaystyle J_{\rho}(\nabla I_{\sigma})=G_{\rho}*(\nabla I_{\sigma}\otimes \nabla I_{\sigma})={\begin{pmatrix}J_{11}&J_{12}\\J_{12}&J_{22}\end{pmatrix}}}$${\displaystyle J_{\rho}}$${\estilo de visualización \rho}$${\estilo de visualización G}$${\displaystyle (0,\rho ^{2})}$${\estilo de visualización \rho}$${\estilo de visualización \sigma}$${\displaystyle I}$${\displaystyle \nabla I_{\sigma }}$${\displaystyle I}$${\displaystyle (\nabla I_{\sigma }\otimes \nabla I_{\sigma })}$

El tensor de estructura obtenido se convoluciona con un núcleo gaussiano para mejorar la precisión de la estimación de la orientación al establecerse en valores altos para tener en cuenta los niveles de ruido desconocidos. Para cada píxel (i, j) en la imagen, el tensor de estructura J es una matriz semidefinida positiva y simétrica. Al convolucionar todos los píxeles de la imagen con , se obtienen los vectores propios ortonormales ω y υ de la matriz. ω apunta en la dirección de la orientación dominante que tiene el mayor contraste y υ apunta en la dirección de la orientación de la estructura que tiene el menor contraste. La estimación inicial aproximada del campo de orientación se define como = υ. Esta estimación es precisa en bordes fuertes. Sin embargo, en bordes débiles o en regiones con ruido, su fiabilidad disminuye.${\estilo de visualización G}$${\estilo de visualización \sigma}$${\estilo de visualización G}$${\estilo de visualización J}$${\displaystyle {\hat {d}}}$${\displaystyle {\hat {d}}}$

Para superar este inconveniente, se define un modelo de orientación refinado en el que el término de datos reduce el efecto del ruido y mejora la precisión, mientras que el segundo término de penalización con la norma L2 es un término de fidelidad que garantiza la precisión de la estimación aproximada inicial.

Este campo de orientación se introduce en el modelo de optimización de variación total direccional para la reconstrucción de CS a través de la ecuación: . es la señal objetivo que necesita ser recuperada. Y es el vector de medición correspondiente, d es el campo de orientación refinado iterativo y es la matriz de medición de CS. Este método sufre unas pocas iteraciones que finalmente conducen a la convergencia. es la estimación aproximada del campo de orientación de la imagen reconstruida a partir de la iteración anterior (para verificar la convergencia y el rendimiento óptico posterior, se utiliza la iteración anterior). Para los dos campos vectoriales representados por y , se refiere a la multiplicación de los respectivos elementos vectoriales horizontales y verticales de y seguida de su posterior adición. Estas ecuaciones se reducen a una serie de problemas de minimización convexa que luego se resuelven con una combinación de métodos de división de variables y lagrangiano aumentado (solucionador rápido basado en FFT con una solución de forma cerrada). ^[15] It (lagrangiano aumentado) se considera equivalente a la iteración de Bregman dividida que asegura la convergencia de este método. El campo de orientación, d, se define como igual a , donde define las estimaciones horizontales y verticales de .${\displaystyle \min _{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}$${\displaystyle \mathrm {X}}$${\estilo de visualización \Phi}$${\displaystyle {\hat {d}}}$$Estilo de visualización X^{k-1}}$${\displaystyle \mathrm {X}}$${\estilo de visualización d}$${\displaystyle \mathrm {X} \bullet d}$${\displaystyle \mathrm {X}}$${\estilo de visualización d}$${\displaystyle (d_{h},d_{v})}$$Estilo de visualización: d_{h},d_{v}$${\estilo de visualización d}$

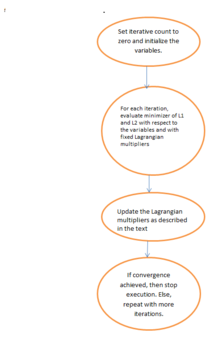
El método lagrangiano aumentado para el campo de orientación, , implica inicializar y luego encontrar el minimizador aproximado de con respecto a estas variables. Luego, los multiplicadores lagrangianos se actualizan y el proceso iterativo se detiene cuando se logra la convergencia. Para el modelo iterativo de refinamiento de variación total direccional, el método lagrangiano aumentado implica inicializar . ^[21]${\displaystyle \min _{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}$${\displaystyle d_{h},d_{v},H,V}$$Estilo de visualización L_{1}$${\displaystyle \mathrm {X} ,P,Q,\lambda _ {P},\lambda _ {Q}}$

Aquí se introducen nuevas variables donde = , = , = , y = . son los multiplicadores lagrangianos para . Para cada iteración, se calcula el minimizador aproximado de con respecto a las variables ( ). Y como en el modelo de refinamiento de campo, los multiplicadores lagrangianos se actualizan y el proceso iterativo se detiene cuando se logra la convergencia.${\estilo de visualización H, V, P, Q}$${\estilo de visualización H}$${\displaystyle \nabla d_{h}}$${\estilo de visualización V}$${\displaystyle \nabla d_{v}}$${\estilo de visualización P}$${\displaystyle \nabla \mathrm {X} }$${\estilo de visualización Q}$${\displaystyle P\bullet d}$${\displaystyle \lambda_{H},\lambda_{V},\lambda_{P},\lambda_{Q}}$${\estilo de visualización H, V, P, Q}$$Estilo de visualización L_{2}$${\displaystyle \mathrm {X}, P, Q}$

Para el modelo de refinamiento del campo de orientación, los multiplicadores lagrangianos se actualizan en el proceso iterativo de la siguiente manera:

${\displaystyle (\lambda _{H})^{k}=(\lambda _{H})^{k-1}+\gamma _{H}(H^{k}-\nabla (d_{h})^{k})}$

${\displaystyle (\lambda _{V})^{k}=(\lambda _{V})^{k-1}+\gamma _{V}(V^{k}-\nabla (d_{v})^{k})}$

Para el modelo iterativo de refinamiento de variación total direccional, los multiplicadores lagrangianos se actualizan de la siguiente manera:

${\displaystyle (\lambda _{P})^{k}=(\lambda _{P})^{k-1}+\gamma _{P}P^{k}-\nabla (\mathrm {X} )^{k})}$

${\displaystyle (\lambda _{Q})^{k}=(\lambda _{Q})^{k-1}+\gamma _{Q}(Q^{k}-P^{k}\bullet d)}$

Aquí hay constantes positivas.${\displaystyle \gamma _{H},\gamma _{V},\gamma _{P},\gamma _{Q}}$

Con base en las métricas de relación señal-ruido (PSNR) y del índice de similitud estructural (SSIM) y en las imágenes de verdad de campo conocidas para probar el rendimiento, se concluye que la variación total direccional iterativa tiene un mejor rendimiento reconstruido que los métodos no iterativos en la preservación de las áreas de borde y textura. El modelo de refinamiento del campo de orientación desempeña un papel importante en esta mejora del rendimiento, ya que aumenta la cantidad de píxeles sin dirección en el área plana al tiempo que mejora la consistencia del campo de orientación en las regiones con bordes.

El campo de la detección compresiva está relacionado con varios temas en el procesamiento de señales y las matemáticas computacionales, como los sistemas lineales subdeterminados , las pruebas de grupo , los pesos pesados, la codificación dispersa , la multiplexación , el muestreo disperso y la tasa finita de innovación. Su amplio alcance y generalidad han permitido varios enfoques innovadores mejorados por CS en el procesamiento y la compresión de señales, la solución de problemas inversos, el diseño de sistemas radiantes, la obtención de imágenes por radar y a través de la pared, y la caracterización de antenas. ^[22] Las técnicas de obtención de imágenes que tienen una fuerte afinidad con la detección compresiva incluyen la apertura codificada y la fotografía computacional .

La reconstrucción CS convencional utiliza señales dispersas (generalmente muestreadas a una tasa menor que la tasa de muestreo de Nyquist) para la reconstrucción a través de la minimización restringida. Una de las primeras aplicaciones de este enfoque fue en la sismología de reflexión, que utilizó señales reflejadas dispersas de datos de banda limitada para rastrear cambios entre capas subterráneas. ^[23] Cuando el modelo LASSO adquirió importancia en la década de 1990 como un método estadístico para la selección de modelos dispersos, ^[24] este método se utilizó además en el análisis armónico computacional para la representación de señales dispersas a partir de diccionarios sobrecompletos. Algunas de las otras aplicaciones incluyen el muestreo incoherente de pulsos de radar. El trabajo de Boyd et al. ^[16] ha aplicado el modelo LASSO, para la selección de modelos dispersos, a los convertidores analógicos a digitales (los actuales utilizan una tasa de muestreo mayor que la tasa de Nyquist junto con la representación de Shannon cuantificada). Esto implicaría una arquitectura paralela en la que la polaridad de la señal analógica cambia a un ritmo elevado y luego se digitaliza la integral al final de cada intervalo de tiempo para obtener la señal digital convertida.${\displaystyle l_{1}}$

Se ha utilizado la detección comprimida en un sensor de cámara de teléfono móvil experimental. El enfoque permite una reducción de la energía de adquisición de imágenes por imagen en un factor de hasta 15 a costa de algoritmos de descompresión complejos; el cálculo puede requerir una implementación fuera del dispositivo. ^[25]

La detección comprimida se utiliza en cámaras de un solo píxel de la Universidad Rice . ^[26] Bell Labs empleó la técnica en una cámara de un solo píxel sin lente que toma fotografías utilizando instantáneas repetidas de aperturas elegidas al azar de una cuadrícula. La calidad de la imagen mejora con el número de instantáneas y, por lo general, requiere una pequeña fracción de los datos de las imágenes convencionales, al tiempo que elimina las aberraciones relacionadas con la lente y el enfoque. ^{[27] [28]}

La detección comprimida se puede utilizar para mejorar la reconstrucción de imágenes en holografía al aumentar la cantidad de vóxeles que se pueden inferir de un solo holograma. ^{[29] [30] [31]} También se utiliza para la recuperación de imágenes a partir de mediciones submuestreadas en holografía óptica ^{[32] [33]} y de ondas milimétricas ^{[34] .}

La detección comprimida se ha utilizado en aplicaciones de reconocimiento facial . ^[35]

La detección comprimida se ha utilizado ^{[36] [37]} para acortar las sesiones de exploración de imágenes por resonancia magnética en hardware convencional. ^[38] Los métodos de reconstrucción incluyen

• ISTA
• Primera vez
• Hermana
• ePRESS ^[39]
• EWISTA ^[40]
• EWISTARS ^[41] etc.

La detección comprimida resuelve el problema del alto tiempo de escaneo al permitir una adquisición más rápida al medir menos coeficientes de Fourier. Esto produce una imagen de alta calidad con un tiempo de escaneo relativamente menor. Otra aplicación (que también se analiza más adelante) es la reconstrucción de TC con menos proyecciones de rayos X. La detección comprimida, en este caso, elimina las partes de alto gradiente espacial, principalmente, el ruido y los artefactos de la imagen. Esto tiene un enorme potencial, ya que se pueden obtener imágenes de TC de alta resolución con dosis de radiación bajas (a través de configuraciones de corriente-mA más bajas). ^[42]

La detección comprimida ha mostrado resultados sobresalientes en la aplicación de la tomografía de red a la gestión de redes . La estimación del retraso de la red y la detección de la congestión de la red pueden modelarse como sistemas subdeterminados de ecuaciones lineales donde la matriz de coeficientes es la matriz de enrutamiento de la red. Además, en Internet , las matrices de enrutamiento de la red generalmente satisfacen el criterio para usar la detección comprimida. ^[43]

En 2013, una empresa anunció cámaras infrarrojas de onda corta que utilizan detección comprimida. ^[44] Estas cámaras tienen una sensibilidad a la luz de 0,9  μm a 1,7 μm, longitudes de onda invisibles para el ojo humano.

En radioastronomía e interferometría astronómica óptica , la cobertura total del plano de Fourier suele estar ausente y no se obtiene información de fase en la mayoría de las configuraciones de hardware. Para obtener imágenes de síntesis de apertura , se emplean varios algoritmos de detección comprimidos. ^[45] El algoritmo Högbom CLEAN se ha utilizado desde 1974 para la reconstrucción de imágenes obtenidas a partir de interferómetros de radio, que es similar al algoritmo de búsqueda coincidente mencionado anteriormente.

La detección comprimida combinada con una apertura móvil se ha utilizado para aumentar la velocidad de adquisición de imágenes en un microscopio electrónico de transmisión . ^[46] En el modo de escaneo , la detección comprimida combinada con el escaneo aleatorio del haz de electrones ha permitido una adquisición más rápida y una menor dosis de electrones, lo que permite obtener imágenes de materiales sensibles al haz de electrones. ^[47]

• Detección comprimida en señales de voz
• Código de comprobación de paridad de baja densidad
• Ruido
• Aproximación dispersa
• Codificación dispersa
• Algoritmos de transmisión de mensajes basados ​​en verificación en detección comprimida

• "Los fundamentos de la detección compresiva", parte 1, parte 2 y parte 3: video tutorial de Mark Davenport, Georgia Tech. en SigView, la biblioteca de tutoriales de la IEEE Signal Processing Society.
• Uso de las matemáticas para convertir conjuntos de datos de baja resolución en muestras de alta resolución Artículo de la revista Wired
• Recursos de detección de compresión en la Universidad Rice .
• La detección comprimida hace que cada píxel cuente: artículo de la serie Qué está pasando en las ciencias matemáticas de AMS
• Wiki sobre reconstrucción dispersa