Mínimos cuadrados ordinarios

En estadística , los mínimos cuadrados ordinarios ( MCO ) son un tipo de método de mínimos cuadrados lineales para elegir los parámetros desconocidos en un modelo de regresión lineal (con efectos de nivel uno fijos ^{[ aclaración necesaria ]} de una función lineal de un conjunto de variables explicativas ) mediante el principio de mínimos cuadrados : minimizar la suma de los cuadrados de las diferencias entre la variable dependiente observada (valores de la variable que se observa) en el conjunto de datos de entrada y la salida de la función (lineal) de la variable independiente . Algunas fuentes consideran que los MCO son una regresión lineal. ^[1]

Geométricamente, esto se ve como la suma de las distancias al cuadrado, paralelas al eje de la variable dependiente, entre cada punto de datos en el conjunto y el punto correspondiente en la superficie de regresión: cuanto menores sean las diferencias, mejor se ajusta el modelo a los datos. El estimador resultante se puede expresar mediante una fórmula simple, especialmente en el caso de una regresión lineal simple , en la que hay un solo regresor en el lado derecho de la ecuación de regresión.

El estimador MCO es consistente para los efectos fijos de nivel uno cuando los regresores son exógenos y forma una colinealidad perfecta (condición de rango), consistente para la estimación de la varianza de los residuos cuando los regresores tienen cuartos momentos finitos ^[2] y, por el teorema de Gauss-Markov , óptimo en la clase de estimadores lineales insesgados cuando los errores son homocedásticos y serialmente no correlacionados . Bajo estas condiciones, el método de MCO proporciona una estimación insesgada de media con varianza mínima cuando los errores tienen varianzas finitas . Bajo el supuesto adicional de que los errores se distribuyen normalmente con media cero, MCO es el estimador de máxima verosimilitud que supera a cualquier estimador insesgado no lineal.

Supongamos que los datos consisten en observaciones . Cada observación incluye una respuesta escalar y un vector columna de parámetros (regresores), es decir, . En un modelo de regresión lineal , la variable de respuesta, , es una función lineal de los regresores:${\displaystyle n}$ ${\displaystyle \left\{\mathbf {x} _{i},y_{i}\right\}_{i=1}^{n}}$${\displaystyle i}$${\displaystyle y_{i}}$${\displaystyle \mathbf {x} _{i}}$${\displaystyle p}$${\displaystyle \mathbf {x} _{i}=\left[x_{i1},x_{i2},\dots ,x_{ip}\right]^{\operatorname {T} }}$${\displaystyle y_{i}}$

${\displaystyle y_{i}=\beta _{1}\ x_{i1}+\beta _{2}\ x_{i2}+\cdots +\beta _{p}\ x_{ip}+\varepsilon _{i},}$

o en forma vectorial ,

${\displaystyle y_{i}=\mathbf {x} _{i}^{\operatorname {T} }{\boldsymbol {\beta }}+\varepsilon _{i},\,}$

donde , como se introdujo anteriormente, es un vector de columna de la -ésima observación de todas las variables explicativas; es un vector de parámetros desconocidos; y el escalar representa variables aleatorias no observadas ( errores ) de la -ésima observación. tiene en cuenta las influencias sobre las respuestas de fuentes distintas de las variables explicativas . Este modelo también se puede escribir en notación matricial como${\displaystyle \mathbf {x} _{i}}$${\displaystyle i}$${\displaystyle {\boldsymbol {\beta }}}$${\displaystyle p\times 1}$${\displaystyle \varepsilon _{i}}$${\displaystyle i}$${\displaystyle \varepsilon _{i}}$${\displaystyle y_{i}}$${\displaystyle \mathbf {x} _{i}}$

${\displaystyle \mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }},\,}$

donde y son vectores de las variables de respuesta y los errores de las observaciones, y es una matriz de regresores, también llamada a veces matriz de diseño , cuya fila es y contiene las -ésimas observaciones de todas las variables explicativas.${\displaystyle \mathbf {y} }$${\displaystyle {\boldsymbol {\varepsilon }}}$${\displaystyle n\times 1}$${\displaystyle n}$${\displaystyle \mathbf {X} }$${\displaystyle n\times p}$${\displaystyle i}$${\displaystyle \mathbf {x} _{i}^{\operatorname {T} }}$${\displaystyle i}$

Por lo general, se incluye un término constante en el conjunto de regresores , por ejemplo, tomando para todo . El coeficiente correspondiente a este regresor se denomina intersección . Sin la intersección, la línea ajustada se ve obligada a cruzar el origen cuando .${\displaystyle \mathbf {X} }$${\displaystyle x_{i1}=1}$${\displaystyle i=1,\dots ,n}$${\displaystyle \beta _{1}}$${\displaystyle x_{i}={\vec {0}}}$

Los regresores no tienen que ser independientes para que la estimación sea consistente, es decir, pueden ser no linealmente dependientes. A falta de una multicolinealidad perfecta, las estimaciones de los parámetros pueden seguir siendo consistentes; sin embargo, a medida que aumenta la multicolinealidad, el error estándar en torno a dichas estimaciones aumenta y reduce la precisión de dichas estimaciones. Cuando hay una multicolinealidad perfecta, ya no es posible obtener estimaciones únicas para los coeficientes de los regresores relacionados; la estimación de estos parámetros no puede converger (por lo tanto, no puede ser consistente).

Como ejemplo concreto en el que los regresores son dependientes de manera no lineal pero la estimación puede ser consistente, podríamos sospechar que la respuesta depende linealmente tanto de un valor como de su cuadrado; en cuyo caso incluiríamos un regresor cuyo valor es simplemente el cuadrado de otro regresor. En ese caso, el modelo sería cuadrático en el segundo regresor, pero aun así se lo considera un modelo lineal porque sigue siendo lineal en los parámetros ( ).${\displaystyle {\boldsymbol {\beta }}}$

Considere un sistema sobredeterminado

${\displaystyle \sum _{j=1}^{p}x_{ij}\beta _{j}=y_{i},\ (i=1,2,\dots ,n),}$

de ecuaciones lineales con coeficientes desconocidos , , con . Esto se puede escribir en forma matricial como${\displaystyle n}$ ${\displaystyle p}$${\displaystyle \beta _{1},\beta _{2},\dots ,\beta _{p}}$${\displaystyle n>p}$

${\displaystyle \mathbf {X} {\boldsymbol {\beta }}=\mathbf {y} ,}$

dónde

${\displaystyle \mathbf {X} ={\begin{bmatrix}X_{11}&X_{12}&\cdots &X_{1p}\\X_{21}&X_{22}&\cdots &X_{2p}\\\vdots &\vdots &\ddots &\vdots \\X_{n1}&X_{n2}&\cdots &X_{np}\end{bmatrix}},\qquad {\boldsymbol {\beta }}={\begin{bmatrix}\beta _{1}\\\beta _{2}\\\vdots \\\beta _{p}\end{bmatrix}},\qquad \mathbf {y} ={\begin{bmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{bmatrix}}.}$

(Nota: para un modelo lineal como el anterior, no todos los elementos contienen información sobre los puntos de datos. La primera columna se completa con unos, . Solo las otras columnas contienen datos reales. Por lo tanto, aquí es igual al número de regresores más uno).${\displaystyle \mathbf {X} }$${\displaystyle X_{i1}=1}$${\displaystyle p}$

Un sistema de este tipo normalmente no tiene una solución exacta, por lo que el objetivo es encontrar los coeficientes que se ajusten "mejor" a las ecuaciones, en el sentido de resolver el problema de minimización cuadrática .${\displaystyle {\boldsymbol {\beta }}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}={\underset {\boldsymbol {\beta }}{\operatorname {arg\,min} }}\,S({\boldsymbol {\beta }}),}$

donde la función objetivo está dada por${\displaystyle S}$

${\displaystyle S({\boldsymbol {\beta }})=\sum _{i=1}^{n}\left|y_{i}-\sum _{j=1}^{p}X_{ij}\beta _{j}\right|^{2}=\left\|\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}\right\|^{2}.}$

En Propiedades se ofrece una justificación para elegir este criterio. Este problema de minimización tiene una solución única, siempre que las columnas de la matriz sean linealmente independientes , que se obtiene resolviendo las denominadas ecuaciones normales :${\displaystyle p}$${\displaystyle \mathbf {X} }$

${\displaystyle \left(\mathbf {X} ^{\operatorname {T} }\mathbf {X} \right){\hat {\boldsymbol {\beta }}}=\mathbf {X} ^{\operatorname {T} }\mathbf {y} \ .}$

La matriz se conoce como matriz normal o matriz de Gram y la matriz se conoce como matriz de momento del regresando por regresores. ^[3] Finalmente, es el vector de coeficientes del hiperplano de mínimos cuadrados , expresado como${\displaystyle \mathbf {X} ^{\operatorname {T} }\mathbf {X} }$${\displaystyle \mathbf {X} ^{\operatorname {T} }\mathbf {y} }$${\displaystyle {\hat {\boldsymbol {\beta }}}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}=\left(\mathbf {X} ^{\operatorname {T} }\mathbf {X} \right)^{-1}\mathbf {X} ^{\operatorname {T} }\mathbf {y} .}$

o

${\displaystyle {\hat {\boldsymbol {\beta }}}={\boldsymbol {\beta }}+\left(\mathbf {X} ^{\operatorname {T} }\mathbf {X} \right)^{-1}\mathbf {X} ^{\operatorname {T} }{\boldsymbol {\varepsilon }}.}$

Supongamos que b es un valor "candidato" para el vector de parámetros β . La cantidad y _i − x _i ^T b , llamada residuo para la i -ésima observación, mide la distancia vertical entre el punto de datos ( x _i , y _i ) y el hiperplano y = x ^T b , y por lo tanto evalúa el grado de ajuste entre los datos reales y el modelo. La suma de los residuos al cuadrado ( SSR ) (también llamada suma de cuadrados del error ( ESS ) o suma de cuadrados de los residuos ( RSS )) ^[4] es una medida del ajuste general del modelo:

${\displaystyle S(b)=\sum _{i=1}^{n}(y_{i}-x_{i}^{\operatorname {T} }b)^{2}=(y-Xb)^{\operatorname {T} }(y-Xb),}$

donde T denota la matriz transpuesta , y las filas de X , que denotan los valores de todas las variables independientes asociadas con un valor particular de la variable dependiente, son X _i = x _i ^T . El valor de b que minimiza esta suma se llama estimador MCO para β . La función S ( b ) es cuadrática en b con hessiano definido positivo , y por lo tanto esta función posee un mínimo global único en , que puede darse por la fórmula explícita: ^{[5] [prueba]}${\displaystyle b={\hat {\beta }}}$

${\displaystyle {\hat {\beta }}=\operatorname {argmin} _{b\in \mathbb {R} ^{p}}S(b)=(X^{\operatorname {T} }X)^{-1}X^{\operatorname {T} }y\ .}$

El producto N = X ^T X es una matriz de Gram y su inversa, Q = N ^–1 , es la matriz de cofactores de β , ^{[6] [7] [8]} estrechamente relacionada con su matriz de covarianza, C _β . La matriz ( X ^T X ) ^–1 X ^T = Q X ^T se denomina matriz pseudoinversa de Moore-Penrose de X. Esta formulación resalta el punto de que la estimación se puede llevar a cabo si, y solo si, no hay multicolinealidad perfecta entre las variables explicativas (lo que causaría que la matriz de Gram no tuviera inversa).

Después de haber estimado β , los valores ajustados (o valores predichos ) de la regresión serán

${\displaystyle {\hat {y}}=X{\hat {\beta }}=Py,}$

donde P = X ( X ^T X ) ⁻¹ X ^T es la matriz de proyección sobre el espacio V abarcado por las columnas de X . Esta matriz P también se denomina a veces matriz del sombrero porque "pone un sombrero" sobre la variable y . Otra matriz, estrechamente relacionada con P es la matriz aniquiladora M = I _n − P ; esta es una matriz de proyección sobre el espacio ortogonal a V . Ambas matrices P y M son simétricas e idempotentes (lo que significa que P ² = P y M ² = M ), y se relacionan con la matriz de datos X a través de las identidades PX = X y MX = 0 . ^[9] La matriz M crea los residuos de la regresión:

${\displaystyle {\hat {\varepsilon }}=y-{\hat {y}}=y-X{\hat {\beta }}=My=M(X\beta +\varepsilon )=(MX)\beta +M\varepsilon =M\varepsilon .}$

Utilizando estos residuos podemos estimar el valor de σ ² utilizando la estadística chi-cuadrado reducida :

${\displaystyle s^{2}={\frac {{\hat {\varepsilon }}^{\mathrm {T} }{\hat {\varepsilon }}}{n-p}}={\frac {(My)^{\mathrm {T} }My}{n-p}}={\frac {y^{\mathrm {T} }M^{\mathrm {T} }My}{n-p}}={\frac {y^{\mathrm {T} }My}{n-p}}={\frac {S({\hat {\beta }})}{n-p}},\qquad {\hat {\sigma }}^{2}={\frac {n-p}{n}}\;s^{2}}$

El denominador, n − p , son los grados de libertad estadísticos . La primera cantidad, s ² , es la estimación de MCO para σ ² , mientras que la segunda, , es la estimación de MLE para σ ² . Los dos estimadores son bastante similares en muestras grandes; el primer estimador siempre es insesgado , mientras que el segundo estimador es sesgado pero tiene un error cuadrático medio menor . En la práctica, s ² se utiliza con más frecuencia, ya que es más conveniente para la prueba de hipótesis. La raíz cuadrada de s ² se denomina error estándar de regresión , ^[10] error estándar de la regresión , ^{[11] [12]} o error estándar de la ecuación . ^[9]${\displaystyle \scriptstyle {\hat {\sigma }}^{2}}$

Es común evaluar la bondad de ajuste de la regresión MCO comparando cuánto se puede reducir la variación inicial en la muestra al realizar una regresión sobre X. El coeficiente de determinación R ² se define como una relación entre la varianza "explicada" y la varianza "total" de la variable dependiente y , en los casos en que la suma de los cuadrados de la regresión es igual a la suma de los cuadrados de los residuos: ^[13]

${\displaystyle R^{2}={\frac {\sum ({\hat {y}}_{i}-{\overline {y}})^{2}}{\sum (y_{i}-{\overline {y}})^{2}}}={\frac {y^{\mathrm {T} }P^{\mathrm {T} }LPy}{y^{\mathrm {T} }Ly}}=1-{\frac {y^{\mathrm {T} }My}{y^{\mathrm {T} }Ly}}=1-{\frac {\rm {RSS}}{\rm {TSS}}}}$

donde TSS es la suma total de cuadrados para la variable dependiente, , y es una matriz n × n de unos. ( es una matriz de centrado que es equivalente a la regresión sobre una constante; simplemente resta la media de una variable). Para que R ² sea significativo, la matriz X de datos sobre regresores debe contener un vector columna de unos para representar la constante cuyo coeficiente es la intersección de la regresión. En ese caso, R ² siempre será un número entre 0 y 1, con valores cercanos a 1 indicando un buen grado de ajuste.${\textstyle L=I_{n}-{\frac {1}{n}}J_{n}}$${\textstyle J_{n}}$${\displaystyle L}$

La varianza en la predicción de la variable independiente en función de la variable dependiente se da en el artículo Mínimos cuadrados polinomiales .

Si la matriz de datos X contiene sólo dos variables, una constante y un regresor escalar x _i , entonces se denomina "modelo de regresión simple". Este caso se considera a menudo en las clases de estadística para principiantes, ya que proporciona fórmulas mucho más simples, incluso adecuadas para el cálculo manual. Los parámetros se denotan comúnmente como ( α , β ) :

${\displaystyle y_{i}=\alpha +\beta x_{i}+\varepsilon _{i}.}$

Las estimaciones de mínimos cuadrados en este caso se dan mediante fórmulas simples.

${\displaystyle {\begin{aligned}{\widehat {\beta }}&={\frac {\sum _{i=1}^{n}{(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}}{\sum _{i=1}^{n}{(x_{i}-{\bar {x}})^{2}}}}\\[2pt]{\widehat {\alpha }}&={\bar {y}}-{\widehat {\beta }}\,{\bar {x}}\ ,\end{aligned}}}$

En la sección anterior, el estimador de mínimos cuadrados se obtuvo como un valor que minimiza la suma de los cuadrados de los residuos del modelo. Sin embargo, también es posible obtener el mismo estimador a partir de otros enfoques. En todos los casos, la fórmula para el estimador de MCO sigue siendo la misma: ^{^} β = ( X ^T X ) ⁻¹ X ^T y ; la única diferencia está en cómo interpretamos este resultado.${\displaystyle {\hat {\beta }}}$

This section may need to be cleaned up. It has been merged from Linear least squares.

Para los matemáticos, MCO es una solución aproximada a un sistema sobredeterminado de ecuaciones lineales Xβ ≈ y , donde β es la incógnita. Suponiendo que el sistema no se puede resolver con exactitud (el número de ecuaciones n es mucho mayor que el número de incógnitas p ), buscamos una solución que pueda proporcionar la menor discrepancia entre los lados derecho e izquierdo. En otras palabras, buscamos la solución que satisfaga

${\displaystyle {\hat {\beta }}={\rm {arg}}\min _{\beta }\,\lVert \mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}\rVert ,}$

donde ‖ · ‖ es la  norma estándar L ² en el espacio euclidiano n -dimensional R ⁿ . La cantidad predicha Xβ es simplemente una cierta combinación lineal de los vectores de regresores. Por lo tanto, el vector residual y − Xβ tendrá la longitud más pequeña cuando y se proyecta ortogonalmente sobre el subespacio lineal abarcado por las columnas de X . El estimador MCO en este caso puede interpretarse como los coeficientes de descomposición vectorial de ^{^} y = Py a lo largo de la base de X . ${\displaystyle {\hat {\beta }}}$

En otras palabras, las ecuaciones de gradiente en el mínimo se pueden escribir como:

${\displaystyle (\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}})^{\top }\mathbf {X} =0.}$

Una interpretación geométrica de estas ecuaciones es que el vector de residuos, es ortogonal al espacio columna de X , ya que el producto escalar es igual a cero para cualquier vector conforme, v . Esto significa que es el más corto de todos los vectores posibles , es decir, la varianza de los residuos es la mínima posible. Esto se ilustra a la derecha.${\displaystyle \mathbf {y} -X{\hat {\boldsymbol {\beta }}}}$ ${\displaystyle (\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}})\cdot \mathbf {X} \mathbf {v} }$${\displaystyle \mathbf {y} -\mathbf {X} {\boldsymbol {\hat {\beta }}}}$${\displaystyle \mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}}$

Introduciendo una matriz K con el supuesto de que la matriz no es singular y K ^T X = 0 (cf. Proyecciones ortogonales ), el vector residual debe satisfacer la siguiente ecuación:${\displaystyle {\hat {\boldsymbol {\gamma }}}}$${\displaystyle [\mathbf {X} \ \mathbf {K} ]}$

${\displaystyle {\hat {\mathbf {r} }}:=\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}}=\mathbf {K} {\hat {\boldsymbol {\gamma }}}.}$

La ecuación y solución de mínimos cuadrados lineales se describen de la siguiente manera:

${\displaystyle {\begin{aligned}\mathbf {y} &={\begin{bmatrix}\mathbf {X} &\mathbf {K} \end{bmatrix}}{\begin{bmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {\gamma }}}\end{bmatrix}},\\{}\Rightarrow {\begin{bmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {\gamma }}}\end{bmatrix}}&={\begin{bmatrix}\mathbf {X} &\mathbf {K} \end{bmatrix}}^{-1}\mathbf {y} ={\begin{bmatrix}\left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }\\\left(\mathbf {K} ^{\top }\mathbf {K} \right)^{-1}\mathbf {K} ^{\top }\end{bmatrix}}\mathbf {y} .\end{aligned}}}$

Otra forma de verlo es considerar la línea de regresión como un promedio ponderado de las líneas que pasan por la combinación de dos puntos cualesquiera en el conjunto de datos. ^[14] Aunque esta forma de cálculo es computacionalmente más costosa, proporciona una mejor intuición sobre MCO.

El estimador MCO es idéntico al estimador de máxima verosimilitud (MLE) bajo el supuesto de normalidad para los términos de error. ^{[15] [prueba]} Este supuesto de normalidad tiene importancia histórica, ya que proporcionó la base para el trabajo temprano en análisis de regresión lineal de Yule y Pearson . ^{[ cita requerida ]} A partir de las propiedades del MLE, podemos inferir que el estimador MCO es asintóticamente eficiente (en el sentido de alcanzar el límite de Cramér-Rao para la varianza) si se satisface el supuesto de normalidad. ^[16]

En el caso iid , el estimador MCO también puede verse como un estimador GMM que surge de las condiciones del momento.

${\displaystyle \mathrm {E} {\big [}\,x_{i}\left(y_{i}-x_{i}^{\operatorname {T} }\beta \right)\,{\big ]}=0.}$

Estas condiciones de momento establecen que los regresores no deben estar correlacionados con los errores. Dado que x _i es un vector p , el número de condiciones de momento es igual a la dimensión del vector de parámetros β y, por lo tanto, el sistema se identifica exactamente. Este es el llamado caso GMM clásico, cuando el estimador no depende de la elección de la matriz de ponderación.

Obsérvese que el supuesto original de exogeneidad estricta E[ ε _i  |  x _i ] = 0 implica un conjunto mucho más rico de condiciones de momento que el indicado anteriormente. En particular, este supuesto implica que para cualquier función vectorial ƒ , se cumplirá la condición de momento E[ ƒ ( x _i )· ε _i ] = 0. Sin embargo, se puede demostrar utilizando el teorema de Gauss-Markov que la elección óptima de la función ƒ es tomar ƒ ( x ) = x , lo que da como resultado la ecuación de momento publicada anteriormente.

Existen varios marcos diferentes en los que se puede aplicar el modelo de regresión lineal para que la técnica MCO sea aplicable. Cada uno de estos marcos produce las mismas fórmulas y los mismos resultados. La única diferencia es la interpretación y los supuestos que se deben imponer para que el método proporcione resultados significativos. La elección del marco aplicable depende principalmente de la naturaleza de los datos disponibles y de la tarea de inferencia que se debe realizar.

Una de las líneas de diferencia en la interpretación es si se deben tratar los regresores como variables aleatorias o como constantes predefinidas. En el primer caso ( diseño aleatorio ), los regresores x _i son aleatorios y se muestrean junto con los y _i de alguna población , como en un estudio observacional . Este enfoque permite un estudio más natural de las propiedades asintóticas de los estimadores. En la otra interpretación ( diseño fijo ), los regresores X se tratan como constantes conocidas establecidas por un diseño , y y se muestrea condicionalmente en los valores de X como en un experimento . Para fines prácticos, esta distinción a menudo no es importante, ya que la estimación y la inferencia se llevan a cabo mientras se condiciona a X. Todos los resultados indicados en este artículo están dentro del marco del diseño aleatorio.

El modelo clásico se centra en la estimación e inferencia de "muestras finitas", es decir, que el número de observaciones n es fijo. Esto contrasta con los otros enfoques, que estudian el comportamiento asintótico de MCO, y en los que se estudia el comportamiento en un gran número de muestras.

• Especificación correcta . La forma funcional lineal debe coincidir con la forma del proceso real de generación de datos.
• Exogeneidad estricta . Los errores en la regresión deben tener media condicional cero: ^[17] La ​​consecuencia inmediata del supuesto de exogeneidad es que los errores tienen media cero: E[ ε ] = 0 (para la ley de expectativa total ), y que los regresores no están correlacionados con los errores: E[ X ^T ε ] = 0 .$${\displaystyle \operatorname {E} [\,\varepsilon \mid X\,]=0.}$$
  El supuesto de exogeneidad es fundamental para la teoría de MCO. Si se cumple, las variables regresoras se denominan exógenas . Si no, los regresores que están correlacionados con el término de error se denominan endógenos ^[18] y el estimador de MCO se vuelve sesgado. En tal caso, se puede utilizar el método de variables instrumentales para realizar inferencias.
• No hay dependencia lineal . Los regresores en X deben ser todos linealmente independientes . Matemáticamente, esto significa que la matriz X debe tener rango de columna completo casi con seguridad: ^[19] Por lo general, también se supone que los regresores tienen momentos finitos hasta al menos el segundo momento. Entonces la matriz Q _xx = E[ X ^T X  /  n ] es finita y semidefinida positiva.$${\displaystyle \Pr \!{\big [}\,\operatorname {rank} (X)=p\,{\big ]}=1.}$$
  Cuando se viola este supuesto, los regresores se denominan linealmente dependientes o perfectamente multicolineales . En tal caso, no se puede aprender el valor del coeficiente de regresión β , aunque todavía es posible predecir los valores y para nuevos valores de los regresores que se encuentran en el mismo subespacio linealmente dependiente.
• Errores esféricos : ^[19] donde I _n es la matriz identidad en dimensión n , y σ ² es un parámetro que determina la varianza de cada observación. Este σ ² se considera un parámetro molesto en el modelo, aunque normalmente también se estima. Si se viola este supuesto, las estimaciones MCO siguen siendo válidas, pero ya no son eficientes.$${\displaystyle \operatorname {Var} [\,\varepsilon \mid X\,]=\sigma ^{2}I_{n},}$$
  Se suele dividir esta suposición en dos partes:
  • Homocedasticidad : E[  ε _i ²  |  X  ] = σ ² , lo que significa que el término de error tiene la misma varianza σ ² en cada observación. Cuando se viola este requisito se denomina heterocedasticidad ; en ese caso, un estimador más eficiente sería el de mínimos cuadrados ponderados . Si los errores tienen varianza infinita, las estimaciones MCO también tendrán varianza infinita (aunque, por la ley de los grandes números, tenderán de todos modos hacia los valores verdaderos siempre que los errores tengan media cero). En este caso,se recomiendan técnicas de estimación robustas .
  • Sin autocorrelación : los errores no están correlacionados entre las observaciones: E[  ε _i ε _j  |  X  ] = 0 para i ≠ j . Esta suposición puede violarse en el contexto de datos de series temporales , datos de panel , muestras de conglomerados, datos jerárquicos, datos de medidas repetidas, datos longitudinales y otros datos con dependencias. En tales casos, los mínimos cuadrados generalizados proporcionan una mejor alternativa que los MCO. Otra expresión para la autocorrelación es la correlación serial .
• Normalidad . A veces se supone además que los errores tienen una distribución normal condicional a los regresores: ^[20] Esta suposición no es necesaria para la validez del método MCO, aunque se pueden establecer ciertas propiedades adicionales de muestra finita en caso de que así sea (especialmente en el área de prueba de hipótesis). Además, cuando los errores son normales, el estimador MCO es equivalente al estimador de máxima verosimilitud (EMV) y, por lo tanto, es asintóticamente eficiente en la clase de todos los estimadores regulares . Es importante destacar que la suposición de normalidad se aplica solo a los términos de error; contrariamente a un error común, no se requiere que la variable de respuesta (dependiente) tenga una distribución normal. ^[21]$${\displaystyle \varepsilon \mid X\sim {\mathcal {N}}(0,\sigma ^{2}I_{n}).}$$

En algunas aplicaciones, especialmente con datos transversales , se impone un supuesto adicional: que todas las observaciones son independientes y se distribuyen de manera idéntica . Esto significa que todas las observaciones se toman de una muestra aleatoria , lo que hace que todos los supuestos enumerados anteriormente sean más simples y fáciles de interpretar. Además, este marco permite establecer resultados asintóticos (como el tamaño de la muestra n  → ∞ ), que se entienden como una posibilidad teórica de obtener nuevas observaciones independientes del proceso de generación de datos . La lista de supuestos en este caso es:

• Observaciones iid : ( x _i , y _i ) es independiente y tiene la misma distribución que ( x _j , y _j ) para todo i ≠ j ;
• no hay multicolinealidad perfecta : Q _xx = E[  x _i  x _i ^T  ] es una matriz definida positiva ;
• exogeneidad : E[  ε _i  |  x _i  ] = 0;
• homocedasticidad : Var[  ε _i  |  x _i  ] = σ ² .

• El proceso estocástico { x _i , y _i } es estacionario y ergódico ; si { x _i , y _i } no es estacionario, los resultados MCO suelen ser espurios a menos que { x _i , y _i } sea cointegrante . ^[22]
• Los regresores están predeterminados : E[ x _i ε _i ] = 0 para todo i = 1, ..., n ;
• La matriz p × p Q _xx = E[  x _i  x _i ^T  ] es de rango completo y, por lo tanto, definida positiva ;
• { x _i ε _i } es una secuencia de diferencias de martingala , con una matriz finita de segundos momentos Q _{xxε ²} = E[  ε _i ² x _i  x _i ^T  ] .

En primer lugar, bajo el estricto supuesto de exogeneidad, los estimadores MCO y s ² son insesgados , lo que significa que sus valores esperados coinciden con los valores verdaderos de los parámetros: ^{[23] [prueba]}${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {E} [\,{\hat {\beta }}\mid X\,]=\beta ,\quad \operatorname {E} [\,s^{2}\mid X\,]=\sigma ^{2}.}$

Si la exogeneidad estricta no se cumple (como es el caso de muchos modelos de series de tiempo , donde la exogeneidad se supone solo con respecto a los shocks pasados ​​pero no a los futuros), entonces estos estimadores estarán sesgados en muestras finitas.

La matriz de varianza-covarianza (o simplemente matriz de covarianza ) de es igual a ^[24]${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {Var} [\,{\hat {\beta }}\mid X\,]=\sigma ^{2}\left(X^{\operatorname {T} }X\right)^{-1}=\sigma ^{2}Q.}$

En particular, el error estándar de cada coeficiente es igual a la raíz cuadrada del j -ésimo elemento diagonal de esta matriz. La estimación de este error estándar se obtiene reemplazando la cantidad desconocida σ ² por su estimación s ² . Por lo tanto,${\displaystyle \scriptstyle {\hat {\beta }}_{j}}$

${\displaystyle {\widehat {\operatorname {s.\!e.} }}({\hat {\beta }}_{j})={\sqrt {s^{2}\left(X^{\operatorname {T} }X\right)_{jj}^{-1}}}}$

También se puede demostrar fácilmente que el estimador no está correlacionado con los residuos del modelo: ^[24]${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {Cov} [\,{\hat {\beta }},{\hat {\varepsilon }}\mid X\,]=0.}$

El teorema de Gauss-Markov establece que, bajo el supuesto de errores esféricos (es decir, los errores deben ser no correlacionados y homocedásticos ), el estimador es eficiente en la clase de estimadores lineales insesgados. Esto se denomina el mejor estimador lineal insesgado (BLUE). La eficiencia debe entenderse como si tuviéramos que encontrar otro estimador que fuera lineal en y e insesgado, entonces ^[24]${\displaystyle \scriptstyle {\hat {\beta }}}$${\displaystyle \scriptstyle {\tilde {\beta }}}$

${\displaystyle \operatorname {Var} [\,{\tilde {\beta }}\mid X\,]-\operatorname {Var} [\,{\hat {\beta }}\mid X\,]\geq 0}$

en el sentido de que se trata de una matriz definida no negativa . Este teorema establece la optimalidad solo en la clase de estimadores lineales insesgados, lo que es bastante restrictivo. Dependiendo de la distribución de los términos de error ε , otros estimadores no lineales pueden proporcionar mejores resultados que MCO.

Las propiedades enumeradas hasta ahora son todas válidas independientemente de la distribución subyacente de los términos de error. Sin embargo, si está dispuesto a asumir que se cumple el supuesto de normalidad (es decir, que ε ~ N (0, σ ² I _n ) ), entonces se pueden indicar propiedades adicionales de los estimadores MCO.

El estimador se distribuye normalmente, con media y varianza como las indicadas anteriormente: ^[25]${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle {\hat {\beta }}\ \sim \ {\mathcal {N}}{\big (}\beta ,\ \sigma ^{2}(X^{\mathrm {T} }X)^{-1}{\big )}.}$

Este estimador alcanza el límite de Cramér-Rao para el modelo y, por lo tanto, es óptimo en la clase de todos los estimadores insesgados. ^[16] Nótese que, a diferencia del teorema de Gauss-Markov , este resultado establece la optimalidad entre los estimadores lineales y no lineales, pero solo en el caso de términos de error distribuidos normalmente.

El estimador s ² será proporcional a la distribución chi-cuadrado : ^[26]

${\displaystyle s^{2}\ \sim \ {\frac {\sigma ^{2}}{n-p}}\cdot \chi _{n-p}^{2}}$

La varianza de este estimador es igual a 2 σ ⁴ /( n  −  p ) , que no alcanza el límite de Cramér–Rao de 2 σ ⁴ / n . Sin embargo, se demostró que no hay estimadores insesgados de σ ² con varianza menor que la del estimador s ² . ^[27] Si estamos dispuestos a permitir estimadores sesgados y consideramos la clase de estimadores que son proporcionales a la suma de los residuos al cuadrado (SSR) del modelo, entonces el mejor estimador (en el sentido del error cuadrático medio ) en esta clase será ^~ σ ² = SSR  /  ( n  −  p  + 2) , que incluso supera el límite de Cramér–Rao en el caso en que solo haya un regresor ( p = 1 ). ^[28]

Además, los estimadores y s ² son independientes , ^[29] hecho que resulta útil al construir las pruebas t y F para la regresión.${\displaystyle \scriptstyle {\hat {\beta }}}$

Como se mencionó anteriormente, el estimador es lineal en y , lo que significa que representa una combinación lineal de las variables dependientes y _i . Los pesos en esta combinación lineal son funciones de los regresores X , y generalmente son desiguales. Las observaciones con pesos altos se denominan influyentes porque tienen un efecto más pronunciado en el valor del estimador.${\displaystyle {\hat {\beta }}}$

Para analizar qué observaciones son influyentes, eliminamos una observación j -ésima específica y consideramos cuánto van a cambiar las cantidades estimadas (de manera similar al método jackknife ). Se puede demostrar que el cambio en el estimador MCO para β será igual a ^[30]

${\displaystyle {\hat {\beta }}^{(j)}-{\hat {\beta }}=-{\frac {1}{1-h_{j}}}(X^{\mathrm {T} }X)^{-1}x_{j}^{\mathrm {T} }{\hat {\varepsilon }}_{j}\,,}$

donde h _j = x _j ^T  ( X ^T X ) ⁻¹ x _j es el j -ésimo elemento diagonal de la matriz de sombrero P , y x _j es el vector de regresores correspondiente a la j -ésima observación. De manera similar, el cambio en el valor predicho para la j -ésima observación resultante de omitir esa observación del conjunto de datos será igual a ^[30]

${\displaystyle {\hat {y}}_{j}^{(j)}-{\hat {y}}_{j}=x_{j}^{\mathrm {T} }{\hat {\beta }}^{(j)}-x_{j}^{\operatorname {T} }{\hat {\beta }}=-{\frac {h_{j}}{1-h_{j}}}\,{\hat {\varepsilon }}_{j}}$

De las propiedades de la matriz de sombrero, 0 ≤ h _j ≤ 1 , y suman p , de modo que en promedio h _j ≈ p/n . Estas cantidades h _j se denominan apalancamientos , y las observaciones con h _j alto se denominan puntos de apalancamiento . ^[31] Por lo general, las observaciones con alto apalancamiento deben examinarse con más cuidado, en caso de que sean erróneas, o valores atípicos, o de alguna otra manera atípicas del resto del conjunto de datos.

A veces, las variables y los parámetros correspondientes en la regresión se pueden dividir lógicamente en dos grupos, de modo que la regresión tome la forma

${\displaystyle y=X_{1}\beta _{1}+X_{2}\beta _{2}+\varepsilon ,}$

donde X ₁ y X ₂ tienen dimensiones n × p ₁ , n × p ₂ , y β ₁ , β ₂ son vectores p ₁ ×1 y p ₂ ×1, con p ₁ + p ₂ = p .

El teorema de Frisch–Waugh–Lovell establece que en esta regresión los residuos y la estimación de MCO serán numéricamente idénticos a los residuos y la estimación de MCO para β ₂ en la siguiente regresión: ^[32]${\displaystyle {\hat {\varepsilon }}}$${\displaystyle \scriptstyle {\hat {\beta }}_{2}}$

${\displaystyle M_{1}y=M_{1}X_{2}\beta _{2}+\eta \,,}$

donde M ₁ es la matriz aniquiladora para los regresores X ₁ .

El teorema se puede utilizar para establecer una serie de resultados teóricos. Por ejemplo, tener una regresión con una constante y otro regresor es equivalente a restar las medias de la variable dependiente y del regresor y luego ejecutar la regresión para las variables desmediadas pero sin el término constante.

Supongamos que se sabe que los coeficientes de la regresión satisfacen un sistema de ecuaciones lineales.

${\displaystyle A\colon \quad Q^{\operatorname {T} }\beta =c,\,}$

donde Q es una matriz p × q de rango completo, y c es un vector q ×1 de constantes conocidas, donde q < p . En este caso, la estimación por mínimos cuadrados es equivalente a minimizar la suma de los residuos cuadrados del modelo sujeto a la restricción A . El estimador de mínimos cuadrados restringidos (CLS) puede darse mediante una fórmula explícita: ^[33]

${\displaystyle {\hat {\beta }}^{c}={\hat {\beta }}-(X^{\operatorname {T} }X)^{-1}Q{\Big (}Q^{\operatorname {T} }(X^{\operatorname {T} }X)^{-1}Q{\Big )}^{-1}(Q^{\operatorname {T} }{\hat {\beta }}-c).}$

Esta expresión para el estimador restringido es válida siempre que la matriz X ^T X sea invertible. Se asumió desde el comienzo de este artículo que esta matriz es de rango completo, y se observó que cuando la condición de rango falla, β no será identificable. Sin embargo, puede suceder que al agregar la restricción A se haga que β sea identificable, en cuyo caso sería conveniente encontrar la fórmula para el estimador. El estimador es igual a ^[34]

${\displaystyle {\hat {\beta }}^{c}=R(R^{\operatorname {T} }X^{\operatorname {T} }XR)^{-1}R^{\operatorname {T} }X^{\operatorname {T} }y+{\Big (}I_{p}-R(R^{\operatorname {T} }X^{\operatorname {T} }XR)^{-1}R^{\operatorname {T} }X^{\operatorname {T} }X{\Big )}Q(Q^{\operatorname {T} }Q)^{-1}c,}$

donde R es una matriz p ×( p  −  q ) tal que la matriz [ QR ] no es singular, y R ^T Q = 0 . Siempre se puede encontrar una matriz de este tipo, aunque generalmente no es única. La segunda fórmula coincide con la primera en el caso en que X ^T X sea invertible. ^[34]

Los estimadores de mínimos cuadrados son estimaciones puntuales de los parámetros del modelo de regresión lineal β . Sin embargo, generalmente también queremos saber qué tan cerca pueden estar esas estimaciones de los valores verdaderos de los parámetros. En otras palabras, queremos construir las estimaciones de intervalo .

Dado que no hemos hecho ninguna suposición sobre la distribución del término de error ε _i , es imposible inferir la distribución de los estimadores y . No obstante, podemos aplicar el teorema del límite central para derivar sus propiedades asintóticas a medida que el tamaño de la muestra n tiende al infinito. Si bien el tamaño de la muestra es necesariamente finito, se acostumbra suponer que n es "lo suficientemente grande" para que la distribución verdadera del estimador MCO esté cerca de su límite asintótico.${\displaystyle {\hat {\beta }}}$${\displaystyle {\hat {\sigma }}^{2}}$

Podemos demostrar que, bajo los supuestos del modelo, el estimador de mínimos cuadrados para β es consistente (es decir, converge en probabilidad a β ) y asintóticamente normal: ^[prueba]${\displaystyle {\hat {\beta }}}$

${\displaystyle ({\hat {\beta }}-\beta )\ {\xrightarrow {d}}\ {\mathcal {N}}{\big (}0,\;\sigma ^{2}Q_{xx}^{-1}{\big )},}$

dónde${\displaystyle Q_{xx}=X^{\operatorname {T} }X.}$

Utilizando esta distribución asintótica, se pueden construir intervalos de confianza bilaterales aproximados para el componente j -ésimo del vector como${\displaystyle {\hat {\beta }}}$

${\displaystyle \beta _{j}\in {\bigg [}\ {\hat {\beta }}_{j}\pm q_{1-{\frac {\alpha }{2}}}^{{\mathcal {N}}(0,1)}\!{\sqrt {{\hat {\sigma }}^{2}\left[Q_{xx}^{-1}\right]_{jj}}}\ {\bigg ]}}$   en el nivel de confianza 1 −  α ,

donde q denota la función cuantil de una distribución normal estándar, y [·] _jj es el j -ésimo elemento diagonal de una matriz.

De manera similar, el estimador de mínimos cuadrados para σ ² también es consistente y asintóticamente normal (siempre que exista el cuarto momento de ε _i ) con una distribución límite

${\displaystyle ({\hat {\sigma }}^{2}-\sigma ^{2})\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\operatorname {E} \left[\varepsilon _{i}^{4}\right]-\sigma ^{4}\right).}$

Estas distribuciones asintóticas se pueden utilizar para la predicción, la comprobación de hipótesis, la construcción de otros estimadores, etc. Como ejemplo, considere el problema de la predicción. Suponga que hay un punto dentro del dominio de distribución de los regresores y se desea saber cuál habría sido la variable de respuesta en ese punto. La respuesta media es la cantidad , mientras que la respuesta predicha es . Claramente, la respuesta predicha es una variable aleatoria, su distribución se puede derivar de la de :${\displaystyle x_{0}}$${\displaystyle y_{0}=x_{0}^{\mathrm {T} }\beta }$${\displaystyle {\hat {y}}_{0}=x_{0}^{\mathrm {T} }{\hat {\beta }}}$${\displaystyle {\hat {\beta }}}$

${\displaystyle \left({\hat {y}}_{0}-y_{0}\right)\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\sigma ^{2}x_{0}^{\mathrm {T} }Q_{xx}^{-1}x_{0}\right),}$

que permite construir intervalos de confianza para la respuesta media :${\displaystyle y_{0}}$

${\displaystyle y_{0}\in \left[\ x_{0}^{\mathrm {T} }{\hat {\beta }}\pm q_{1-{\frac {\alpha }{2}}}^{{\mathcal {N}}(0,1)}\!{\sqrt {{\hat {\sigma }}^{2}x_{0}^{\mathrm {T} }Q_{xx}^{-1}x_{0}}}\ \right]}$   en el nivel de confianza 1 −  α .

This section needs expansion. You can help by adding to it. (February 2017)

Se utilizan con mucha frecuencia dos pruebas de hipótesis. En primer lugar, se quiere saber si la ecuación de regresión estimada es mejor que simplemente predecir que todos los valores de la variable de respuesta son iguales a su media muestral (si no, se dice que no tiene poder explicativo). La hipótesis nula de que la regresión estimada no tiene valor explicativo se prueba utilizando una prueba F. Si se encuentra que el valor F calculado es lo suficientemente grande como para superar su valor crítico para el nivel de significancia preseleccionado, se rechaza la hipótesis nula y se acepta la hipótesis alternativa de que la regresión tiene poder explicativo. De lo contrario, se acepta la hipótesis nula de que no tiene poder explicativo.

En segundo lugar, para cada variable explicativa de interés, se desea saber si su coeficiente estimado difiere significativamente de cero, es decir, si esta variable explicativa en particular tiene de hecho poder explicativo para predecir la variable de respuesta. Aquí la hipótesis nula es que el coeficiente verdadero es cero. Esta hipótesis se prueba calculando el estadístico t del coeficiente , como la relación entre la estimación del coeficiente y su error estándar . Si el estadístico t es mayor que un valor predeterminado, se rechaza la hipótesis nula y se determina que la variable tiene poder explicativo, con un coeficiente significativamente diferente de cero. De lo contrario, se acepta la hipótesis nula de un valor cero del coeficiente verdadero.

Además, se utiliza la prueba de Chow para comprobar si dos submuestras tienen los mismos valores de coeficientes reales subyacentes. La suma de los cuadrados de los residuos de las regresiones en cada uno de los subconjuntos y en el conjunto de datos combinados se compara calculando una estadística F; si esta supera un valor crítico, se rechaza la hipótesis nula de que no hay diferencias entre los dos subconjuntos; de lo contrario, se acepta.

El siguiente conjunto de datos proporciona las alturas y pesos promedio de las mujeres estadounidenses de 30 a 39 años (fuente: The World Almanac and Book of Facts, 1975 ).

Altura (m)	1.47	1,50	1.52	1,55	1.57
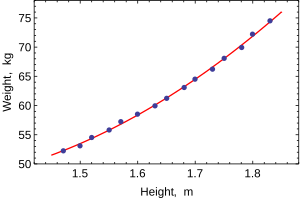
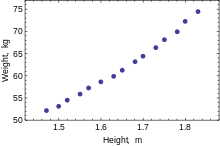
Peso (kg)	52.21	53.12	54,48	55,84	57,20
Altura (m)	1.60	1.63	1,65	1.68	1,70
Peso (kg)	58,57	59,93	61,29	63.11	64,47
Altura (m)	1,73	1,75	1,78	1,80	1.83
Peso (kg)	66,28	68.10	69,92	72,19	74,46

Cuando se modela una sola variable dependiente, un diagrama de dispersión sugerirá la forma y la fuerza de la relación entre la variable dependiente y los regresores. También podría revelar valores atípicos, heterocedasticidad y otros aspectos de los datos que pueden complicar la interpretación de un modelo de regresión ajustado. El diagrama de dispersión sugiere que la relación es fuerte y se puede aproximar como una función cuadrática. MCO puede manejar relaciones no lineales al introducir el regresor HEIGHT ² . El modelo de regresión se convierte entonces en un modelo lineal múltiple:

${\displaystyle w_{i}=\beta _{1}+\beta _{2}h_{i}+\beta _{3}h_{i}^{2}+\varepsilon _{i}.}$

La salida de los paquetes estadísticos más populares se verá similar a esto:

Método	Mínimos cuadrados
Variable dependiente	PESO
Observaciones	15
Parámetro	Valor	Error estándar	estadística t	valor p
${\displaystyle \beta _{1}}$	128.8128	16.3083	7.8986	0.0000
${\displaystyle \beta _{2}}$	–143,1620	19.8332	–7,2183	0.0000
${\displaystyle \beta _{3}}$	61.9603	6.0084	10.3122	0.0000
R2​	0,9989	SE de regresión		0,2516
R2 ajustado	0,9987	Modelo suma de cuadrados.		692.61
Log-verosimilitud	1.0890	Suma de cuadrados residuales.		0,7595
Estadística de Durbin–Watson.	2.1013	Suma total de cuadrados.		693.37
Criterio de Akaike	0,2548	Estadística F		5471.2
Criterio de Schwarz	0,3964	Valor p (estadística F)		0.0000

En esta tabla:

• La columna Valor proporciona las estimaciones de mínimos cuadrados de los parámetros β _j
• La columna de error estándar muestra los errores estándar de cada estimación de coeficiente:${\displaystyle {\hat {\sigma }}_{j}=\left({\hat {\sigma }}^{2}\left[Q_{xx}^{-1}\right]_{jj}\right)^{\frac {1}{2}}}$
• Las columnas de estadística t y valor p prueban si alguno de los coeficientes podría ser igual a cero. La estadística t se calcula simplemente como . Si los errores ε siguen una distribución normal, t sigue una distribución t de Student. En condiciones más débiles, t es asintóticamente normal. Los valores grandes de t indican que la hipótesis nula puede rechazarse y que el coeficiente correspondiente no es cero. La segunda columna, valor p , expresa los resultados de la prueba de hipótesis como un nivel de significancia . Convencionalmente, los valores p menores de 0,05 se toman como evidencia de que el coeficiente de población es distinto de cero.${\displaystyle t={\hat {\beta }}_{j}/{\hat {\sigma }}_{j}}$
• R-cuadrado es el coeficiente de determinación que indica la bondad de ajuste de la regresión. Esta estadística será igual a uno si el ajuste es perfecto y a cero cuando los regresores X no tengan poder explicativo alguno. Esta es una estimación sesgada del R-cuadrado de la población y nunca disminuirá si se agregan regresores adicionales, incluso si son irrelevantes.
• El R cuadrado ajustado es una versión ligeramente modificada de , diseñada para penalizar el exceso de número de regresores que no aumentan el poder explicativo de la regresión. Esta estadística siempre es menor que , puede disminuir a medida que se agregan nuevos regresores e incluso puede ser negativa para modelos con un ajuste deficiente:${\displaystyle R^{2}}$${\displaystyle R^{2}}$

${\displaystyle {\overline {R}}^{2}=1-{\frac {n-1}{n-p}}(1-R^{2})}$

• La verosimilitud logarítmica se calcula suponiendo que los errores siguen una distribución normal. Aunque esta suposición no es muy razonable, esta estadística puede resultar útil para realizar pruebas de probabilidad logarítmica.
• La estadística de Durbin-Watson prueba si existe alguna evidencia de correlación serial entre los residuos. Como regla general, un valor menor a 2 será evidencia de correlación positiva.
• Tanto el criterio de información de Akaike como el criterio de Schwarz se utilizan para la selección de modelos. Generalmente, cuando se comparan dos modelos alternativos, los valores más bajos de uno de estos criterios indicarán un modelo mejor. ^[35]
• El error estándar de regresión es una estimación de σ , el error estándar del término de error.
• La suma total de cuadrados , la suma de cuadrados del modelo y la suma de cuadrados residuales nos indican qué parte de la variación inicial en la muestra se explicó mediante la regresión.
• El estadístico F intenta probar la hipótesis de que todos los coeficientes (excepto el intercepto) son iguales a cero. Este estadístico tiene una distribución F ( p–1 , n–p ) bajo la hipótesis nula y el supuesto de normalidad, y su valor p indica la probabilidad de que la hipótesis sea verdadera. Tenga en cuenta que cuando los errores no son normales, este estadístico deja de ser válido y se deben utilizar otras pruebas, como la prueba de Wald o la prueba LR .

El análisis de mínimos cuadrados ordinarios suele incluir el uso de gráficos de diagnóstico diseñados para detectar desviaciones de los datos con respecto a la forma asumida del modelo. Estos son algunos de los gráficos de diagnóstico más comunes:

• Residuos en relación con las variables explicativas del modelo. Una relación no lineal entre estas variables sugiere que la linealidad de la función de media condicional puede no ser válida. Los diferentes niveles de variabilidad en los residuos para los distintos niveles de las variables explicativas sugieren una posible heterocedasticidad.
• Residuos frente a variables explicativas que no están en el modelo. Cualquier relación de los residuos con estas variables sugeriría considerar su inclusión en el modelo.
• Residuos frente a los valores ajustados, .${\displaystyle {\hat {y}}}$
• Residuos en relación con el residuo anterior. Este gráfico puede identificar correlaciones seriales en los residuos.

Una consideración importante al realizar inferencias estadísticas mediante modelos de regresión es cómo se muestrearon los datos. En este ejemplo, los datos son promedios en lugar de mediciones de mujeres individuales. El ajuste del modelo es muy bueno, pero esto no implica que el peso de una mujer individual pueda predecirse con alta precisión basándose únicamente en su altura.

Este ejemplo también demuestra que los coeficientes determinados por estos cálculos son sensibles a la forma en que se preparan los datos. Las alturas se dieron originalmente redondeadas a la pulgada más cercana y se han convertido y redondeado al centímetro más cercano. Dado que el factor de conversión es una pulgada por 2,54 cm, esta no es una conversión exacta. Las pulgadas originales se pueden recuperar con Round(x/0.0254) y luego se pueden convertir nuevamente al sistema métrico sin redondear. Si se hace esto, los resultados serán:

Si se utiliza cualquiera de estas ecuaciones para predecir el peso de una mujer de 1,6764 m (5' 6"), se obtienen valores similares: 62,94 kg con redondeo frente a 62,98 kg sin redondeo. Por lo tanto, una variación aparentemente pequeña en los datos tiene un efecto real en los coeficientes, pero un efecto pequeño en los resultados de la ecuación.

Si bien esto puede parecer inocuo en el medio del rango de datos, podría volverse significativo en los extremos o en el caso en que el modelo ajustado se use para proyectar fuera del rango de datos ( extrapolación ).

Esto pone de relieve un error común: este ejemplo es un abuso de MCO, que inherentemente requiere que los errores en la variable independiente (en este caso la altura) sean cero o al menos insignificantes. El redondeo inicial a la pulgada más cercana más cualquier error de medición real constituye un error finito y no insignificante. Como resultado, los parámetros ajustados no son las mejores estimaciones que se supone que son. Aunque no es totalmente espurio, el error en la estimación dependerá del tamaño relativo de los errores x e y .

Podemos utilizar el mecanismo de mínimos cuadrados para calcular la ecuación de una órbita de dos cuerpos en coordenadas de base polar. La ecuación que se utiliza normalmente es donde es el radio de la distancia entre el objeto y uno de los cuerpos. En la ecuación, los parámetros y se utilizan para determinar la trayectoria de la órbita. Hemos medido los siguientes datos. ${\displaystyle r(\theta )={\frac {p}{1-e\cos(\theta )}}}$${\displaystyle r(\theta )}$${\displaystyle p}$${\displaystyle e}$

${\displaystyle \theta }$(en grados)	43	45	52	93	108	116
${\displaystyle r(\theta )}$	4.7126	4.5542	4.0419	2.2187	1.8910	1.7599

Necesitamos encontrar la aproximación de mínimos cuadrados de y para los datos dados.${\displaystyle e}$${\displaystyle p}$

Primero, necesitamos representar e y p en forma lineal. Por lo tanto, vamos a reescribir la ecuación como . Además, se podría ajustar para ápsides expandiendo con un parámetro adicional como , que es lineal tanto en como en la función de base adicional , utilizada para . Usamos la forma original de dos parámetros para representar nuestros datos de observación como:${\displaystyle r(\theta )}$${\displaystyle {\frac {1}{r(\theta )}}={\frac {1}{p}}-{\frac {e}{p}}\cos(\theta )}$${\displaystyle \cos(\theta )}$${\displaystyle \cos(\theta -\theta _{0})=\cos(\theta )\cos(\theta _{0})+\sin(\theta )\sin(\theta _{0})}$${\displaystyle \cos(\theta )}$${\displaystyle \sin(\theta )}$${\displaystyle \tan \theta _{0}=\sin(\theta _{0})/\cos(\theta _{0})}$

${\displaystyle A^{T}A{\binom {x}{y}}=A^{T}b}$donde es y es y se construye con la primera columna siendo el coeficiente de y la segunda columna siendo el coeficiente de y son los valores para los respectivos so y${\displaystyle x}$${\displaystyle {\frac {1}{p}}}$${\displaystyle y}$${\displaystyle {\frac {e}{p}}}$${\displaystyle A}$${\displaystyle {\frac {1}{p}}}$${\displaystyle {\frac {e}{p}}}$${\displaystyle b}$${\displaystyle {\frac {1}{r(\theta )}}}$${\displaystyle A={\begin{bmatrix}1&-0.731354\\1&-0.707107\\1&-0.615661\\1&\ 0.052336\\1&0.309017\\1&0.438371\end{bmatrix}}}$${\displaystyle b={\begin{bmatrix}0.21220\\0.21958\\0.24741\\0.45071\\0.52883\\0.56820\end{bmatrix}}.}$

Al resolverlo obtenemos${\displaystyle {\binom {x}{y}}={\binom {0.43478}{0.30435}}}$

así y${\displaystyle p={\frac {1}{x}}=2.3000}$${\displaystyle e=p\cdot y=0.70001}$

• Mínimos cuadrados bayesianos
• Regresión de Fama-MacBeth
• Mínimos cuadrados no lineales
• Métodos numéricos para mínimos cuadrados lineales
• Identificación de sistemas no lineales

• Dougherty, Christopher (2002). Introducción a la econometría (2.ª ed.). Nueva York: Oxford University Press. pp. 48–113. ISBN 0-19-877643-8.
• Gujarati, Damodar N. ; Porter, Dawn C. (2009). Economía básica (quinta edición). Boston: McGraw-Hill Irwin. págs. 55–96. ISBN 978-0-07-337577-9.
• Heij, Christian; Bóer, Paul; Fransés, Philip H.; Kloek, Teun; van Dijk, Herman K. (2004). Métodos econométricos con aplicaciones en economía y negocios (1ª ed.). Oxford: prensa de la Universidad de Oxford. págs. 76-115. ISBN 978-0-19-926801-6.
• Hill, R. Carter; Griffiths, William E.; Lim, Guay C. (2008). Principios de econometría (3.ª ed.). Hoboken, Nueva Jersey: John Wiley & Sons. pp. 8–47. ISBN 978-0-471-72360-8.
• Wooldridge, Jeffrey (2008). "El modelo de regresión simple". Introducción a la econometría: un enfoque moderno (4.ª ed.). Mason, Ohio: Cengage Learning. pp. 22–67. ISBN 978-0-324-58162-1.