Coordenadas de nacimiento

En física relativista , el diagrama de coordenadas de Born es un diagrama de coordenadas para (parte de) el espacio-tiempo de Minkowski , el espacio-tiempo plano de la relatividad especial . A menudo se utiliza para analizar la experiencia física de los observadores que viajan en un anillo o disco que gira rígidamente a velocidades relativistas , los llamados observadores de Langevin . Este diagrama se atribuye a menudo a Max Born , debido a su trabajo de 1909 sobre la física relativista de un cuerpo en rotación. Para obtener una descripción general de la aplicación de las aceleraciones en el espacio-tiempo plano, consulte Aceleración (relatividad especial) y marco de referencia adecuado (espacio-tiempo plano) .

A partir de la experiencia adquirida en escenarios inerciales (es decir, mediciones en sistemas inerciales), los observadores de Langevin sincronizan sus relojes según la convención estándar de Einstein o mediante una sincronización lenta de relojes , respectivamente (ambas sincronizaciones internas). Para un determinado observador de Langevin, este método funciona perfectamente. En su proximidad inmediata, los relojes están sincronizados y la luz se propaga de forma isótropa en el espacio. Pero la experiencia que surge cuando los observadores intentan sincronizar sus relojes a lo largo de un camino cerrado en el espacio es desconcertante: siempre hay al menos dos relojes vecinos que tienen tiempos diferentes. Para remediar la situación, los observadores acuerdan un procedimiento de sincronización externo (tiempo de coordenadas t —o, para los observadores que viajan en un anillo, un tiempo de coordenadas adecuado para un radio fijo r— ). Mediante este acuerdo, los observadores de Langevin que viajan en un disco que gira rígidamente concluirán, a partir de mediciones de pequeñas distancias entre ellos, que la geometría del disco no es euclidiana. Independientemente del método que utilicen, concluirán que la geometría se aproxima bien a una determinada métrica de Riemann , a saber, la métrica de Langevin–Landau–Lifschitz. Esta, a su vez, se aproxima muy bien a la geometría del plano hiperbólico (con las curvaturas negativas −3 ω ² y −3 ω ²  r ² respectivamente). Pero si estos observadores miden distancias mayores, obtendrán resultados diferentes , ¡dependiendo del método de medición que utilicen! Sin embargo, en todos esos casos, lo más probable es que obtengan resultados que son incompatibles con cualquier métrica de Riemann . En particular, si utilizan la noción más simple de distancia, la distancia de radar, debido a varios efectos como la asimetría ya mencionada, concluirán que la "geometría" del disco no solo no es euclidiana, sino que no es riemanniana.

El disco giratorio no es una paradoja . Cualquiera que sea el método que utilicen los observadores para analizar la situación, al final se encuentran analizando un disco giratorio y no un sistema inercial.

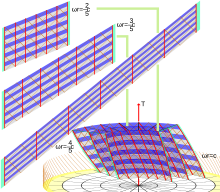
Para fundamentar el diagrama de Born, primero consideramos la familia de observadores de Langevin representados en un diagrama de coordenadas cilíndricas ordinarias para el espacio-tiempo de Minkowski. Las líneas de universo de estos observadores forman una congruencia temporal que es rígida en el sentido de tener un tensor de expansión que se desvanece. Representan observadores que rotan rígidamente alrededor de un eje de simetría cilíndrica.

Desde el elemento de línea

${\displaystyle {\begin{aligned}&\mathrm {d} s^{2}=-\mathrm {d} T^{2}+\mathrm {d} Z^{2}+\mathrm {d} R ^{2}+R^{2}\,\mathrm {d} \Phi ^{2},\;\;\\&-\infty <T,\,Z<\infty ,\;0<R< \infty ,\;-\pi <\Phi <\pi \end{alineado}}}$

Podemos leer inmediatamente un campo de marco que representa los marcos de Lorentz locales de observadores estacionarios (inerciales).

${\displaystyle {\vec {e}}_{0}=\partial _{T},\;\;{\vec {e}}_{1}=\partial _{Z},\;\;{ \vec {e}}_{2}=\partial _{R},\;\;{\vec {e}}_{3}={\frac {1}{R}}\,\partial _{ \Phi }}$

Aquí, hay un campo vectorial unitario temporal , mientras que los otros son campos vectoriales unitarios espaciales ; en cada evento, los cuatro son mutuamente ortogonales y determinan el marco de Lorentz infinitesimal del observador estático cuya línea del mundo pasa por ese evento.${\displaystyle {\vec {e}}_{0}}$

Al impulsar simultáneamente estos campos de marco en la dirección, obtenemos el campo de marco deseado que describe la experiencia física de los observadores de Langevin, es decir${\displaystyle {\vec {e}}_{3}}$

${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,R^{2}}}}\,\partial _{T}+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}}}\;{\frac {1}{R}}\partial _{\Phi }}$

${\displaystyle {\vec {p}}_{1}=\partial _{Z},\;\;{\vec {p}}_{2}=\partial _{R}}$

${\displaystyle {\vec {p}}_{3}={\frac {1}{\sqrt {1-\omega ^{2}\,R^{2}}}}\;{\frac {1}{R}}\,\partial _{\Phi }+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}}}\,\partial _{T}}$

Este marco fue aparentemente introducido por primera vez (implícitamente) por Paul Langevin en 1935; su primer uso explícito parece haber sido por TA Weber, ¡tan recientemente como en 1997! Está definido en la región 0 < R < 1/ω; esta limitación es fundamental, ya que cerca del límite exterior, la velocidad de los observadores de Langevin se acerca a la velocidad de la luz.

Cada curva integral del campo vectorial unitario temporal aparece en el diagrama cilíndrico como una hélice con radio constante (como la curva roja en la Fig. 1). Supongamos que elegimos un observador de Langevin y consideramos a los otros observadores que viajan sobre un anillo de radio R que rota rígidamente con velocidad angular ω. Entonces, si tomamos una curva integral (curva helicoidal azul en la Fig. 1) del vector base espacial , obtenemos una curva que podríamos esperar que pueda interpretarse como una "línea de simultaneidad" para los observadores que viajan sobre el anillo. Pero, como vemos en la Fig. 1, los relojes ideales que llevan estos observadores que viajan sobre el anillo no pueden sincronizarse . Este es nuestro primer indicio de que no es tan fácil como uno podría esperar definir una noción satisfactoria de geometría espacial incluso para un anillo giratorio , ¡mucho menos para un disco giratorio!${\displaystyle {\vec {p}}_{0}}$${\displaystyle {\vec {p}}_{3}}$

Calculando la descomposición cinemática de la congruencia de Langevin, encontramos que el vector de aceleración es

${\displaystyle \nabla _{{\vec {p}}_{0}}{\vec {p}}_{0}={\frac {-\omega ^{2}\,R}{1-\ omega ^{2}\,R^{2}}}\;{\vec {p}}_{2}}$

Esto apunta radialmente hacia adentro y depende únicamente del radio (constante) de cada línea de universo helicoidal. El tensor de expansión se desvanece de manera idéntica, lo que significa que los observadores de Langevin cercanos mantienen una distancia constante entre sí. El vector de vorticidad es

${\displaystyle {\vec {\Omega }}={\frac {\omega }{1-\omega ^{2}\,R^{2}}}\;{\vec {p}}_{1} }$

que es paralela al eje de simetría. Esto significa que las líneas del universo de los vecinos más cercanos de cada observador de Langevin giran alrededor de su propia línea del universo , como lo sugiere la figura 2. Esta es una especie de noción local de "remolino" o vorticidad.

En cambio, nótese que al proyectar las hélices sobre cualquiera de las hipersecciones espaciales ortogonales a las líneas del universo de los observadores estáticos se obtiene un círculo, que es, por supuesto, una curva cerrada. Mejor aún, el vector de base de coordenadas es un campo vectorial de Killing similar al espacio cuyas curvas integrales son curvas cerradas similares al espacio (de hecho, círculos), que además degeneran en curvas cerradas de longitud cero en el eje R = 0. Esto expresa el hecho de que nuestro espacio-tiempo exhibe simetría cilíndrica y también exhibe una especie de noción global de la rotación de nuestros observadores de Langevin.$Estilo de visualización T=T_{0}$${\displaystyle \partial _ {\Phi}}$

En la Fig. 2, la curva magenta muestra cómo giran los vectores espaciales (lo cual se suprime en la figura ya que la coordenada Z no es esencial). Es decir, los vectores no son transportados por Fermi-Walker a lo largo de la línea del mundo, por lo que el marco de Langevin está girando y no es inercial . En otras palabras, en nuestra derivación directa del marco de Langevin, mantuvimos el marco alineado con el vector base de coordenadas radiales . Al introducir una rotación de velocidad constante del marco transportado por cada observador de Langevin alrededor de , podríamos, si quisiéramos, "desgirar" nuestro marco para obtener una versión giroestabilizada.${\displaystyle {\vec {p}}_{2},\;{\vec {p}}_{3}}$${\displaystyle {\vec {p}}_{1}}$${\displaystyle {\vec {p}}_{2},\;{\vec {p}}_{3}}$${\displaystyle \parcial _{R}}$${\displaystyle {\vec {p}}_{1}}$

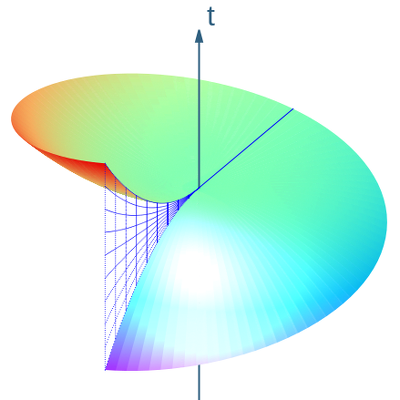
Para obtener el diagrama de Born , enderezamos las líneas helicoidales del mundo de los observadores de Langevin utilizando la simple transformación de coordenadas

${\displaystyle t=T,\;\;z=Z,\;\;r=R,\;\;\phi =\Phi -\omega \,T}$

El nuevo elemento de línea es

${\displaystyle \mathrm {d} s^{2}=-\left(1-\omega ^{2}r^{2}\right)\mathrm {d} t^{2}+2\omega r^ {2}\mathrm {d} t\,\mathrm {d} \phi +\mathrm {d} z^{2}+\mathrm {d} r^{2}+r^{2}\mathrm {d } \phi^{2},}$

${\displaystyle -\infty <t,\,z<\infty ,0<r<{\frac {1}{\omega }},\;-\pi <\phi <\pi }$

Observe los "términos cruzados" que incluyen , que muestran que el diagrama de Born no es un diagrama de coordenadas ortogonales . Las coordenadas de Born también se conocen a veces como coordenadas cilíndricas rotatorias .${\displaystyle \mathrm {d} t\,\mathrm {d} \phi }$

En el nuevo gráfico, las líneas de universo de los observadores de Langevin aparecen como líneas rectas verticales. De hecho, podemos transformar fácilmente los cuatro campos vectoriales que forman el marco de Langevin en el nuevo gráfico. Obtenemos

${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}}$

${\displaystyle {\vec {p}}_{1}=\partial _{z},\;\;{\vec {p}}_{2}=\partial _{r}}$

${\displaystyle {\vec {p}}_{3}={\frac {\sqrt {1-\omega ^{2}\,r^{2}}}{r}}\,\partial _{\phi }+{\frac {\omega \,r}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}}$

Estos son exactamente los mismos campos vectoriales que antes; ¡ahora simplemente están representados en un gráfico de coordenadas diferente!

No hace falta decir que, en el proceso de "desenrollar" las líneas del universo de los observadores de Langevin, que aparecen como hélices en el diagrama cilíndrico, "enrollamos" las líneas del universo de los observadores estáticos, que ahora aparecen como hélices en el diagrama de Born. Nótese también que, al igual que el marco de Langevin, el diagrama de Born solo está definido en la región 0 < r < 1/ω.

Si recalculamos la descomposición cinemática de los observadores de Langevin, es decir, la congruencia temporal , obtendremos, por supuesto, la misma respuesta que obtuvimos antes, sólo que expresada en términos del nuevo gráfico. En concreto, el vector de aceleración es${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}}$

${\displaystyle \nabla _{{\vec {p}}_{0}}\,{\vec {p}}_{0}={\frac {-\omega ^{2}\,r}{1 -\omega ^{2}\,r^{2}}}\,{\vec {p}}_{2}}$

El tensor de expansión se desvanece y el vector de vorticidad es

${\displaystyle {\vec {\Omega }}={\frac {\omega }{1-\omega ^{2}\,r^{2}}}\;{\vec {p}}_{1} }$

El campo covector dual del campo vectorial unitario temporal en cualquier campo de marco representa hipercortes espaciales infinitesimales. Sin embargo, el teorema de integrabilidad de Frobenius establece una fuerte restricción sobre si estos elementos de hiperplano espacial pueden o no "unirse" para formar una familia de hipersuperficies espaciales que sean ortogonales en todas partes a las líneas del mundo de la congruencia. De hecho, resulta que esto es posible, en cuyo caso decimos que la congruencia es ortogonal a la hipersuperficie , si y solo si el vector de vorticidad se desvanece de manera idéntica . Por lo tanto, mientras que los observadores estáticos en el diagrama cilíndrico admiten una familia única de hipercortes ortogonales , los observadores de Langevin no admiten tales hipercortes . En particular, las superficies espaciales en el diagrama de Born son ortogonales a los observadores estáticos, no a los observadores de Langevin . Esta es nuestra segunda indicación (y mucho más directa) de que definir "la geometría espacial de un disco giratorio" no es tan simple como uno podría esperar.$Estilo de visualización T=T_{0}$${\displaystyle t=t_{0}}$

Para comprender mejor este punto crucial, considere las curvas integrales del tercer vector del marco de Langevin.

${\displaystyle {\vec {p}}_{3}={\sqrt {1-\omega ^{2}\,r^{2}}}\,{\frac {1}{r}}\,\partial _{\phi }+{\frac {\omega \,r}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}}$

que pasan por el radio . (Por conveniencia, suprimiremos la coordenada no esencial z de nuestra discusión). Estas curvas se encuentran en la superficie ${\displaystyle \phi =0,\,t=0}$

${\displaystyle \phi +\omega \,t-{\frac {t}{\omega \,r^{2}}}=0,\;\;-\pi <\phi <\pi }$

Se muestra en la figura 3. Nos gustaría considerar esto como un "espacio a la vez" para nuestros observadores de Langevin, pero dos cosas salen mal.

En primer lugar, el teorema de Frobenius nos dice que no son tangentes a ninguna hipersegmentación espacial. De hecho, excepto en el radio inicial, los vectores no se encuentran en nuestra porción . Por lo tanto, si bien encontramos una hipersuperficie espacial, es ortogonal a las líneas del universo de solo algunos de nuestros observadores de Langevin. Debido a que la obstrucción del teorema de Frobenius se puede entender en términos de la incapacidad de los campos vectoriales para formar un álgebra de Lie , esta obstrucción es diferencial, de hecho, teórica de Lie. Es decir, es una especie de obstrucción infinitesimal a la existencia de una noción satisfactoria de hipersegmentaciones espaciales para nuestros observadores rotatorios.${\displaystyle {\vec {p}}_{2},\,{\vec {p}}_{3}}$${\displaystyle {\vec {p}}_{2}}$ ${\displaystyle {\vec {p}}_{2},\,{\vec {p}}_{3}}$

En segundo lugar, como muestra la figura 3, nuestro intento de hipercorte llevaría a una noción discontinua de "tiempo" debido a los "saltos" en las curvas integrales (mostradas como una discontinuidad de cuadrícula de color azul). Alternativamente, podríamos intentar usar un tiempo multivaluado. ¡Ninguna de estas alternativas parece muy atractiva! Esto es evidentemente una obstrucción global . Por supuesto, es una consecuencia de nuestra incapacidad para sincronizar los relojes de los observadores de Langevin que viajan incluso en un solo anillo -digamos el borde de un disco-, mucho menos en un disco entero .

Imaginemos que hemos fijado un cable de fibra óptica alrededor de la circunferencia de un anillo de radio que gira con una velocidad angular constante ω. Queremos calcular el tiempo de viaje de ida y vuelta, medido por un observador montado en el anillo, para un pulso láser enviado en sentido horario y antihorario alrededor del cable. Para simplificar, ignoraremos el hecho de que la luz viaja a través de un cable de fibra óptica a una velocidad algo menor que la de la luz en el vacío, y supondremos que la línea del universo de nuestro pulso láser es una curva nula (¡pero ciertamente no una geodésica nula !).${\displaystyle r_{0}}$

En el elemento de línea Born, pongamos . Esto da${\displaystyle \mathrm {d} s=\mathrm {d} z=\mathrm {d} r=0}$

${\displaystyle (1-\omega ^{2}\,r_{0}^{2})\,\mathrm {d} t^{2}=2\omega \,r_{0}^{2}\,\mathrm {d} t\,\mathrm {d} \phi +r_{0}^{2}\,\mathrm {d} \phi ^{2}}$

o

${\displaystyle \mathrm {d} t_{+}={\frac {r_{0}\,\mathrm {d} \phi }{1-\omega \,r_{0}}},\quad \mathrm {d} t_{-}=-{\frac {r_{0}\,\mathrm {d} \phi }{1+\omega \,r_{0}}}}$

Obtenemos para el tiempo de viaje de ida y vuelta

${\displaystyle \Delta t_{+}=\int _{0}^{2\pi }{\frac {r_{0}\,\mathrm {d} \phi }{1-\omega \,r_{0}}}={\frac {2\pi r_{0}}{1-\omega \,r_{0}}},\quad \Delta t_{-}=\int _{0}^{-2\pi }-{\frac {r_{0}\,\mathrm {d} \phi }{1+\omega \,r_{0}}}={\frac {2\pi r_{0}}{1+\omega \,r_{0}}}}$

Poniendo , encontramos (ω positivo significa rotación en sentido antihorario, ω negativo significa rotación en sentido horario) de modo que los observadores que viajan sobre el anillo pueden determinar la velocidad angular del anillo (medida por un observador estático) a partir de la diferencia entre los tiempos de viaje en sentido horario y antihorario. Esto se conoce como el efecto Sagnac . Es evidentemente un efecto global .${\displaystyle \delta ={\frac {\Delta t_{+}-\Delta t_{-}}{2\,\pi \,r_{0}}}}$${\displaystyle \omega _{+,-}={\frac {-1\pm {\sqrt {1+\delta ^{2}}}}{r_{0}\,\delta }}}$

Deseamos comparar la apariencia de las geodésicas nulas en la carta cilíndrica y la carta de Born.

En el diagrama cilíndrico, las ecuaciones geodésicas se leen

${\displaystyle {\ddot {T}}=0,\;\;{\ddot {Z}}=0,\;\;{\ddot {R}}-R\,{\dot {\Phi }}^{2}=0,\;\;{\ddot {\Phi }}+{\frac {2}{R}}\,{\dot {\Phi }}\,{\dot {R}}=0.}$

Obtenemos inmediatamente las primeras integrales

${\displaystyle {\dot {T}}=E,\;\;{\dot {Z}}=P,\;\;{\dot {\Phi }}={\frac {L}{R^{2}}}.}$

Conectando estos a la expresión obtenida del elemento de línea estableciendo , obtenemos${\displaystyle \mathrm {d} s^{2}=0}$

${\displaystyle {\dot {R}}^{2}=E^{2}-P^{2}-{\frac {L^{2}}{R^{2}}}\geq 0}$

de donde vemos que el radio mínimo de una geodésica nula está dado por

${\displaystyle E^{2}-P^{2}-{\frac {L^{2}}{R_{\mathrm {min} }^{2}}}=0\quad }$es decir,${\displaystyle \quad R_{\mathrm {min} }={\frac {|L|}{\sqrt {E^{2}-P^{2}}}}}$

por eso

${\displaystyle {\dot {R}}^{2}=L^{2}\left({\frac {1}{R_{\mathrm {min} }^{2}}}-{\frac {1}{R^{2}}}\right).}$

Ahora podemos resolver para obtener las geodésicas nulas como curvas parametrizadas por un parámetro afín, de la siguiente manera:

${\displaystyle {\begin{aligned}R&={\sqrt {(E^{2}-P^{2})\,s^{2}+L^{2}/(E^{2}-P^{2})}}=\\&={\sqrt {(E^{2}-P^{2})\,s^{2}+R_{\mathrm {min} }^{2}}},\\T&=T_{0}+E\,s,\\[1em]Z&=Z_{0}+P\,s,\\\Phi &=\Phi _{0}+\operatorname {arctan} \left({\frac {E^{2}-P^{2}}{L}}\,s\right)=\\&=\Phi _{0}+\operatorname {arctan} \left({\frac {\sqrt {E^{2}-P^{2}}}{R_{\mathrm {min} }\,\operatorname {sgn} {(L)}}}\,s\right).\end{aligned}}}$

Más útil para nuestros propósitos es la observación de que la trayectoria de una geodésica nula (su proyección en cualquier hipersegmento espacial ) es, por supuesto, una línea recta, dada por${\displaystyle T=T_{0}}$

${\displaystyle R=R_{\mathrm {min} }\,\sec(\Phi -\Phi _{0}).}$

Para obtener el radio mínimo de la línea que pasa por dos puntos (del mismo lado del punto de aproximación más cercano al origen), resolvemos

${\displaystyle R_{1}=R_{\mathrm {min} }\,\sec(\Phi _{1}-\Phi _{0}),\;\;R_{2}=R_{\mathrm {min} }\,\sec(\Phi _{2}-\Phi _{0})}$

Lo cual da

${\displaystyle R_{\mathrm {min} }={\frac {R_{1}\,R_{2}\,|\sin(\Phi _{2}-\Phi _{1})|}{\sqrt {R_{1}^{2}-2\,R_{1}\,R_{2}\,\cos(\Phi _{2}-\Phi _{1})+R_{2}^{2}}}}.}$

Consideremos ahora el caso más simple, las geodésicas nulas radiales (R _min = L = 0, E = 1, P = 0). Una geodésica nula radial con límite externo puede escribirse en la forma

${\displaystyle T=s,\;Z=Z_{0},\;R=s,}$

${\displaystyle \Phi =\mathrm {const.} =\omega \,R_{0}}$

con el radio R ₀ del anillo montado sobre el observador de Langevin (véase la figura 4). Transformando al diagrama de Born, encontramos que la trayectoria se puede escribir como

${\displaystyle r=r_{0}-{\frac {\phi }{\omega }}.}$

Las pistas aparecen ligeramente dobladas en el diagrama de Born (ver la curva verde en la Fig. 4). En la sección Transformación al diagrama de Born vemos que en el diagrama de Born no podemos referirnos correctamente a estas "pistas" como "proyecciones", ya que para el observador de Langevin no existe una hipersegmentación ortogonal para t = t _{0 (ver Fig. 3).}

De manera similar, para geodésicas nulas radiales con límite interno, obtenemos

${\displaystyle r={\frac {\phi }{\omega }}}$

representado como una curva roja en la figura 4.

Obsérvese que para enviar un pulso láser hacia el observador estacionario S en R = 0, el observador de Langevin L tiene que apuntar ligeramente hacia atrás para corregir su propio movimiento. Dando la vuelta a las cosas, tal como esperaría un cazador de patos, para enviar un pulso láser hacia el observador de Langevin que viaja en un anillo que gira en sentido antihorario, el observador central tiene que apuntar, no a la posición actual de este observador, sino a la posición a la que llegará justo a tiempo para interceptar la señal. Estas familias de geodésicas nulas radiales de límite interno y externo representan curvas muy diferentes en el espacio-tiempo y sus proyecciones no concuerdan para ω > 0.

De manera similar, las geodésicas nulas entre observadores de Langevin que se desplazan sobre anillos aparecen ligeramente dobladas hacia adentro en el gráfico de Born, si las geodésicas se propagan con la dirección de la rotación (ver la curva verde en la figura 5). Para ver esto, escriba la ecuación de una geodésica nula en el gráfico cilíndrico en la forma

${\displaystyle T=R_{\mathrm {min} }\,\tan(\Phi ),}$

${\displaystyle R=R_{\mathrm {min} }\,\sec(\Phi ).}$

Transformando a coordenadas de Born, obtenemos las ecuaciones

${\displaystyle t=r_{\mathrm {min} }\,\tan(\phi +\omega \,t),}$

${\displaystyle r=r_{\mathrm {min} }\,\sec(\phi +\omega \,t).}$

Eliminando ϕ se obtiene

${\displaystyle r={\sqrt {r_{\mathrm {min} }^{2}+t^{2}}}}$

lo que demuestra que la geodésica parece efectivamente doblarse hacia adentro (ver Figura 6). También encontramos que

${\displaystyle \phi =-\omega \,t+\operatorname {arctan} (t/r_{\mathrm {min} }).}$

Para geodésicas nulas que se propagan contra la rotación (curva roja en la figura 5) obtenemos

${\displaystyle r={\sqrt {r_{\mathrm {min} }^{2}+t^{2}}},}$

${\displaystyle \phi =-\omega \,t-\operatorname {arctan} (t/r_{\mathrm {min} })}$

y la geodésica se curva ligeramente hacia afuera. Esto completa la descripción de la apariencia de las geodésicas nulas en la carta de Born, ya que cada geodésica nula es radial o tiene algún punto de aproximación más cercano al eje de simetría cilíndrica.

Nótese (ver Figura 5) que un observador que se desplaza sobre un anillo y que intenta enviar un pulso láser a otro observador que se desplaza sobre un anillo debe apuntar ligeramente hacia delante o hacia atrás respecto de su coordenada angular, como se indica en la tabla de Born, para compensar el movimiento de rotación del objetivo. Nótese también que la imagen presentada aquí es totalmente compatible con nuestra expectativa (ver Aspecto del cielo nocturno ) de que un observador en movimiento verá que la posición aparente de otros objetos en su esfera celeste se desplaza hacia la dirección de su movimiento.

Incluso en el espacio-tiempo plano, resulta que los observadores que aceleran (incluso los que aceleran linealmente; véase las coordenadas de Rindler ) pueden emplear varias nociones de distancia distintas pero operativamente significativas. Tal vez la más simple de ellas sea la distancia de radar .

Consideremos cómo un observador estático en R=0 podría determinar su distancia a un observador que se desplaza sobre el anillo en R = R ₀ . En el evento C envía un pulso de radar hacia el anillo, que golpea la línea del universo de un observador que se desplaza sobre el anillo en A ′ y luego regresa al observador central en el evento C ″. (Véase el diagrama de la derecha en la figura 7.) A continuación, divide el tiempo transcurrido (medido por un reloj ideal que lleva consigo) por dos. No es difícil ver que obtiene para esta distancia simplemente R ₀ (en el diagrama cilíndrico), o r ₀ (en el diagrama de Born).

De manera similar, un observador que cabalga sobre el anillo puede determinar su distancia al observador central enviando un pulso de radar, en el evento A hacia el observador central, que golpea su línea de universo en el evento C ′ y regresa al observador que cabalga sobre el anillo en el evento A ″. (Véase el diagrama de la izquierda en la Fig. 7.) No es difícil ver que obtiene para esta distancia (en el gráfico cilíndrico) o (en el gráfico de Born), un resultado que es algo menor que el obtenido por el observador central. Esto es una consecuencia de la dilatación del tiempo: el tiempo transcurrido para un observador que cabalga sobre el anillo es menor por el factor que el tiempo para el observador central. Así, mientras que la distancia de radar tiene un significado operativo simple, ni siquiera es simétrica .${\displaystyle R_{0}{\sqrt {1-\omega ^{2}\,R_{0}^{2}}}}$${\displaystyle r_{0}{\sqrt {1-\omega ^{2}\,r_{0}^{2}}}}$${\displaystyle {\sqrt {1-\omega ^{2}\,r_{0}^{2}}}}$

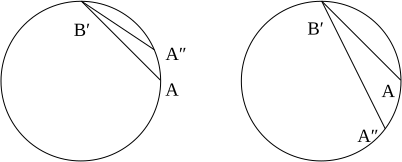
Para enfatizar este punto crucial, compare las distancias de radar obtenidas por dos observadores que viajan en anillo con coordenadas radiales R = R ₀ . En el diagrama de la izquierda de la Fig. 8, podemos escribir las coordenadas del evento A como

${\displaystyle T=0,\;Z=0,\;X=R_{0},Y=0}$

y podemos escribir las coordenadas del evento B ′ como

${\displaystyle T=2\,R_{0}\,\sin \left({\frac {\Phi }{2}}\right),\;Z=0,}$

${\displaystyle X=R_{0}\cos(\Phi ),\;Y=R_{0}\sin(\Phi )}$

Escribiendo el tiempo propio transcurrido desconocido como , ahora escribimos las coordenadas del evento A ″ como${\displaystyle \Delta s}$

${\displaystyle T={\frac {\Delta s}{\sqrt {1-\omega ^{2}\,R_{0}^{2}}}},\;Z=0}$

${\displaystyle X=R_{0}\cos \left({\frac {\omega \,\Delta s}{\sqrt {1-\omega ^{2}\,R_{0}^{2}}}}\right),\;Y=R_{0}\sin \left({\frac {\omega \,\Delta s}{\sqrt {1-\omega ^{2}\,R_{0}^{2}}}}\right)}$

Al exigir que los segmentos de línea que conectan estos eventos sean nulos, obtenemos una ecuación que, en principio, podemos resolver para Δ s . Resulta que este procedimiento da una ecuación no lineal bastante complicada, por lo que simplemente presentamos algunos resultados numéricos representativos. Con R ₀ = 1, Φ = π/2 y ω = 1/10, encontramos que la distancia de radar de A a B es de aproximadamente 1,311, mientras que la distancia de B a A es de aproximadamente 1,510. Como ω tiende a cero, ambos resultados tienden hacia √ 2 = 1,414 (ver también la Figura 5).

A pesar de estas discrepancias, que pueden resultar desalentadoras, no es imposible diseñar un diagrama de coordenadas que se adapte a la descripción de la experiencia física de un solo observador de Langevin, o incluso de un solo observador que acelera arbitrariamente en el espacio-tiempo de Minkowski. Pauri y Vallisneri han adaptado el procedimiento de sincronización del reloj de Märzke-Wheeler para diseñar coordenadas adaptadas que denominan coordenadas de Märzke-Wheeler (véase el artículo citado más abajo). En el caso del movimiento circular constante, este diagrama está, de hecho, muy relacionado con la noción de distancia de radar "en general" desde un observador de Langevin determinado.

Como se mencionó anteriormente, por diversas razones, la familia de observadores de Langevin no admite ninguna familia de hipersegmentos ortogonales. Por lo tanto, estos observadores simplemente no pueden asociarse con ninguna división del espacio-tiempo en una familia de sucesivas "segmentos de tiempo constante".

Sin embargo, debido a que la congruencia de Langevin es estacionaria , podemos imaginar reemplazar cada línea del universo en esta congruencia por un punto . Es decir, podemos considerar el espacio cociente del espacio-tiempo de Minkowski (o más bien, la región 0 < R < 1/ ω ) por la congruencia de Langevin, que es una variedad topológica tridimensional . Mejor aún, podemos colocar una métrica de Riemann en esta variedad cociente, convirtiéndola en una variedad de Riemann tridimensional , de tal manera que la métrica tenga un significado operacional simple.

Para ver esto, considere el elemento de línea Born

${\displaystyle \mathrm {d} s^{2}=-(1-\omega ^{2}\,r^{2})\,\mathrm {d} t^{2}+2\,\omega \,r^{2}\,\mathrm {d} t\,\mathrm {d} \phi +\mathrm {d} z^{2}+\mathrm {d} r^{2}+r^{2}\,\mathrm {d} \phi ^{2},}$

${\displaystyle -\infty <t,z<\infty ,\;\;0<r<{\frac {1}{\omega }},\;\;-\pi <\phi <\pi .}$

Fijando d s ² = 0 y resolviendo d t obtenemos

${\displaystyle \mathrm {d} t_{+}={\frac {\omega \,r^{2}\,\mathrm {d} \phi +{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}},}$

${\displaystyle \mathrm {d} t_{-}={\frac {\omega \,r^{2}\,\mathrm {d} \phi -{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}}.}$

El tiempo propio transcurrido para un destello de radar de ida y vuelta emitido por un observador de Langevin es entonces

${\displaystyle {\sqrt {1-\omega ^{2}\,r^{2}}}\;{\frac {\mathrm {d} t_{+}-\mathrm {d} t_{-}}{2}}={\sqrt {\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {r^{2}\,\mathrm {d} \phi ^{2}}{1-\omega ^{2}\,r^{2}}}}}.}$

Por lo tanto, en nuestra variedad cociente, el elemento de línea de Riemann

${\displaystyle \mathrm {d} \sigma ^{2}=\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {r^{2}\,\mathrm {d} \phi ^{2}}{1-\omega ^{2}\,r^{2}}},}$

${\displaystyle -\infty <t<\infty ,\;\;0<r<{\frac {1}{\omega }},\;\;-\pi <\phi <\pi }$

corresponde a la distancia entre observadores de Langevin infinitesimalmente cercanos . La llamaremos métrica de Langevin-Landau-Lifschitz y podemos llamar a esta noción de distancia distancia de radar "en lo pequeño" .

Esta métrica fue dada por primera vez por Langevin , pero la interpretación en términos de distancia de radar "en lo pequeño" se debe a Lev Landau y Evgeny Lifshitz , quienes generalizaron la construcción para trabajar para el cociente de cualquier variedad lorentziana por una congruencia temporal estacionaria .

Si adoptamos el marco común

${\displaystyle \theta ^{\hat {1}}=\mathrm {d} z,\;\;\theta ^{\hat {2}}=\mathrm {d} r,\;\;\theta ^{\hat {3}}={\frac {r\,\mathrm {d} \phi }{\sqrt {1-\omega ^{2}\,r^{2}}}}}$

Podemos calcular fácilmente el tensor de curvatura de Riemann de nuestra variedad cociente tridimensional. Tiene sólo dos componentes independientes no triviales,

${\displaystyle {R^{\hat {2}}}_{{\hat {3}}{\hat {2}}{\hat {3}}}={\frac {-3\,\omega ^{2}}{(1-\omega ^{2}r^{2})^{2}}}=-3\,\omega ^{2}+O(\omega ^{4}\,r^{2}),}$

${\displaystyle {R^{\hat {3}}}_{{\hat {2}}{\hat {3}}{\hat {2}}}={\frac {-3\,\omega ^{2}\,r^{2}}{(1-\omega ^{2}r^{2})^{3}}}=-3\,\omega ^{2}\,r^{2}+O(\omega ^{4}\,r^{4}).}$

Así pues, en cierto sentido, la geometría de un disco giratorio es curva , como afirmó Theodor Kaluza (sin pruebas) ya en 1910. De hecho, hasta el segundo orden en ω tiene la geometría del plano hiperbólico, tal como afirmó Kaluza.

Advertencia: como hemos visto, hay muchas nociones posibles de distancia que pueden emplear los observadores de Langevin montados en un disco que gira rígidamente, por lo que las afirmaciones que hacen referencia a "la geometría de un disco giratorio" siempre requieren una calificación cuidadosa.

Para enfatizar este punto importante, usemos la métrica de Landau-Lifschitz para calcular la distancia entre un observador de Langevin que viaja sobre un anillo con radio R ₀ y un observador estático central. Para hacer esto, solo necesitamos integrar nuestro elemento de línea sobre la pista geodésica nula apropiada. De nuestro trabajo anterior, vemos que debemos reemplazar

${\displaystyle \mathrm {d} r={\frac {\mathrm {d} \phi }{\omega }},\,\mathrm {d} z=0}$

en nuestro elemento de línea e integrarlo

${\displaystyle \int _{0}^{\Delta }\mathrm {d} \sigma =\int \limits _{0}^{r_{0}}{\left(1+{\frac {\omega ^{2}r^{2}}{1-\omega ^{2}r^{2}}}\right)^{\frac {1}{2}}}\,\mathrm {d} r.}$

Esto da

${\displaystyle \Delta =\int _{0}^{r_{0}}{\frac {\mathrm {d} r}{\sqrt {1-\omega ^{2}\,r^{2}}}}={\frac {\arcsin(\omega r_{0})}{\omega }}=r_{0}+{\frac {\omega ^{2}\,r_{0}^{3}}{6}}+O(r_{0}^{5}).}$

Como ahora estamos tratando con una métrica de Riemann, esta noción de distancia es, por supuesto, simétrica al intercambiar los dos observadores, a diferencia de la distancia de radar "en general". Los valores dados por esta noción están en contradicción con las distancias de radar "en general" calculadas en la sección anterior. Además, como hasta el segundo orden la métrica de Landau-Lifschitz concuerda con la convención de sincronización de Einstein, vemos que el tensor de curvatura que acabamos de calcular tiene importancia operativa: mientras que la distancia de radar "en general" entre pares de observadores de Langevin ciertamente no es una noción de distancia de Riemann , la distancia entre pares de observadores de Langevin cercanos corresponde a una distancia de Riemann, dada por la métrica de Langevin-Landau-Lifschitz. (En la feliz frase de Howard Percy Robertson , esto es kinematics im Kleinen .)

Una forma de ver que todas las nociones razonables de distancia espacial para nuestros observadores de Langevin coinciden para los observadores cercanos es demostrar, siguiendo a Nathan Rosen , que para cualquier observador de Langevin, un observador inercial que se mueve instantáneamente también obtendrá las distancias dadas por la métrica de Langevin-Landau-Lifschitz, para distancias muy pequeñas.

• Paradoja de Ehrenfest , para un tema a veces controvertido y que a menudo se estudia utilizando el diagrama de Born.
• Giroscopio de fibra óptica
• Coordenadas de Rindler , para otro gráfico de coordenadas útil adaptado a otra familia importante de observadores acelerados en el espacio-tiempo de Minkowski ; este artículo también enfatiza la existencia de nociones distintas de distancia que pueden ser empleadas por dichos observadores.
• Efecto Sagnac

Algunos artículos de interés histórico:

• Nacido, M. (1909). "Die Theorie des starren Elektrons in der Kinematik des Relativitäts-Prinzipes". Ana. Física . 30 (11): 1–56. Código bibliográfico : 1909AnP...335....1B. doi : 10.1002/andp.19093351102.
  • Traducción de Wikisource: La teoría del electrón rígido en la cinemática del principio de relatividad
• Ehrenfest, P. (1909). "Gleichförmige Rotation protagonizada por Körper und Relativitätstheorie". Física. Z.​ 10 : 918. Código bibliográfico : 1909PhyZ...10..918E.
  • Traducción de Wikisource: Rotación uniforme de cuerpos rígidos y teoría de la relatividad
• Langevin, P. (1935). "Remarques au sujet de la Note de Prunier". CR Acad. Ciencia. París . 200 : 48.

Algunas referencias clásicas:

• Grøn, Ø. (1975). "Descripción relativista de un disco giratorio". Am. J. Phys . 43 (10): 869–876. Código Bibliográfico :1975AmJPh..43..869G. doi :10.1119/1.9969.
• Landau, LD y Lifschitz, EM (1980). La teoría clásica de campos (4.ª ed.) . Londres: Butterworth-Heinemann. ISBN 0-7506-2768-9. Véase la Sección 84 para la métrica de Landau-Lifschitz en el cociente de una variedad lorentziana por una congruencia estacionaria ; consulte el problema al final de la Sección 89 para la aplicación a los observadores de Langevin.

Fuentes recientes seleccionadas:

• Rizzi, G. y Ruggiero, ML (2004). Relatividad en sistemas rotatorios . Dordrecht: Kluwer. ISBN 1-4020-1805-3. Este libro contiene un valioso estudio histórico de Øyvind Grøn y otros artículos sobre la paradoja de Ehrenfest y controversias relacionadas, así como un artículo de Lluis Bel que analiza la congruencia de Langevin. En este libro se pueden encontrar cientos de referencias adicionales.
• Pauri, Massimo y Vallisneri, Michele (2000). "Coordenadas de Märzke-Wheeler para observadores acelerados en relatividad especial". Encontrado. Phys. Lett . 13 (5): 401–425. arXiv : gr-qc/0006095 . Código Bibliográfico :2000gr.qc.....6095P. doi :10.1023/A:1007861914639. S2CID  15097773.Estudia un gráfico de coordenadas construido utilizando la distancia de radar "en general" de un solo observador de Langevin. Véase también la versión impresa.

• El disco giratorio rígido en la relatividad, por Michael Weiss (1995), de las preguntas frecuentes de sci.physics .