Bisección
En geometría , la bisección es la división de algo en dos partes iguales o congruentes (que tienen la misma forma y tamaño). Por lo general, implica una línea bisectriz , también llamada bisectriz . Los tipos de bisectrices considerados con más frecuencia son la bisectriz de segmento , una línea que pasa por el punto medio de un segmento dado , y la bisectriz de ángulo , una línea que pasa por el vértice de un ángulo (que lo divide en dos ángulos iguales). En el espacio tridimensional , la bisección generalmente se realiza mediante un plano bisectriz , también llamado bisectriz .
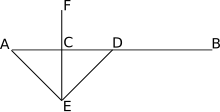
Bisectriz de un segmento de línea perpendicular
Definición

- La bisectriz perpendicular de un segmento de línea es una línea que se encuentra con el segmento en su punto medio de manera perpendicular.
- La bisectriz perpendicular de un segmento de línea también tiene la propiedad de que cada uno de sus puntos es equidistante de los extremos del segmento AB:
(D) .
La prueba se desprende del teorema de Pitágoras :
La propiedad (D) se utiliza generalmente para la construcción de una bisectriz perpendicular:
Construcción con regla y compás

En geometría clásica, la bisección es una sencilla construcción con compás y regla , cuya posibilidad depende de la capacidad de trazar arcos de radios iguales y centros diferentes:
El segmento se divide en dos al dibujar círculos que se intersecan con el mismo radio , cuyos centros son los puntos finales del segmento. La línea determinada por los puntos de intersección de los dos círculos es la mediatriz del segmento.
Debido a que la construcción de la mediatriz se realiza sin conocer el punto medio del segmento , la construcción se utiliza para determinar la intersección de la mediatriz y el segmento de línea.
Esta construcción se utiliza de hecho cuando se construye una línea perpendicular a una línea dada en un punto dado : se dibuja un círculo cuyo centro es tal que interseca la línea en dos puntos , y la perpendicular a construir es el segmento que la biseca .
Ecuaciones
Si son los vectores de posición de dos puntos , entonces su punto medio es y el vector es un vector normal de la bisectriz del segmento de línea perpendicular. Por lo tanto, su ecuación vectorial es . Insertando y expandiendo la ecuación se obtiene la ecuación vectorial
(V)
Con uno se obtiene la ecuación en forma de coordenadas:
(DO)
O explícitamente:
(E) ,
donde , , y .
Aplicaciones
Las bisectrices de segmentos de líneas perpendiculares se utilizaron para resolver varios problemas geométricos:
- Construcción del centro de un círculo de Tales ,
- Construcción del centro del círculo excéntrico de un triángulo,
- Los límites del diagrama de Voronoi consisten en segmentos de dichas líneas o planos.

Bisectrices de segmentos de rectas perpendiculares en el espacio
- La bisectriz perpendicular de un segmento de línea es un plano que corta al segmento en su punto medio perpendicularmente.
Su ecuación vectorial es literalmente la misma que en el caso del plano:
(V)
Con uno se obtiene la ecuación en forma de coordenadas:
(C3)
La propiedad (D) (ver arriba) también es literalmente verdadera en el espacio:
(D) El plano bisectriz perpendicular de un segmento tiene para cualquier punto la propiedad: .
Bisectriz de un ángulo

La bisectriz de un ángulo divide el ángulo en dos ángulos de igual medida. Un ángulo solo tiene una bisectriz. Cada punto de la bisectriz de un ángulo es equidistante de los lados del ángulo.
La bisectriz interior o interna de un ángulo es la línea, semirrecta o segmento de línea que divide un ángulo de menos de 180° en dos ángulos iguales. La bisectriz exterior o externa es la línea que divide el ángulo suplementario (de 180° menos el ángulo original), formado por un lado que forma el ángulo original y la prolongación del otro lado, en dos ángulos iguales. [1]
Para bisecar un ángulo con regla y compás , se dibuja un círculo cuyo centro es el vértice. El círculo corta al ángulo en dos puntos: uno en cada cateto. Usando cada uno de estos puntos como centro, se dibujan dos círculos del mismo tamaño. La intersección de los círculos (dos puntos) determina una línea que es la bisectriz del ángulo.
La demostración de la exactitud de esta construcción es bastante intuitiva y se basa en la simetría del problema. La trisección de un ángulo (dividirlo en tres partes iguales) no se puede lograr solo con compás y regla (esto fue demostrado por primera vez por Pierre Wantzel ).
Las bisectrices interna y externa de un ángulo son perpendiculares . Si el ángulo está formado por las dos líneas dadas algebraicamente como y entonces las bisectrices interna y externa están dadas por las dos ecuaciones [2] : p.15
Triángulo
Concurrencias y colineales

Las bisectrices de dos ángulos exteriores y la bisectriz del otro ángulo interior son concurrentes. [3] : p.149
Tres puntos de intersección, cada uno de una bisectriz de un ángulo externo con el lado extendido opuesto , son colineales (caen en la misma línea uno que el otro). [3] : p. 149
Tres puntos de intersección, dos de ellos entre una bisectriz de un ángulo interior y el lado opuesto, y el tercero entre la otra bisectriz de un ángulo exterior y la prolongación del lado opuesto, son colineales. [3] : p. 149
Teorema de la bisectriz del ángulo

El teorema de la bisectriz de un ángulo se ocupa de las longitudes relativas de los dos segmentos en los que se divide el lado de un triángulo mediante una línea que biseca el ángulo opuesto. Iguala sus longitudes relativas a las longitudes relativas de los otros dos lados del triángulo.
Longitudes
Si las longitudes de los lados de un triángulo son , el semiperímetro y A es el ángulo opuesto al lado , entonces la longitud de la bisectriz interna del ángulo A es [3] : p. 70
o en términos trigonométricos, [4]
Si la bisectriz interna del ángulo A en el triángulo ABC tiene longitud y si esta bisectriz divide al lado opuesto a A en segmentos de longitudes m y n , entonces [3] : p.70
donde b y c son las longitudes de los lados opuestos a los vértices B y C; y el lado opuesto a A está dividido en la proporción b : c .
Si las bisectrices internas de los ángulos A, B y C tienen longitudes y , entonces [5]
No existen dos triángulos no congruentes que compartan el mismo conjunto de longitudes de bisectrices de tres ángulos internos. [6] [7]
Triángulos enteros
Existen triángulos enteros con bisectriz de ángulo racional .
Cuadrilátero
Las bisectrices de los ángulos internos de un cuadrilátero convexo forman un cuadrilátero cíclico (es decir, los cuatro puntos de intersección de las bisectrices de los ángulos adyacentes son concíclicos ), [8] o son concurrentes . En el último caso, el cuadrilátero es un cuadrilátero tangencial .
Rombo
Cada diagonal de un rombo biseca ángulos opuestos.
Cuadrilátero ex-tangencial
El excentro de un cuadrilátero extangencial se encuentra en la intersección de seis bisectrices de ángulos. Estas son las bisectrices de ángulos internos en dos ángulos de vértice opuestos, las bisectrices de ángulos externos (bisectriz de ángulos suplementarios) en los otros dos ángulos de vértice y las bisectrices de ángulos externos en los ángulos formados donde se intersecan las extensiones de lados opuestos .
Parábola
La tangente a una parábola en cualquier punto biseca el ángulo entre la línea que une el punto al foco y la línea que parte del punto y es perpendicular a la directriz.
Bisectrices de los lados de un polígono
Triángulo
Medianas
Cada una de las tres medianas de un triángulo es un segmento de línea que pasa por un vértice y el punto medio del lado opuesto, por lo que divide en dos ese lado (aunque en general no de manera perpendicular). Las tres medianas se cortan entre sí en un punto que se llama baricentro del triángulo, que es su centro de masa si tiene densidad uniforme; por lo tanto, cualquier línea que pase por el baricentro de un triángulo y uno de sus vértices divide en dos el lado opuesto. El baricentro está dos veces más cerca del punto medio de cualquiera de los lados que del vértice opuesto.
Mediatrices perpendiculares
La mediatriz perpendicular interior de un lado de un triángulo es el segmento, que cae completamente sobre el triángulo y dentro de él, de la línea que divide perpendicularmente ese lado. Las tres mediatrices de los tres lados de un triángulo se cortan en el circuncentro (el centro del círculo que pasa por los tres vértices). Por lo tanto, cualquier línea que pase por el circuncentro de un triángulo y sea perpendicular a un lado divide ese lado en dos.
En un triángulo acutángulo, el circuncentro divide las mediatrices interiores de los dos lados más cortos en proporciones iguales. En un triángulo obtusángulo, las mediatrices interiores de los dos lados más cortos (que se extienden más allá de sus lados opuestos hasta el circuncentro) están divididas por sus respectivos lados triangulares que se cortan en proporciones iguales. [9] : Corolarios 5 y 6
Para cualquier triángulo las bisectrices perpendiculares interiores están dadas por y donde los lados son y el área es [9] : Teoría 2
Cuadrilátero
Las dos bimedianas de un cuadrilátero convexo son los segmentos de línea que unen los puntos medios de los lados opuestos, por lo que cada uno de ellos biseca dos lados. Las dos bimedianas y el segmento de línea que une los puntos medios de las diagonales son concurrentes en un punto llamado "centroide del vértice" y todos están bisecados por este punto. [10] : p.125
Las cuatro "alturas" de un cuadrilátero convexo son las perpendiculares a un lado que pasan por el punto medio del lado opuesto, y que, por lo tanto, dividen en dos el último lado. Si el cuadrilátero es cíclico (está inscrito en un círculo), estas alturas son concurrentes en (todas se encuentran en) un punto común llamado "anticentro".
El teorema de Brahmagupta establece que si un cuadrilátero cíclico es ortodiagonal (es decir, tiene diagonales perpendiculares ), entonces la perpendicular a un lado desde el punto de intersección de las diagonales siempre biseca al lado opuesto.
La construcción de la bisectriz perpendicular forma un cuadrilátero a partir de las bisectrices perpendiculares de los lados de otro cuadrilátero.
Bisectrices de área y bisectrices de perímetro
Triángulo
Hay una infinidad de líneas que bisecan el área de un triángulo . Tres de ellas son las medianas del triángulo (que conectan los puntos medios de los lados con los vértices opuestos), y son concurrentes en el baricentro del triángulo ; de hecho, son las únicas bisectrices de área que pasan por el baricentro. Otras tres bisectrices de área son paralelas a los lados del triángulo; cada una de ellas interseca a los otros dos lados de modo de dividirlos en segmentos con las proporciones . [11] Estas seis líneas son concurrentes de tres en tres: además de que las tres medianas son concurrentes, cualquier mediana es concurrente con dos de las bisectrices de área paralelas a los lados.
La envolvente de la infinitud de las bisectrices del área es un deltoides (definido ampliamente como una figura con tres vértices conectados por curvas que son cóncavas al exterior del deltoides, haciendo que los puntos interiores sean un conjunto no convexo). [11] Los vértices del deltoides están en los puntos medios de las medianas; todos los puntos dentro del deltoides están en tres bisectrices del área diferentes, mientras que todos los puntos fuera de él están en solo una. [1] Los lados del deltoides son arcos de hipérbolas que son asintóticos a los lados extendidos del triángulo. [11] La relación entre el área de la envolvente de las bisectrices del área y el área del triángulo es invariante para todos los triángulos, y es igual a 0,019860... o menos del 2%.
Una hendidura de un triángulo es un segmento de línea que divide en dos el perímetro del triángulo y tiene un extremo en el punto medio de uno de los tres lados. Las tres hendiduras coinciden en (todas pasan por) el centro del círculo de Spieker , que es el círculo inscrito del triángulo medial . Las hendiduras son paralelas a las bisectrices de los ángulos.
Un divisor de un triángulo es un segmento de línea que tiene un punto final en uno de los tres vértices del triángulo y divide en dos el perímetro. Los tres divisores coinciden en el punto de Nagel del triángulo.
Cualquier línea que pase por un triángulo y divida tanto el área como el perímetro del triángulo por la mitad pasa por el incentro del triángulo (el centro de su circunferencia inscrita). Hay uno, dos o tres de estos para cualquier triángulo dado. Una línea que pase por el incentro biseca una parte del área o del perímetro si y solo si también biseca la otra. [12]
Paralelogramo
Cualquier línea que pase por el punto medio de un paralelogramo biseca el área [11] y el perímetro.
Círculo y elipse
Todas las bisectrices del área y del perímetro de un círculo u otra elipse pasan por el centro , y cualquier cuerda que pase por el centro biseca el área y el perímetro. En el caso de un círculo, son los diámetros del círculo.
Bisectrices de diagonales
Paralelogramo
Las diagonales de un paralelogramo se bisecan entre sí.
Cuadrilátero
Si un segmento de línea que conecta las diagonales de un cuadrilátero biseca ambas diagonales, entonces este segmento de línea (la línea de Newton ) es a su vez bisecado por el centroide del vértice.
Bisectrices de volumen
Un plano que divide dos aristas opuestas de un tetraedro en una proporción dada también divide el volumen del tetraedro en la misma proporción. Por lo tanto, cualquier plano que contenga un bimediano (conector de los puntos medios de las aristas opuestas) de un tetraedro biseca el volumen del tetraedro [13] [14] : págs. 89-90
Referencias
- ^ Weisstein, Eric W. "Bisectriz del ángulo exterior". De MathWorld, un recurso web de Wolfram.
- ^ España, Barry. Cónicas analíticas , Dover Publications, 2007 (orig. 1957).
- ^ abcde Johnson, Roger A., Geometría euclidiana avanzada , Dover Publ., 2007 (orig. 1929).
- ^ Oxman, Victor. "Sobre la existencia de triángulos con longitudes dadas de un lado y dos bisectrices de ángulos adyacentes", Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf
- ^ Simons, Stuart. Mathematical Gazette 93, marzo de 2009, 115-116.
- ^ Mironescu, P., y Panaitopol, L., "La existencia de un triángulo con longitudes de bisectrices de ángulos prescritas", American Mathematical Monthly 101 (1994): 58–60.
- ^ Oxman, Victor, "Una prueba puramente geométrica de la unicidad de un triángulo con bisectrices de ángulos prescritas", Forum Geometricorum 8 (2008): 197–200.
- ^ Weisstein, Eric W. "Cuadrilátero". De MathWorld, un recurso web de Wolfram. http://mathworld.wolfram.com/Quadrilateral.html
- ^ ab Mitchell, Douglas W. (2013), "Bisectrices perpendiculares de los lados de un triángulo", Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
- ^ Altshiller-Court, Nathan, Geometría universitaria , Dover Publ., 2007.
- ^ abcd Dunn, Jas. A.; Pretty, Jas. E. (mayo de 1972). "Dividir un triángulo en dos". The Mathematical Gazette . 56 (396): 105–108. doi :10.2307/3615256. JSTOR 3615256.
- ^ Kodokostas, Dimitrios, "Ecualizadores de triángulos", Mathematics Magazine 83, abril de 2010, págs. 141-146.
- ^ Weisstein, Eric W. "Tetrahedron". De MathWorld, un recurso web de Wolfram. http://mathworld.wolfram.com/Tetrahedron.html
- ^ Altshiller-Court, N. "El tetraedro". Cap. 4 en Modern Pure Solid Geometry : Chelsea, 1979.
Enlaces externos
- La bisectriz del ángulo en el punto de corte del nudo
- Definición de bisectriz de un ángulo. Referencia abierta de matemáticas con aplicación interactiva
- Definición de bisectriz de línea. Referencia abierta de matemáticas con aplicación interactiva
- Bisectriz de línea perpendicular. Con aplicación interactiva
- Instrucciones animadas para dividir un ángulo en dos y dividir una línea en dos usando un compás y una regla
- Weisstein, Eric W. "Bisectriz de línea". MathWorld .
Este artículo incorpora material de Bisectriz de un ángulo en PlanetMath , que se encuentra bajo la licencia Creative Commons Attribution/Share-Alike License .












































