Filtro de Chebyshev
Filtros electrónicos analógicos lineales |
|---|
Los filtros Chebyshev son filtros analógicos o digitales que tienen una caída más pronunciada que los filtros Butterworth y tienen ondulación de banda de paso (tipo I) o ondulación de banda de rechazo (tipo II). Los filtros Chebyshev tienen la propiedad de minimizar el error entre la característica idealizada y la real del filtro en el rango de frecuencia de funcionamiento del filtro, [1] [2] pero lo logran con ondulaciones en la banda de paso. Este tipo de filtro recibe su nombre de Pafnuty Chebyshev porque sus características matemáticas se derivan de los polinomios de Chebyshev . Los filtros Chebyshev de tipo I suelen denominarse "filtros Chebyshev", mientras que los filtros de tipo II suelen denominarse "filtros Chebyshev inversos". [3] Debido a la ondulación de banda de paso inherente a los filtros Chebyshev, se prefieren los filtros con una respuesta más suave en la banda de paso pero una respuesta más irregular en la banda de rechazo para ciertas aplicaciones. [4]
Filtros Chebyshev tipo I (filtros Chebyshev)

Los filtros Chebyshev de tipo I son los tipos más comunes de filtros Chebyshev. La respuesta de ganancia (o amplitud ), , en función de la frecuencia angular del filtro de paso bajo de orden th es igual al valor absoluto de la función de transferencia evaluada en :
donde es el factor de ondulación, es la frecuencia de corte y es un polinomio de Chebyshev de orden ésimo.
La banda de paso exhibe un comportamiento de ondulación equitativa, con la ondulación determinada por el factor de ondulación . En la banda de paso, el polinomio de Chebyshev alterna entre -1 y 1, por lo que la ganancia del filtro alterna entre máximos en y mínimos en .
El factor de ondulación ε está relacionado con la ondulación de la banda de paso δ en decibeles mediante:
En la frecuencia de corte, la ganancia vuelve a tener el valor , pero continúa cayendo hacia la banda de rechazo a medida que aumenta la frecuencia. Este comportamiento se muestra en el diagrama de la derecha. La práctica común de definir la frecuencia de corte en −3 dB no suele aplicarse a los filtros Chebyshev; en cambio, el corte se toma como el punto en el que la ganancia cae hasta el valor de la ondulación por última vez.
La frecuencia de 3 dB está relacionada con:
El orden de un filtro Chebyshev es igual al número de componentes reactivos (por ejemplo, inductores ) necesarios para realizar el filtro utilizando electrónica analógica .
Se puede obtener una reducción aún más pronunciada si se permite la ondulación en la banda de rechazo, permitiendo ceros en el eje en el plano complejo. Si bien esto produce una supresión casi infinita en y cerca de estos ceros (limitada por el factor de calidad de los componentes, los parásitos y los factores relacionados), la supresión general en la banda de rechazo se reduce. El resultado se denomina filtro elíptico , también conocido como filtro de Cauer.
Polos y ceros
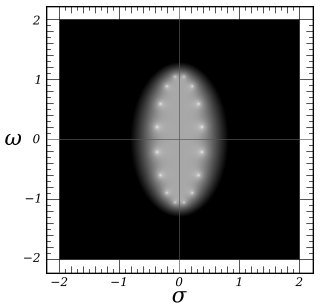
Para simplificar, se supone que la frecuencia de corte es igual a la unidad. Los polos de la función de ganancia del filtro de Chebyshev son los ceros del denominador de la función de ganancia. Si se utiliza la frecuencia compleja , esto ocurre cuando:
Definiendo y utilizando la definición trigonométrica de los polinomios de Chebyshev obtenemos:
Resolviendo para
donde los valores múltiples de la función arcocoseno se hacen explícitos utilizando el índice entero . Los polos de la función de ganancia de Chebyshev son entonces:
Usando las propiedades de las funciones trigonométricas e hiperbólicas, esto puede escribirse en forma explícitamente compleja:
donde y
Esto puede verse como una ecuación paramétrica y demuestra que los polos se encuentran en una elipse en el espacio centrada en con un semieje real de longitud y un semieje imaginario de longitud de
La función de transferencia
La expresión anterior da los polos de la ganancia . Para cada polo complejo, hay otro que es el conjugado complejo, y para cada par conjugado hay dos más que son los negativos del par. La función de transferencia debe ser estable, de modo que sus polos sean aquellos de la ganancia que tienen partes reales negativas y, por lo tanto, se encuentran en el semiplano izquierdo del espacio de frecuencias complejo. La función de transferencia está dada entonces por
donde están solo aquellos polos de la ganancia con signo negativo delante del término real, obtenido de la ecuación anterior.
El retraso del grupo

El retardo de grupo se define como la derivada de la fase con respecto a la frecuencia angular:
La ganancia y el retardo de grupo para un filtro Chebyshev tipo I de quinto orden con ε=0,5 se representan en el gráfico de la izquierda. Su banda de rechazo no tiene ondulaciones, pero las ondulaciones del retardo de grupo en su banda de paso indican que los diferentes componentes de frecuencia tienen un retardo diferente, lo que junto con las ondulaciones de ganancia en su banda de paso da como resultado una distorsión de la forma de onda.
Incluso modificaciones de pedidos
Los filtros Chebyshev de orden par implementados con elementos pasivos, típicamente inductores, capacitores y líneas de transmisión, con terminaciones de igual valor en cada lado no pueden implementarse con la función de transferencia Chebyshev tradicional sin el uso de bobinas acopladas, lo que puede no ser deseable o factible, particularmente en las frecuencias más altas. Esto se debe a la incapacidad física para acomodar los ceros de reflexión de Chebyshev de orden par que resultan en valores de matriz de dispersión S12 que exceden el valor S12 en . Si no es factible diseñar el filtro con una de las terminaciones aumentada o disminuida para acomodar la banda de paso S12, entonces la función de transferencia Chebyshev debe modificarse para mover el cero de reflexión de orden par más bajo a mientras se mantiene la respuesta de rizado equitativo de la banda de paso. [5]
La modificación necesaria implica mapear cada polo de la función de transferencia de Chebyshev de manera que mapee el cero de reflexión de frecuencia más baja a cero y los polos restantes según sea necesario para mantener la banda de paso de ondulación uniforme. El cero de reflexión de frecuencia más baja se puede encontrar a partir de los nodos de Chebyshev , . La función de mapeo de polos de Chebyshev completa se muestra a continuación. [5]
Dónde:
n es el orden del filtro (debe ser par)
P es un polo de función de transferencia de Chebyshev tradicional
P' es el polo mapeado para la función de transferencia de orden par modificada.
"Semiplano izquierdo" indica utilizar la raíz cuadrada que contiene un valor real negativo.
Una vez completada, se crea una función de transferencia de rizado equitativo de reemplazo con valores de matriz de dispersión de reflexión cero para S12 de uno y S11 de cero cuando se implementa con redes pasivas con terminación igual. La siguiente ilustración muestra un filtro Chebyshev de octavo orden modificado para admitir redes pasivas con terminación igual de orden par al reubicar el cero de reflexión de frecuencia más baja de una frecuencia finita a 0 mientras se mantiene una respuesta de frecuencia de banda de paso de rizado equitativo.
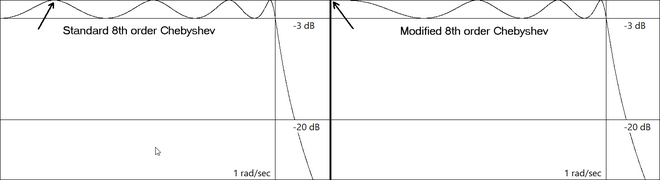
Las fórmulas de valores de elementos LC en la topología de Cauer no son aplicables a la función de transferencia de Chebyshev modificada de orden par y no se pueden utilizar. Por lo tanto, es necesario calcular los valores LC a partir de fracciones continuas tradicionales de la función de impedancia, que pueden derivarse del coeficiente de reflexión , que a su vez puede derivarse de la función de transferencia.
Pedido mínimo
Para diseñar un filtro Chebyshev utilizando el número mínimo requerido de elementos, el orden mínimo del filtro Chebyshev se puede calcular de la siguiente manera. [6] Las ecuaciones solo tienen en cuenta los filtros Chebyshev de paso bajo estándar. Incluso las modificaciones de orden y los ceros de transmisión de banda de detención finitos introducirán un error que las ecuaciones no tienen en cuenta.
dónde:
y son la frecuencia de ondulación de la banda de paso y la atenuación máxima de ondulación en dB
y son la frecuencia de la banda de parada y la atenuación en esa frecuencia en dB
es el número mínimo de polos, el orden del filtro.
ceil [] es una función de redondeo al siguiente número entero.
Configuración de la atenuación de corte
La atenuación de corte de la banda de paso para los filtros Chebyshev suele ser la misma que la atenuación de rizado de la banda de paso, establecida mediante el cálculo anterior. Sin embargo, muchas aplicaciones, como los diplexores y los triplexores [5] , requieren una atenuación de corte de -3,0103 dB para obtener las reflexiones necesarias. Otras aplicaciones especializadas pueden requerir otros valores específicos para la atenuación de corte por diversas razones. Por lo tanto, es útil tener un medio disponible para establecer la atenuación de corte de la banda de paso de Chebyshev independientemente de la atenuación de rizado de la banda de paso, como -1 dB, -10 dB, etc. La atenuación de corte se puede establecer mediante la escala de frecuencia de los polos de la función de transferencia.
El factor de escala puede determinarse mediante manipulación algebraica directa de la función de filtro de Chebyshev definitoria, , que incluye y . Se requiere la definición general de la función de Chebyshev, que puede derivarse de las ecuaciones de los polinomios de Chebyshev y la función de Chebyshev inversa, . Para mantener los números reales para los valores de , se pueden usar identidades hiperbólicas complejas para reescribir las ecuaciones como, y .
Usando álgebra simple sobre las ecuaciones y referencias anteriores, la expresión para escalar cada polo de Chebyshev es:
Dónde:
es el polo reubicado posicionado para establecer la atenuación de corte deseada.
es un poste de corte ondulado que se encuentra sobre el óvalo.
es la ondulación de atenuación de la banda de paso en dB (0,05 dB, 1 dB, etc.)).
es la atenuación de banda de paso deseada en la frecuencia de corte en dB (1 dB, 3 dB, 10 dB, etc.)
es el número de polos (el orden del filtro).
Una rápida comprobación de la ecuación anterior utilizando la atenuación de ondulación de banda de paso para la atenuación de corte de banda de paso revela que el ajuste del polo será 1,0 para este caso, que es lo que se espera.
Ajuste de atenuación de corte modificado de orden par
En el caso de los filtros Chebyshev diseñados con una ondulación de banda de paso modificada para filtros pasivos con terminación uniforme, el cálculo de la frecuencia de atenuación debe incluir el ajuste de orden par, realizando la operación de ajuste de orden par en la frecuencia de atenuación calculada. Esto hace que la aritmética del ajuste de orden par sea un poco más sencilla, ya que la frecuencia se puede tratar como una variable real, en este caso .
Dónde:
es el polo reubicado posicionado para establecer la atenuación de corte deseada.
es un polo de corte de ondulación que ha sido modificado para bandas de paso de orden uniforme.
es la ondulación de atenuación de la banda de paso en dB (0,05 dB, 1 dB, etc.)).
es la atenuación de banda de paso deseada en la frecuencia de corte en dB (1 dB, 3 dB, 10 dB, etc.)
es el número de polos (el orden del filtro).
es el nodo de Chebyshev de orden par más pequeño
Filtros Chebyshev tipo II (filtros Chebyshev inversos)

También conocido como filtro Chebyshev inverso, el filtro Chebyshev Tipo II es menos común porque no se desvía tan rápido como el Tipo I y requiere más componentes. No tiene ondulación en la banda de paso, pero sí tiene ondulación equi en la banda de rechazo. La ganancia es:
En la banda de supresión, el polinomio de Chebyshev oscila entre -1 y 1, de modo que la ganancia oscilará entre cero y
y la frecuencia más pequeña en la que se alcanza este máximo es la frecuencia de corte . El parámetro ε está relacionado con la atenuación de la banda de rechazo γ en decibeles mediante:
Para una atenuación de banda de rechazo de 5 dB, ε = 0,6801; para una atenuación de 10 dB, ε = 0,3333. La frecuencia f 0 = ω 0 /2 π es la frecuencia de corte. La frecuencia f H de 3 dB está relacionada con f 0 mediante:
Polos y ceros

Suponiendo que la frecuencia de corte es igual a la unidad, los polos de la ganancia del filtro Chebyshev son los ceros del denominador de la ganancia:
Los polos de ganancia del filtro Chebyshev tipo II son los inversos de los polos del filtro tipo I:
donde . Los ceros del filtro Chebyshev tipo II son los ceros del numerador de la ganancia:
Los ceros del filtro Chebyshev tipo II son por lo tanto los inversos de los ceros del polinomio de Chebyshev.
para .
La función de transferencia
La función de transferencia está dada por los polos en el semiplano izquierdo de la función de ganancia, y tiene los mismos ceros, pero estos ceros son simples en lugar de ceros dobles.
El retraso del grupo

En el gráfico de la izquierda se representan la ganancia y el retardo de grupo de un filtro Chebyshev tipo II de quinto orden con ε=0,1. Se puede observar que hay ondulaciones en la ganancia en la banda de rechazo, pero no en la banda de paso.
Incluso modificaciones de pedidos
Al igual que los filtros de orden par de Chebyshev, el filtro de orden par Chebyshev II estándar no se puede implementar con elementos pasivos igualmente terminados sin el uso de bobinas acopladas, lo que puede no ser deseable o factible. En el caso de Chebyshev Ii, esto se debe a la atenuación finita de S12 en la banda de detención. [5] Sin embargo, los filtros Chebyshev II de orden par se pueden modificar trasladando el cero de transmisión finito de frecuencia más alta a infinito, mientras se mantienen las funciones de ondulación equitativa de la banda de detención de Chebyshev II. Para hacer esta traducción, se utiliza una función de Chebyshev modificada de orden par en lugar de la función de Chebyshev estándar para definir los polos de Chebyshev II necesarios para crear la función de transferencia de Chebyshev II modificada de orden par. Los ceros se crean utilizando las raíces del polinomio de Chebyshev modificado de orden par , que son los nodos de Chebyshev modificados de orden par .
La siguiente ilustración muestra un filtro Chebyshev inverso de octavo orden modificado para soportar redes pasivas igualmente terminadas de orden par, reubicando el cero de transmisión de frecuencia más alta desde una frecuencia finita a mientras se mantiene una respuesta de frecuencia de banda de detención de ondulación equitativa.

Pedido mínimo
Para diseñar un filtro Chebyshev inverso utilizando el número mínimo requerido de elementos, el orden mínimo del filtro Chebyshev inverso se puede calcular de la siguiente manera. [7] Las ecuaciones tienen en cuenta únicamente los filtros Chebyshev inversos de paso bajo estándar. Incluso las modificaciones de orden introducirán errores que las ecuaciones no tienen en cuenta. Las ecuaciones son idénticas a las utilizadas para el orden mínimo del filtro Chebyshev, con definiciones de variables ligeramente diferentes.
dónde:
y son la frecuencia de la banda de paso y la atenuación en esa frecuencia en dB
y son la frecuencia de la banda de parada y la atenuación mínima de la banda de parada en dB
es el número mínimo de polos, el orden del filtro.
ceil [] es una función de redondeo al siguiente número entero.
Configuración de la atenuación de corte
La atenuación de corte estándar descrita es la misma que la atenuación de ondulación de la banda de paso. Sin embargo, al igual que en los filtros Chebyshev, es útil establecer la atenuación de corte en un valor deseado y por las mismas razones. La configuración de la atenuación de corte de Chebyshev II es la misma que para la atenuación de corte de Chebyshev, excepto que las entradas de atenuación aritmética y ondulación se invierten en la ecuación y los polos y ceros se multiplican por el resultado, en lugar de dividirse por en el caso de Chebyshev.
Ajuste de atenuación de corte modificado de orden par
El mismo ajuste de orden par a los polos y ceros que se utilizó para la atenuación de corte modificada de orden par de Chebyshev también se puede utilizar para el caso de Chebyshev II, excepto que los polos se multiplican por el resultado.
Implementación
Topología de Cauer
Se puede realizar un filtro de paso bajo Chebyshev LC pasivo utilizando una topología Cauer . Los valores del inductor o capacitor de un filtro prototipo Chebyshev de orden th se pueden calcular a partir de las siguientes ecuaciones: [8]
G 1 , G k son los valores del elemento capacitor o inductor. f H , la frecuencia de 3 dB se calcula con:
Los coeficientes A , γ , β , A k y B k pueden calcularse a partir de las siguientes ecuaciones:
¿Dónde está la ondulación de la banda de paso en decibeles? El número se redondea a partir del valor exacto .
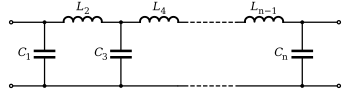
Los valores de G k calculados pueden convertirse en capacitores en derivación e inductores en serie como se muestra a la derecha, o pueden convertirse en capacitores en serie e inductores en derivación. Por ejemplo,
- C 1 derivación = G 1 , L 2 serie = G 2 , ...
o
- Derivación L 1 = G 1 , serie C 1 = G 2 , ...
Tenga en cuenta que cuando G 1 es un condensador en derivación o un inductor en serie, G 0 corresponde a la resistencia de entrada o conductancia, respectivamente. La misma relación se aplica a G n+1 y G n . El circuito resultante es un filtro de paso bajo normalizado. Mediante transformaciones de frecuencia y escala de impedancia , el filtro de paso bajo normalizado se puede transformar en filtros de paso alto , paso de banda y filtro de banda supresora de cualquier frecuencia de corte o ancho de banda deseados .
Digital
Al igual que con la mayoría de los filtros analógicos, el filtro Chebyshev se puede convertir a una forma recursiva digital (de tiempo discreto) mediante la transformada bilineal . Sin embargo, como los filtros digitales tienen un ancho de banda finito, la forma de respuesta del filtro Chebyshev transformado se deforma . Alternativamente, se puede utilizar el método de transformada Z adaptada , que no deforma la respuesta.
Comparación con otros filtros lineales
La siguiente ilustración muestra los filtros Chebyshev junto a otros tipos de filtros comunes obtenidos con el mismo número de coeficientes (quinto orden):

Los filtros Chebyshev son más nítidos que el filtro Butterworth ; no son tan nítidos como el elíptico , pero muestran menos ondulaciones en el ancho de banda.
Temas avanzados sobre filtros de Chebyshev
La flexibilidad de diseño del filtro Chebyshev puede aumentarse mediante métodos de diseño más avanzados documentados en esta sección. Se pueden insertar ceros de transmisión en la banda de detención para neutralizar frecuencias no deseadas específicas o aumentar la atenuación de corte, o se pueden insertar fuera del eje para obtener un retardo de grupo más deseable . Se pueden crear filtros de paso de banda Chebyshev asimétricos que contengan un número diferente de polos en cada lado de la banda de paso para cumplir con los requisitos de diseño asimétrico de frecuencia de manera más eficiente. Las bandas de paso de rizado equitativo por las que se conocen los filtros Chebyshev se pueden restringir a un porcentaje de la banda de paso para cumplir con los requisitos de diseño de manera más eficiente que solo requieren que una parte de la banda de paso sea de rizado equitativo. [9]
Ceros de transmisión de Chebyshev
Los filtros Chebyshev pueden diseñarse con ceros de transmisión finitos colocados arbitrariamente en la banda de rechazo, manteniendo al mismo tiempo una banda de paso de ondulación uniforme. Los ceros de banda de rechazo a lo largo del eje se utilizan generalmente para eliminar frecuencias no deseadas. Los ceros de banda de rechazo a lo largo del eje real o los ceros de banda de rechazo cuádruple en el plano complejo se pueden utilizar para modificar el retardo de grupo a una forma más deseable. El diseño de los ceros de transmisión utiliza polinomios característicos, K(S), para colocar los ceros de transmisión y reflexión, que a su vez se utilizan para crear la función de transferencia, , [10]
El cálculo de K(S) se basa en la siguiente igualdad observada. [10]
para todos , pares conjugados imaginarios , pares conjugados cuaternarios o pares con signos opuestos reales.
Dado que la magnitud es siempre uno en la banda de paso ( ), los términos racionales e irracionales deben variar entre 0 y 1. Por lo tanto, si solo se utiliza el término racional para crear la función característica, se espera una respuesta de equi-rizado en la banda de paso y se esperan polos característicos (ceros de transmisión) en absoluto .
El proceso de diseño para K(S) utilizando la expresión anterior se muestra a continuación.
Utilice la solución positiva para pares reales e imaginarios . Utilice la solución positiva real e imaginaria conjugada para pares complejos de cuatrillizos .
debe normalizarse de tal manera que , si es necesario.
El término racional solo indica que se debe conservar la parte racional del producto y descartar la parte irracional. El término racional se puede obtener realizando manualmente la aritmética polinómica o con el atajo que se muestra a continuación, que es una solución derivada de la aritmética polinómica y utiliza coeficientes binomiales . El algoritmo es extremadamente eficiente si los coeficientes binomiales se implementan a partir de una tabla de búsqueda de valores precalculados.
Cuando todos los valores M se establecen en uno, entonces será la ecuación estándar de Chebyshev, lo cual es esperado ya que todos los ceros de transmisión son it . Los filtros Chebyshev de transmisión finita de orden par tienen la misma limitación que el caso de todos los polos en el sentido de que no se pueden construir utilizando redes pasivas igualmente terminadas. La misma modificación de orden par se puede hacer a los polinomios característicos de orden par, , para hacer posibles las implementaciones de redes pasivas igualmente terminadas. Sin embargo, la modificación de orden par también moverá ligeramente los ceros de transmisión finitos. Este movimiento se puede mitigar significativamente proponiendo los ceros de transmisión con la inversa de la modificación de orden par utilizando el nodo Chebyshev más bajo , .
Ejemplo de transmisión simple de ceros
Diseñe un filtro Chebyshev de 3 polos con una banda de paso de 1 dB, un cero de transmisión a 2 rad/seg y un cero de transmisión a :
Para encontrar la función de transferencia, haga lo siguiente. [10] [11]
Para obtener el valor del semiplano izquierdo, factorice el numerador y el denominador para obtener las raíces. Descarte todas las raíces del semiplano derecho del denominador, la mitad de las raíces repetidas en el numerador y reconstruya con las raíces restantes. En general, normalice a 1 en .
Para confirmar que el ejemplo es correcto, a continuación se muestra el gráfico con una ondulación de banda de paso de 1 dB, una frecuencia de corte de 1 rad/seg y una banda de detención cero en 2 rad/seg.

Filtro de paso de banda asimétrico
Los filtros de paso de banda de Chebyshev pueden diseñarse con una respuesta de frecuencia asimétrica geométricamente colocando el número deseado de ceros de transmisión en cero e infinito con el uso de la forma más generalizada de la ecuación de ceros de transmisión de Chebyshev anterior, [10] y que se muestra a continuación. Las ecuaciones siguientes consideran una banda de paso normalizada en frecuencia de 1 a . Si el número de ceros de transmisión en 0 no es el mismo que el número de ceros de transmisión en , el filtro será geométricamente asimétrico. El filtro también será asimétrico si los ceros de transmisión finitos no se colocan simétricamente con respecto a la frecuencia central geométrica, que en este caso es . Existe una restricción en cuanto a que el filtro debe ser de orden par neto, es decir, la suma de todos los polos debe ser par, para que la ecuación asimétrica produzca resultados utilizables. También se pueden crear ceros de transmisión cuádruples reales y complejos utilizando esta técnica y son útiles para modificar la respuesta de retardo de grupo , al igual que en el caso de paso bajo. La derivación de la ecuación característica, , para crear un filtro de paso de banda de Chebyshev asimétrico se muestra a continuación.
debe normalizarse de tal manera que , si es necesario.
Ejemplo asimétrico simple
Diseñe un filtro Chebyshev asimétrico con una ondulación de banda de paso de 1 dB de 1 a 2 rad/seg, un cero de transmisión en , y tres ceros de transmisión en 0. Aplicando los valores numéricos a las ecuaciones anteriores, los polinomios característicos, , se pueden calcular de la siguiente manera.
Descartando la parte irracional y normalizando a 1 en s=j:
Utilice el mismo proceso que en el caso de paso bajo para encontrar desde , utilizando una constante para escalar la magnitud. [10] [11]
Al reconstruir el denominador a partir de los polos del semiplano izquierdo, será necesario establecer la magnitud de modo que los ceros de reflexión se produzcan a 0 dB. Para ello, se debe escalar de modo que = -1 dB en las frecuencias de esquina de la banda de paso, y . Una vez logrado, la función de transferencia final para el filtro Chebyshev asimétrico diseñado se muestra a continuación.
La evaluación en s=j y en s=2j produce un valor de -1dB en ambos casos, lo que garantiza que el ejemplo se ha sintetizado correctamente. La respuesta de frecuencia se muestra a continuación, mostrando una respuesta de banda de paso de rizado equitativo de 1dB de Chebyshev para , atenuación de corte de -1dB en los bordes de la banda de paso, atenuación de -60dB/década hacia , atenuación de -20dB/década hacia , y pendientes pronunciadas de estilo Chebyshev cerca de los bordes de la banda de paso.

Restringiendo la ondulación de la banda de paso
El diseño estándar de un filtro Chebyshev de paso bajo crea una banda de paso con ondulación equitativa que comienza desde 0 rad/seg hasta un valor normalizado de frecuencia de 1 rad/seg. Sin embargo, algunos requisitos de diseño no necesitan una banda de paso con ondulación equitativa en las frecuencias bajas. Un filtro Chebyshev estándar con ondulación equitativa completa para esta aplicación daría como resultado un filtro sobredimensionado. Restringir la ondulación equitativa a un porcentaje definido de la banda de paso crea un diseño más eficiente, reduciendo el tamaño del filtro y eliminando potencialmente uno o dos componentes, lo que es útil para maximizar la eficiencia del espacio en la placa y minimizar los costos de producción para artículos fabricados en masa. [9]
La ondulación de la banda de paso restringida se puede lograr diseñando un filtro de paso de banda Chebyshev asimétrico utilizando las técnicas descritas anteriormente en este artículo con un lado de paso alto asimétrico de orden 0 (sin ceros de transmisión en 0) y un conjunto a la frecuencia de ondulación restringida. El orden del lado de paso bajo es N-1 para filtros de orden impar, N-2 para filtros modificados de orden par y N para filtros de orden par estándar. Esto da como resultado un S12 menor que la unidad en , que es típico del diseño estándar de Chebyshev de orden par, por lo que para los diseños estándar de Chebyshev de orden par, el proceso está completo en este paso. Será necesario insertar un solo cero de reflexión en para diseños de orden impar y dos ceros de reflexión en para diseños modificados de orden par. Los ceros de reflexión agregados introducen un error notable en la banda de paso que probablemente sea objetable. Este error se puede eliminar de manera rápida y precisa reposicionando los ceros de reflexión finitos con el uso del método de Newton para sistemas de ecuaciones .
Aplicación del método de Newton
Para posicionar los ceros de reflexión con el método de Newton se necesitan tres datos:
- La ubicación de cada mínimo de ondulación de la banda de paso que existe en frecuencias más altas que la frecuencia de ondulación restringida.
- El valor de la magnitud normalizada , es decir , en la frecuencia de constricción y en cada mínimo por encima de la frecuencia de constricción. Las referencias futuras a esta función se indicarán como o
- La matriz jacobiana de derivada parcial de para la frecuencia de constricción y en cada mínimo por encima de la frecuencia de constricción. con respecto a cada cero de reflexión.
Dado que las ecuaciones características de Chebyshev, , tienen todos los ceros de reflexión ubicados en el eje, y todos los ceros de transmisión ya sea en el eje o simétricos con respecto al eje (requerido para la implementación del elemento pasivo), las ubicaciones de los mínimos de ondulación de la banda de paso se pueden obtener factorizando el numerador de la derivada de , , con el uso de un algoritmo de búsqueda de raíces . Las raíces de este polinomio serán las frecuencias mínimas de la banda de paso. se puede obtener a partir de las definiciones estándar de derivadas de polinomios , y es .
Las derivadas parciales se pueden calcular digitalmente con , sin embargo, la derivada parcial continua generalmente proporciona mayor precisión y menor tiempo de convergencia, y se recomienda. Para obtener las derivadas parciales continuas de con respecto a los ceros de las reflexiones, se debe obtener una expresión continua para que fuerce en todo momento. Esto se puede lograr expresando como una función de sus pares de raíces conjugadas, como se muestra a continuación.
Donde incluye solo ceros de reflexión y transmisión finitos, y se refieren al número de pares conjugados de ceros de reflexión y transmisión, y y son los pares conjugados de ceros de reflexión y transmisión. El término impar representa el único cero de reflexión en 0 que ocurre en los filtros de Chebyshev de orden impar. Tenga en cuenta que si se emplean ceros de transmisión de cuatrillizos, la expresión debe modificarse para dar cabida a términos de cuatrillizos. Se ve por inspección que siempre que en la expresión anterior.
Dado que solo se necesita el movimiento de los ceros de reflexión para dar forma a la banda de paso de Chebyshev, la expresión de la derivada parcial solo debe realizarse en los términos, y los términos se tratan como una constante. Para ayudar en la determinación de la expresión de la derivada parcial para cada , la expresión anterior puede reescribirse, como se muestra a continuación.
Donde designa un par conjugado de reflexión cero específico.
La derivada de esta expresión con respecto a se puede calcular fácilmente siguiendo las reglas de derivadas estándar . La constante requiere la división de los términos para mantener la integridad de la función. La forma más fácil de hacerlo es multiplicar por el inverso de los términos que se movieron al frente. La expresión diferenciable se puede reescribir de la siguiente manera.
La derivada parcial se puede determinar aplicando procedimientos de derivada estándar y luego simplificando. El resultado se muestra a continuación.
Dado que las únicas frecuencias relevantes son las frecuencias en el punto de constricción y las raíces de , la matriz jacobiana se puede construir de la siguiente manera.
Donde es la frecuencia límite de constricción, y son la magnitud de las raíces de los mínimos de la banda de paso restante, y son los ceros de reflexión.
Suponiendo que la atenuación de corte del filtro es la misma que la magnitud de la ondulación, el valor de es 1 en todos los casos , por lo que las entradas del vector solución son todas 1, y las ecuaciones iterativas para resolver el método de Newton son
La convergencia se logra cuando la suma de todos los valores es lo suficientemente pequeña para la aplicación, generalmente entre 1.e-05 y 1.e-16. Para filtros más grandes, puede ser necesario restringir el tamaño de cada uno para evitar oscilaciones excesivas al comienzo de la convergencia, y restringir el tamaño de cada uno para mantener sus valores dentro del rango de ondulación restringido durante la convergencia.
Ejemplo de banda de paso restringida
Diseñe un filtro Chebyshev de 7 polos con una banda de paso con rizado equitativo de 1 dB restringida al 55 % de la banda de paso.
Paso 1: Diseñe los polinomios característicos para una respuesta de frecuencia asimétrica de 0,45 a 1 con 6 polos de paso bajo en , y 0 polos de paso alto utilizando el proceso de síntesis asimétrica anterior (use frecuencia de esquina = 0,45).

| Paso 1: |
|---|
| Banda de paso de ondulación restringida del 55 % y 7 polos para |
| Banda de paso de ondulación equitativa de 1 dB |
| Escala de frecuencia lineal |
Paso 2: Inserte un único cero de reflexión en el del paso 1. (se requerirán dos adiciones de cero de reflexión para filtros modificados de orden par)

| Paso 2: |
|---|
| Banda de paso de ondulación restringida del 55 % y 7 polos para |
| Banda de paso de ondulación equitativa de 1 dB |
| Escala de frecuencia lineal |
Paso 3: Determine a partir de la banda de paso las frecuencias derivadas cero calculando los valores reales o imaginarios positivos de las raíces de , y sustituya la raíz más baja con la frecuencia de constricción de 0,45 para .
| 1 | 0,45 | 0,64670785 | 0,89924235 |
| 2 | 0,45 | 0,68010003 | 0,9147864 |
| 3 | 0,45 | 0,6710597 | 0,91089712 |
| 4 | 0,45 | 0,66969972 | 0,91042253 |
| 5 | 0,45 | 0,66967763 | 0,9104163 |
| 6 | 0,45 | 0,66967762 | 0,9104163 |
Paso 4 : Determinar el valor de en cada punto cero restringido y derivado.
| 1 | 0,45 | 0,64035786 | 0,89703503 |
| 2 | 1.3886545 | 1.1638033 | 1.0148793 |
| 3 | 1.045108 | 1.0133721 | 0,99991225 |
| 4 | 1.0007289 | 1.0001094 | 0,99998768 |
| 5 | 1.0000002 | 1 | 1 |
| 6 | 1 | 1 | 1 |
Paso 5 : Cree el vector B para las ecuaciones lineales restando los valores objetivo en cada frecuencia, que en este caso son todos 1 debido a que la atenuación de corte es igual a la atenuación de ondulación de la banda de paso en este ejemplo específico. en la frecuencia de corte de .
| 1 | -0,55 | -0,35964214 | -0,10296497 |
| 2 | 0,38865445 | 0,1638033 | 0,014879269 |
| 3 | 0,045108043 | 0,013372137 | -8.7751135e-05 |
| 4 | 7.2893112e-04 | 1.0943442e-04 | -1.2324941e-05 |
| 5 | 1.7276985e-07 | 5.2176787e-09 | -2.6640391e-09 |
| 6 | 1.8873791e-14 | 1.5765167e-14 | -2.553513e-15 |
Paso 6: Determinar la matriz jacobiana de la derivada parcial de para cada uno con respecto a cada reflexión cero, ,
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
Paso 7 : Obtenga los movimientos de los ceros de reflexión resolviendo el conjunto lineal de ecuaciones utilizando el vector B del paso 5.
| 1 | -0,033937389 | -0,040973291 | -0,0054977233 | .02680 |
| 2 | 0,010159103 | 0,010436353 | 0,001099011 | .00723149 |
| 3 | 0,0018170271 | 0,001314472 | 1.090765e-04 | .00108019 |
| 4 | 3.4653892E-05 | 1.6843291E-05 | 1.2899974E-06 | 1.75957e-05 |
| 5 | 9.0033707E-09 | 2.9081531E-09 | 2.3695501E-10 | 4.04949e-08 |
| 6 | 0 | 0 | 0 | 0 |
Paso 8: Calcule nuevas ubicaciones de reflexión cero restando el cálculo anterior de la iteración anterior de posiciones de reflexión cero.
| 1 | 0,53982509 | 0,81637641 | 0,97841993 |
| 2 | 0,52966599 | 0,80594006 | 0,97732092 |
| 3 | 0,52784896 | 0,80462559 | 0,97721185 |
| 4 | 0,52781431 | 0,80460874 | 0,97721056 |
| 5 | 0,5278143 | 0,80460874 | 0,97721056 |
| 6 | 0,5278143 | 0,80460874 | 0,97721056 |
Repita los pasos 3 a 8 hasta que se cumpla el criterio de convergencia de la aplicación, , que para este ejemplo se elige como 1.e-12. Una vez completado, la final puede construirse a partir de las posiciones de los ceros de reflexión final, +/-j0.5278143, +/-J0.80460874, +/-J0.97721056 y 0. Cuando la amplitud se normaliza de modo que , la construida se muestra a continuación.
El proceso de síntesis se puede validar haciendo una comprobación rápida de cada uno de los pasos 3 para garantizar una atenuación de 1 dB en esas frecuencias y que la atenuación de corte en también sea de 1 dB. El resumen del cálculo que se muestra a continuación valida el proceso de síntesis de ejemplo.
| -1dB | |
| -1dB | |
| -1dB | |
| -1dB |
La respuesta de frecuencia de magnitud final de la función de transferencia directa, , se muestra a continuación.

| Paso final: |
|---|
| Banda de paso de ondulación restringida del 55 % y 7 polos para |
| Banda de paso de ondulación equitativa de 1 dB |
| Escala de frecuencia lineal |
Ondulación de la banda de parada de Chebyshev II que constriñe
El diseño estándar del filtro Chebyshev inverso de paso bajo crea una banda de detención de rizado equitativo que comienza con un valor normalizado de 1 rad/seg hasta . Sin embargo, algunos requisitos de diseño no necesitan una banda de detención de rizado equitativo en las frecuencias altas. Un filtro Chebyshev inverso de rizado equitativo completo estándar para esta aplicación daría como resultado un filtro sobredimensionado. Restringir el rizado equitativo a un porcentaje definido de la banda de detención crea un diseño más eficiente, reduciendo el tamaño del filtro y eliminando potencialmente uno o dos componentes, lo que es útil para maximizar la eficiencia del espacio en la placa y minimizar los costos de producción para artículos fabricados en masa. [9]
Los filtros Chebyshev inversos con ondulación de banda de rechazo restringida se sintetizan exactamente con el mismo proceso que un filtro Chebyshev inverso estándar. Un filtro Chebyshev con ondulación restringida se diseña con una α invertida , donde es la atenuación de banda de rechazo en dB, los polos y ceros del filtro Chebyshev con ondulación restringida diseñado se invierten y se establece la atenuación de corte. Dado que las ecuaciones de Chebyshev estándar no funcionan con el diseño de ondulación restringida, la atenuación de corte se debe establecer utilizando el proceso descrito en el diseño de reloj de arena elíptico .
A continuación se muestran los parámetros de dispersión |S11| y |S12| para un filtro Chebyshev inverso de ondulación restringida de 7 polos con atenuación de corte de 3 dB.

Atenuación de corte no estándar y ceros de transmisión
El ejemplo de ondulación restringida anterior se mantiene simple intencionalmente al mantener la atenuación de corte igual a la atenuación de ondulación de la banda de paso, omitiendo ceros de transmisión opcionales y utilizando un orden impar que potencialmente no requiere una modificación del orden par. Sin embargo, se pueden acomodar atenuaciones de corte no estándar calculando los valores objetivo en el paso 5 para que se desplacen con respecto al 1 requerido que existe en la frecuencia de corte de , incluyendo un denominador como parte de la constante derivada que incluye ceros de transmisión e insertando dos ceros de reflexión en lugar de uno en el original en el paso 2.
Al incluir los ceros de transmisión de la banda de rechazo, es importante recordar que las raíces de incluirán los máximos de la banda de rechazo con . Estas raíces no deben incluirse en los mínimos de la banda de paso utilizados en los cálculos.
Dado que se puede utilizar para establecer la atenuación de corte en , los valores objetivo del paso 5 se pueden realizar con respecto a 1. Los valores objetivo en el paso 5 se pueden calcular utilizando la expresión para obtenible a partir de las ecuaciones anteriores.
Considere un diseño de filtro de % de constricción = 55, orden = 8, transmisión única cero en 1,1, atenuación de ondulación de banda de paso = 0,043648054 (equivalente a S12 = 20 dB de atenuación basada en la relación para redes sin pérdidas [12] ) y atenuación de corte de banda de paso = 20 dB.
El valor objetivo en el paso 5 es .01010101, y el valor a calcular es 99. Una vez completado, los polinomios característicos , , y la función de transferencia directa, , se muestran a continuación.
La validación consiste en calcular los parámetros de dispersión ( y respectivamente) para la frecuencia de constricción, la frecuencia de corte, las frecuencias mínimas de banda de paso restantes entre ellas y la frecuencia cero de transmisión como se muestra a continuación.
| -0,043648054 dB | -20dB | |
| -0,043648054 dB | -20dB | |
| -0,043648054 dB | -20dB | |
| -20dB | -0,043648054 dB | |
| - | 0 dB |
La respuesta de frecuencia de magnitud final se muestra a continuación.

| Paso final: |
|---|
| Banda de paso de ondulación restringida al 55 % y 8 polos para |
| Banda de paso de ondulación equitativa S11 de 20 dB |
| transmisión finita cero a 1,1 rad/seg |
| Atenuación de corte S12 no estándar a 20 dB |
| Escala de frecuencia geométrica |
Véase también
- Filtro de Bessel
- Filtro Butterworth
- Nodos de Chebyshev
- Polinomio de Chebyshev
- Filtro de peine
- Filtro elíptico
- Diseño de filtros
Referencias
- ^ Daniels, Richard W. (1974). Métodos de aproximación para el diseño de filtros electrónicos . Nueva York: McGraw-Hill. ISBN 0-07-015308-6.
- ^ Lutovac, Miroslav D.; Lutovac, D.; Tošić, Dejan V.; Evans, Brian Lawrence (2001). Diseño de filtros para procesamiento de señales utilizando MATLAB y Mathematica. Prentice Hall. ISBN 9780201361308.
- ^ Weinberg, Louis; Slepian, Paul (junio de 1960). "Resultados de Takahasi sobre redes en escalera de Tchebycheff y Butterworth". IRE Transactions on Circuit Theory . 7 (2): 88–101. doi :10.1109/TCT.1960.1086643.
- ^ Williams, Arthur B.; Taylors, Fred J. (1988). Manual de diseño de filtros electrónicos . Nueva York: McGraw-Hill. ISBN 0-07-070434-1.
- ^ abcd Saal, Rudolf (enero de 1979). Manual de diseño de filtros (en inglés y alemán) (1ª ed.). Múnich, Alemania: Allgemeine Elektricitais-Gesellschaft. págs.25, 26, 56–61, 116, 117. ISBN 3-87087-070-2.
- ^ Paarmann, Larry D. (2001). Diseño y análisis de filtros analógicos: una perspectiva de procesamiento de señales. Norwell, Massachusetts, EE. UU.: Kluwer Academic Publishers. pp. 137, 138. ISBN 0-7923-7373-1.
- ^ Paarmann, Larry D. (2001). Diseño y análisis de filtros analógicos: una perspectiva de procesamiento de señales. Norwell, Massachusetts, EE. UU.: Kluwer Academic Publishers. pp. 161, 162. ISBN 0-7923-7373-1.
- ^ Matthaei, George L.; Young, Leo; Jones, EMT (1980). Filtros de microondas, redes de adaptación de impedancia y estructuras de acoplamiento . Norwood, MA: Artech House. ISBN 0-89-006099-1.
- ^ abc Pelz, Dieter (2005). "Filtros de paso bajo de microondas con una banda de paso de ondulación equitativa restringida" (PDF) . AMW . 13 (7): 28 a 34 – vía APPLIED MICROWAVE & WIRELESS.
- ^ abcde Notas de la clase sobre diseño de filtros del Dr. Byron Bennett, 1985, Universidad Estatal de Montana, Departamento de Ingeniería Eléctrica, Bozeman , Montana, EE. UU.
- ^ ab Sedra, Adel S.; Brackett, Peter O. (1978). Teoría y diseño de filtros: activos y pasivos. Beaverton, Oegon, EE. UU.: Matrix Publishers, Inc., págs. 45-73. ISBN 978-0916460143.
- ^ Matthaei, George L.; Young, Leo; Jones, EMT (1984). Filtros de microondas, redes de adaptación de impudencia y estructuras de acoplamiento. 610 Washington Street, Dedham, Massachusetts, EE. UU.: Artech House, Inc. (publicado en 1985). pág. 44. ISBN 0-89006-099-1.
{{cite book}}: CS1 maint: location (link)









































![{\displaystyle P'=\left[{\sqrt {\left({\frac {P^{2}+cos^{2}{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}}{1-{cos^{2}{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}}}}\right)}}\right]_{\text{Semiplano izquierdo}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16d85b6994fd30599cdefbbebe97d4d04fc99623)
![{\displaystyle n=ceil{\bigg [}{\frac {\cosh ^{-1}{\sqrt {\frac {10^{\alpha _{s}/10}-1}{10^{\alpha _{p}/10}-1}}}}{\cosh ^{-1}{(\omega _{s}/\omega _{p})}}}{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70577ff1ae5804a8bbbe75fa1fb842e4030b4adf)









































![{\displaystyle \beta =\ln \left[\coth \left({\frac {\delta }{17.37}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/510d0b303b2f5a1fb8e4ec4aafaa780908223ec9)
















![{\displaystyle {\begin{aligned}&B=\prod _{i=1}^{N}(M_{i}s+1)\\&K(s)_{num}=\sum _{i=N}^{i\geq 0{\text{, paso }}=-2}{\bigg [}\sum _{j=i}^{j\geq 0{\text{, paso }}=-2}B_{j}{\binom {(Nj)/2}{(Ni)/2}}{\bigg ]}s^{i}\\&N={\text{ orden del filtro de Chebyshev}}\\&B={\text{ un polinomio creado por el producto de los factores especificados}}\\&B_{j}={\text{ el }}j_{ésimo}{\text{ coeficiente de orden del polinomio }}B\\&{\binom {n}{k}}{\text{ es el función de coeficiente binomial}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a3702f6e682475c1465d6bd8144a02f0f3b5c77)

















































![{\displaystyle {\begin{aligned}&[B_{k}]={\begin{bmatrix}|K(j\omega _{1})_{|K(j)|=1}|-1\\|K(j\omega _{2})_{|K(j)|=1}|-1\\\vdots \\|K(j\omega _{N_{Rz}})_{|K(j)|=1}|-1\\\end{bmatrix}}\\&\\&[J(R_{k},\omega _{i})][\Delta _{k}]=[B_{k}]\\&\\&[Rz_{k+1}]=[Rz_{k}]+[\Delta _{k}]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d39e112491de61de26542a660d170b37916368f)























![{\displaystyle [\Delta _{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6441738822de8bac7eb3f8d38b2f9083bf44f823)
![{\displaystyle [J(R_{k},\omega _{i})][\Delta _{k}]=[B_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a30891bad690af45f8fe4b04230804be590ef930)



![{\estilo de visualización [\Delta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c72f4d90ef418b5b2e91f343208ef0d36587d3df)
![{\displaystyle [Rz_{k}]_{\text{siguiente}}=[Rz_{k}]-[\Delta z_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebdd13ac745c12b5b779f462fd190a1b054a0d06)



































