Función de una variable real

En el análisis matemático y en aplicaciones en geometría , matemáticas aplicadas , ingeniería y ciencias naturales , una función de una variable real es una función cuyo dominio son los números reales , o un subconjunto de los mismos que contiene un intervalo de longitud positiva. La mayoría de las funciones reales que se consideran y estudian son diferenciables en algún intervalo. Las funciones de este tipo más ampliamente consideradas son las funciones reales , que son las funciones de valor real de una variable real, es decir, las funciones de una variable real cuyo codominio es el conjunto de números reales.${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {R}}$

Sin embargo, el codominio de una función de una variable real puede ser cualquier conjunto. Sin embargo, a menudo se supone que tiene una estructura de - espacio vectorial sobre los reales. Es decir, el codominio puede ser un espacio euclidiano , un vector de coordenadas , el conjunto de matrices de números reales de un tamaño dado, o un - álgebra , como los números complejos o los cuaterniones . La estructura - espacio vectorial del codominio induce una estructura de - espacio vectorial sobre las funciones. Si el codominio tiene una estructura de - álgebra, lo mismo es cierto para las funciones.${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {R}}$

La imagen de una función de una variable real es una curva en el codominio. En este contexto, una función que define una curva se denomina ecuación paramétrica de la curva.

Cuando el codominio de una función de una variable real es un espacio vectorial de dimensión finita , la función puede considerarse como una secuencia de funciones reales. Esto se utiliza a menudo en aplicaciones.

Una función real es una función de un subconjunto de a donde denota como es habitual el conjunto de números reales . Es decir, el dominio de una función real es un subconjunto , y su codominio es . Generalmente se supone que el dominio contiene un intervalo de longitud positiva.${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {R} ,}$${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {R} .}$

En el caso de muchas funciones reales de uso común, el dominio es el conjunto de números reales y la función es continua y diferenciable en todos los puntos del dominio. Se dice que estas funciones están definidas, son continuas y diferenciables en todas partes. Este es el caso de:

• Todas las funciones polinómicas , incluidas las funciones constantes y las funciones lineales.
• Funciones seno y coseno
• Función exponencial

Algunas funciones están definidas en todas partes, pero no son continuas en algunos puntos. Por ejemplo

• La función escalonada de Heaviside está definida en todas partes, pero no es continua en cero.

Algunas funciones están definidas y son continuas en todas partes, pero no son diferenciables en todas partes. Por ejemplo

• El valor absoluto está definido y es continuo en todas partes, y es diferenciable en todas partes, excepto en cero.
• La raíz cúbica está definida y es continua en todas partes, y es diferenciable en todas partes, excepto en cero.

Muchas funciones comunes no están definidas en todas partes, pero son continuas y diferenciables en todos los lugares donde están definidas. Por ejemplo:

• Una función racional es un cociente de dos funciones polinómicas y no está definida en los ceros del denominador.
• La función tangente no está definida para donde k es cualquier entero.${\displaystyle {\frac {\pi }{2}}+k\pi ,}$
• La función logaritmo se define solo para valores positivos de la variable.

Algunas funciones son continuas en todo su dominio y no diferenciables en algunos puntos. Este es el caso de:

• La raíz cuadrada se define solo para valores no negativos de la variable y no es diferenciable en 0 (es diferenciable para todos los valores positivos de la variable).

Una función de valor real de una variable real es una función que toma como entrada un número real , comúnmente representado por la variable x , para producir otro número real, el valor de la función, comúnmente denotado f ( x ). Para simplificar, en este artículo una función de valor real de una variable real se llamará simplemente función . Para evitar cualquier ambigüedad, se especificarán explícitamente los otros tipos de funciones que pueden ocurrir.

Algunas funciones están definidas para todos los valores reales de las variables (se dice que están definidas en todas partes), pero otras funciones están definidas sólo si el valor de la variable se toma en un subconjunto X de , el dominio de la función, que siempre se supone que contiene un intervalo de longitud positiva. En otras palabras, una función de valor real de una variable real es una función${\displaystyle \mathbb {R}}$

${\displaystyle f:X\to \mathbb {R}}$

tal que su dominio X es un subconjunto de que contiene un intervalo de longitud positiva.${\displaystyle \mathbb {R}}$

Un ejemplo simple de una función en una variable podría ser:

${\displaystyle f:X\to \mathbb {R}}$

${\displaystyle X=\{x\en \mathbb {R} \,:\,x\geq 0\}}$

${\displaystyle f(x)={\sqrt {x}}}$

cual es la raíz cuadrada de x .

La imagen de una función es el conjunto de todos los valores de f cuando la variable x se encuentra en todo el dominio de f . En el caso de una función continua (ver más abajo la definición) de valor real con un dominio conexo, la imagen es un intervalo o un valor único. En este último caso, la función es una función constante .${\estilo de visualización f(x)}$

La preimagen de un número real dado y es el conjunto de las soluciones de la ecuación y = f ( x ) .

El dominio de una función de varias variables reales es un subconjunto de que a veces se define explícitamente. De hecho, si se restringe el dominio X de una función f a un subconjunto Y ⊂ X , se obtiene formalmente una función diferente, la restricción de f a Y , que se denota f _{| Y} . En la práctica, a menudo no es perjudicial identificar f y f _{| Y} , y omitir el subíndice _{| Y} .${\displaystyle \mathbb {R}}$

Por el contrario, a veces es posible ampliar de forma natural el dominio de una función dada, por ejemplo mediante continuidad o por continuación analítica . Esto significa que no conviene definir explícitamente el dominio de una función de variable real.

Las operaciones aritméticas se pueden aplicar a las funciones de la siguiente manera:

• Para cada número real r , la función constante , está definida en todas partes.${\displaystyle (x)\mapsto r}$
• Para cada número real r y cada función f , la función tiene el mismo dominio que f (o está definida en todas partes si r = 0).${\displaystyle rf:(x)\mapsto rf(x)}$
• Si f y g son dos funciones de dominios respectivos X e Y tales que X ∩ Y contiene un subconjunto abierto de , entonces y son funciones que tienen un dominio que contiene X ∩ Y .${\displaystyle \mathbb {R}}$${\displaystyle f+g:(x)\mapsto f(x)+g(x)}$${\displaystyle f\,g:(x)\mapsto f(x)\,g(x)}$

De ello se deduce que las funciones de n variables que están definidas en todas partes y las funciones de n variables que están definidas en alguna vecindad de un punto dado forman ambas álgebras conmutativas sobre los números reales ( -álgebras).${\displaystyle \mathbb {R}}$

De manera similar, se puede definir que es una función solo si el conjunto de los puntos ( x ) en el dominio de f tales que f ( x ) ≠ 0 contiene un subconjunto abierto de . Esta restricción implica que las dos álgebras anteriores no son cuerpos .${\displaystyle 1/f:(x)\mapsto 1/f(x),}$${\displaystyle \mathbb {R}}$

Hasta la segunda mitad del siglo XIX, los matemáticos sólo consideraban funciones continuas . En aquella época, el concepto de continuidad se había elaborado para las funciones de una o varias variables reales mucho antes de que se definieran formalmente los espacios topológicos y las funciones continuas entre espacios topológicos. Como las funciones continuas de una variable real son omnipresentes en las matemáticas, conviene definir este concepto sin hacer referencia al concepto general de funciones continuas entre espacios topológicos.

Para definir la continuidad, es útil considerar la función de distancia de , que es una función definida en todas partes de 2 variables reales:${\displaystyle \mathbb {R}}$${\displaystyle d(x,y)=|xy|}$

Una función f es continua en un punto interior a su dominio, si, para cada número real positivo ε , existe un número real positivo φ tal que para todos tales que En otras palabras, φ puede elegirse lo suficientemente pequeño para tener la imagen por f del intervalo de radio φ centrado en contenido en el intervalo de longitud 2 ε centrado en Una función es continua si es continua en cada punto de su dominio.${\estilo de visualización a}$${\displaystyle |f(x)-f(a)|<\varepsilon }$${\displaystyle x}$${\displaystyle d(x,a)<\varphi .}$${\displaystyle a}$${\displaystyle f(a).}$

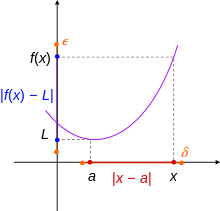
El límite de una función de valor real de una variable real es el siguiente. ^[1] Sea a un punto en el cierre topológico del dominio X de la función f . La función f tiene un límite L cuando x tiende hacia a , denotado

${\displaystyle L=\lim _{x\to a}f(x),}$

si se cumple la siguiente condición: Para cada número real positivo ε > 0, existe un número real positivo δ > 0 tal que

${\displaystyle |f(x)-L|<\varepsilon }$

para todo x en el dominio tal que

${\displaystyle d(x,a)<\delta .}$

Si el límite existe, es único. Si a está en el interior del dominio, el límite existe si y sólo si la función es continua en a . En este caso, tenemos

${\displaystyle f(a)=\lim _{x\to a}f(x).}$

Cuando a está en el límite del dominio de f , y si f tiene un límite en a , la última fórmula permite "extender por continuidad" el dominio de f hasta a .

Se pueden recopilar varias funciones cada una de una variable real, digamos

${\displaystyle y_{1}=f_{1}(x)\,,\quad y_{2}=f_{2}(x)\,,\ldots ,y_{n}=f_{n}(x)}$

en un vector parametrizado por x :

${\displaystyle \mathbf {y} =(y_{1},y_{2},\ldots ,y_{n})=[f_{1}(x),f_{2}(x),\ldots ,f_{n}(x)]}$

La derivada del vector y es la derivada vectorial de f _i ( x ) para i = 1, 2, ..., n :

${\displaystyle {\frac {d\mathbf {y} }{dx}}=\left({\frac {dy_{1}}{dx}},{\frac {dy_{2}}{dx}},\ldots ,{\frac {dy_{n}}{dx}}\right)}$

También se pueden realizar integrales de línea a lo largo de una curva espacial parametrizada por x , con vector de posición r = r ( x ), integrando con respecto a la variable x :

${\displaystyle \int _{a}^{b}\mathbf {y} (x)\cdot d\mathbf {r} =\int _{a}^{b}\mathbf {y} (x)\cdot {\frac {d\mathbf {r} (x)}{dx}}dx}$

donde · es el producto escalar , y x = a y x = b son los puntos inicial y final de la curva.

Con las definiciones de integración y derivadas, se pueden formular teoremas clave, entre ellos el teorema fundamental del cálculo , el de integración por partes y el teorema de Taylor . La evaluación de una mezcla de integrales y derivadas se puede realizar mediante la diferenciación de teoremas bajo el signo de la integral .

Una función implícita de valor real de una variable real no se escribe en la forma " y = f ( x )". En cambio, la aplicación es del espacio ² al elemento cero en (solo el cero ordinario 0):${\displaystyle \mathbb {R} }$${\displaystyle \mathbb {R} }$

${\displaystyle \phi :\mathbb {R} ^{2}\to \{0\}}$

y

${\displaystyle \phi (x,y)=0}$

es una ecuación en las variables. Las funciones implícitas son una forma más general de representar funciones, ya que si:

${\displaystyle y=f(x)}$

entonces siempre podemos definir:

${\displaystyle \phi (x,y)=y-f(x)=0}$

pero lo inverso no siempre es posible, es decir, no todas las funciones implícitas tienen la forma de esta ecuación.

Dadas las funciones r ₁ = r ₁ ( t ) , r ₂ = r ₂ ( t ) , ..., r _n = r _n ( t ) todas de una variable común t , de modo que:

${\displaystyle {\begin{aligned}r_{1}:\mathbb {R} \rightarrow \mathbb {R} &\quad r_{2}:\mathbb {R} \rightarrow \mathbb {R} &\cdots &\quad r_{n}:\mathbb {R} \rightarrow \mathbb {R} \\r_{1}=r_{1}(t)&\quad r_{2}=r_{2}(t)&\cdots &\quad r_{n}=r_{n}(t)\\\end{aligned}}}$

o tomados en conjunto:

${\displaystyle \mathbf {r} :\mathbb {R} \rightarrow \mathbb {R} ^{n}\,,\quad \mathbf {r} =\mathbf {r} (t)}$

entonces la n -tupla parametrizada,

${\displaystyle \mathbf {r} (t)=[r_{1}(t),r_{2}(t),\ldots ,r_{n}(t)]}$

describe una curva espacial unidimensional .

En un punto r ( t = c ) = a = ( a ₁ , a ₂ , ..., a _n ) para alguna constante t = c , las ecuaciones de la línea tangente unidimensional a la curva en ese punto se dan en términos de las derivadas ordinarias de r ₁ ( t ), r ₂ ( t ), ..., r _n ( t ) y r con respecto a t :

${\displaystyle {\frac {r_{1}(t)-a_{1}}{dr_{1}(t)/dt}}={\frac {r_{2}(t)-a_{2}}{dr_{2}(t)/dt}}=\cdots ={\frac {r_{n}(t)-a_{n}}{dr_{n}(t)/dt}}}$

La ecuación del hiperplano n -dimensional normal a la línea tangente en r = a es:

${\displaystyle (p_{1}-a_{1}){\frac {dr_{1}(t)}{dt}}+(p_{2}-a_{2}){\frac {dr_{2}(t)}{dt}}+\cdots +(p_{n}-a_{n}){\frac {dr_{n}(t)}{dt}}=0}$

o en términos del producto escalar :

${\displaystyle (\mathbf {p} -\mathbf {a} )\cdot {\frac {d\mathbf {r} (t)}{dt}}=0}$

donde p = ( p ₁ , p ₂ , ..., p _n ) son puntos en el plano , no en la curva espacial.

La interpretación física y geométrica de d r ( t )/ dt es la " velocidad " de una partícula puntual que se mueve a lo largo de la trayectoria r ( t ), tratando r como las coordenadas del vector de posición espacial parametrizadas por el tiempo t , y es un vector tangente a la curva espacial para todo t en la dirección instantánea de movimiento. En t = c , la curva espacial tiene un vector tangente d r ( t )/ dt | _{t = c} , y el hiperplano normal a la curva espacial en t = c también es normal a la tangente en t = c . Cualquier vector en este plano ( p − a ) debe ser normal a d r ( t )/ dt | _{t = c} .

De manera similar, d ² r ( t )/ dt ² es la " aceleración " de la partícula, y es un vector normal a la curva dirigida a lo largo del radio de curvatura .

Una matriz también puede ser función de una sola variable. Por ejemplo, la matriz de rotación en 2D:

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}}$

es una función matricial del ángulo de rotación de respecto al origen. De manera similar, en la relatividad especial , la matriz de transformación de Lorentz para un impulso puro (sin rotaciones):

${\displaystyle \Lambda (\beta )={\begin{bmatrix}{\frac {1}{\sqrt {1-\beta ^{2}}}}&-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&0&0\\-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&{\frac {1}{\sqrt {1-\beta ^{2}}}}&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}}$

es una función del parámetro de impulso β = v / c , en el que v es la velocidad relativa entre los marcos de referencia (una variable continua), y c es la velocidad de la luz , una constante.

Generalizando la sección anterior, la salida de una función de una variable real también puede estar en un espacio de Banach o en un espacio de Hilbert . En estos espacios, la división, la multiplicación y los límites están definidos, por lo que nociones como derivada e integral siguen siendo válidas. Esto ocurre especialmente a menudo en mecánica cuántica, donde se toma la derivada de un ket o de un operador . Esto ocurre, por ejemplo, en la ecuación general de Schrödinger dependiente del tiempo :

${\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi ={\hat {H}}\Psi }$

donde se toma la derivada de una función de onda, que puede ser un elemento de varios espacios de Hilbert diferentes.

Una función de valor complejo de una variable real puede definirse relajando, en la definición de las funciones de valor real, la restricción del codominio a los números reales y permitiendo valores complejos .

Si f ( x ) es una función de valor complejo, se puede descomponer como

f ( x ) = g ( x ) + ih ( x ) ,

donde g y h son funciones de valores reales. En otras palabras, el estudio de las funciones de valores complejos se reduce fácilmente al estudio de pares de funciones de valores reales.

La cardinalidad del conjunto de funciones de valor real de una variable real, , es , que es estrictamente mayor que la cardinalidad del continuo (es decir, el conjunto de todos los números reales). Este hecho se verifica fácilmente mediante aritmética cardinal:${\displaystyle \mathbb {R} ^{\mathbb {R} }=\{f:\mathbb {R} \to \mathbb {R} \}}$${\displaystyle \beth _{2}=2^{\mathfrak {c}}}$

$${\displaystyle \mathrm {card} (\mathbb {R} ^{\mathbb {R} })=\mathrm {card} (\mathbb {R} )^{\mathrm {card} (\mathbb {R} )}={\mathfrak {c}}^{\mathfrak {c}}=(2^{\aleph _{0}})^{\mathfrak {c}}=2^{\aleph _{0}\cdot {\mathfrak {c}}}=2^{\mathfrak {c}}.}$$

Además, si es un conjunto tal que , entonces la cardinalidad del conjunto también es , ya que${\displaystyle X}$${\displaystyle 2\leq \mathrm {card} (X)\leq {\mathfrak {c}}}$${\displaystyle X^{\mathbb {R} }=\{f:\mathbb {R} \to X\}}$${\displaystyle 2^{\mathfrak {c}}}$

$${\displaystyle 2^{\mathfrak {c}}=\mathrm {card} (2^{\mathbb {R} })\leq \mathrm {card} (X^{\mathbb {R} })\leq \mathrm {card} (\mathbb {R} ^{\mathbb {R} })=2^{\mathfrak {c}}.}$$

Sin embargo, el conjunto de funciones continuas tiene una cardinalidad estrictamente menor, la cardinalidad del continuo, . Esto se deduce del hecho de que una función continua está completamente determinada por su valor en un subconjunto denso de su dominio. ^[2] Por lo tanto, la cardinalidad del conjunto de funciones continuas de valores reales en los números reales no es mayor que la cardinalidad del conjunto de funciones de valores reales de una variable racional. Por aritmética cardinal:${\displaystyle C^{0}(\mathbb {R} )=\{f:\mathbb {R} \to \mathbb {R} :f\ \mathrm {continuous} \}}$${\displaystyle {\mathfrak {c}}}$

$${\displaystyle \mathrm {card} (C^{0}(\mathbb {R} ))\leq \mathrm {card} (\mathbb {R} ^{\mathbb {Q} })=(2^{\aleph _{0}})^{\aleph _{0}}=2^{\aleph _{0}\cdot \aleph _{0}}=2^{\aleph _{0}}={\mathfrak {c}}.}$$

Por otra parte, dado que hay una clara biyección entre y el conjunto de funciones constantes , que forma un subconjunto de , también debe cumplirse. Por lo tanto, .${\displaystyle \mathbb {R} }$${\displaystyle \{f:\mathbb {R} \to \mathbb {R} :f(x)\equiv x_{0}\}}$${\displaystyle C^{0}(\mathbb {R} )}$${\displaystyle \mathrm {card} (C^{0}(\mathbb {R} ))\geq {\mathfrak {c}}}$${\displaystyle \mathrm {card} (C^{0}(\mathbb {R} ))={\mathfrak {c}}}$

• Análisis real
• Función de varias variables reales
• Análisis complejo
• Función de varias variables complejas

• F. Ayres, E. Mendelson (2009). Cálculo . Serie de esquemas de Schaum (quinta edición). McGraw Hill. ISBN 978-0-07-150861-2.
• R. Wrede, MR Spiegel (2010). Cálculo avanzado . Serie de esquemas de Schaum (3.ª ed.). McGraw Hill. ISBN 978-0-07-162366-7.
• N. Bourbaki (2004). Funciones de una variable real: teoría elemental. Springer. ISBN 354-065-340-6.

• Cálculo multivariable
• LA Talman (2007) Diferenciabilidad para funciones multivariables