Estadística de pedidos

En estadística , la estadística de orden k de una muestra estadística es igual a su valor k más pequeño. ^[1] Junto con las estadísticas de rango , las estadísticas de orden se encuentran entre las herramientas más fundamentales en la estadística no paramétrica y la inferencia .

Los casos especiales importantes de las estadísticas de orden son el valor mínimo y máximo de una muestra y (con algunas salvedades que se analizan a continuación) la mediana de la muestra y otros cuartiles de la muestra .

Cuando se utiliza la teoría de probabilidad para analizar las estadísticas de orden de muestras aleatorias de una distribución continua , se utiliza la función de distribución acumulativa para reducir el análisis al caso de las estadísticas de orden de la distribución uniforme .

Por ejemplo, supongamos que se observan o registran cuatro números, lo que da como resultado una muestra de tamaño 4. Si los valores de la muestra son

6, 9, 3, 7,

Las estadísticas del pedido se indicarían

${\displaystyle x_{(1)}=3,\ \ x_{(2)}=6,\ \ x_{(3)}=7,\ \ x_{(4)}=9,\,}$

donde el subíndice ( i ) entre paréntesis indica el estadístico de orden i de la muestra.

La estadística de primer orden (o estadística de orden más pequeño ) es siempre el mínimo de la muestra, es decir,

${\displaystyle X_{(1)}=\min\{\,X_{1},\ldots ,X_{n}\,\}}$

donde, siguiendo una convención común, utilizamos letras mayúsculas para referirnos a variables aleatorias y letras minúsculas (como arriba) para referirnos a sus valores reales observados.

De manera similar, para una muestra de tamaño n , el estadístico de orden n (o estadístico de orden más grande ) es el máximo , es decir,

${\displaystyle X_{(n)}=\max\{\,X_{1},\ldots ,X_{n}\,\}.}$

El rango de muestra es la diferencia entre el máximo y el mínimo. Es una función de las estadísticas de orden:

${\displaystyle {\rm {Rango}}\{\,X_{1},\ldots ,X_{n}\,\}=X_{(n)}-X_{(1)}.}$

Una estadística importante similar en el análisis de datos exploratorios que está simplemente relacionada con las estadísticas de orden es el rango intercuartil de la muestra .

La mediana de la muestra puede ser o no un estadístico de orden, ya que hay un único valor medio solo cuando el número n de observaciones es impar . Más precisamente, si n = 2 m +1 para algún entero m , entonces la mediana de la muestra es y, por lo tanto, es un estadístico de orden. Por otro lado, cuando n es par , n = 2 m y hay dos valores medios, y , y la mediana de la muestra es alguna función de los dos (generalmente el promedio) y, por lo tanto, no es un estadístico de orden. Observaciones similares se aplican a todos los cuantiles de la muestra.$Estilo de visualización X_{(m+1)}}$$Estilo de visualización X_{(m)}}$$Estilo de visualización X_{(m+1)}}$

Dadas cualesquiera variables aleatorias X ₁ , X ₂ , ..., X _n , las estadísticas de orden X ₍₁₎ , X ₍₂₎ , ..., X _{( n )} también son variables aleatorias, definidas al ordenar los valores ( realizaciones ) de X ₁ , ..., X _n en orden creciente.

Cuando las variables aleatorias X ₁ , X ₂ , ..., X _n forman una muestra son independientes y se distribuyen de forma idéntica . Este es el caso que se trata a continuación. En general, las variables aleatorias X ₁ , ..., X _n pueden surgir al muestrear más de una población. Entonces son independientes , pero no necesariamente se distribuyen de forma idéntica, y su distribución de probabilidad conjunta viene dada por el teorema de Bapat–Beg .

A partir de ahora, supondremos que las variables aleatorias en consideración son continuas y, cuando sea conveniente, supondremos también que tienen una función de densidad de probabilidad (PDF), es decir, que son absolutamente continuas . Las peculiaridades del análisis de distribuciones que asignan masa a puntos (en particular, distribuciones discretas ) se discuten al final.

Para una muestra aleatoria como la anterior, con distribución acumulativa , las estadísticas de orden para esa muestra tienen distribuciones acumulativas como las siguientes ^[2] (donde r especifica qué estadística de orden):$Estilo de visualización F_{X}(x)}$

${\displaystyle F_{X_{(r)}}(x)=\sum _{j=r}^{n}{\binom {n}{j}}[F_{X}(x)]^{j }[1-F_{X}(x)]^{nj}}$

La función de densidad de probabilidad correspondiente se puede derivar de este resultado, y se encuentra que es

${\displaystyle f_{X_{(r)}}(x)={\frac {n!}{(r-1)!(nr)!}}f_{X}(x)[F_{X}(x)]^{r-1}[1-F_{X}(x)]^{nr}.}$

Además, hay dos casos especiales, que tienen CDF que son fáciles de calcular.

${\displaystyle F_{X_{(n)}}(x)=\operatorname {Prob} (\max\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=[F_{X}(x)]^{n}}$

${\displaystyle F_{X_{(1)}}(x)=\operatorname {Prob} (\min\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=1-[1-F_{X}(x)]^{n}}$

Lo cual puede deducirse mediante una cuidadosa consideración de las probabilidades.

En esta sección mostramos que las estadísticas de orden de la distribución uniforme en el intervalo unitario tienen distribuciones marginales que pertenecen a la familia de distribuciones beta . También proporcionamos un método simple para derivar la distribución conjunta de cualquier número de estadísticas de orden y, finalmente, traducimos estos resultados a distribuciones continuas arbitrarias utilizando la función de distribución acumulativa (cdf) .

En esta sección asumimos que se trata de una muestra aleatoria extraída de una distribución continua con función de distribución acumulativa . Denotando que obtenemos la muestra aleatoria correspondiente de la distribución uniforme estándar . Nótese que las estadísticas de orden también satisfacen .${\displaystyle X_{1},X_{2},\ldots ,X_{n}}$$Estilo de visualización F_ {X}}$${\displaystyle U_{i}=F_{X}(X_{i})}$${\displaystyle U_{1},\ldots ,U_{n}}$${\displaystyle U_{(i)}=F_{X}(X_{(i)})}$

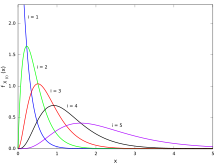
La función de densidad de probabilidad de la estadística de orden es igual a ^[3]${\displaystyle U_{(k)}}$

${\displaystyle f_{U_{(k)}}(u)={n! \sobre (k-1)!(nk)!}u^{k-1}(1-u)^{nk}}$

Es decir, la estadística de orden k de la distribución uniforme es una variable aleatoria distribuida en beta . ^{[3] [4]}

${\displaystyle U_{(k)}\sim \operatorname {Beta} (k,n+1\mathbf {-} k).}$

La prueba de estas afirmaciones es la siguiente. Para que u esté entre u y u  +  du , es necesario que exactamente k  − 1 elementos de la muestra sean menores que u , y que al menos uno esté entre u y u  + d u . La probabilidad de que más de uno esté en este último intervalo ya es , por lo que tenemos que calcular la probabilidad de que exactamente k  − 1, 1 y n  −  k observaciones caigan en los intervalos , y respectivamente. Esto es igual a (consulte la distribución multinomial para obtener más detalles)${\displaystyle U_{(k)}}$${\displaystyle O(du^{2})}$${\estilo de visualización (0,u)}$${\displaystyle (u,u+du)}$${\displaystyle (u+du,1)}$

${\displaystyle {n! \over (k-1)!(nk)!}u^{k-1}\cdot du\cdot (1-u-du)^{nk}}$

y el resultado sigue.

La media de esta distribución es k / ( n + 1).

De manera similar, para i  <  j , se puede demostrar que la función de densidad de probabilidad conjunta de las dos estadísticas de orden U _{( i )}  <  U _{( j ) es}

${\displaystyle f_{U_{(i)},U_{(j)}}(u,v)=n!{u^{i-1} \over (i-1)!}{(vu)^{ ji-1} \sobre (ji-1)!}{(1-v)^{nj} \sobre (nj)!}}$

que es (hasta términos de orden superior a ) la probabilidad de que i  − 1, 1, j  − 1 −  i , 1 y n  −  j elementos de muestra caigan en los intervalos , , , , respectivamente.${\displaystyle O(du\,dv)}$${\estilo de visualización (0,u)}$${\displaystyle (u,u+du)}$${\estilo de visualización (u+du,v)}$${\estilo de visualización (v,v+dv)}$${\estilo de visualización (v+dv,1)}$

Se razona de una manera completamente análoga para derivar las distribuciones conjuntas de orden superior. Tal vez sea sorprendente que la densidad conjunta de las estadísticas de orden n resulte constante :

${\displaystyle f_{U_{(1)},U_{(2)},\ldots ,U_{(n)}}(u_{1},u_{2},\ldots ,u_{n})=n!.}$

Una forma de entender esto es que la muestra no ordenada tiene una densidad constante igual a 1, y que hay n ! permutaciones diferentes de la muestra correspondientes a la misma secuencia de estadísticas de orden. Esto está relacionado con el hecho de que 1/ n ! es el volumen de la región . También está relacionado con otra particularidad de las estadísticas de orden de las variables aleatorias uniformes: de la desigualdad BRS se deduce que el número máximo esperado de variables aleatorias uniformes U(0,1] que se pueden elegir de una muestra de tamaño n con una suma que no exceda de está acotado por encima de , que es, por tanto, invariante en el conjunto de todas con producto constante .${\displaystyle 0<u_{1}<\cdots <u_{n}<1}$${\displaystyle 0<s<n/2}$${\displaystyle {\sqrt {2sn}}}$${\estilo de visualización s,n}$${\estilo de visualización sn}$

Utilizando las fórmulas anteriores, se puede derivar la distribución del rango de las estadísticas de orden, es decir, la distribución de , es decir, el máximo menos el mínimo. De manera más general, para , también tiene una distribución beta: A partir de estas fórmulas podemos derivar la covarianza entre dos estadísticas de orden: La fórmula se deduce de notar que y comparar eso con donde , que es la distribución real de la diferencia.${\displaystyle U_{(n)}-U_{(1)}}$${\displaystyle n\geq k>j\geq 1}$${\displaystyle U_{(k)}-U_{(j)}}$$${\displaystyle U_{(k)}-U_{(j)}\sim \operatorname {Beta} (kj,n-(kj)+1)}$$$${\displaystyle \operatorname {Cov} (U_{(k)},U_{(j)})={\frac {j(n-k+1)}{(n+1)^{2}(n+ 2)}}}$$$${\displaystyle \operatorname {Var} (U_{(k)}-U_{(j)})=\operatorname {Var} (U_{(k)})+\operatorname {Var} (U_{(j)} )-2\cdot \operatorname {Cov} (U_{(k)},U_{(j)})={\frac {k(n-k+1)}{(n+1)^{2}( n+2)}}+{\frac {j(n-j+1)}{(n+1)^{2}(n+2)}}-2\cdot \operatorname {Cov} (U_{( k)},U_{(j)})}$$$${\displaystyle \operatorname {Var} (U)={\frac {(k-j)(n-(k-j)+1)}{(n+1)^{2}(n+2)}}}$$${\displaystyle U\sim \operatorname {Beta} (k-j,n-(k-j)+1)}$

Para una muestra aleatoria de tamaño n de una distribución exponencial con parámetro λ , las estadísticas de orden X _{( i )} para i = 1,2,3, ..., n tienen cada una distribución${\displaystyle X_{1},X_{2},..,X_{n}}$

${\displaystyle X_{(i)}{\stackrel {d}{=}}{\frac {1}{\lambda }}\left(\sum _{j=1}^{i}{\frac {Z_{j}}{n-j+1}}\right)}$

donde Z _j son variables aleatorias exponenciales estándar iid (es decir, con parámetro de tasa 1). Este resultado fue publicado por primera vez por Alfréd Rényi . ^{[5] [6]}

La transformada de Laplace de las estadísticas de orden se puede muestrear a partir de una distribución de Erlang a través de un método de conteo de trayectorias ^{[ aclaración necesaria ]} . ^[7]

Si F _X es absolutamente continua , tiene una densidad tal que , y podemos usar las sustituciones${\displaystyle dF_{X}(x)=f_{X}(x)\,dx}$

${\displaystyle u=F_{X}(x)}$

y

${\displaystyle du=f_{X}(x)\,dx}$

para derivar las siguientes funciones de densidad de probabilidad para las estadísticas de orden de una muestra de tamaño n extraída de la distribución de X :

${\displaystyle f_{X_{(k)}}(x)={\frac {n!}{(k-1)!(n-k)!}}[F_{X}(x)]^{k-1}[1-F_{X}(x)]^{n-k}f_{X}(x)}$

${\displaystyle f_{X_{(j)},X_{(k)}}(x,y)={\frac {n!}{(j-1)!(k-j-1)!(n-k)!}}[F_{X}(x)]^{j-1}[F_{X}(y)-F_{X}(x)]^{k-1-j}[1-F_{X}(y)]^{n-k}f_{X}(x)f_{X}(y)}$dónde${\displaystyle x\leq y}$

${\displaystyle f_{X_{(1)},\ldots ,X_{(n)}}(x_{1},\ldots ,x_{n})=n!f_{X}(x_{1})\cdots f_{X}(x_{n})}$dónde${\displaystyle x_{1}\leq x_{2}\leq \dots \leq x_{n}.}$

Una pregunta interesante es qué tan bien funcionan las estadísticas de orden como estimadores de los cuantiles de la distribución subyacente.

El caso más simple a considerar es qué tan bien la mediana de la muestra estima la mediana de la población.

Como ejemplo, considere una muestra aleatoria de tamaño 6. En ese caso, la mediana de la muestra se define generalmente como el punto medio del intervalo delimitado por las estadísticas de tercer y cuarto orden. Sin embargo, sabemos por la discusión anterior que la probabilidad de que este intervalo contenga realmente la mediana de la población es ^{[ aclaración necesaria ]}

${\displaystyle {6 \choose 3}(1/2)^{6}={5 \over 16}\approx 31\%.}$

Aunque la mediana de la muestra es probablemente una de las mejores estimaciones puntuales independientes de la distribución de la mediana de la población, lo que ilustra este ejemplo es que no es particularmente buena en términos absolutos. En este caso particular, un mejor intervalo de confianza para la mediana es el delimitado por las estadísticas de segundo y quinto orden, que contiene la mediana de la población con probabilidad

${\displaystyle \left[{6 \choose 2}+{6 \choose 3}+{6 \choose 4}\right](1/2)^{6}={25 \over 32}\approx 78\%.}$

Con un tamaño de muestra tan pequeño, si se desea tener al menos un 95% de confianza, se debe decir que la mediana está entre el mínimo y el máximo de las 6 observaciones con una probabilidad de 31/32 o aproximadamente el 97%. El tamaño 6 es, de hecho, el tamaño de muestra más pequeño tal que el intervalo determinado por el mínimo y el máximo es al menos un intervalo de confianza del 95% para la mediana de la población.

Para la distribución uniforme, cuando n tiende a infinito, el p ^-ésimo cuartil de muestra se distribuye normalmente de forma asintótica , ya que se aproxima mediante

${\displaystyle U_{(\lceil np\rceil )}\sim AN\left(p,{\frac {p(1-p)}{n}}\right).}$

Para una distribución general F con una densidad continua distinta de cero en F  ⁻¹ ( p ), se aplica una normalidad asintótica similar:

${\displaystyle X_{(\lceil np\rceil )}\sim AN\left(F^{-1}(p),{\frac {p(1-p)}{n[f(F^{-1}(p))]^{2}}}\right)}$

donde f es la función de densidad y F  ⁻¹ es la función cuantil asociada a F . Una de las primeras personas en mencionar y demostrar este resultado fue Frederick Mosteller en su artículo seminal de 1946. ^[8] Investigaciones posteriores condujeron en la década de 1960 a la representación de Bahadur , que proporciona información sobre los límites de error. La convergencia a la distribución normal también se cumple en un sentido más fuerte, como la convergencia en entropía relativa o la divergencia KL . ^[9]

Se puede hacer una observación interesante en el caso en que la distribución es simétrica y la mediana de la población es igual a la media de la población. En este caso, la media de la muestra , según el teorema del límite central , también se distribuye normalmente de forma asintótica, pero con una varianza σ ² /n en su lugar. Este análisis asintótico sugiere que la media supera a la mediana en casos de baja curtosis y viceversa. Por ejemplo, la mediana logra mejores intervalos de confianza para la distribución de Laplace , mientras que la media funciona mejor para X que se distribuyen normalmente.

Se puede demostrar que

${\displaystyle B(k,n+1-k)\ {\stackrel {\mathrm {d} }{=}}\ {\frac {X}{X+Y}},}$

dónde

${\displaystyle X=\sum _{i=1}^{k}Z_{i},\quad Y=\sum _{i=k+1}^{n+1}Z_{i},}$

siendo Z _i variables aleatorias exponenciales independientes distribuidas de forma idéntica con tasa 1. Dado que X / n e Y / n se distribuyen normalmente de forma asintótica mediante la CLT, nuestros resultados se obtienen mediante la aplicación del método delta .

Los momentos de la distribución para la estadística de primer orden se pueden utilizar para desarrollar un estimador de densidad no paramétrico. ^[10] Supongamos que queremos estimar la densidad en el punto . Consideremos las variables aleatorias , que son iid con función de distribución . En particular, .${\displaystyle f_{X}}$${\displaystyle x^{*}}$${\displaystyle Y_{i}=|X_{i}-x^{*}|}$${\displaystyle g_{Y}(y)=f_{X}(y+x^{*})+f_{X}(x^{*}-y)}$${\displaystyle f_{X}(x^{*})={\frac {g_{Y}(0)}{2}}}$

El valor esperado de la estadística de primer orden dada una muestra de observaciones totales da como resultado:${\displaystyle Y_{(1)}}$${\displaystyle N}$

${\displaystyle E(Y_{(1)})={\frac {1}{(N+1)g(0)}}+{\frac {1}{(N+1)(N+2)}}\int _{0}^{1}Q''(z)\delta _{N+1}(z)\,dz}$

donde es la función cuantil asociada con la distribución , y . Esta ecuación en combinación con una técnica de jackknifing se convierte en la base para el siguiente algoritmo de estimación de densidad,${\displaystyle Q}$${\displaystyle g_{Y}}$${\displaystyle \delta _{N}(z)=(N+1)(1-z)^{N}}$

 Entrada: una muestra de observaciones, puntos de evaluación de densidad, parámetro de ajuste (normalmente 1/3).${\displaystyle N}$${\displaystyle \{x_{\ell }\}_{\ell =1}^{M}}$${\displaystyle a\in (0,1)}$ Salida: densidad estimada en los puntos de evaluación.${\displaystyle \{{\hat {f}}_{\ell }\}_{\ell =1}^{M}}$

 1: Conjunto 2: Conjunto 3: Cree una matriz que contenga subconjuntos con observaciones cada uno.${\displaystyle m_{N}=\operatorname {round} (N^{1-a})}$${\displaystyle s_{N}={\frac {N}{m_{N}}}}$${\displaystyle s_{N}\times m_{N}}$${\displaystyle M_{ij}}$${\displaystyle m_{N}}$${\displaystyle s_{N}}$ 4: Cree un vector para almacenar las evaluaciones de densidad.${\displaystyle {\hat {f}}}$ 5: para  hacer 6: para hacer 7: Encuentra la distancia más cercana al punto actual dentro del subconjunto n${\displaystyle \ell =1\to M}$  ${\displaystyle k=1\to m_{N}}$ ${\displaystyle d_{\ell k}}$${\displaystyle x_{\ell }}$${\displaystyle k}$ 8: fin para 9: Calcular el promedio del subconjunto de distancias a 10: Calcular la estimación de densidad en 11: fin para 12: regresar${\displaystyle x_{\ell }:d_{\ell }=\sum _{k=1}^{m_{N}}{\frac {d_{\ell k}}{m_{N}}}}$${\displaystyle x_{\ell }:{\hat {f}}_{\ell }={\frac {1}{2(1+s_{N})d_{\ell }}}}$ ${\displaystyle {\hat {f}}}$

A diferencia de los parámetros de ajuste basados ​​en el ancho de banda/longitud para los enfoques basados ​​en histogramas y kernel , el parámetro de ajuste para el estimador de densidad basado en la estadística de orden es el tamaño de los subconjuntos de la muestra. Este estimador es más robusto que los enfoques basados ​​en histogramas y kernel; por ejemplo, las densidades como la distribución de Cauchy (que carece de momentos finitos) se pueden inferir sin la necesidad de modificaciones especializadas como los anchos de banda basados ​​en IQR . Esto se debe a que el primer momento de la estadística de orden siempre existe si el valor esperado de la distribución subyacente existe, pero lo inverso no es necesariamente cierto. ^[11]

Supongamos que hay variables aleatorias iid de una distribución discreta con función de distribución acumulativa y función de masa de probabilidad . Para encontrar las probabilidades de las estadísticas de orden, primero se necesitan tres valores, a saber:${\displaystyle X_{1},X_{2},\ldots ,X_{n}}$${\displaystyle F(x)}$ ${\displaystyle f(x)}$${\displaystyle k^{\text{th}}}$

${\displaystyle p_{1}=P(X<x)=F(x)-f(x),\ p_{2}=P(X=x)=f(x),{\text{ and }}p_{3}=P(X>x)=1-F(x).}$

La función de distribución acumulativa de la estadística de orden se puede calcular observando que${\displaystyle k^{\text{th}}}$

${\displaystyle {\begin{aligned}P(X_{(k)}\leq x)&=P({\text{there are at least }}k{\text{ observations less than or equal to }}x),\\&=P({\text{there are at most }}n-k{\text{ observations greater than }}x),\\&=\sum _{j=0}^{n-k}{n \choose j}p_{3}^{j}(p_{1}+p_{2})^{n-j}.\end{aligned}}}$

De manera similar, se da por${\displaystyle P(X_{(k)}<x)}$

${\displaystyle {\begin{aligned}P(X_{(k)}<x)&=P({\text{there are at least }}k{\text{ observations less than }}x),\\&=P({\text{there are at most }}n-k{\text{ observations greater than or equal to }}x),\\&=\sum _{j=0}^{n-k}{n \choose j}(p_{2}+p_{3})^{j}(p_{1})^{n-j}.\end{aligned}}}$

Nótese que la función de masa de probabilidad de es simplemente la diferencia de estos valores, es decir${\displaystyle X_{(k)}}$

${\displaystyle {\begin{aligned}P(X_{(k)}=x)&=P(X_{(k)}\leq x)-P(X_{(k)}<x),\\&=\sum _{j=0}^{n-k}{n \choose j}\left(p_{3}^{j}(p_{1}+p_{2})^{n-j}-(p_{2}+p_{3})^{j}(p_{1})^{n-j}\right),\\&=\sum _{j=0}^{n-k}{n \choose j}\left((1-F(x))^{j}(F(x))^{n-j}-(1-F(x)+f(x))^{j}(F(x)-f(x))^{n-j}\right).\end{aligned}}}$

El problema de calcular el k -ésimo elemento más pequeño (o más grande) de una lista se denomina problema de selección y se resuelve mediante un algoritmo de selección. Aunque este problema es difícil para listas muy grandes, se han creado algoritmos de selección sofisticados que pueden resolver este problema en un tiempo proporcional al número de elementos de la lista, incluso si la lista está totalmente desordenada. Si los datos se almacenan en ciertas estructuras de datos especializadas, este tiempo se puede reducir a O(log n ). En muchas aplicaciones se requieren todas las estadísticas de orden, en cuyo caso se puede utilizar un algoritmo de ordenación y el tiempo empleado es O( n log n ).

• Clasificación
• Diagrama de caja
• Desigualdad BRS
• Concomitante (estadística)
• Distribución de Fisher-Tippett
• Teorema de Bapat-Beg para las estadísticas de orden de variables aleatorias independientes pero no necesariamente idénticamente distribuidas
• Polinomio de Bernstein
• Estimador L : combinaciones lineales de estadísticas de orden
• Distribución por tamaño de rango
• Algoritmo de selección

• Muestra máxima y mínima
• Cuantil
• Percentil
• Décimo
• Cuartilla
• Mediana
• Significar
• Media y covarianza de la muestra

Las estadísticas de orden tienen muchas aplicaciones en áreas como la teoría de la confiabilidad, las matemáticas financieras, el análisis de supervivencia, la epidemiología, los deportes, el control de calidad, el riesgo actuarial, etc. Existe una extensa literatura dedicada a estudios sobre aplicaciones de las estadísticas de orden en estos campos.

Por ejemplo, una aplicación reciente en riesgo actuarial se puede encontrar en ^[12] , donde se proporcionan algunos principios de prima ponderada en términos de reclamaciones récord y k-ésimas reclamaciones récord.

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2010) (Learn how and when to remove this message)

• Estadísticas de pedidos en PlanetMath . Consultado el 2 de febrero de 2005.
• Weisstein, Eric W. "Estadística de orden". MathWorld .Recuperado el 2 de febrero de 2005
• Estadísticas de orden dinámico de código fuente C++