Ley de Coulomb

Artículos sobre
Electromagnetismo
Electricity Magnetism Optics History Computational Textbooks Phenomena
Electrostatics Charge density Conductor Coulomb law Electret Electric charge Electric dipole Electric field Electric flux Electric potential Electrostatic discharge Electrostatic induction Gauss law Insulator Permittivity Polarization Potential energy Static electricity Triboelectricity
Magnetostatics Ampère law Biot–Savart law Gauss magnetic law Magnetic dipole Magnetic field Magnetic flux Magnetic scalar potential Magnetic vector potential Magnetization Permeability Right-hand rule
Electrodynamics Bremsstrahlung Cyclotron radiation Displacement current Eddy current Electromagnetic field Electromagnetic induction Electromagnetic pulse Electromagnetic radiation Faraday law Jefimenko equations Larmor formula Lenz law Liénard–Wiechert potential London equations Lorentz force Maxwell equations Maxwell tensor Poynting vector Synchrotron radiation
Electrical network Alternating current Capacitance Current density Direct current Electric current Electric power Electrolysis Electromotive force Impedance Inductance Joule heating Kirchhoff laws Network analysis Ohm law Parallel circuit Resistance Resonant cavities Series circuit Voltage Watt Waveguides
Magnetic circuit AC motor DC motor Electric machine Electric motor Gyrator–capacitor Induction motor Linear motor Magnetomotive force Permeance Reluctance (complex) Reluctance (real) Rotor Stator Transformer
Covariant formulation Electromagnetic tensor Electromagnetism and special relativity Four-current Four-potential Mathematical descriptions Maxwell equations in curved spacetime Relativistic electromagnetism Stress–energy tensor
Scientists Ampère Biot Coulomb Davy Einstein Faraday Fizeau Gauss Heaviside Helmholtz Henry Hertz Hopkinson Jefimenko Joule Kelvin Kirchhoff Larmor Lenz Liénard Lorentz Maxwell Neumann Ohm Ørsted Poisson Poynting Ritchie Savart Singer Steinmetz Tesla Thomson Volta Weber Wiechert
v t e

La ley del cuadrado inverso de Coulomb , o simplemente ley de Coulomb , es una ley experimental ^[1] de la física que calcula la cantidad de fuerza entre dos partículas cargadas eléctricamente en reposo. Esta fuerza eléctrica se denomina convencionalmente fuerza electrostática o fuerza de Coulomb . ^[2] Aunque la ley se conocía antes, fue publicada por primera vez en 1785 por el físico francés Charles-Augustin de Coulomb . La ley de Coulomb fue esencial para el desarrollo de la teoría del electromagnetismo y tal vez incluso su punto de partida, ^[1] ya que permitió discusiones significativas sobre la cantidad de carga eléctrica en una partícula. ^[3]

La ley establece que la magnitud, o valor absoluto, de la fuerza electrostática atractiva o repulsiva entre dos cargas puntuales es directamente proporcional al producto de las magnitudes de sus cargas e inversamente proporcional al cuadrado de la distancia entre ellas. ^[4] Coulomb descubrió que los cuerpos con cargas eléctricas iguales se repelen:

De estas tres pruebas se deduce que la fuerza repulsiva que las dos bolas –[que estaban] electrificadas con el mismo tipo de electricidad– ejercen entre sí sigue la proporción inversa del cuadrado de la distancia. ^[5]

Coulomb también demostró que los cuerpos con carga opuesta se atraen según una ley del cuadrado inverso:$${\displaystyle |F|=k_{\text{e}}{\frac {|q_{1}||q_{2}|}{r^{2}}}}$$

Aquí, k _e es una constante, q ₁ y q ₂ son las cantidades de cada carga y el escalar r es la distancia entre las cargas.

La fuerza se ejerce a lo largo de la línea recta que une las dos cargas. Si las cargas tienen el mismo signo, la fuerza electrostática entre ellas hace que se repelan; si tienen signos diferentes, la fuerza entre ellas hace que se atraigan.

Al ser una ley del cuadrado inverso , la ley es similar a la ley del cuadrado inverso de la gravitación universal de Isaac Newton , pero las fuerzas gravitacionales siempre hacen que las cosas se atraigan, mientras que las fuerzas electrostáticas hacen que las cargas se atraigan o se repelan. Además, las fuerzas gravitacionales son mucho más débiles que las fuerzas electrostáticas. ^[2] La ley de Coulomb se puede utilizar para derivar la ley de Gauss , y viceversa. En el caso de una sola carga puntual en reposo, las dos leyes son equivalentes, expresando la misma ley física de diferentes maneras. ^[6] La ley ha sido probada ampliamente , y las observaciones han confirmado la ley en la escala de 10 ⁻¹⁶ m a 10 ⁸ m. ^[6]

Las culturas antiguas del Mediterráneo sabían que ciertos objetos, como las varillas de ámbar , podían frotarse con pelo de gato para atraer objetos ligeros como plumas y trozos de papel. Tales de Mileto hizo la primera descripción registrada de la electricidad estática alrededor del año 600 a. C., ^[7] cuando notó que la fricción podía hacer que un trozo de ámbar atrajera objetos pequeños. ^{[8] [9]}

En 1600, el científico inglés William Gilbert realizó un estudio cuidadoso de la electricidad y el magnetismo, distinguiendo el efecto imán de la electricidad estática producida por el frotamiento del ámbar. ^[8] Acuñó la palabra neolatina electricus ("de ámbar" o "como el ámbar", de ἤλεκτρον [ elektron ], la palabra griega para "ámbar") para referirse a la propiedad de atraer objetos pequeños después de ser frotados. ^[10] Esta asociación dio lugar a las palabras inglesas "electric" y "electricity", que hicieron su primera aparición impresa en Pseudodoxia Epidemica de Thomas Browne de 1646. ^[11]

Los primeros investigadores del siglo XVIII que sospecharon que la fuerza eléctrica disminuía con la distancia como lo hacía la fuerza de la gravedad (es decir, como el cuadrado inverso de la distancia) incluyeron a Daniel Bernoulli ^[12] y Alessandro Volta , quienes midieron la fuerza entre las placas de un capacitor , y Franz Aepinus, quien supuso la ley del cuadrado inverso en 1758. ^[13]

Basándose en experimentos con esferas cargadas eléctricamente , Joseph Priestley de Inglaterra fue uno de los primeros en proponer que la fuerza eléctrica seguía una ley del cuadrado inverso , similar a la ley de gravitación universal de Newton . Sin embargo, no generalizó ni profundizó en esto. ^[14] En 1767, conjeturó que la fuerza entre cargas variaba como el cuadrado inverso de la distancia. ^{[15] [16]}

En 1769, el físico escocés John Robison anunció que, según sus mediciones, la fuerza de repulsión entre dos esferas con cargas del mismo signo variaba como x ^−2,06 . ^[17]

A principios de la década de 1770, Henry Cavendish de Inglaterra ya había descubierto, pero no publicado, la dependencia de la fuerza entre cuerpos cargados tanto de la distancia como de la carga . ^[18] En sus notas, Cavendish escribió: "Por lo tanto, podemos concluir que la atracción y la repulsión eléctricas deben ser inversamente proporcionales a alguna potencia de la distancia entre la de los 2 + ⁠1/50⁠ º y el del 2 − ⁠1/50⁠ th , y no hay razón para pensar que difiere en absoluto de la relación duplicada inversa".

Finalmente, en 1785, el físico francés Charles-Augustin de Coulomb publicó sus tres primeros informes de electricidad y magnetismo donde enunciaba su ley. Esta publicación fue esencial para el desarrollo de la teoría del electromagnetismo . ^[4] Utilizó una balanza de torsión para estudiar las fuerzas de repulsión y atracción de partículas cargadas , y determinó que la magnitud de la fuerza eléctrica entre dos cargas puntuales es directamente proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia entre ellas.

La balanza de torsión consiste en una barra suspendida en su parte media por una fibra fina. La fibra actúa como un resorte de torsión muy débil . En el experimento de Coulomb, la balanza de torsión era una varilla aislante con una bola recubierta de metal unida a un extremo, suspendida por un hilo de seda . La bola se cargó con una carga conocida de electricidad estática y se acercó a ella una segunda bola cargada de la misma polaridad. Las dos bolas cargadas se repelieron entre sí, torciendo la fibra a través de un cierto ángulo, que podía leerse en una escala en el instrumento . Al saber cuánta fuerza se necesitaba para torcer la fibra a través de un ángulo dado, Coulomb pudo calcular la fuerza entre las bolas y derivar su ley de proporcionalidad del cuadrado inverso.

La ley de Coulomb establece que la fuerza electrostática experimentada por una carga, en la posición , en la proximidad de otra carga, en la posición , en el vacío es igual a ^[19]${\textstyle \mathbf {F} _{1}}$${\displaystyle q_{1}}$${\displaystyle \mathbf {r} _{1}}$${\displaystyle q_{2}}$${\displaystyle \mathbf {r} _{2}}$$${\displaystyle \mathbf {F} _{1}={\frac {q_{1}q_{2}}{4\pi \varepsilon _{0}}}{{\hat {\mathbf {r} }}_{12} \over {|\mathbf {r} _{12}|}^{2}}}$$

donde es el vector de desplazamiento entre las cargas, un vector unitario que apunta desde a , y la constante eléctrica . Aquí, se utiliza para la notación vectorial. La fuerza electrostática experimentada por , según la tercera ley de Newton , es .${\textstyle \mathbf {r_{12}=r_{1}-r_{2}} }$${\textstyle {\hat {\mathbf {r} }}_{12}}$${\textstyle q_{2}}$${\textstyle q_{1}}$${\displaystyle \varepsilon _{0}}$${\textstyle \mathbf {\hat {r}} _{12}}$${\textstyle \mathbf {F} _{2}}$${\displaystyle q_{2}}$${\textstyle \mathbf {F} _{2}=-\mathbf {F} _{1}}$

Si ambas cargas tienen el mismo signo (cargas iguales), entonces el producto es positivo y la dirección de la fuerza sobre está dada por ; las cargas se repelen entre sí. Si las cargas tienen signos opuestos, entonces el producto es negativo y la dirección de la fuerza sobre es ; las cargas se atraen entre sí. ^[20]${\displaystyle q_{1}q_{2}}$${\displaystyle q_{1}}$${\textstyle {\widehat {\mathbf {r} }}_{12}}$${\displaystyle q_{1}q_{2}}$${\displaystyle q_{1}}$${\textstyle -{\hat {\mathbf {r} }}_{12}}$

La ley de superposición permite que la ley de Coulomb se extienda para incluir cualquier número de cargas puntuales. La fuerza que actúa sobre una carga puntual debido a un sistema de cargas puntuales es simplemente la suma vectorial de las fuerzas individuales que actúan solas sobre esa carga puntual debido a cada una de las cargas. El vector de fuerza resultante es paralelo al vector de campo eléctrico en ese punto, con esa carga puntual eliminada.

La fuerza sobre una pequeña carga en la posición , debido a un sistema de cargas discretas en el vacío es ^[19]${\textstyle \mathbf {F} }$${\displaystyle q}$${\displaystyle \mathbf {r} }$${\textstyle n}$

$${\displaystyle \mathbf {F} (\mathbf {r} )={q \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{{\hat {\mathbf {r} }}_{i} \over {|\mathbf {r} _{i}|}^{2}},}$$

donde es la magnitud de la i- ésima carga, es el vector desde su posición hasta y es el vector unitario en la dirección de .${\displaystyle q_{i}}$${\textstyle \mathbf {r} _{i}}$${\displaystyle \mathbf {r} }$${\textstyle {\hat {\mathbf {r} }}_{i}}$${\displaystyle \mathbf {r} _{i}}$

En este caso también se utiliza el principio de superposición lineal . Para una distribución de carga continua, una integral sobre la región que contiene la carga equivale a una suma infinita, tratando cada elemento infinitesimal del espacio como una carga puntual . La distribución de carga suele ser lineal, superficial o volumétrica.${\displaystyle dq}$

Para una distribución de carga lineal (una buena aproximación para la carga en un cable) donde da la carga por unidad de longitud en la posición , y es un elemento infinitesimal de longitud, ^[21]${\displaystyle \lambda (\mathbf {r} ')}$${\displaystyle \mathbf {r} '}$${\displaystyle d\ell '}$$${\displaystyle dq'=\lambda (\mathbf {r'} )\,d\ell '.}$$

Para una distribución de carga superficial (una buena aproximación para la carga en una placa en un capacitor de placas paralelas ) donde da la carga por unidad de área en la posición , y es un elemento infinitesimal de área,${\displaystyle \sigma (\mathbf {r} ')}$${\displaystyle \mathbf {r} '}$${\displaystyle dA'}$$${\displaystyle dq'=\sigma (\mathbf {r'} )\,dA'.}$$

Para una distribución de carga volumétrica (como la carga dentro de un metal a granel), donde da la carga por unidad de volumen en la posición , y es un elemento infinitesimal de volumen, ^[20]${\displaystyle \rho (\mathbf {r} ')}$${\displaystyle \mathbf {r} '}$${\displaystyle dV'}$$${\displaystyle dq'=\rho ({\boldsymbol {r'}})\,dV'.}$$

La fuerza sobre una pequeña carga de prueba en la posición en el vacío está dada por la integral sobre la distribución de carga.${\displaystyle q}$${\displaystyle {\boldsymbol {r}}}$$${\displaystyle \mathbf {F} (\mathbf {r} )={\frac {q}{4\pi \varepsilon _{0}}}\int dq'{\frac {\mathbf {r} -\mathbf {r'} }{|\mathbf {r} -\mathbf {r'} |^{3}}}.}$$

La versión de "carga continua" de la ley de Coulomb nunca se debe aplicar a ubicaciones en las que dicha ubicación se superpondría directamente con la ubicación de una partícula cargada (por ejemplo, un electrón o un protón), lo que no es una ubicación válida para analizar el campo eléctrico o el potencial de manera clásica. La carga siempre es discreta en la realidad, y el supuesto de "carga continua" es solo una aproximación que no se supone que permita su análisis.${\displaystyle |\mathbf {r} -\mathbf {r'} |=0}$${\displaystyle |\mathbf {r} -\mathbf {r'} |=0}$

La constante de proporcionalidad, , en la ley de Coulomb: es una consecuencia de las elecciones históricas de unidades. ^{[19] : 4–2}${\displaystyle {\frac {1}{4\pi \varepsilon _{0}}}}$$${\displaystyle \mathbf {F} _{1}={\frac {q_{1}q_{2}}{4\pi \varepsilon _{0}}}{{\hat {\mathbf {r} }}_{12} \over {|\mathbf {r} _{12}|}^{2}}}$$

La constante es la permitividad eléctrica del vacío . ^[22] Utilizando el valor recomendado por CODATA 2022 para , ^[23] la constante de Coulomb ^[24] es ${\displaystyle \varepsilon _{0}}$${\displaystyle \varepsilon _{0}}$$${\displaystyle k_{\text{e}}={\frac {1}{4\pi \varepsilon _{0}}}=8.987\ 551\ 7862(14)\times 10^{9}\ \mathrm {N{\cdot }m^{2}{\cdot }C^{-2}} .}$$

Hay tres condiciones que deben cumplirse para la validez de la ley del cuadrado inverso de Coulomb: ^[25]

1. Las cargas deben tener una distribución esféricamente simétrica (por ejemplo, cargas puntuales o una esfera metálica cargada).
2. Las cargas no deben superponerse (es decir, deben ser cargas puntuales distintas).
3. Las cargas deben ser estacionarias con respecto a un marco de referencia no acelerado.

La última de ellas se conoce como aproximación electrostática . Cuando se produce un movimiento, se introduce un factor adicional que altera la fuerza producida sobre los dos objetos. Esta parte adicional de la fuerza se denomina fuerza magnética . Para un movimiento lento, la fuerza magnética es mínima y la ley de Coulomb todavía puede considerarse aproximadamente correcta. Sin embargo, una aproximación más precisa en este caso es la fuerza de Weber . Cuando las cargas se mueven más rápidamente entre sí o se producen aceleraciones, deben tenerse en cuenta las ecuaciones de Maxwell y la teoría de la relatividad de Einstein .

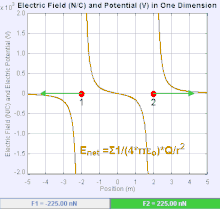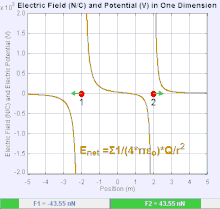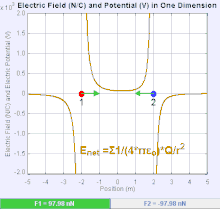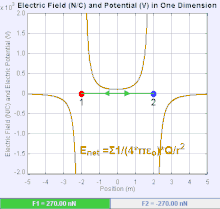
Un campo eléctrico es un campo vectorial que asocia a cada punto del espacio la fuerza de Coulomb experimentada por una carga de prueba unitaria . ^[19] La intensidad y dirección de la fuerza de Coulomb sobre una carga depende del campo eléctrico establecido por otras cargas en las que se encuentra, de modo que . En el caso más simple, se considera que el campo es generado únicamente por una única carga puntual de origen . De manera más general, el campo puede ser generado por una distribución de cargas que contribuyen al conjunto mediante el principio de superposición .${\textstyle \mathbf {F} }$${\textstyle q_{t}}$${\textstyle \mathbf {E} }$${\textstyle \mathbf {F} =q_{t}\mathbf {E} }$

Si el campo es generado por una carga puntual de fuente positiva , la dirección del campo eléctrico apunta a lo largo de líneas dirigidas radialmente hacia afuera desde él, es decir, en la dirección en la que se movería una carga puntual de prueba positiva si se colocara en el campo. Para una carga puntual de fuente negativa, la dirección es radialmente hacia adentro.${\textstyle q}$${\textstyle q_{t}}$

La magnitud del campo eléctrico E se puede derivar de la ley de Coulomb. Al elegir una de las cargas puntuales como fuente y la otra como carga de prueba, se deduce de la ley de Coulomb que la magnitud del campo eléctrico E creado por una única carga puntual Q a una cierta distancia de ella r en el vacío está dada por$${\displaystyle |\mathbf {E} |=k_{\text{e}}{\frac {|q|}{r^{2}}}}$$

Un sistema de n cargas discretas estacionadas en produce un campo eléctrico cuya magnitud y dirección es, por superposición${\displaystyle q_{i}}$${\textstyle \mathbf {r} _{i}=\mathbf {r} -\mathbf {r} _{i}}$$${\displaystyle \mathbf {E} (\mathbf {r} )={1 \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{{\hat {\mathbf {r} }}_{i} \over {|\mathbf {r} _{i}|}^{2}}}$$

La ley de Coulomb se cumple incluso dentro de los átomos , describiendo correctamente la fuerza entre el núcleo atómico cargado positivamente y cada uno de los electrones cargados negativamente . Esta simple ley también explica correctamente las fuerzas que unen a los átomos para formar moléculas y las fuerzas que unen a los átomos y las moléculas para formar sólidos y líquidos. En general, a medida que aumenta la distancia entre los iones , la fuerza de atracción y la energía de enlace se acercan a cero y el enlace iónico es menos favorable. A medida que aumenta la magnitud de las cargas opuestas, aumenta la energía y el enlace iónico es más favorable.

This article duplicates the scope of other articles, specifically Gauss's_law#Relation_to_Coulomb's_law. Please discuss this issue and help introduce a summary style to the article.

En sentido estricto, la ley de Coulomb no puede deducirse únicamente de la ley de Gauss, ya que la ley de Gauss no proporciona ninguna información sobre el rotacional de E (véase la descomposición de Helmholtz y la ley de Faraday ). Sin embargo, la ley de Coulomb puede demostrarse a partir de la ley de Gauss si se supone, además, que el campo eléctrico de una carga puntual es esféricamente simétrico (esta suposición, al igual que la propia ley de Coulomb, es exactamente cierta si la carga está estacionaria y aproximadamente cierta si la carga está en movimiento).

La ley de Coulomb se puede utilizar para obtener información sobre la forma del campo magnético generado por cargas en movimiento, ya que, por la relatividad especial, en ciertos casos se puede demostrar que el campo magnético es una transformación de fuerzas causadas por el campo eléctrico . Cuando no hay aceleración involucrada en la historia de una partícula, se puede suponer la ley de Coulomb en cualquier partícula de prueba en su propio marco inercial, apoyada por argumentos de simetría para resolver la ecuación de Maxwell , que se muestra arriba. La ley de Coulomb se puede ampliar para que las partículas de prueba en movimiento tengan la misma forma. Esta suposición está respaldada por la ley de fuerza de Lorentz que, a diferencia de la ley de Coulomb, no se limita a cargas de prueba estacionarias. Considerando que la carga es invariante del observador, los campos eléctrico y magnético de una carga puntual en movimiento uniforme se pueden derivar por la transformación de Lorentz de las cuatro fuerzas sobre la carga de prueba en el marco de referencia de la carga dado por la ley de Coulomb y atribuyendo los campos magnéticos y eléctricos por sus definiciones dadas por la forma de la fuerza de Lorentz . ^[27] Los campos encontrados para cargas puntuales que se mueven uniformemente se dan por: ^[28] donde es la carga de la fuente puntual, es el vector de posición desde la fuente puntual hasta el punto en el espacio, es el vector de velocidad de la partícula cargada, es la relación entre la velocidad de la partícula cargada dividida por la velocidad de la luz y es el ángulo entre y .$${\displaystyle \mathbf {E} ={\frac {q}{4\pi \epsilon _{0}r^{3}}}{\frac {1-\beta ^{2}}{(1-\beta ^{2}\sin ^{2}\theta )^{3/2}}}\mathbf {r} }$$$${\displaystyle \mathbf {B} ={\frac {q}{4\pi \epsilon _{0}r^{3}}}{\frac {1-\beta ^{2}}{(1-\beta ^{2}\sin ^{2}\theta )^{3/2}}}{\frac {\mathbf {v} \times \mathbf {r} }{c^{2}}}={\frac {\mathbf {v} \times \mathbf {E} }{c^{2}}}}$$${\displaystyle q}$${\displaystyle \mathbf {r} }$${\displaystyle \mathbf {v} }$${\displaystyle \beta }$${\displaystyle \theta }$${\displaystyle \mathbf {r} }$${\displaystyle \mathbf {v} }$

Esta forma de soluciones no necesita obedecer la tercera ley de Newton como es el caso en el marco de la relatividad especial (sin violar la conservación del momento de la energía relativista). ^[29] Nótese que la expresión para el campo eléctrico se reduce a la ley de Coulomb para velocidades no relativistas de la carga puntual y que el campo magnético en el límite no relativista (aproximando ) se puede aplicar a corrientes eléctricas para obtener la ley de Biot-Savart . Estas soluciones, cuando se expresan en tiempo retardado también corresponden a la solución general de las ecuaciones de Maxwell dadas por soluciones del potencial de Liénard-Wiechert , debido a la validez de la ley de Coulomb dentro de su rango específico de aplicación. Nótese también que la simetría esférica para la ley de Gauss en cargas estacionarias no es válida para cargas en movimiento debido a la ruptura de la simetría por la especificación de la dirección de la velocidad en el problema. La concordancia con las ecuaciones de Maxwell también se puede verificar manualmente para las dos ecuaciones anteriores. ^[30]${\displaystyle \beta \ll 1}$

This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (October 2020) (Learn how and when to remove this message)

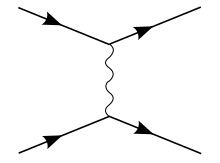
El potencial de Coulomb admite estados continuos (con E > 0), que describen la dispersión electrón-protón , así como estados ligados discretos, que representan al átomo de hidrógeno. ^[31] También se puede derivar dentro del límite no relativista entre dos partículas cargadas, de la siguiente manera:

Según la aproximación de Born , en la mecánica cuántica no relativista, la amplitud de dispersión es: Esto se debe comparar con: donde observamos la entrada de la matriz S (conectada) para dos electrones que se dispersan entre sí, tratando a uno con momento "fijo" como la fuente del potencial y al otro dispersándose desde ese potencial.${\textstyle {\mathcal {A}}(|\mathbf {p} \rangle \to |\mathbf {p} '\rangle )}$$${\displaystyle {\mathcal {A}}(|\mathbf {p} \rangle \to |\mathbf {p} '\rangle )-1=2\pi \delta (E_{p}-E_{p'})(-i)\int d^{3}\mathbf {r} \,V(\mathbf {r} )e^{-i(\mathbf {p} -\mathbf {p} ')\mathbf {r} }}$$$${\displaystyle \int {\frac {d^{3}k}{(2\pi )^{3}}}e^{ikr_{0}}\langle p',k|S|p,k\rangle }$$

Usando las reglas de Feynman para calcular el elemento de la matriz S, obtenemos en el límite no relativista con${\displaystyle m_{0}\gg |\mathbf {p} |}$$${\displaystyle \langle p',k|S|p,k\rangle |_{conn}=-i{\frac {e^{2}}{|\mathbf {p} -\mathbf {p} '|^{2}-i\varepsilon }}(2m)^{2}\delta (E_{p,k}-E_{p',k})(2\pi )^{4}\delta (\mathbf {p} -\mathbf {p} ')}$$

En comparación con la dispersión QM, tenemos que descartar ya que surgen debido a las diferentes normalizaciones del estado propio del momento en QFT en comparación con QM y obtener: donde la transformada de Fourier en ambos lados, resolviendo la integral y tomando al final dará como resultado el potencial de Coulomb. ^[32]${\displaystyle (2m)^{2}}$$${\displaystyle \int V(\mathbf {r} )e^{-i(\mathbf {p} -\mathbf {p} ')\mathbf {r} }d^{3}\mathbf {r} ={\frac {e^{2}}{|\mathbf {p} -\mathbf {p} '|^{2}-i\varepsilon }}}$$${\displaystyle \varepsilon \to 0}$$${\displaystyle V(r)={\frac {e^{2}}{4\pi r}}}$$

Sin embargo, se piensa que los resultados equivalentes de las derivaciones clásicas de Born para el problema de Coulomb son estrictamente accidentales. ^{[33] [34]}

El potencial de Coulomb y su derivación pueden verse como un caso especial del potencial de Yukawa , que es el caso en el que el bosón intercambiado (el fotón) no tiene masa en reposo. ^[31]

This section may contain an excessive amount of intricate detail that may interest only a particular audience. Please help by spinning off or relocating any relevant information, and removing excessive detail that may be against Wikipedia's inclusion policy. (October 2020) (Learn how and when to remove this message)

Es posible comprobar la ley de Coulomb con un experimento sencillo. Consideremos dos esferas pequeñas de masa y carga del mismo signo , colgadas de dos cuerdas de masa despreciable y longitud . Las fuerzas que actúan sobre cada esfera son tres: el peso , la tensión de la cuerda y la fuerza eléctrica . En el estado de equilibrio: ${\displaystyle m}$${\displaystyle q}$${\displaystyle l}$${\displaystyle mg}$${\displaystyle \mathbf {T} }$${\displaystyle \mathbf {F} }$

$${\displaystyle \mathbf {T} \sin \theta _{1}=\mathbf {F} _{1}}$$

( 1 )

y

$${\displaystyle \mathbf {T} \cos \theta _{1}=mg}$$

( 2 )

Dividiendo ( 1 ) por ( 2 ):

$${\displaystyle {\frac {\sin \theta _{1}}{\cos \theta _{1}}}={\frac {F_{1}}{mg}}\Rightarrow F_{1}=mg\tan \theta _{1}}$$

( 3 )

Sea la distancia entre las esferas cargadas; la fuerza de repulsión entre ellas , suponiendo que la ley de Coulomb es correcta, es igual a${\displaystyle \mathbf {L} _{1}}$${\displaystyle \mathbf {F} _{1}}$

$${\displaystyle F_{1}={\frac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}}$$

( Ley de Coulomb )

entonces:

$${\displaystyle {\frac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}=mg\tan \theta _{1}}$$

( 4 )

Si ahora descargamos una de las esferas, y la ponemos en contacto con la esfera cargada, cada una de ellas adquiere una carga . En el estado de equilibrio, la distancia entre las cargas será y la fuerza de repulsión entre ellas será:${\textstyle {\frac {q}{2}}}$${\textstyle \mathbf {L} _{2}<\mathbf {L} _{1}}$

$${\displaystyle F_{2}={\frac {{({\frac {q}{2}})}^{2}}{4\pi \varepsilon _{0}L_{2}^{2}}}={\frac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}}$$

( 5 )

Sabemos que y: Dividiendo ( 4 ) por ( 5 ), obtenemos: ${\displaystyle \mathbf {F} _{2}=mg\tan \theta _{2}}$$${\displaystyle {\frac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}=mg\tan \theta _{2}}$$

$${\displaystyle {\frac {\left({\cfrac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}\right)}{\left({\cfrac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}\right)}}={\frac {mg\tan \theta _{1}}{mg\tan \theta _{2}}}\Rightarrow 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}={\frac {\tan \theta _{1}}{\tan \theta _{2}}}}$$

( 6 )

Medir los ángulos y y la distancia entre las cargas y es suficiente para verificar que la igualdad es cierta teniendo en cuenta el error experimental. En la práctica, los ángulos pueden ser difíciles de medir, por lo que si la longitud de las cuerdas es suficientemente grande, los ángulos serán lo suficientemente pequeños como para hacer la siguiente aproximación:${\displaystyle \theta _{1}}$${\displaystyle \theta _{2}}$${\displaystyle \mathbf {L} _{1}}$${\displaystyle \mathbf {L} _{2}}$

$${\displaystyle \tan \theta \approx \sin \theta ={\frac {\frac {L}{2}}{\ell }}={\frac {L}{2\ell }}\Rightarrow {\frac {\tan \theta _{1}}{\tan \theta _{2}}}\approx {\frac {\frac {L_{1}}{2\ell }}{\frac {L_{2}}{2\ell }}}}$$

( 7 )

Utilizando esta aproximación, la relación ( 6 ) se convierte en la expresión mucho más simple:

$${\displaystyle {\frac {\frac {L_{1}}{2\ell }}{\frac {L_{2}}{2\ell }}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow {\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}}$$

( 8 )

De esta manera, la verificación se limita a medir la distancia entre las cargas y comprobar que la división se aproxima al valor teórico.

Spavieri, G., Gillies, GT y Rodriguez, M. (2004). Implicaciones físicas de la Ley de Coulomb. Metrologia, 41(5), S159–S170. doi:10.1088/0026-1394/41/5/s06 

• Coulomb, Charles Augustin (1788) [1785]. "Premier mémoire sur l'électricité et le magnétisme". Historia de la Academia Real de Ciencias . Imprimerie Royale. págs. 569–577.
• Coulomb, Charles Augustin (1788) [1785]. "Segunda memoria sobre la electricidad y el magnetismo". Historia de la Academia Real de Ciencias . Imprimerie Royale. págs. 578–611.
• Coulomb, Charles Augustin (1788) [1785]. "Troisième mémoire sur l'électricité et le magnétisme". Historia de la Academia Real de Ciencias . Imprimerie Royale. págs. 612–638.
• Griffiths, David J. (1999). Introducción a la electrodinámica (3.ª ed.). Prentice Hall. ISBN 978-0-13-805326-0.
• Tamm, Igor E. (1979) [1976]. Fundamentos de la teoría de la electricidad (9.ª ed.). Moscú: Mir. pp. 23–27.
• Tipler, Paul A.; Mosca, Gene (2008). Física para científicos e ingenieros (6.ª ed.). Nueva York: WH Freeman and Company. ISBN 978-0-7167-8964-2. Número de serie LCCN  2007010418.
• Young, Hugh D.; Freedman, Roger A. (2010). Física universitaria de Sears y Zemansky: con física moderna (13.ª ed.). Addison-Wesley (Pearson). ISBN 978-0-321-69686-1.

Wikimedia Commons alberga una categoría multimedia sobre Ley de Coulomb .

• Ley de Coulomb en el proyecto PHYSNET
• La electricidad y el átomo Archivado el 21 de febrero de 2009 en Wayback Machine —un capítulo de un libro de texto en línea
• Un juego de laberinto para enseñar la ley de Coulomb: un juego creado por el software Molecular Workbench
• Cargas eléctricas, polarización, fuerza eléctrica, ley de Coulomb Walter Lewin, 8.02 Electricidad y magnetismo, primavera de 2002: lección 1 (vídeo). MIT OpenCourseWare. Licencia: Creative Commons Attribution-Noncommercial-Share Alike.