Ecuaciones de Euler (dinámica de fluidos)

En dinámica de fluidos , las ecuaciones de Euler son un conjunto de ecuaciones diferenciales parciales que rigen el flujo adiabático y no viscoso . Reciben su nombre de Leonhard Euler . En particular, corresponden a las ecuaciones de Navier-Stokes con viscosidad cero y conductividad térmica cero . [1]
Las ecuaciones de Euler se pueden aplicar a flujos incompresibles y compresibles . Las ecuaciones de Euler incompresibles consisten en ecuaciones de Cauchy para la conservación de la masa y el equilibrio del momento, junto con la condición de incompresibilidad de que la velocidad del flujo es un campo solenoidal . Las ecuaciones de Euler compresibles consisten en ecuaciones para la conservación de la masa, el equilibrio del momento y el equilibrio de la energía, junto con una ecuación constitutiva adecuada para la densidad de energía específica del fluido. Históricamente, Euler solo derivó las ecuaciones de conservación de la masa y el equilibrio del momento. Sin embargo, la literatura sobre dinámica de fluidos a menudo se refiere al conjunto completo de ecuaciones de Euler compresibles, incluida la ecuación de la energía, como "las ecuaciones de Euler compresibles". [2]
Las características matemáticas de las ecuaciones de Euler incompresibles y compresibles son bastante diferentes. Para una densidad de fluido constante, las ecuaciones incompresibles pueden escribirse como una ecuación de advección cuasilineal para la velocidad del fluido junto con una ecuación de Poisson elíptica para la presión. Por otro lado, las ecuaciones de Euler compresibles forman un sistema hiperbólico cuasilineal de ecuaciones de conservación .
Las ecuaciones de Euler pueden formularse en una "forma convectiva" (también llamada " forma lagrangiana ") o en una "forma de conservación" (también llamada " forma euleriana "). La forma convectiva enfatiza los cambios de estado en un marco de referencia que se mueve con el fluido. La forma de conservación enfatiza la interpretación matemática de las ecuaciones como ecuaciones de conservación para un volumen de control fijo en el espacio (lo cual es útil desde un punto de vista numérico).
Historia
Las ecuaciones de Euler aparecieron por primera vez en forma publicada en el artículo de Euler "Principes généraux du mouvement des fluides", publicado en Mémoires de l'Académie des Sciences de Berlin en 1757 [3] (aunque Euler ya había presentado su trabajo en la Academia de Berlín en 1752). [4] Los trabajos anteriores incluían contribuciones de la familia Bernoulli , así como de Jean le Rond d'Alembert . [5]
Las ecuaciones de Euler estuvieron entre las primeras ecuaciones diferenciales parciales que se escribieron, después de la ecuación de onda . En el trabajo original de Euler, el sistema de ecuaciones consistía en las ecuaciones de momento y continuidad, y por lo tanto estaba subdeterminado excepto en el caso de un flujo incompresible. Pierre-Simon Laplace propuso una ecuación adicional, llamada condición adiabática , en 1816.
Durante la segunda mitad del siglo XIX, se descubrió que la ecuación relacionada con el balance de energía debe mantenerse en todo momento para flujos compresibles, y la condición adiabática es una consecuencia de las leyes fundamentales en el caso de soluciones suaves. Con el descubrimiento de la teoría especial de la relatividad , los conceptos de densidad de energía, densidad de momento y tensión se unificaron en el concepto de tensor de tensión-energía , y la energía y el momento se unificaron asimismo en un solo concepto, el vector de energía-momento . [4]
Ecuaciones de Euler incompresibles con densidad constante y uniforme
En forma convectiva (es decir, la forma con el operador convectivo hecho explícito en la ecuación del momento ), las ecuaciones de Euler incompresibles en caso de densidad constante en el tiempo y uniforme en el espacio son: [6]
( forma convectiva o lagrangiana )
dónde:
- es el vector de velocidad de flujo , con componentes en un espacio N -dimensional ,
- , para una función (o campo) genérico denota su derivada material en el tiempo con respecto al campo advectivo y
- es el gradiente del trabajo termodinámico específico (con el sentido de por unidad de masa ) , el término de fuente interna , y
- es la divergencia de la velocidad del flujo .
- representa aceleraciones corporales (por unidad de masa) que actúan sobre el continuo, por ejemplo , la gravedad , las aceleraciones inerciales, la aceleración del campo eléctrico , etc.
La primera ecuación es la ecuación de Euler del momento con densidad uniforme (para esta ecuación también podría no ser constante en el tiempo). Al desarrollar la derivada material , las ecuaciones se convierten en:
De hecho, para un flujo con densidad uniforme se cumple la siguiente identidad: donde es la presión mecánica . La segunda ecuación es la restricción incompresible , que establece que la velocidad del flujo es un campo solenoidal (el orden de las ecuaciones no es causal, pero subraya el hecho de que la restricción incompresible no es una forma degenerada de la ecuación de continuidad , sino más bien de la ecuación de energía, como se aclarará a continuación). Cabe destacar que la ecuación de continuidad también sería necesaria en este caso incompresible como una tercera ecuación adicional en caso de que la densidad varíe en el tiempo o varíe en el espacio. Por ejemplo, con una densidad no uniforme en el espacio pero constante en el tiempo, la ecuación de continuidad que se añadiría al conjunto anterior correspondería a:
Así, el caso de densidad constante y uniforme es el único que no requiere la ecuación de continuidad como ecuación adicional, independientemente de la presencia o ausencia de la restricción de incompresibilidad. De hecho, el caso de ecuaciones de Euler incompresibles con densidad constante y uniforme que se analiza aquí es un modelo de juguete que presenta solo dos ecuaciones simplificadas, por lo que es ideal para fines didácticos, aunque tenga una relevancia física limitada.
Las ecuaciones anteriores representan respectivamente la conservación de la masa (1 ecuación escalar) y del momento (1 ecuación vectorial que contiene componentes escalares, donde es la dimensión física del espacio de interés). La velocidad y la presión del flujo son las denominadas variables físicas . [1]
En un sistema de coordenadas dado por los vectores de velocidad y fuerza externa y tienen componentes y , respectivamente. Entonces las ecuaciones pueden expresarse en notación de subíndice como:
donde los subíndices y etiquetan los componentes del espacio N -dimensional, y es el delta de Kroenecker . El uso de la notación de Einstein (donde la suma está implícita por índices repetidos en lugar de la notación sigma ) también es frecuente.
Propiedades
Aunque Euler presentó por primera vez estas ecuaciones en 1755, muchas preguntas o conceptos fundamentales sobre ellas siguen sin respuesta.
En tres dimensiones espaciales, en ciertos escenarios simplificados, las ecuaciones de Euler producen singularidades. [7]
Las soluciones suaves de las ecuaciones libres (en el sentido de sin término fuente: g=0) satisfacen la conservación de la energía cinética específica:
En el caso unidimensional sin el término fuente (tanto gradiente de presión como fuerza externa), la ecuación del momento se convierte en la ecuación de Burgers no viscosa :
Esta ecuación modelo proporciona muchas ideas sobre las ecuaciones de Euler.
No dimensionalización
Para que las ecuaciones sean adimensionales, es necesario definir una longitud característica y una velocidad característica . Estas deben elegirse de modo que las variables adimensionales sean todas de orden uno. De este modo, se obtienen las siguientes variables adimensionales: y del vector unitario de campo :
La sustitución de estas relaciones inversas en las ecuaciones de Euler, que definen el número de Froude , da como resultado (omitiendo el * en apix):
( forma adimensional )
Las ecuaciones de Euler en el límite de Froude (sin campo externo) se denominan ecuaciones libres y son conservativas. El límite de números de Froude altos (campo externo bajo) es, por lo tanto, notable y se puede estudiar con la teoría de perturbaciones .
Formulario de conservación
La forma conservada enfatiza las propiedades matemáticas de las ecuaciones de Euler, y especialmente la forma contraída es a menudo la más conveniente para las simulaciones computacionales de dinámica de fluidos . Desde el punto de vista computacional, existen algunas ventajas en el uso de las variables conservadas. Esto da lugar a una gran clase de métodos numéricos llamados métodos conservadores. [1]
Las ecuaciones de Euler libres son conservativas , en el sentido de que son equivalentes a una ecuación de conservación: o simplemente en notación de Einstein: donde la cantidad de conservación en este caso es un vector, y es una matriz de flujo . Esto se puede demostrar de forma sencilla.
En primer lugar, se cumplen las siguientes identidades: donde denota el producto externo . Las mismas identidades expresadas en notación de Einstein son: donde I es la matriz identidad con dimensión N y δ ij su elemento general, el delta de Kroenecker.
Gracias a estas identidades vectoriales, las ecuaciones de Euler incompresibles con densidad constante y uniforme y sin campo externo se pueden poner en la llamada forma diferencial de conservación (o euleriana), con notación vectorial: o con notación de Einstein:
Entonces, las ecuaciones de Euler incompresibles con densidad uniforme tienen variables de conservación:
Nótese que en el segundo componente u es en sí mismo un vector, con longitud N, por lo que y tiene longitud N+1 y F tiene tamaño N(N+1). En 3D, por ejemplo, y tiene longitud 4, I tiene tamaño 3×3 y F tiene tamaño 4×3, por lo que las formas explícitas son:
Por último, las ecuaciones de Euler pueden reformularse en la ecuación particular:
( forma de conservación o euleriana )
Dimensiones espaciales
Para ciertos problemas, especialmente cuando se utilizan para analizar el flujo compresible en un conducto o en caso de que el flujo sea cilíndrica o esféricamente simétrico, las ecuaciones de Euler unidimensionales son una primera aproximación útil. Generalmente, las ecuaciones de Euler se resuelven mediante el método de características de Riemann . Esto implica encontrar curvas en el plano de variables independientes (es decir, y ) a lo largo de las cuales las ecuaciones diferenciales parciales (EDP) degeneran en ecuaciones diferenciales ordinarias (EDO). Las soluciones numéricas de las ecuaciones de Euler dependen en gran medida del método de características.
Ecuaciones de Euler incompresibles
En forma convectiva las ecuaciones de Euler incompresibles en caso de densidad variable en el espacio son: [6]
( forma convectiva o lagrangiana )
donde las variables adicionales son:
- es la densidad de masa del fluido ,
- es la presión , .
La primera ecuación, que es la nueva, es la ecuación de continuidad incompresible . En realidad la ecuación general de continuidad sería:
pero aquí el último término es idénticamente cero para la restricción de incompresibilidad.
Formulario de conservación
Las ecuaciones de Euler incompresibles en el límite de Froude son equivalentes a una única ecuación de conservación con cantidad conservada y flujo asociado respectivamente:
Aquí tiene longitud y tiene tamaño . [a] En general (no sólo en el límite de Froude) las ecuaciones de Euler se pueden expresar como:
Variables de conservación
Las variables para las ecuaciones en forma de conservación aún no están optimizadas. De hecho, podríamos definir: donde es la densidad de momento , una variable de conservación.
( forma de conservación o euleriana )
donde es la densidad de fuerza , una variable de conservación.
Ecuaciones de Euler
En forma convectiva diferencial, las ecuaciones de Euler compresibles (y más generales) se pueden escribir brevemente con la notación de derivada material :
( forma convectiva )
donde las variables adicionales aquí son:
- es la energía interna específica (energía interna por unidad de masa).
Las ecuaciones anteriores representan, por tanto, la conservación de la masa , el momento y la energía : la ecuación de la energía expresada en la variable energía interna permite entender la relación con el caso incompresible, pero no está en la forma más simple. La densidad de masa, la velocidad del flujo y la presión son las llamadas variables convectivas (o variables físicas, o variables lagrangianas), mientras que la densidad de masa, la densidad del momento y la densidad de energía total son las llamadas variables conservadas (también llamadas variables eulerianas o matemáticas). [1]
Si se desarrolla la derivada material las ecuaciones anteriores son:
Restricción incompresible (revisitada)
Volviendo al caso incompresible, ahora resulta evidente que la restricción incompresible típica de los casos anteriores es en realidad una forma particular válida para flujos incompresibles de la ecuación de energía y no de la ecuación de masa. En particular, la restricción incompresible corresponde a la siguiente ecuación de energía muy simple:
Así, para un fluido incompresible no viscoso, la energía interna específica es constante a lo largo de las líneas de flujo , también en un flujo dependiente del tiempo. La presión en un flujo incompresible actúa como un multiplicador de Lagrange , siendo el multiplicador de la restricción incompresible en la ecuación de energía, y en consecuencia en flujos incompresibles no tiene significado termodinámico. De hecho, la termodinámica es típica de los flujos compresibles y degenera en flujos incompresibles. [8]
Basándonos en la ecuación de conservación de masa, se puede poner esta ecuación en forma de conservación: lo que significa que para un flujo no viscoso, incompresible y no conductor, se cumple una ecuación de continuidad para la energía interna.
Conservación de la entalpía
Ya que por definición la entalpía específica es:
La derivada material de la energía interna específica se puede expresar como:
Luego, sustituyendo la ecuación del momento en esta expresión, se obtiene:
Y sustituyendo este último en la ecuación de energía, se obtiene que la expresión de entalpía para la ecuación de energía de Euler: En un marco de referencia que se mueve con un flujo no viscoso y no conductor, la variación de la entalpía corresponde directamente a una variación de la presión.
Termodinámica de fluidos ideales
En termodinámica, las variables independientes son el volumen específico y la entropía específica , mientras que la energía específica es una función del estado de estas dos variables.
Teniendo en cuenta la primera ecuación, la variable debe cambiarse de densidad a volumen específico. Por definición:
Por tanto se cumplen las siguientes identidades:
Luego, sustituyendo estas expresiones en la ecuación de conservación de masa:
Y por multiplicación:
Esta ecuación es la única que pertenece a las ecuaciones generales del continuo, por lo que sólo esta ecuación tiene la misma forma, por ejemplo, también en las ecuaciones de Navier-Stokes.
Por otra parte, la presión en termodinámica es la opuesta de la derivada parcial de la energía interna específica con respecto al volumen específico: dado que la energía interna en termodinámica es una función de las dos variables mencionadas anteriormente, el gradiente de presión contenido en la ecuación del momento debe explicitarse como:
Es conveniente por brevedad cambiar la notación para las derivadas de segundo orden:
Finalmente, la ecuación de energía: se puede simplificar aún más en forma convectiva cambiando la variable de energía específica a entropía específica: de hecho, la primera ley de la termodinámica en forma local se puede escribir: sustituyendo la derivada material de la energía interna, la ecuación de energía se convierte en: ahora el término entre paréntesis es idénticamente cero de acuerdo con la conservación de la masa, entonces la ecuación de energía de Euler se convierte simplemente en:
Para un fluido termodinámico, las ecuaciones de Euler compresibles se escriben mejor de la siguiente manera:
( forma convectiva, para un sistema termodinámico )
dónde:
- es el volumen específico
- es el vector de velocidad de flujo
- es la entropía específica
En el caso general y no solo en el caso incompresible, la ecuación de energía significa que para un fluido termodinámico no viscoso la entropía específica es constante a lo largo de las líneas de flujo , también en un flujo dependiente del tiempo. Basándose en la ecuación de conservación de la masa, se puede poner esta ecuación en la forma de conservación: [9] lo que significa que para un flujo no viscoso no conductor se cumple una ecuación de continuidad para la entropía.
Por otra parte, las dos derivadas parciales de segundo orden de la energía interna específica en la ecuación del momento requieren la especificación de la ecuación de estado fundamental del material considerado, es decir de la energía interna específica en función de las dos variables volumen específico y entropía específica:
La ecuación de estado fundamental contiene toda la información termodinámica del sistema (Callen, 1985), [10] exactamente como el par de una ecuación de estado térmica junto con una ecuación de estado calórica .
Formulario de conservación
Las ecuaciones de Euler en el límite de Froude son equivalentes a una única ecuación de conservación con cantidad conservada y flujo asociado respectivamente:
dónde:
- es la densidad de momento , una variable de conservación.
- es la densidad total de energía (energía total por unidad de volumen).
Aquí tiene longitud N + 2 y tamaño N(N + 2). [b] En general (no solo en el límite de Froude) las ecuaciones de Euler se pueden expresar como:
( conservación original o forma euleriana )
donde es la densidad de fuerza , una variable de conservación.
Observamos que también la ecuación de Euler, incluso cuando es conservativa (sin campo externo, límite de Froude), no tiene invariantes de Riemann en general. [11] Se requieren algunas suposiciones adicionales .
Sin embargo, ya mencionamos que para un fluido termodinámico la ecuación para la densidad de energía total es equivalente a la ecuación de conservación:
Entonces las ecuaciones de conservación en el caso de un fluido termodinámico se expresan de manera más simple como:
( forma de conservación, para fluidos termodinámicos )
donde es la densidad de entropía, una variable de conservación termodinámica.
Otra forma posible para la ecuación de energía, particularmente útil para isobáricas , es: donde es la densidad de entalpía total .
Forma cuasilineal y ecuaciones características
La expansión de los flujos puede ser una parte importante de la construcción de solucionadores numéricos , por ejemplo, explotando soluciones ( aproximadas ) al problema de Riemann . En regiones donde el vector de estado y varía suavemente, las ecuaciones en forma conservativa se pueden poner en forma cuasilineal: donde se denominan jacobianos de flujo definidos como las matrices :
Obviamente, este jacobiano no existe en regiones de discontinuidad (por ejemplo, discontinuidades de contacto, ondas de choque en flujos no viscosos no conductores). Si los jacobianos de flujo no son funciones del vector de estado , las ecuaciones revelan que son lineales .
Ecuaciones características
Las ecuaciones de Euler compresibles se pueden desacoplar en un conjunto de ecuaciones de onda N+2 que describen el sonido en el continuo euleriano si se expresan en variables características en lugar de variables conservadas.
De hecho, el tensor A es siempre diagonalizable . Si los valores propios (el caso de las ecuaciones de Euler) son todos reales, el sistema se define como hiperbólico , y físicamente los valores propios representan las velocidades de propagación de la información. [12] Si se distinguen todos, el sistema se define como estrictamente hiperbólico (se demostrará que es el caso de las ecuaciones de Euler unidimensionales). Además, la diagonalización de la ecuación de Euler compresible es más fácil cuando la ecuación de energía se expresa en la variable entropía (es decir, con ecuaciones para fluidos termodinámicos) que en otras variables de energía. Esto quedará claro al considerar el caso 1D.
Si es el vector propio derecho de la matriz correspondiente al valor propio , construyendo la matriz de proyección :
Finalmente podemos encontrar las variables características como:
Como A es constante, al multiplicar la ecuación 1-D original en forma jacobiana de flujo por P −1 se obtienen las ecuaciones características: [13]
Las ecuaciones originales se han desacoplado en N+2 ecuaciones características, cada una de las cuales describe una onda simple, en la que los valores propios son las velocidades de onda. Las variables w i se denominan variables características y son un subconjunto de las variables conservadoras. La solución del problema del valor inicial en términos de variables características es finalmente muy sencilla. En una dimensión espacial es:
Luego, la solución en términos de las variables conservadoras originales se obtiene transformando nuevamente: este cálculo se puede explicitar como la combinación lineal de los vectores propios:
Ahora resulta evidente que las variables características actúan como pesos en la combinación lineal de los vectores propios jacobianos. La solución puede verse como una superposición de ondas, cada una de las cuales se transporta independientemente sin cambio de forma. Cada onda i -ésima tiene forma w i p i y velocidad de propagación λ i . A continuación mostramos un ejemplo muy simple de este procedimiento de solución.
Ondas en un fluido termodinámico unidimensional no viscoso y no conductor
Si se consideran las ecuaciones de Euler para un fluido termodinámico con los dos supuestos adicionales de una dimensión espacial y libre (sin campo externo: g = 0):
Si se define el vector de variables: recordando que es el volumen específico, la velocidad del flujo, la entropía específica, la matriz jacobiana correspondiente es:
Primero hay que encontrar los valores propios de esta matriz resolviendo la ecuación característica :
Esto es explícitamente:
Este determinante es muy simple: el cálculo más rápido comienza en la última fila, ya que tiene el mayor número de elementos cero.
Ahora calculando el determinante 2×2: definiendo el parámetro: o equivalentemente en variables mecánicas, como:
Este parámetro es siempre real según la segunda ley de la termodinámica . De hecho, la segunda ley de la termodinámica puede expresarse mediante varios postulados. El más elemental de ellos en términos matemáticos es el enunciado de la convexidad de la ecuación de estado fundamental, es decir, la matriz hessiana de la energía específica expresada en función del volumen específico y de la entropía específica: se define positiva. Este enunciado corresponde a las dos condiciones:
La primera condición es la que garantiza que el parámetro a se defina como real.
La ecuación característica finalmente resulta:
Esto tiene tres soluciones reales:
Entonces la matriz tiene tres valores propios reales, todos distinguidos: las ecuaciones de Euler 1D son un sistema estrictamente hiperbólico.
En este punto se deben determinar los tres vectores propios: cada uno se obtiene sustituyendo un valor propio en la ecuación de valores propios y luego resolviéndola. Sustituyendo el primer valor propio λ 1 se obtiene:
Basándonos en la tercera ecuación que simplemente tiene solución s 1 = 0, el sistema se reduce a:
Las dos ecuaciones son redundantes como es habitual, por lo que el vector propio se define con una constante multiplicativa. Elegimos como vector propio derecho:
Los otros dos vectores propios se pueden encontrar con un procedimiento análogo como:
Luego la matriz de proyección se puede construir:
Finalmente se hace evidente que el parámetro real a definido anteriormente es la velocidad de propagación de la información característica del sistema hiperbólico formado por ecuaciones de Euler, es decir, es la velocidad de onda . Queda por demostrar que la velocidad del sonido corresponde al caso particular de una transformación isentrópica :
Compresibilidad y velocidad del sonido
La velocidad del sonido se define como la velocidad de onda de una transformación isentrópica: por la definición de compresibilidad isoentrópica: la velocidad del sonido resulta siempre la raíz cuadrada de la relación entre la compresibilidad isentrópica y la densidad:
Gas ideal
La velocidad del sonido en un gas ideal depende únicamente de su temperatura:
En un gas ideal la transformación isoentrópica se describe mediante la ley de Poisson: donde γ es la relación de capacidad térmica , una constante para el material. Explícitando las diferenciales:
y dividiendo por ρ − γ d ρ :
Luego, por sustitución en las definiciones generales de un gas ideal, la compresibilidad isentrópica es simplemente proporcional a la presión:
y los resultados de la velocidad del sonido ( ley de Newton-Laplace ):
En particular, para un gas ideal se cumple la ley de los gases ideales , que en forma matemática es simplemente:
donde n es la densidad numérica y T es la temperatura absoluta , siempre que se mida en unidades energéticas (es decir, en julios ) mediante la multiplicación por la constante de Boltzmann . Como la densidad de masa es proporcional a la densidad numérica a través de la masa molecular media m del material:
La ley de los gases ideales se puede reformular en la fórmula:
Sustituyendo esta relación en la ley de Newton-Laplace, se consigue finalmente la expresión de la velocidad del sonido en un gas ideal en función de la temperatura.
Dado que la entalpía específica en un gas ideal es proporcional a su temperatura:
La velocidad del sonido en un gas ideal también puede hacerse dependiente únicamente de su entalpía específica:
Teorema de Bernoulli para flujo no viscoso estacionario
El teorema de Bernoulli es una consecuencia directa de las ecuaciones de Euler.
Caso incompresible y forma de Lamb
La identidad del cálculo vectorial del producto vectorial de un rizo se cumple:
donde se utiliza la notación de subíndice de Feynman , lo que significa que el gradiente subíndice opera solo en el factor .
Lamb, en su famoso libro clásico Hidrodinámica (1895), todavía impreso, utilizó esta identidad para cambiar el término convectivo de la velocidad del flujo en forma rotacional: [14]
La ecuación del momento de Euler en forma de Lamb se convierte en:
Ahora, basándonos en la otra identidad:
La ecuación del momento de Euler asume una forma que es óptima para demostrar el teorema de Bernoulli para flujos estables:
De hecho, en el caso de un campo conservativo externo , al definir su potencial φ:
En el caso de un flujo constante, la derivada temporal de la velocidad del flujo desaparece, por lo que la ecuación del momento se convierte en:
Y al proyectar la ecuación del momento sobre la dirección del flujo, es decir a lo largo de una línea de corriente , el producto vectorial desaparece porque su resultado es siempre perpendicular a la velocidad:
En el caso incompresible estacionario la ecuación de masa es simplemente:
Es decir, la conservación de la masa para un flujo incompresible estable establece que la densidad a lo largo de una línea de corriente es constante . Entonces, la ecuación de momento de Euler en el caso incompresible estable se convierte en:
Ahora resulta evidente la conveniencia de definir la altura total para un flujo de líquido no viscoso:
que puede escribirse simplemente como:
Es decir, el equilibrio de momento para un flujo constante no viscoso e incompresible en un campo conservativo externo establece que la altura total a lo largo de una línea de corriente es constante .
Estuche comprimible
En el caso más general estable (compresible), la ecuación de masa en forma de conservación es:
Por lo tanto, la expresión anterior es más bien
El lado derecho aparece en la ecuación de energía en forma convectiva, que en estado estacionario se lee:
La ecuación energética por tanto queda así:
De modo que la energía interna específica ahora se concentra en la cabeza.
Como el potencial de campo externo suele ser pequeño en comparación con los otros términos, es conveniente agrupar estos últimos en la entalpía total :
y el invariante de Bernoulli para un flujo de gas no viscoso es:
que puede escribirse como:
Es decir, el balance de energía para un flujo no viscoso constante en un campo conservativo externo establece que la suma de la entalpía total y el potencial externo es constante a lo largo de una línea de corriente .
En el caso habitual de un campo potencial pequeño, simplemente:
Forma de Friedmann y forma de Crocco
Sustituyendo el gradiente de presión por el gradiente de entropía y entalpía, según la primera ley de la termodinámica en la forma de entalpía:
En la forma convectiva de la ecuación de momento de Euler, se llega a:
Friedmann dedujo esta ecuación para el caso particular de un gas perfecto y la publicó en 1922. [15] Sin embargo, esta ecuación es general para un fluido no viscoso no conductor y no hay ninguna ecuación de estado implícita en ella.
Por otra parte, sustituyendo la forma entalpía de la primera ley de la termodinámica en la forma rotacional de la ecuación del momento de Euler, se obtiene:
y definiendo la entalpía total específica:
Se llega a la forma Crocco-Vazsonyi [16] (Crocco, 1937) de la ecuación del momento de Euler:
En el caso estable, las dos variables, entropía y entalpía total, son particularmente útiles ya que las ecuaciones de Euler pueden reformularse en la forma de Crocco:
Finalmente si el flujo también es isotérmico:
Definiendo la energía libre total específica de Gibbs :
La forma del Crocco se puede reducir a:
De estas relaciones se deduce que la energía libre total específica es uniforme en un flujo constante, irrotacional, isotérmico, isoentrópico y no viscoso.
Discontinuidades
Las ecuaciones de Euler son ecuaciones hiperbólicas cuasilineales y sus soluciones generales son ondas . Bajo ciertas suposiciones, pueden simplificarse y dar lugar a la ecuación de Burgers . Al igual que las conocidas olas oceánicas , las ondas descritas por las ecuaciones de Euler se "rompen" y se forman las llamadas ondas de choque ; este es un efecto no lineal y representa la solución que se vuelve multivaluada . Físicamente, esto representa una ruptura de las suposiciones que llevaron a la formulación de las ecuaciones diferenciales, y para extraer más información de las ecuaciones debemos volver a la forma integral más fundamental. Luego, las soluciones débiles se formulan trabajando en "saltos" (discontinuidades) en las cantidades de flujo (densidad, velocidad, presión, entropía) utilizando las ecuaciones de Rankine-Hugoniot . Las cantidades físicas rara vez son discontinuas; en flujos reales, estas discontinuidades se suavizan por la viscosidad y por la transferencia de calor . (Véase las ecuaciones de Navier-Stokes )
La propagación de choques se estudia, entre otros muchos campos, en la aerodinámica y la propulsión de cohetes , donde se producen flujos suficientemente rápidos.
Para calcular correctamente las cantidades continuas en zonas discontinuas (por ejemplo ondas de choque o capas límite) a partir de las formas locales [c] (todas las formas anteriores son formas locales, ya que las variables que se describen son típicas de un punto en el espacio considerado, es decir, son variables locales ) de las ecuaciones de Euler a través de métodos de diferencias finitas generalmente serían necesarios demasiados puntos espaciales y pasos de tiempo para la memoria de las computadoras ahora y en el futuro cercano. En estos casos es obligatorio evitar las formas locales de las ecuaciones de conservación, pasando algunas formas débiles , como la de volumen finito .
Ecuaciones de Rankine-Hugoniot
Partiendo del caso más simple, se considera una ecuación de conservación libre y estable en forma de conservación en el dominio espacial:
donde en general F es la matriz de flujo. Al integrar esta ecuación local sobre un volumen fijo V m , se obtiene:
Luego, basándonos en el teorema de divergencia , podemos transformar esta integral en una integral de borde del flujo:
Esta forma global simplemente establece que no hay flujo neto de una cantidad conservada que pase por una región en el caso de que sea constante y sin fuente. En 1D, el volumen se reduce a un intervalo , siendo su límite su extremo, entonces el teorema de divergencia se reduce al teorema fundamental del cálculo :
Esta es la ecuación de diferencias finitas simple , conocida como relación de salto :
Esto se puede hacer explícito así:
donde la notación empleada es:
O bien, si se realiza una integral indefinida:
Por otra parte, una ecuación de conservación transitoria:
trae a una relación de salto:
Para las ecuaciones de Euler unidimensionales las variables de conservación y el flujo son los vectores:
dónde:
- es el volumen específico,
- es el flujo de masa.
En el caso unidimensional las relaciones de salto correspondientes, llamadas ecuaciones de Rankine-Hugoniot , son:< [17]
En el caso unidimensional estable, se convierte simplemente en:
Gracias a la ecuación de diferencia de masa, la ecuación de diferencia de energía se puede simplificar sin ninguna restricción:
donde es la entalpía total específica.
Estas son las variables convectivas expresadas habitualmente:
dónde:
- es la velocidad del flujo
- es la energía interna específica.
La ecuación de energía es una forma integral de la ecuación de Bernoulli en el caso compresible. Las ecuaciones de masa y momento anteriores por sustitución conducen a la ecuación de Rayleigh:
Como el segundo término es una constante, la ecuación de Rayleigh siempre describe una línea simple en el plano de presión y volumen que no depende de ninguna ecuación de estado, es decir, la línea de Rayleigh. Mediante sustitución en las ecuaciones de Rankine-Hugoniot, esto también se puede hacer explícito como:
También se puede obtener la ecuación cinética y la ecuación de Hugoniot. Los pasajes analíticos no se muestran aquí por razones de brevedad.
Estos son respectivamente:
La ecuación de Hugoniot, acoplada a la ecuación fundamental de estado del material:
describe en general en el plano de presión-volumen una curva que pasa por las condiciones (v 0 , p 0 ), es decir la curva de Hugoniot, cuya forma depende fuertemente del tipo de material considerado.
También se acostumbra definir una función de Hugoniot : [18]
permitiendo cuantificar desviaciones de la ecuación de Hugoniot, de manera similar a la definición anterior de la carga hidráulica , útil para las desviaciones de la ecuación de Bernoulli.
Forma de volumen finito
Por otra parte, integrando una ecuación de conservación genérica:
en un volumen fijo V m , y luego basándose en el teorema de divergencia , se convierte en:
Integrando esta ecuación también sobre un intervalo de tiempo:
Ahora, definiendo la cantidad conservada del nodo:
Deducimos la forma de volumen finito:
En particular, para las ecuaciones de Euler, una vez determinadas las cantidades conservadas, las variables convectivas se deducen por sustitución hacia atrás:
Entonces las expresiones explícitas de volumen finito de las variables convectivas originales son: [19]
( forma de volumen finito )
Restricciones
Se ha demostrado que las ecuaciones de Euler no son un conjunto completo de ecuaciones, sino que requieren algunas restricciones adicionales para admitir una solución única: éstas son las ecuaciones de estado del material considerado. Para ser coherentes con la termodinámica, estas ecuaciones de estado deben satisfacer las dos leyes de la termodinámica. Por otra parte, por definición, los sistemas que no están en equilibrio se describen mediante leyes que se encuentran fuera de estas leyes. A continuación, enumeramos algunas ecuaciones de estado muy simples y su influencia correspondiente en las ecuaciones de Euler.
Gas politrópico ideal
Para un gas politrópico ideal la ecuación de estado fundamental es: [20]
donde es la energía específica, es el volumen específico, es la entropía específica, es la masa molecular, aquí se considera una constante ( proceso politrópico ), y se puede demostrar que corresponde a la relación de capacidad térmica . Se puede demostrar que esta ecuación es consistente con las ecuaciones de estado habituales empleadas por la termodinámica.
Según la definición termodinámica de temperatura:
Donde la temperatura se mide en unidades de energía. En primer lugar, observe que combinando estas dos ecuaciones se puede deducir la ley de los gases ideales :
o, en la forma habitual:
donde: es la densidad numérica del material. Por otra parte, la ley de los gases ideales es menos estricta que la ecuación de estado fundamental original considerada.
Consideremos ahora la capacidad calorífica molar asociada a un proceso x :
según la primera ley de la termodinámica:
Se puede expresar simplemente como:
Ahora, invirtiendo la ecuación para la temperatura T(e), deducimos que para un gas politrópico ideal la capacidad calorífica isocórica es una constante:
y de manera similar para un gas politrópico ideal la capacidad calorífica isobárica resulta constante:
Esto nos lleva a dos relaciones importantes entre las capacidades térmicas : la constante gamma representa en realidad la relación de capacidad térmica en el gas politrópico ideal:
Y también se llega a la relación de Meyer :
La energía específica es entonces, invirtiendo la relación T(e):
La entalpía específica resulta de la sustitución de esta última y de la ley de los gases ideales:
De esta ecuación se puede derivar la ecuación de presión por su definición termodinámica:
Invirtiéndola se llega a la ecuación mecánica de estado:
Entonces, para un gas ideal, las ecuaciones de Euler compresibles pueden expresarse simplemente en las variables mecánicas o primitivas volumen específico, velocidad de flujo y presión, tomando el conjunto de ecuaciones para un sistema termodinámico y modificando la ecuación de energía en una ecuación de presión a través de esta ecuación de estado mecánica. Por último, en forma convectiva resultan:
( forma convectiva ) [21]
y en forma cuasilineal unidimensional resultan:
donde la variable vectorial conservadora es:
y la matriz jacobiana correspondiente es: [22] [23]
Flujo constante en coordenadas de material
En el caso de flujo constante, es conveniente elegir el marco de Frenet-Serret a lo largo de una línea de corriente como sistema de coordenadas para describir la ecuación de Euler del momento constante: [24]
donde , y denotan la velocidad de flujo , la presión y la densidad , respectivamente.
Sea una base ortonormal de Frenet-Serret que consta de un vector unitario tangencial, un vector unitario normal y un vector unitario binormal a la línea de corriente, respectivamente. Como una línea de corriente es una curva que es tangente al vector de velocidad del flujo, el lado izquierdo de la ecuación anterior, la derivada convectiva de la velocidad, se puede describir de la siguiente manera: donde y es el radio de curvatura de la línea de corriente.
Por lo tanto, se descubre que la parte de momento de las ecuaciones de Euler para un flujo constante tiene una forma simple:
Para el flujo barotrópico , la ecuación de Bernoulli se deriva de la primera ecuación:
La segunda ecuación expresa que, en el caso de que la línea de corriente sea curva, debe existir un gradiente de presión normal a la línea de corriente porque la aceleración centrípeta de la parcela de fluido solo es generada por el gradiente de presión normal.
La tercera ecuación expresa que la presión es constante a lo largo del eje binormal.
Teorema de curvatura de línea de corriente
Sea la distancia desde el centro de curvatura de la línea de corriente, entonces la segunda ecuación se escribe de la siguiente manera:
dónde
Esta ecuación dice:
En un flujo constante de un fluido no viscoso sin fuerzas externas, el centro de curvatura de la línea de corriente se encuentra en la dirección de disminución de la presión radial.
Aunque esta relación entre el campo de presión y la curvatura del flujo es muy útil, no tiene un nombre en la literatura científica en idioma inglés. [25] Los especialistas en dinámica de fluidos japoneses llaman a la relación "teorema de curvatura de línea de corriente". [26]
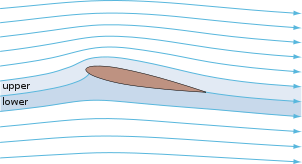
Este "teorema" explica claramente por qué hay presiones tan bajas en el centro de los vórtices [25] , que consisten en círculos concéntricos de líneas de corriente. Esta es también una manera de explicar intuitivamente por qué los perfiles aerodinámicos generan fuerzas de sustentación [25] .
Soluciones exactas
Todas las soluciones de flujo potencial son también soluciones de las ecuaciones de Euler, y en particular de las ecuaciones de Euler incompresibles cuando el potencial es armónico. [27]

Las soluciones de las ecuaciones de Euler con vorticidad son:
- flujos de corte paralelos : donde el flujo es unidireccional y la velocidad del flujo solo varía en las direcciones de flujo transversal, por ejemplo, en un sistema de coordenadas cartesianas, el flujo es, por ejemplo, en la dirección -, con el único componente de velocidad distinto de cero que solo depende de y y no de [28]
- Flujo de Arnold-Beltrami-Childress : una solución exacta de las ecuaciones de Euler incompresibles.
- Gibbon, Moore y Stuart presentaron en 2003 dos soluciones de las ecuaciones de Euler tridimensionales con simetría cilíndrica. [29] Estas dos soluciones tienen energía infinita; explotan en todas partes en el espacio en un tiempo finito.
Véase también
- Teorema de Bernoulli
- Teorema de circulación de Kelvin
- Ecuaciones de Cauchy
- Número de Froude
- Ecuaciones de Madelung
- Ecuaciones de Navier-Stokes
- Ecuación de hamburguesas
- Ecuaciones de jeans
- Fluido perfecto
- La paradoja de D'Alembert
Referencias
Notas
- ^ En 3D, por ejemplo , tiene longitud 5, tiene tamaño 3×3 y tiene tamaño 5×3, por lo que las formas explícitas son:
- ^ En 3D, por ejemplo, y tiene una longitud de 5, I tiene un tamaño de 3×3 y F tiene un tamaño de 3×5, por lo que las formas explícitas son:
- ^ A veces, las formas local y global también se denominan respectivamente diferencial y no diferencial , pero esto no es apropiado en todos los casos. Por ejemplo, esto es apropiado para las ecuaciones de Euler, mientras que no lo es para las ecuaciones de Navier-Stokes, ya que en su forma global hay algunos operadores derivados espaciales de primer orden residuales en todos los términos de transporte característicos que en la forma local contienen derivadas espaciales de segundo orden.
Citas
- ^ abcd Toro 1999, pág. 24.
- ^ Anderson 1995.
- ^ Euler 1757.
- ^ por Christodoulou 2007.
- ^ Darrigol, O.; Frisch, U. (2008). "De la mecánica de Newton a las ecuaciones de Euler". Physica D: Nonlinear Phenomena . 237 (14–17): 1855–1869. doi :10.1016/j.physd.2007.08.003.
- ^ desde Hunter 2006.
- ^ Elgindi, Tarek M. (1 de noviembre de 2021). "Formación de singularidades en tiempo finito para soluciones $C^{1,\alpha}$ de las ecuaciones de Euler incompresibles en $\mathbb{R}^3$". Anales de Matemáticas . 194 (3). arXiv : 1904.04795 . doi :10.4007/annals.2021.194.3.2. ISSN 0003-486X.
- ^ Cuartapelle y Auteri 2013, pag. 13, cap. 9.
- ^ Landau y Lifshitz 2013, pág. 4, ecuaciones 2.6 y 2.7.
- ^ Henderson 2000, pág. 152, 2.6 Propiedades termodinámicas de los materiales.
- ^ Chorin y Marsden 2013, pag. 118, párr. 3.2 Choques.
- ^ Toro 1999, p. 44, par 2.1 Ecuaciones cuasi-lineales.
- ^ Toro 1999, p. 52, par 2.3 Sistema hiperbólico lineal.
- ^ Valorani y Nasuti nd, págs. 11-12.
- ^ Friedmann 1934, pág. 198, ecuación 91.
- ^ Henderson 2000, pag. 177, párr. 2.12 Teorema de Crocco.
- ^ Chorin y Marsden 2013, pag. 122, párr. 3.2 Choques.
- ^ Henderson 2000, pág. 167, párrafo 2.96 El teorema de Bethe-Weyl.
- ^ Cuartapelle y Auteri 2013, pag. 161, párr. 11.10: Forma diferencial: metodo dei volumi finiti.
- ^ Cuartapelle y Auteri 2013, pag. A-61, Apéndice E.
- ^ Toro 1999, p. 91, par 3.1.2 Formulaciones no conservadoras.
- ^ Zingale 2013.
- ^ Toro 1999, pág. 92.
- ^ Fay 1994, págs. 150-152.
- ^ abcBabinsky 2003.
- ^ Imai 1973.
- ^ Marchioro y Pulvirenti 1994, pag. 33.
- ^ Friedlander y Serre 2003, pág. 298.
- ^ Gibbon, Moore y Stuart 2003.
Fuentes
- Anderson, John (1995). Dinámica de fluidos computacional. McGraw-Hill Education. ISBN 978-0-07-001685-9.
- Babinsky, Holger (noviembre de 2003), "¿Cómo funcionan las alas?" (PDF) , Physics Education , 38 (6): 497–503, Bibcode :2003PhyEd..38..497B, doi :10.1088/0031-9120/38/6/001, S2CID 1657792
- Chorin, Alexandre J.; Marsden, Jerrold E. (2013). Introducción matemática a la mecánica de fluidos. Springer. ISBN 978-1-4612-0883-9.
- Christodoulou, Demetrios (octubre de 2007). "Las ecuaciones de Euler del flujo de fluidos compresibles" (PDF) . Boletín de la Sociedad Americana de Matemáticas . 44 (4): 581–602. doi : 10.1090/S0273-0979-07-01181-0 .
- Euler, Leonhard (1757). "Principes généraux du mouvement des fluides" [Principios generales del movimiento de fluidos]. Mémoires de l'académie des sciences de Berlin (en francés). 11 : 274–315.
- Fay, James A. (1994). Introducción a la mecánica de fluidos. MIT Press. ISBN 978-0-262-06165-0.
- Friedlander, S.; Serre, D., eds. (2003). Manual de dinámica de fluidos matemática – Volumen 2. Elsevier. ISBN 978-0-444-51287-1.
- Friedmann, A. (1934) [1922]. Kochin, Nikolai (ed.). Опыт гидромеханики сжимаемой жидкости [ Ensayo sobre hidrodinámica de fluidos compresibles ] (en ruso). Petrogrado .
{{cite book}}: CS1 maint: location missing publisher (link) - Gibbon, JD; Moore, DR; Stuart, JT (2003). "Soluciones exactas, de energía infinita y de explosión de las ecuaciones de Euler tridimensionales". No linealidad . 16 (5): 1823–1831. Bibcode :2003Nonli..16.1823G. doi :10.1088/0951-7715/16/5/315. S2CID 250797052.
- Henderson, LF (2000). "Leyes generales para la propagación de ondas de choque a través de la materia". En Ben-Dor, Gabi; Igra, Ozer; Elperin, Tov (eds.). Manual de ondas de choque, conjunto de tres volúmenes . Elsevier. ISBN 978-0-08-053372-8.
- Hunter, John K. (25 de septiembre de 2006), Introducción a las ecuaciones de Euler incompresibles (PDF) , consultado el 31 de mayo de 2019
- 今井 功 (IMAI, Isao) (noviembre de 1973). 『流体力学(前編)』 [ Dinámica de fluidos 1 ] (en japonés). 裳華房 (Shoukabou). ISBN 4-7853-2314-0.
- Landau, LD; Lifshitz, EM (2013). Mecánica de fluidos. Elsevier. ISBN 978-1-4831-4050-6.
- Marchioro, C.; Pulvirenti, M. (1994). Teoría matemática de fluidos no viscosos incompresibles . Applied Mathematical Sciences. Vol. 96. Nueva York: Springer. ISBN 0-387-94044-8.
- Cuartapelle, Luigi; Auteri, Franco (2013). Fluidodinamica comprimibile [ Dinámica de fluidos compresibles ] (en italiano). CEA. ISBN 978-88-08-18558-7.
- Toro, EF (1999). Solucionadores de Riemann y métodos numéricos para dinámica de fluidos: una introducción práctica. Springer. ISBN 978-3-540-65966-2.
- Valorani, Mauro; Nasuti, Francesco (sin fecha), Metodi di analisi delle turbomacchine (PDF) , Sapienza - Universit`a di Roma, archivado desde el original (PDF) el 16 de mayo de 2022 , consultado el 31 de mayo de 2019 .
- Zingale, M. (16 de abril de 2013), Notas sobre las ecuaciones de Euler (PDF) , archivado desde el original (PDF) el 19 de junio de 2015 , consultado el 31 de mayo de 2019
Lectura adicional
- Badin, G.; Crisciani, F. (2018). Formulación variacional de la dinámica de fluidos y de fluidos geofísicos - Mecánica, simetrías y leyes de conservación - . Springer. p. 218. Bibcode :2018vffg.book.....B. doi :10.1007/978-3-319-59695-2. ISBN 978-3-319-59694-5.S2CID125902566 .
- Batchelor, GK (1967). Introducción a la dinámica de fluidos . Cambridge University Press. ISBN 0-521-66396-2.
- Thompson, Philip A. (1972). Flujo de fluidos compresibles . Nueva York: McGraw-Hill. ISBN 0-07-064405-5.



























![{\displaystyle {\begin{aligned}u^{*}&\equiv {\frac {u}{u_{0}}},&r^{*}&\equiv {\frac {r}{r_{0}}},\\[5pt]t^{*}&\equiv {\frac {u_{0}}{r_{0}}}t,&p^{*}&\equiv {\frac {w}{u_{0}^{2}}},\\[5pt]\nabla ^{*}&\equiv r_{0}\nabla .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff224d97926a5e5ef7fd2b56faf15d9acfce43d3)






























![{\displaystyle {\begin{aligned}{D\rho \over Dt}&=-\rho \nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt }}&=-{\frac {\nabla p}{\rho }}+\mathbf {g} \\[1.2ex]{De \over Dt}&=-{\frac {p}{\rho }} \nabla \cdot \mathbf {u} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32d0d7ac47e299fea99a042809f6c3a158849ea5)

![{\displaystyle {\begin{aligned}{\partial \rho \over \partial t}+\mathbf {u} \cdot \nabla \rho +\rho \nabla \cdot \mathbf {u} &=0,\\ [1.2ex]{\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \nabla \mathbf {u} +{\frac {\nabla p}{\rho } }&=\mathbf {g} ,\\[1.2ex]{\partial e \over \partial t}+\mathbf {u} \cdot \nabla e+{\frac {p}{\rho }}\nabla \ cdot \mathbf {u} &=0.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95297ee2f1df5469842b64256df3d7c20f9e580b)


















![{\displaystyle {\begin{aligned}{Dv \sobre Dt}&=v\nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&=ve_{vv}\nabla v+ve_{vs}\nabla s+\mathbf {g} \\[1.2ex]{Ds \sobre Dt}&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f310b199bfe2b79f06833b233ce336a60d1d1ca3)


















![{\displaystyle \mathbf {P} =\left[\mathbf {p} _{1},\mathbf {p} _{2},...,\mathbf {p} _{n}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2550bf598e0812e8b9a63edbf9c5f2b126fb3d3)





![{\displaystyle {\begin{aligned}{\partial v \sobre \parcial t}+u{\partial v \sobre \parcial x}-v{\partial u \sobre \parcial x}&=0,\\[1.2ex]{\partial u \sobre \parcial t}+u{\partial u \sobre \parcial x}-e_{vv}v{\partial v \sobre \parcial x}-e_{vs}v{\partial s \sobre \parcial x}&=0,\\[1.2ex]{\partial s \sobre \parcial t}+u{\partial s \sobre \parcial x}&=0.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b241849d843555ab4577a4ec1ef747e3cebf6e6)










![{\displaystyle \left\{{\begin{aligned}e_{vv}&>0\\[1.2ex]e_{vv}e_{ss}-e_{vs}^{2}&>0\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c95b8e89f2d859f01c14c0697d666b320d599fe)
































































![{\displaystyle {\begin{aligned}{\frac {dx}{dt}}\Delta \left({\frac {1}{v}}\right)&=\Delta j,\\[1.2ex]{\frac {dx}{dt}}\Delta j&=\Delta (vj^{2}+p),\\[1.2ex]{\frac {dx}{dt}}\Delta E^{t}&=\Delta (jv(E^{t}+p)).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71a7abf0a7c915e526c4faf0bcefe77b953e68df)
![{\displaystyle {\begin{aligned}\Delta j&=0,\\[1.2ex]\Delta \left(vj^{2}+p\right)&=0,\\[1.2ex]\Delta \left(j\left({\frac {E^{t}}{\rho }}+{\frac {p}{\rho }}\right)\right)&=0.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a9ad85a62913807b4ef90497c7e84086ceb802c)
![{\displaystyle {\begin{aligned}\Delta j&=0,\\[1.2ex]\Delta \left(vj^{2}+p\right)&=0,\\[1.2ex]\Delta h^{t}&=0,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b81849f6194606a6a227deade45b12160bc1def9)

![{\displaystyle {\begin{aligned}\Delta j&=0,\\[1.2ex]\Delta \left({\frac {u^{2}}{v}}+p\right)&=0,\\[1.2ex]\Delta \left(e+{\frac {1}{2}}u^{2}+pv\right)&=0,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7409e3ac85617c868ff0dca40d390446c54644ed)

![{\displaystyle {\begin{aligned}\rho u&=\rho _{0}u_{0},\\[1.2ex]\rho u^{2}+p&=\rho _{0}u_{0}^{2}+p_{0},\\[1.2ex]e+{\frac {1}{2}}u^{2}+{\frac {p}{\rho }}&=e_{0}+{\frac {1}{2}}u_{0}^{2}+{\frac {p_{0}}{\rho _{0}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52a09a9c7979488e16a4f471ba46be350ecb92e8)
![{\displaystyle {\begin{aligned}u^{2}(v,p)&=u_{0}^{2}+(p-p_{0})(v_{0}+v),\\[1.2ex]e(v,p)&=e_{0}+{\tfrac {1}{2}}(p+p_{0})(v_{0}-v).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d36bacbb883db170642d029cec3372551ceb55)







![{\displaystyle {\begin{aligned}\displaystyle \mathbf {u} _{m,n}&={\frac {\mathbf {j} _{m,n}}{\rho _{m,n}}},\\[1.2ex]\displaystyle e_{m,n}&={\frac {E_{m,n}^{t}}{\rho _{m,n}}}-{\frac {1}{2}}u_{m,n}^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66185f9a053d04e38a028130363d9257646e53a0)
![{\displaystyle {\begin{aligned}\rho _{m,n+1}&=\rho _{m,n}-{\frac {1}{V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}\rho \mathbf {u} \cdot {\hat {n}}\,ds\,dt\\[1.2ex]\mathbf {u} _{m,n+1}&=\mathbf {u} _{m,n}-{\frac {1}{\rho _{m,n}V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}(\rho \mathbf {u} \otimes \mathbf {u} -p\mathbf {I} )\cdot {\hat {n}}\,ds\,dt\\[1.2ex]\mathbf {e} _{m,n+1}&=\mathbf {e} _{m,n}-{\frac {1}{2}}\left(u_{m,n+1}^{2}-u_{m,n}^{2}\right)-{\frac {1}{\rho _{m,n}V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}\left(\rho e+{\frac {1}{2}}\rho u^{2}+p\right)\mathbf {u} \cdot {\hat {n}}\,ds\,dt\\[1.2ex]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a765370d1e2f051e4cb6fcdfab1fd0158f327ab)


















![{\displaystyle {\begin{aligned}{Dv \over Dt}&=v\nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&= v\nabla p+\mathbf {g} \\[1.2ex]{Dp \over Dt}&=-\gamma p\nabla \cdot \mathbf {u} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aecf22f23701bb253eabf2c8ee558f5713f4e2b)





















