Ecuación de continuidad

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Ecuación de continuidad» – noticias  · periódicos  · libros  · académico  · JSTOR ( diciembre de 2023 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Parte de una serie sobre
Mecánica de medios continuos
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ Leyes de difusión de Fick
Leyes Conservaciones Masa Impulso Energía Desigualdades Clausius-Duhem (entropía)
Mecánica de sólidos Deformación Elasticidad lineal Plasticidad Ley de Hooke Estrés Cepa Deformación finita Deformación infinitesimal Compatibilidad Doblado Mecánica de contacto friccional Teoría de la falla del material Mecánica de fracturas
Mecánica de fluidos Fluidos Estática  · Dinámica Principio de Arquímedes  · Principio de Bernoulli Ecuaciones de Navier-Stokes Ecuación de Poiseuille  · Ley de Pascal Viscosidad ( Newtoniano  · no newtoniano ) Flotabilidad  · Mezcla  · Presión Líquidos Adhesión Acción capilar Cromatografía Cohesión (química) Tensión superficial Gases Atmósfera Ley de Boyle Ley de Charles Ley combinada de los gases Ley de Fick Ley de Gay-Lussac Ley de Graham Plasma
Reología Viscoelasticidad Reometría Rheometer Smart fluids Electrorheological Magnetorheological Ferrofluids
Scientists Bernoulli Boyle Cauchy Charles Euler Fick Gay-Lussac Graham Hooke Newton Navier Noll Pascal Stokes Truesdell
v t e

Una ecuación de continuidad o ecuación de transporte es una ecuación que describe el transporte de alguna cantidad. Es particularmente simple y poderosa cuando se aplica a una cantidad conservada , pero se puede generalizar para aplicarla a cualquier cantidad extensiva . Dado que la masa , la energía , el momento , la carga eléctrica y otras cantidades naturales se conservan en sus respectivas condiciones apropiadas, se pueden describir diversos fenómenos físicos utilizando ecuaciones de continuidad.

Las ecuaciones de continuidad son una forma local más fuerte de las leyes de conservación . Por ejemplo, una versión débil de la ley de conservación de la energía establece que la energía no se puede crear ni destruir, es decir, la cantidad total de energía en el universo es fija. Esta afirmación no descarta la posibilidad de que una cantidad de energía pueda desaparecer de un punto mientras aparece simultáneamente en otro punto. Una afirmación más fuerte es que la energía se conserva localmente : la energía no se puede crear ni destruir, ni puede " teletransportarse " de un lugar a otro; solo puede moverse mediante un flujo continuo. Una ecuación de continuidad es la forma matemática de expresar este tipo de afirmación. Por ejemplo, la ecuación de continuidad para la carga eléctrica establece que la cantidad de carga eléctrica en cualquier volumen del espacio solo puede cambiar por la cantidad de corriente eléctrica que fluye hacia adentro o hacia afuera de ese volumen a través de sus límites.

En términos más generales, las ecuaciones de continuidad pueden incluir términos de "fuente" y "sumidero", que les permiten describir cantidades que a menudo, aunque no siempre, se conservan, como la densidad de una especie molecular que puede crearse o destruirse mediante reacciones químicas. En un ejemplo cotidiano, existe una ecuación de continuidad para la cantidad de personas vivas; tiene un "término de fuente" para dar cuenta de las personas que nacen y un "término de sumidero" para dar cuenta de las personas que mueren.

Cualquier ecuación de continuidad puede expresarse en una "forma integral" (en términos de una integral de flujo ), que se aplica a cualquier región finita, o en una "forma diferencial" (en términos del operador de divergencia ), que se aplica en un punto.

Las ecuaciones de continuidad sustentan ecuaciones de transporte más específicas, como la ecuación de convección-difusión , la ecuación de transporte de Boltzmann y las ecuaciones de Navier-Stokes .

Los flujos regidos por ecuaciones de continuidad se pueden visualizar utilizando un diagrama de Sankey .

Una ecuación de continuidad es útil cuando se puede definir un flujo . Para definir el flujo, primero debe haber una cantidad q que pueda fluir o moverse, como masa , energía , carga eléctrica , momento , número de moléculas, etc. Sea ρ la densidad de volumen de esta cantidad, es decir, la cantidad de q por unidad de volumen.

La forma en que fluye esta cantidad q se describe mediante su flujo. El flujo de q es un campo vectorial , que denotamos como j . A continuación se presentan algunos ejemplos y propiedades del flujo:

• La dimensión del flujo es "cantidad de q que fluye por unidad de tiempo, a través de una unidad de área". Por ejemplo, en la ecuación de continuidad de masa para el agua que fluye, si 1 gramo por segundo de agua fluye a través de una tubería con un área de sección transversal de 1 cm2 ^, entonces el flujo de masa promedio j dentro de la tubería es (1 g/s)/cm2 ^, y su dirección es a lo largo de la tubería en la dirección en la que fluye el agua. Fuera de la tubería, donde no hay agua, el flujo es cero.
• Si existe un campo de velocidad u que describe el flujo relevante (en otras palabras, si toda la cantidad q en un punto x se mueve con velocidad u ( x )) , entonces el flujo es por definición igual a la densidad multiplicada por el campo de velocidad:

$${\displaystyle \mathbf {j} =\rho \mathbf {u} }$$

Por ejemplo, si en la ecuación de continuidad de masa para el agua que fluye, u es la velocidad del agua en cada punto y ρ es la densidad del agua en cada punto, entonces j sería el flujo de masa, también conocido como descarga de material .

• En un ejemplo bien conocido, el flujo de carga eléctrica es la densidad de corriente eléctrica .

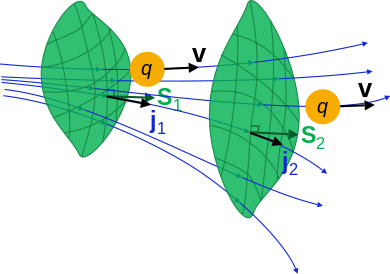
• Si existe una superficie imaginaria S , entonces la integral de superficie del flujo sobre S es igual a la cantidad de q que pasa a través de la superficie S por unidad de tiempo:

en el que es una integral de superficie .${\textstyle \iint _{S}d\mathbf {S} }$

(Tenga en cuenta que el concepto que aquí se denomina "flujo" se denomina alternativamente densidad de flujo en alguna literatura, en cuyo contexto "flujo" denota la integral de superficie de la densidad de flujo. Consulte el artículo principal sobre Flujo para obtener más detalles).

La forma integral de la ecuación de continuidad establece que:

• La cantidad de q en una región aumenta cuando fluye q adicional hacia adentro a través de la superficie de la región, y disminuye cuando fluye hacia afuera;
• La cantidad de q en una región aumenta cuando se crea q nuevo dentro de la región y disminuye cuando se destruye q ;
• Aparte de estos dos procesos, no hay otra forma de que cambie la cantidad de q en una región.

Matemáticamente, la forma integral de la ecuación de continuidad que expresa la tasa de aumento de q dentro de un volumen V es:

dónde

• S es cualquier superficie imaginaria cerrada , que encierra un volumen V ,
• ${\displaystyle \oint _{S}d\mathbf {S} }$denota una integral de superficie sobre esa superficie cerrada,
• q es la cantidad total de la cantidad en el volumen V ,
• j es el flujo de q ,
• Es hora,
• Σ es la tasa neta a la que se genera q dentro del volumen V por unidad de tiempo. Cuando se genera q , se denomina fuente de q y hace que Σ sea más positivo. Cuando se destruye q , se denomina sumidero de q y hace que Σ sea más negativo. Este término a veces se escribe como o el cambio total de q desde su generación o destrucción dentro del volumen de control.${\displaystyle dq/dt|_{\text{gen}}}$

En un ejemplo sencillo, V podría ser un edificio y q podría ser el número de personas que hay en el edificio. La superficie S estaría formada por las paredes, las puertas, el techo y los cimientos del edificio. Entonces, la ecuación de continuidad establece que el número de personas que hay en el edificio aumenta cuando las personas entran en el edificio (un flujo hacia adentro a través de la superficie), disminuye cuando las personas salen del edificio (un flujo hacia afuera a través de la superficie), aumenta cuando alguien en el edificio da a luz (una fuente, Σ > 0 ), y disminuye cuando alguien en el edificio muere (un sumidero, Σ < 0 ).

Por el teorema de divergencia , una ecuación de continuidad general también puede escribirse en "forma diferencial":

dónde

• ∇⋅ es divergencia ,
• ρ es la densidad de la cantidad q (es decir, la cantidad q por unidad de volumen),
• j es la densidad de flujo de q (es decir, j = ρ v , donde v es el campo vectorial que describe el movimiento de la cantidad q ),
• Es hora,
• σ es la generación de q por unidad de volumen por unidad de tiempo. Los términos que generan q (es decir, σ > 0 ) o eliminan q (es decir, σ < 0 ) se denominan "fuentes" y "sumideros", respectivamente.

Esta ecuación general se puede utilizar para derivar cualquier ecuación de continuidad, desde la más simple, como la ecuación de continuidad de volumen, hasta la más complicada, como las ecuaciones de Navier-Stokes . Esta ecuación también generaliza la ecuación de advección . Otras ecuaciones de la física, como la ley de Gauss del campo eléctrico y la ley de Gauss de la gravedad , tienen una forma matemática similar a la ecuación de continuidad, pero no suelen denominarse con el término "ecuación de continuidad", porque j en esos casos no representa el flujo de una cantidad física real.

En el caso de que q sea una cantidad conservada que no se puede crear ni destruir (como la energía ), σ = 0 y las ecuaciones se convierten en:$${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =0}$$

En la teoría electromagnética , la ecuación de continuidad es una ley empírica que expresa la conservación de la carga (local) . Matemáticamente es una consecuencia automática de las ecuaciones de Maxwell , aunque la conservación de la carga es más fundamental que las ecuaciones de Maxwell. Establece que la divergencia de la densidad de corriente J (en amperios por metro cuadrado) es igual a la tasa negativa de cambio de la densidad de carga ρ (en culombios por metro cúbico),$${\displaystyle \nabla \cdot \mathbf {J} =-{\frac {\partial \rho }{\partial t}}}$$

La corriente es el movimiento de carga. La ecuación de continuidad dice que si la carga se mueve fuera de un volumen diferencial (es decir, la divergencia de la densidad de corriente es positiva), entonces la cantidad de carga dentro de ese volumen va a disminuir, por lo que la tasa de cambio de la densidad de carga es negativa. Por lo tanto, la ecuación de continuidad equivale a una conservación de carga.

Si existieran monopolos magnéticos , también habría una ecuación de continuidad para las corrientes monopolares; consulte el artículo sobre monopolos para conocer los antecedentes y la dualidad entre las corrientes eléctricas y magnéticas.

En dinámica de fluidos , la ecuación de continuidad establece que la velocidad a la que la masa ingresa a un sistema es igual a la velocidad a la que la masa sale del sistema más la acumulación de masa dentro del sistema. ^{[1] [2]} La forma diferencial de la ecuación de continuidad es: ^[1] donde$${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {u} )=0}$$

• ρ es la densidad del fluido ,
• Es hora,
• u es el campo vectorial de velocidad de flujo .

La derivada temporal puede entenderse como la acumulación (o pérdida) de masa en el sistema, mientras que el término de divergencia representa la diferencia entre el flujo entrante y el saliente. En este contexto, esta ecuación también es una de las ecuaciones de Euler (dinámica de fluidos) . Las ecuaciones de Navier-Stokes forman una ecuación de continuidad vectorial que describe la conservación del momento lineal .

Si el fluido es incompresible (la tasa de deformación volumétrica es cero), la ecuación de continuidad de masa se simplifica a una ecuación de continuidad de volumen: ^[3] lo que significa que la divergencia del campo de velocidad es cero en todas partes. Físicamente, esto es equivalente a decir que la tasa de dilatación del volumen local es cero, por lo tanto, un flujo de agua a través de una tubería convergente se ajustará únicamente aumentando su velocidad ya que el agua es en gran medida incompresible.$${\displaystyle \nabla \cdot \mathbf {u} =0,}$$

En la visión artificial , el flujo óptico es el patrón de movimiento aparente de los objetos en una escena visual. Suponiendo que el brillo del objeto en movimiento no cambia entre dos fotogramas de la imagen, se puede derivar la ecuación del flujo óptico como: ^{[ cita requerida ]} donde$${\displaystyle {\frac {\partial I}{\partial x}}V_{x}+{\frac {\partial I}{\partial y}}V_{y}+{\frac {\partial I}{\partial t}}=\nabla I\cdot \mathbf {V} +{\frac {\partial I}{\partial t}}=0}$$

• Es hora,
• coordenadas x , y en la imagen,
• I es la intensidad de la imagen en la coordenada de la imagen ( x , y ) y el tiempo t ,
• V es el vector de velocidad del flujo ópticoen la coordenada de la imagen ( x , y ) y el tiempo t${\displaystyle (V_{x},V_{y})}$

La conservación de la energía dice que la energía no se crea ni se destruye. (Véase más abajo los matices asociados a la relatividad general). Por lo tanto, existe una ecuación de continuidad para el flujo de energía: donde$${\displaystyle {\frac {\partial u}{\partial t}}+\nabla \cdot \mathbf {q} =0}$$

• u , densidad de energía local(energía por unidad de volumen),
• q , flujo de energía (transferencia de energía por unidad de área transversal por unidad de tiempo) como vector,

Un ejemplo práctico importante es el flujo de calor . Cuando el calor fluye dentro de un sólido, la ecuación de continuidad se puede combinar con la ley de Fourier (el flujo de calor es proporcional al gradiente de temperatura) para llegar a la ecuación del calor . La ecuación del flujo de calor también puede tener términos fuente: Aunque la energía no se puede crear ni destruir, el calor se puede crear a partir de otros tipos de energía, por ejemplo, mediante la fricción o el calentamiento Joule .

Si hay una cantidad que se mueve continuamente según un proceso estocástico (aleatorio), como la ubicación de una única molécula disuelta con movimiento browniano , entonces existe una ecuación de continuidad para su distribución de probabilidad . El flujo en este caso es la probabilidad por unidad de área por unidad de tiempo de que la partícula pase a través de una superficie. Según la ecuación de continuidad, la divergencia negativa de este flujo es igual a la tasa de cambio de la densidad de probabilidad . La ecuación de continuidad refleja el hecho de que la molécula siempre está en algún lugar (la integral de su distribución de probabilidad siempre es igual a 1) y que se mueve mediante un movimiento continuo (sin teletransportarse ).

La mecánica cuántica es otro campo en el que existe una ecuación de continuidad relacionada con la conservación de la probabilidad . Los términos de la ecuación requieren las siguientes definiciones y son un poco menos obvios que los otros ejemplos anteriores, por lo que se describen a continuación:

• La función de onda Ψ para una sola partícula en el espacio de posición (en lugar de en el espacio de momento ), es decir, una función de la posición r y el tiempo t , Ψ = Ψ( r , t ) .
• La función de densidad de probabilidad es$${\displaystyle \rho (\mathbf {r} ,t)=\Psi ^{*}(\mathbf {r} ,t)\Psi (\mathbf {r} ,t)=|\Psi (\mathbf {r} ,t)|^{2}.}$$
• La probabilidad de encontrar la partícula dentro de V en t se denota y define por$${\displaystyle P=P_{\mathbf {r} \in V}(t)=\int _{V}\Psi ^{*}\Psi dV=\int _{V}|\Psi |^{2}dV.}$$
• La corriente de probabilidad (flujo de probabilidad) es$${\displaystyle \mathbf {j} (\mathbf {r} ,t)={\frac {\hbar }{2mi}}\left[\Psi ^{*}\left(\nabla \Psi \right)-\Psi \left(\nabla \Psi ^{*}\right)\right].}$$

Con estas definiciones la ecuación de continuidad queda así:$${\displaystyle \nabla \cdot \mathbf {j} +{\frac {\partial \rho }{\partial t}}=0\mathrel {\rightleftharpoons } \nabla \cdot \mathbf {j} +{\frac {\partial |\Psi |^{2}}{\partial t}}=0.}$$

Se puede citar cualquiera de las dos formas. Intuitivamente, las cantidades anteriores indican que esto representa el flujo de probabilidad. La probabilidad de encontrar la partícula en alguna posición r y tiempo t fluye como un fluido ; de ahí el término corriente de probabilidad , un campo vectorial . La partícula en sí no fluye de manera determinista en este campo vectorial .

El flujo de corriente total en el semiconductor consiste en la corriente de deriva y la corriente de difusión tanto de los electrones en la banda de conducción como de los huecos en la banda de valencia.

Forma general para electrones en una dimensión: donde:$${\displaystyle {\frac {\partial n}{\partial t}}=n\mu _{n}{\frac {\partial E}{\partial x}}+\mu _{n}E{\frac {\partial n}{\partial x}}+D_{n}{\frac {\partial ^{2}n}{\partial x^{2}}}+(G_{n}-R_{n})}$$

• n es la concentración local de electrones
• ${\displaystyle \mu _{n}}$¿Es la movilidad electrónica?
• E es el campo eléctrico a través de la región de agotamiento
• D _n es el coeficiente de difusión de los electrones.
• G _n es la tasa de generación de electrones
• R _n es la tasa de recombinación de electrones

De manera similar, para los agujeros: donde:$${\displaystyle {\frac {\partial p}{\partial t}}=-p\mu _{p}{\frac {\partial E}{\partial x}}-\mu _{p}E{\frac {\partial p}{\partial x}}+D_{p}{\frac {\partial ^{2}p}{\partial x^{2}}}+(G_{p}-R_{p})}$$

• p es la concentración local de agujeros
• ${\displaystyle \mu _{p}}$¿Es la movilidad del agujero?
• E es el campo eléctrico a través de la región de agotamiento
• D _p es el coeficiente de difusión de los huecos
• G _p es la tasa de generación de agujeros
• R _p es la tasa de recombinación de agujeros

En esta sección se presenta una derivación de la ecuación anterior para los electrones. Se puede encontrar una derivación similar para la ecuación para los huecos.

Consideremos el hecho de que el número de electrones se conserva en un volumen de material semiconductor con área de sección transversal, A , y longitud, dx , a lo largo del eje x . Más precisamente, se puede decir:$${\displaystyle {\text{Rate of change of electron density}}=({\text{Electron flux in}}-{\text{Electron flux out}})+{\text{Net generation inside a volume}}}$$

Matemáticamente, esta igualdad se puede escribir: Aquí J denota la densidad de corriente (cuya dirección es contraria al flujo de electrones por convención) debido al flujo de electrones dentro del volumen considerado del semiconductor. También se denomina densidad de corriente de electrones.$${\displaystyle {\begin{aligned}{\frac {dn}{dt}}A\,dx&=\left[J(x+dx)-J(x)\right]{\frac {A}{e}}+(G_{n}-R_{n})A\,dx\\&=\left[J(x)+{\frac {dJ}{dx}}dx-J(x)\right]{\frac {A}{e}}+(G_{n}-R_{n})A\,dx\\[1.2ex]{\frac {dn}{dt}}&={\frac {1}{e}}{\frac {dJ}{dx}}+(G_{n}-R_{n})\end{aligned}}}$$

La densidad de corriente total de electrones es la suma de las densidades de corriente de deriva y de corriente de difusión:$${\displaystyle J_{n}=en\mu _{n}E+eD_{n}{\frac {dn}{dx}}}$$

Por lo tanto, tenemos$${\displaystyle {\frac {dn}{dt}}={\frac {1}{e}}{\frac {d}{dx}}\left(en\mu _{n}E+eD_{n}{\frac {dn}{dx}}\right)+(G_{n}-R_{n})}$$

La aplicación de la regla del producto da como resultado la expresión final:$${\displaystyle {\frac {dn}{dt}}=\mu _{n}E{\frac {dn}{dx}}+\mu _{n}n{\frac {dE}{dx}}+D_{n}{\frac {d^{2}n}{dx^{2}}}+(G_{n}-R_{n})}$$

La clave para resolver estas ecuaciones en dispositivos reales es, siempre que sea posible, seleccionar regiones en las que la mayoría de los mecanismos sean despreciables para que las ecuaciones se reduzcan a una forma mucho más simple.

La notación y las herramientas de la relatividad especial , especialmente los 4 vectores y los 4 gradientes , ofrecen una forma conveniente de escribir cualquier ecuación de continuidad.

La densidad de una cantidad ρ y su corriente j se pueden combinar en un 4-vector llamado 4-corriente : donde c es la velocidad de la luz . La 4- divergencia de esta corriente es: donde ∂ _μ es el 4-gradiente y μ es un índice que etiqueta la dimensión del espacio-tiempo . Entonces la ecuación de continuidad es: en el caso habitual en el que no hay fuentes ni sumideros, es decir, para cantidades perfectamente conservadas como la energía o la carga. Esta ecuación de continuidad es manifiestamente ("obviamente") invariante de Lorentz .$${\displaystyle J=\left(c\rho ,j_{x},j_{y},j_{z}\right)}$$$${\displaystyle \partial _{\mu }J^{\mu }=c{\frac {\partial \rho }{\partial ct}}+\nabla \cdot \mathbf {j} }$$ $${\displaystyle \partial _{\mu }J^{\mu }=0}$$

Ejemplos de ecuaciones de continuidad a menudo escritas en esta forma incluyen la conservación de carga eléctrica , donde J es la 4-corriente eléctrica ; y la conservación de energía-momento , donde T es el tensor de tensión-energía .$${\displaystyle \partial _{\mu }J^{\mu }=0}$$$${\displaystyle \partial _{\nu }T^{\mu \nu }=0}$$

En la relatividad general , donde el espacio-tiempo es curvo, la ecuación de continuidad (en forma diferencial) para la energía, la carga u otras cantidades conservadas implica la divergencia covariante en lugar de la divergencia ordinaria.

Por ejemplo, el tensor de tensión-energía es un campo tensorial de segundo orden que contiene densidades de energía-momento, flujos de energía-momento y tensiones de corte de una distribución de masa-energía. La forma diferencial de conservación de energía-momento en la relatividad general establece que la divergencia covariante del tensor de tensión-energía es cero:$${\displaystyle {T^{\mu }}_{\nu ;\mu }=0.}$$

Esta es una restricción importante sobre la forma que toman las ecuaciones de campo de Einstein en la relatividad general . ^[5]

Sin embargo, la divergencia ordinaria del tensor de tensión-energía no desaparece necesariamente: ^[6]$${\displaystyle \partial _{\mu }T^{\mu \nu }=-\Gamma _{\mu \lambda }^{\mu }T^{\lambda \nu }-\Gamma _{\mu \lambda }^{\nu }T^{\mu \lambda },}$$

El lado derecho desaparece estrictamente solo para una geometría plana.

Como consecuencia, la forma integral de la ecuación de continuidad es difícil de definir y no necesariamente válida para una región dentro de la cual el espacio-tiempo está significativamente curvado (por ejemplo, alrededor de un agujero negro o en todo el universo). ^[7]

Los quarks y los gluones tienen carga de color , que siempre se conserva como la carga eléctrica, y existe una ecuación de continuidad para dichas corrientes de carga de color (las expresiones explícitas para las corrientes se dan en el tensor de intensidad de campo de gluones ).

Hay muchas otras cantidades en física de partículas que a menudo o siempre se conservan: el número bariónico (proporcional al número de quarks menos el número de antiquarks), el número de electrones, el número mu, el número tau , el isospín y otros. ^[8] Cada uno de estos tiene una ecuación de continuidad correspondiente, que posiblemente incluya términos fuente/sumidero.

Una razón por la que las ecuaciones de conservación aparecen con frecuencia en física es el teorema de Noether , que establece que siempre que las leyes de la física tengan una simetría continua , existe una ecuación de continuidad para alguna cantidad física conservada. Los tres ejemplos más famosos son:

• Las leyes de la física son invariantes con respecto a la traslación temporal ; por ejemplo, las leyes de la física de hoy son las mismas que las de ayer. Esta simetría conduce a la ecuación de continuidad para la conservación de la energía .
• Las leyes de la física son invariantes con respecto a la traslación espacial; por ejemplo, un cohete en el espacio exterior no está sujeto a diferentes fuerzas o potenciales si se desplaza en cualquier dirección dada (por ejemplo, x, y, z), lo que conduce a la conservación de los tres componentes del momento: conservación del momento .
• Las leyes de la física son invariables con respecto a la orientación; por ejemplo, si flotas en el espacio exterior, no hay ninguna medida que puedas hacer para saber "en qué dirección estás arriba"; las leyes de la física son las mismas independientemente de cómo estés orientado. Esta simetría conduce a la ecuación de continuidad para la conservación del momento angular .

• Derecho de conservación
• Formulario de conservación
• Sistema disipativo

• Lamb, H. (2006) [1932]. Hidrodinámica (6.ª ed.). Cambridge University Press. ISBN 978-0-521-45868-9.
• Griffiths, DJ (1999). Introducción a la electrodinámica (3.ª ed.). Pearson Education Inc. ISBN 81-7758-293-3.
• Grant, IS; Phillips, WR (2008). Electromagnetismo . Manchester Physics Series (2.ª ed.). ISBN 978-0-471-92712-9.
• Wheeler, JA; Misner, C.; Thorne, KS (1973). Gravitación . WH Freeman & Co. ISBN 0-7167-0344-0.