Vorticidad

Parte de una serie sobre
Mecánica de medios continuos
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ Leyes de difusión de Fick
Leyes Conservaciones Masa Impulso Energía Desigualdades Clausius-Duhem (entropía)
Mecánica de sólidos Deformación Elasticidad lineal Plasticidad Ley de Hooke Estrés Cepa Deformación finita Deformación infinitesimal Compatibilidad Doblado Mecánica de contacto friccional Teoría de la falla del material Mecánica de fracturas
Mecánica de fluidos Fluidos Estática  · Dinámica Principio de Arquímedes  · Principio de Bernoulli Ecuaciones de Navier-Stokes Ecuación de Poiseuille  · Ley de Pascal Viscosidad ( Newtoniano  · no newtoniano ) Flotabilidad  · Mezcla  · Presión Líquidos Adhesión Acción capilar Cromatografía Cohesión (química) Tensión superficial Gases Atmósfera Ley de Boyle Ley de Charles Ley combinada de los gases Ley de Fick Ley de Gay-Lussac Ley de Graham Plasma
Reología Viscoelasticidad Reometría Reómetro Fluidos inteligentes Electrorreológico Magnetoreológico Ferrofluidos
Científicos Bernoulli Niño Cauchy Carlos Euler Mierda Gay-Lussac Graham Gancho Newton Navier No Pascal Estoques Verdadero
en a mi

En mecánica de medios continuos , la vorticidad es un campo pseudovectorial (o vector axial) que describe el movimiento giratorio local de un medio continuo cerca de algún punto (la tendencia de algo a rotar ^[1] ), como lo vería un observador ubicado en ese punto y viajando junto con el flujo . Es una cantidad importante en la teoría dinámica de fluidos y proporciona un marco conveniente para comprender una variedad de fenómenos de flujo complejos, como la formación y el movimiento de anillos de vórtices . ^{[2] [3]}

Matemáticamente, la vorticidad es el rizo de la velocidad del flujo : ^{[4] [3]}${\displaystyle {\boldsymbol {\omega }}}$ ${\displaystyle \mathbf {v}}$

${\displaystyle {\boldsymbol {\omega }}\equiv \nabla \times \mathbf {v} \,,}$

donde es el operador nabla . Conceptualmente, podría determinarse marcando partes de un continuo en una pequeña vecindad del punto en cuestión, y observando sus desplazamientos relativos a medida que se mueven a lo largo del flujo. La vorticidad sería el doble del vector de velocidad angular media de esas partículas con respecto a su centro de masa , orientado de acuerdo con la regla de la mano derecha . Por su propia definición, el vector de vorticidad es un campo solenoidal ya que${\displaystyle \nabla}$${\displaystyle {\boldsymbol {\omega }}}$ ${\displaystyle {\boldsymbol {\omega }}}$${\displaystyle \nabla \cdot {\boldsymbol {\omega }}=0.}$

En un flujo bidimensional , siempre es perpendicular al plano del flujo y, por lo tanto, puede considerarse un campo escalar .${\displaystyle {\boldsymbol {\omega }}}$

Matemáticamente, la vorticidad de un flujo tridimensional es un campo pseudovectorial, normalmente denotado por , definido como el rizo del campo de velocidad que describe el movimiento continuo. En coordenadas cartesianas :${\displaystyle {\boldsymbol {\omega }}}$${\displaystyle \mathbf {v}}$

${\displaystyle {\begin{aligned}{\boldsymbol {\omega }}=\nabla \times \mathbf {v} =\left({\dfrac {\partial v_{z}}{\partial y}}-{\dfrac {\partial v_{y}}{\partial z}},{\dfrac {\partial v_{x}}{\partial z}}-{\dfrac {\partial v_{z}}{\partial x}},{\dfrac {\partial v_{y}}{\partial x}}-{\dfrac {\partial v_{x}}{\partial y}}\right)\,.\end{aligned}}}$

En palabras, la vorticidad nos dice cómo cambia el vector de velocidad cuando uno se mueve una distancia infinitesimal en una dirección perpendicular a ella.

En un flujo bidimensional donde la velocidad es independiente de la coordenada y no tiene componente, el vector de vorticidad siempre es paralelo al eje y, por lo tanto, puede expresarse como un campo escalar multiplicado por un vector unitario constante :${\displaystyle z}$${\displaystyle z}$${\displaystyle z}$${\displaystyle {\hat {z}}}$

${\displaystyle {\begin{aligned}{\boldsymbol {\omega }}=\nabla \times \mathbf {v} =\left({\frac {\partial v_{y}}{\partial x}}-{\frac {\partial v_{x}}{\partial y}}\right)\mathbf {e} _{z}\,.\end{aligned}}}$

La vorticidad también está relacionada con la circulación del flujo (integral lineal de la velocidad) a lo largo de un camino cerrado por el teorema de Stokes (clásico) . Es decir, para cualquier elemento de superficie infinitesimal C con dirección normal y área , la circulación a lo largo del perímetro de es el producto escalar donde es la vorticidad en el centro de . ^[5] ${\displaystyle \mathbf {n} }$${\displaystyle dA}$${\displaystyle d\Gamma }$${\displaystyle C}$ ${\displaystyle {\boldsymbol {\omega }}\cdot (\mathbf {n} \,dA)}$${\displaystyle {\boldsymbol {\omega }}}$${\displaystyle C}$

Como la vorticidad es un vector axial, se puede asociar con un tensor antisimétrico de segundo orden (el llamado tensor de vorticidad o de rotación), que se dice que es el dual de . La relación entre las dos cantidades, en notación de índice, se da por${\displaystyle {\boldsymbol {\Omega }}}$${\displaystyle {\boldsymbol {\omega }}}$

${\displaystyle \Omega _{ij}=\varepsilon _{ijk}\omega _{k},\qquad \omega _{i}={\frac {1}{2}}\varepsilon _{ijk}\Omega _{jk}}$

donde es el tensor tridimensional de Levi-Civita . El tensor de vorticidad es simplemente la parte antisimétrica del tensor , es decir,${\displaystyle \varepsilon _{ijk}}$${\displaystyle \nabla \mathbf {v} }$

${\displaystyle {\boldsymbol {\Omega }}={\frac {1}{2}}\left[\nabla \mathbf {v} -(\nabla \mathbf {v} )^{T}\right]\quad {\text{or}}\quad \Omega _{ij}={\frac {1}{2}}\left({\frac {\partial v_{i}}{\partial x_{j}}}-{\frac {\partial v_{j}}{\partial x_{i}}}\right).}$

En una masa de continuo que gira como un cuerpo rígido, la vorticidad es el doble del vector de velocidad angular de esa rotación. Este es el caso, por ejemplo, en el núcleo central de un vórtice de Rankine . ^[6]

La vorticidad puede ser distinta de cero incluso cuando todas las partículas fluyen a lo largo de trayectorias rectas y paralelas , si hay cizallamiento (es decir, si la velocidad del flujo varía a través de las líneas de corriente ). Por ejemplo, en el flujo laminar dentro de una tubería con sección transversal constante , todas las partículas viajan paralelas al eje de la tubería; pero más rápido cerca de ese eje, y prácticamente estacionarias junto a las paredes. La vorticidad será cero en el eje, y máxima cerca de las paredes, donde el cizallamiento es mayor.

Por el contrario, un flujo puede tener vorticidad cero aunque sus partículas viajen a lo largo de trayectorias curvas. Un ejemplo es el vórtice irrotacional ideal , donde la mayoría de las partículas giran alrededor de un eje recto, con una velocidad inversamente proporcional a sus distancias a ese eje. Una pequeña porción de continuo que no se extiende a ambos lados del eje rotará en un sentido pero se cortará en el sentido opuesto, de tal manera que su velocidad angular media alrededor de su centro de masas sea cero.

Flujos de ejemplo:
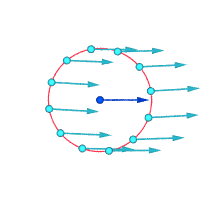
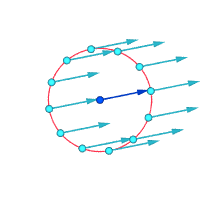
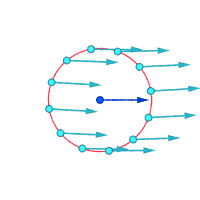
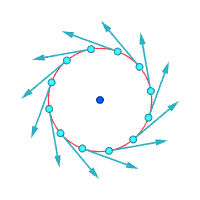
Vórtice de tipo cuerpo rígido v ∝ r	Flujo paralelo con cizallamiento	Vórtice irrotacional v ∝ ⁠1/a⁠
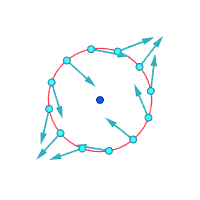
donde v es la velocidad del flujo, r es la distancia al centro del vórtice y ∝ indica proporcionalidad . Velocidades absolutas alrededor del punto resaltado:
Velocidades relativas (ampliadas) alrededor del punto resaltado
Vorticidad ≠ 0	Vorticidad ≠ 0	Vorticidad = 0

Otra forma de visualizar la vorticidad es imaginar que, instantáneamente, una pequeña parte del continuo se vuelve sólida y el resto del flujo desaparece. Si esa pequeña nueva partícula sólida está rotando, en lugar de simplemente moverse con el flujo, entonces hay vorticidad en el flujo. En la figura siguiente, la subfigura de la izquierda demuestra que no hay vorticidad y la subfigura de la derecha demuestra que sí la hay.

La evolución del campo de vorticidad en el tiempo se describe mediante la ecuación de vorticidad , que puede derivarse de las ecuaciones de Navier-Stokes . ^[7]

En muchos flujos reales en los que la viscosidad puede despreciarse (más precisamente, en flujos con un alto número de Reynolds ), el campo de vorticidad puede modelarse mediante una colección de vórtices discretos, siendo la vorticidad despreciable en todas partes excepto en pequeñas regiones del espacio que rodean los ejes de los vórtices. Esto es cierto en el caso del flujo potencial bidimensional (es decir, flujo bidimensional de viscosidad cero), en cuyo caso el campo de flujo puede modelarse como un campo de valor complejo en el plano complejo .

La vorticidad es útil para comprender cómo se pueden alterar las soluciones de flujo potencial ideales para modelar flujos reales. En general, la presencia de viscosidad provoca una difusión de la vorticidad desde los núcleos de los vórtices hacia el campo de flujo general; este flujo se explica por un término de difusión en la ecuación de transporte de vorticidad. ^[8]

Una línea de vórtice o línea de vorticidad es una línea que es tangente en todas partes al vector de vorticidad local. Las líneas de vórtice se definen mediante la relación ^[9]

${\displaystyle {\frac {dx}{\omega _{x}}}={\frac {dy}{\omega _{y}}}={\frac {dz}{\omega _{z}}}\,,}$

donde es el vector de vorticidad en coordenadas cartesianas .${\displaystyle {\boldsymbol {\omega }}=(\omega _{x},\omega _{y},\omega _{z})}$

Un tubo de vórtice es la superficie en el continuo formada por todas las líneas de vórtice que pasan a través de una curva cerrada dada (reducible) en el continuo. La "fuerza" de un tubo de vórtice (también llamado flujo de vórtice ) ^[10] es la integral de la vorticidad a través de una sección transversal del tubo, y es la misma en todas partes a lo largo del tubo (porque la vorticidad tiene divergencia cero). Es una consecuencia de los teoremas de Helmholtz (o equivalentemente, del teorema de circulación de Kelvin ) que en un fluido no viscoso la "fuerza" del tubo de vórtice también es constante con el tiempo. Los efectos viscosos introducen pérdidas por fricción y dependencia del tiempo. ^[11]

En un flujo tridimensional, la vorticidad (medida por la integral de volumen del cuadrado de su magnitud) se puede intensificar cuando se extiende una línea de vórtice, un fenómeno conocido como estiramiento de vórtice . ^[12] Este fenómeno ocurre en la formación de un vórtice de bañera en el agua que sale y en la acumulación de un tornado por corrientes de aire ascendentes.

El ingeniero hidráulico ruso A. Ya. Milovich (1874-1958) inventó un medidor de vorticidad de paletas rotativas. En 1913, propuso un corcho con cuatro paletas adheridas como dispositivo que mostraba cualitativamente la magnitud de la proyección vertical de la vorticidad y mostró una fotografía en movimiento del movimiento del flotador sobre la superficie del agua en un modelo de un recodo de un río. ^[13]

^{Los medidores de vorticidad de paletas rotativas se muestran comúnmente en películas educativas sobre mecánica de medios continuos (ejemplos famosos incluyen "Vorticity" [14]} del NCFMF y "Fundamental Principles of Flow" del Iowa Institute of Hydraulic Research ^[15] ).

En aerodinámica , la distribución de sustentación sobre un ala finita puede aproximarse suponiendo que cada segmento del ala a lo largo de su envergadura tiene un vórtice de cola semiinfinito detrás de él. Entonces es posible calcular la fuerza de los vórtices utilizando el criterio de que no haya flujo inducido a través de la superficie del ala. Este procedimiento se denomina método del panel de vórtices de dinámica de fluidos computacional . Luego se suman las fuerzas de los vórtices para encontrar la circulación total aproximada alrededor del ala. Según el teorema de Kutta-Joukowski , la sustentación por unidad de envergadura es el producto de la circulación, la velocidad del aire y la densidad del aire.

La vorticidad relativa es la vorticidad relativa a la Tierra inducida por el campo de velocidad del aire. Este campo de velocidad del aire se modela a menudo como un flujo bidimensional paralelo al suelo, de modo que el vector de vorticidad relativa es generalmente una cantidad de rotación escalar perpendicular al suelo. La vorticidad es positiva cuando, mirando hacia la superficie de la Tierra, el viento gira en sentido contrario a las agujas del reloj. En el hemisferio norte, la vorticidad positiva se denomina rotación ciclónica y la vorticidad negativa, rotación anticiclónica ; la nomenclatura se invierte en el hemisferio sur.

La vorticidad absoluta se calcula a partir de la velocidad del aire relativa a un marco inercial y, por lo tanto, incluye un término debido a la rotación de la Tierra, el parámetro de Coriolis .

La vorticidad potencial es la vorticidad absoluta dividida por el espaciamiento vertical entre niveles de temperatura (o entropía ) (potencial) constante . La vorticidad absoluta de una masa de aire cambiará si la masa de aire se estira (o se comprime) en la dirección vertical, pero la vorticidad potencial se conserva en un flujo adiabático . Como el flujo adiabático predomina en la atmósfera, la vorticidad potencial es útil como un trazador aproximado de las masas de aire en la atmósfera en la escala de tiempo de unos pocos días, particularmente cuando se observa en niveles de entropía constante.

La ecuación de vorticidad barotrópica es la forma más sencilla de predecir el movimiento de las ondas de Rossby (es decir, los valles y crestas de una altura geopotencial de 500  hPa ) durante un período de tiempo limitado (unos días). En la década de 1950, los primeros programas de predicción numérica del tiempo que funcionaron con éxito utilizaron esa ecuación.

En los modelos numéricos de predicción meteorológica modernos y los modelos de circulación general (GCM), la vorticidad puede ser una de las variables predichas, en cuyo caso la ecuación dependiente del tiempo correspondiente es una ecuación de pronóstico .

Relacionado con el concepto de vorticidad está la helicidad , definida como${\displaystyle H(t)}$

${\displaystyle H(t)=\int _{V}\mathbf {v} \cdot {\boldsymbol {\omega }}\,dV}$

donde la integral es sobre un volumen dado . En la ciencia atmosférica, la helicidad del movimiento del aire es importante para pronosticar supercélulas y el potencial de actividad tornádica . ^[16]${\displaystyle V}$

• Ecuación de vorticidad barotrópica
• La paradoja de D'Alembert
• Enstrofia
• Palinstrofia
• Potencial de velocidad
• Vórtice
• Tubo de vórtice
• Estiramiento de vórtice
• Vórtice de herradura
• Vórtices en las puntas de las alas

• Ley de Biot-Savart
• Circulación
• Ecuaciones de vorticidad
• Teorema de Kutta-Joukowski

• Ecuación de pronóstico
• Carl Gustav Rossby
• Hans Ertel

• Acheson, DJ (1990). Dinámica de fluidos elemental . Oxford University Press. ISBN 0-19-859679-0.
• Landau, LD; Lifshitz, EM (1987). Mecánica de fluidos (2ª ed.). Elsevier. ISBN 978-0-08-057073-0.
• Pozrikidis, C. (2011). Introducción a la dinámica de fluidos teórica y computacional . Oxford University Press. ISBN 978-0-19-975207-2.
• Guyon, Etienne; Hulin, Jean-Pierre; Pequeño, Luc; Mitescu, Catalin D. (2001). Hidrodinámica física . Prensa de la Universidad de Oxford. ISBN 0-19-851746-7.
• Batchelor, GK (2000) [1967], Introducción a la dinámica de fluidos , Cambridge University Press, ISBN 0-521-66396-2
• Clancy, LJ (1975), Aerodinámica , Pitman Publishing Limited, Londres ISBN 0-273-01120-0 
• " Glosario del tiempo "' The Weather Channel Interactive, Inc.. 2004.
• " Vorticidad ". Editorial Integrada.

• Ohkitani, K., " Elementary Account Of Vortity And Related Equations ". Cambridge University Press. 30 de enero de 2005. ISBN 0-521-81984-9 
• Chorin, Alexandre J. , " Vorticidad y turbulencia ". Applied Mathematical Sciences, vol. 103, Springer-Verlag, 1 de marzo de 1994. ISBN 0-387-94197-5 
• Majda, Andrew J. , Andrea L. Bertozzi, " Vorticidad y flujo incompresible ". Cambridge University Press; 2002. ISBN 0-521-63948-4 
• Tritton, DJ , " Dinámica de fluidos físicos ". Van Nostrand Reinhold, Nueva York. 1977. ISBN 0-19-854493-6 
• Arfken, G., " Métodos matemáticos para físicos ", 3.ª ed. Academic Press, Orlando, Florida, 1985. ISBN 0-12-059820-5 

Wikimedia Commons tiene medios relacionados con Vorticidad .

• Weisstein, Eric W., " Vorticidad ". Scienceworld.wolfram.com.
• Doswell III, Charles A., " Una introducción a la vorticidad para su aplicación en supercélulas y tornados ". Instituto Cooperativo de Estudios Meteorológicos de Mesoescala, Norman, Oklahoma.
• Cramer, MS, " Ecuaciones de Navier-Stokes - Teoremas de transporte de vorticidad: Introducción ". Fundamentos de mecánica de fluidos.
• Parker, Douglas, " ENVI 2210 – Atmosphere and Ocean Dynamics, 9: Vorticidad ". Facultad de Medio Ambiente, Universidad de Leeds. Septiembre de 2001.
• Graham, James R. , " Astronomía 202: Dinámica astrofísica de los gases ". Departamento de Astronomía, UC Berkeley .
  • " La ecuación de vorticidad: fluidos incompresibles y barotrópicos ".
  • " Interpretación de la ecuación de vorticidad ".
  • " Teorema de vorticidad de Kelvin para flujo incompresible o barotrópico ".
• " Spherepack 3.1 Archivado el 22 de junio de 2004 en Wayback Machine . (incluye una colección de programas de vorticidad en FORTRAN)
• " Comunidad compresible de mesoescala (MC2) ^{[ vínculo muerto permanente ]} Predicciones del modelo en tiempo real ". (Análisis de vorticidad potencial)