Círculo

Círculo
Un circulo   circunferencia C   diámetro D   radio R   centro u origen O
Tipo	Sección cónica
Grupo de simetría	O(2)
Área	πR2​
Perímetro	C = 2πR

Un círculo es una figura que consta de todos los puntos de un plano que se encuentran a una distancia dada de un punto dado, el centro . La distancia entre cualquier punto del círculo y el centro se llama radio . La longitud de un segmento de línea que conecta dos puntos del círculo y pasa por el centro se llama diámetro . Un círculo limita una región del plano llamada disco .

El círculo se conoce desde antes del comienzo de la historia escrita. Son comunes los círculos naturales, como la luna llena o una rodaja de fruta redonda. El círculo es la base de la rueda , que, junto con inventos relacionados como los engranajes , hace posible gran parte de la maquinaria moderna. En matemáticas, el estudio del círculo ha ayudado a inspirar el desarrollo de la geometría, la astronomía y el cálculo .

• Anillo : objeto con forma de anillo, región delimitada por dos círculos concéntricos .
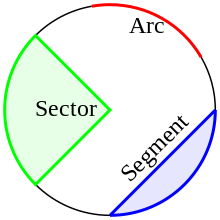
• Arco : cualquier parte conectada de un círculo. Si se especifican dos puntos finales de un arco y un centro, se pueden formar dos arcos que juntos forman un círculo completo.
• Centro : el punto equidistante de todos los puntos del círculo.
• Cuerda : segmento de línea cuyos extremos se encuentran en el círculo, dividiendo así el círculo en dos segmentos.
• Circunferencia : la longitud de un circuito a lo largo del círculo, o la distancia alrededor del círculo.
• Diámetro : segmento de línea cuyos puntos finales se encuentran en el círculo y que pasa por el centro; o la longitud de dicho segmento de línea. Es la distancia más grande entre dos puntos cualesquiera en el círculo. Es un caso especial de cuerda, es decir, la cuerda más larga de un círculo dado, y su longitud es el doble de la longitud de un radio.
• Disco : la región del plano delimitada por un círculo. En el uso matemático estricto, un círculo es solo el límite del disco (o disco), mientras que en el uso cotidiano el término "círculo" también puede referirse a un disco.
• Lente : la región común a (la intersección de) dos discos superpuestos.
• Radio : segmento de línea que une el centro de un círculo con cualquier punto del círculo mismo; o la longitud de dicho segmento, que es la mitad (de la longitud de) un diámetro. Por lo general, el radio se denota y se requiere que sea un número positivo. Un círculo con es un caso degenerado que consiste en un solo punto.${\estilo de visualización r}$${\displaystyle r=0}$
• Sector : región delimitada por dos radios de igual longitud con un centro común y cualquiera de los dos arcos posibles, determinados por este centro y los puntos finales de los radios.
• Segmento : región limitada por una cuerda y uno de los arcos que unen los extremos de la cuerda. La longitud de la cuerda impone un límite inferior al diámetro de los arcos posibles. A veces, el término segmento se utiliza solo para regiones que no contienen el centro del círculo al que pertenece su arco.
• Secante : cuerda prolongada, línea recta coplanar, que interseca un círculo en dos puntos.
• Semicírculo : uno de los dos arcos posibles determinados por los puntos extremos de un diámetro, tomando como centro su punto medio. En el uso común no técnico puede significar el interior de la región bidimensional delimitada por un diámetro y uno de sus arcos, que técnicamente se denomina semidisco. Un semidisco es un caso especial de segmento, es decir, el mayor.
• Tangente : línea recta coplanar que tiene un solo punto en común con un círculo ("toca el círculo en este punto").

Todas las regiones especificadas pueden considerarse abiertas , es decir, que no contienen sus límites, o cerradas , incluidos sus respectivos límites.

La palabra círculo deriva del griego κίρκος/κύκλος ( kirkos/kuklos ), a su vez una metátesis del griego homérico κρίκος ( krikos ), que significa "aro" o "anillo". ^[1] Los orígenes de las palabras circo y circuito están estrechamente relacionados.

Los pueblos prehistóricos hacían círculos de piedra y de madera , y los elementos circulares son comunes en los petroglifos y las pinturas rupestres . ^[2] Los artefactos prehistóricos con forma de disco incluyen el disco celeste de Nebra y los discos de jade llamados Bi .

El papiro egipcio Rhind , que data del año 1700 a. C., ofrece un método para hallar el área de un círculo. El resultado corresponde a ⁠256/81⁠ (3,16049...) como valor aproximado de π . ^[3]

El libro 3 de los Elementos de Euclides trata de las propiedades de los círculos. La definición de círculo que da Euclides es:

Un círculo es una figura plana limitada por una línea curva, y tal que todas las líneas rectas trazadas desde un punto determinado dentro de ella hasta la línea límite son iguales. La línea límite se llama circunferencia y el punto, centro.

—  Euclides , Libro I , Elementos ^{[4] : ​​4}

En la Séptima Carta de Platón hay una definición y explicación detallada del círculo. Platón explica el círculo perfecto y en qué se diferencia de cualquier dibujo, palabra, definición o explicación. La ciencia primitiva , en particular la geometría , la astrología y la astronomía , estaba conectada con lo divino para la mayoría de los eruditos medievales , y muchos creían que había algo intrínsecamente "divino" o "perfecto" que se podía encontrar en los círculos. ^{[5] [6]}

En 1880 d. C., Ferdinand von Lindemann demostró que π es trascendental , demostrando que el problema milenario de la cuadratura del círculo no se puede resolver con regla y compás. ^[7]

Con la llegada del arte abstracto a principios del siglo XX, los objetos geométricos se convirtieron en un tema artístico por derecho propio. Wassily Kandinsky , en particular, utilizó a menudo círculos como elemento de sus composiciones. ^{[8] [9]}

Desde la época de las primeras civilizaciones conocidas (como los asirios y los antiguos egipcios, los del valle del Indo y a lo largo del río Amarillo en China, y las civilizaciones occidentales de la antigua Grecia y Roma durante la Antigüedad clásica), el círculo se ha utilizado directa o indirectamente en el arte visual para transmitir el mensaje del artista y expresar ciertas ideas. Sin embargo, las diferencias en la cosmovisión (creencias y cultura) tuvieron un gran impacto en las percepciones de los artistas. Mientras que algunos enfatizaban el perímetro del círculo para demostrar su manifestación democrática, otros se centraban en su centro para simbolizar el concepto de unidad cósmica. En las doctrinas místicas, el círculo simboliza principalmente la naturaleza infinita y cíclica de la existencia, pero en las tradiciones religiosas representa los cuerpos celestes y los espíritus divinos.

El círculo simboliza muchos conceptos sagrados y espirituales, entre ellos la unidad, el infinito, la totalidad, el universo, la divinidad, el equilibrio, la estabilidad y la perfección, entre otros. Dichos conceptos se han transmitido en culturas de todo el mundo mediante el uso de símbolos, por ejemplo, una brújula, un halo, la vesica piscis y sus derivados (pez, ojo, aureola, mandorla, etc.), el ouroboros, la rueda del Dharma , un arco iris, mandalas, rosetones, etc. ^[10] Los círculos mágicos forman parte de algunas tradiciones del esoterismo occidental .

La razón entre la circunferencia de un círculo y su diámetro es π (pi), una constante irracional aproximadamente igual a 3,141592654. La razón entre la circunferencia de un círculo y su radio es 2 π . ^[a] Por lo tanto, la circunferencia C está relacionada con el radio r y el diámetro d por:$${\displaystyle C=2\pi r=\pi d.}$$

Como lo demostró Arquímedes en su Medida del círculo , el área encerrada por un círculo es igual a la de un triángulo cuya base tiene la longitud de la circunferencia del círculo y cuya altura es igual al radio del círculo, ^[11] lo que da π multiplicado por el radio al cuadrado:$${\displaystyle \mathrm {Área} =\pi r^{2}.}$$

De manera equivalente, se denota el diámetro por d , es decir, aproximadamente el 79% del cuadrado que lo circunscribe (cuyo lado tiene longitud d ).$${\displaystyle \mathrm {Área} ={\frac {\pi d^{2}}{4}}\aproximadamente 0,7854d^{2},}$$

El círculo es la curva plana que encierra el área máxima para una longitud de arco dada. Esto relaciona el círculo con un problema en el cálculo de variaciones, a saber, la desigualdad isoperimétrica .

Si un círculo de radio r está centrado en el vértice de un ángulo , y ese ángulo intercepta un arco del círculo con una longitud de arco de s , entonces la medida en radianes 𝜃 del ángulo es la relación entre la longitud del arco y el radio:$${\displaystyle \theta ={\frac {s}{r}}.}$$

Se dice que el arco circular subtiende el ángulo, conocido como ángulo central , en el centro del círculo. El ángulo subtendido por un círculo completo en su centro es un ángulo completo , que mide 2 π radianes, 360 grados o una vuelta .

Usando radianes, la fórmula para la longitud de arco s de un arco circular de radio r y que subtiende un ángulo central de medida 𝜃 es$${\displaystyle s=\theta r,}$$

y la fórmula para el área A de un sector circular de radio r y con ángulo central de medida 𝜃 es$${\displaystyle A={\frac {1}{2}}\theta r^{2}.}$$

En el caso especial 𝜃 = 2 π , estas fórmulas dan como resultado la circunferencia de un círculo completo y el área de un disco completo, respectivamente.

En un sistema de coordenadas cartesianas x – y , el círculo con coordenadas centrales ( a , b ) y radio r es el conjunto de todos los puntos ( x , y ) tales que$${\displaystyle (xa)^{2}+(yb)^{2}=r^{2}.}$$

Esta ecuación , conocida como ecuación del círculo , se deriva del teorema de Pitágoras aplicado a cualquier punto del círculo: como se muestra en el diagrama adyacente, el radio es la hipotenusa de un triángulo rectángulo cuyos otros lados tienen longitud | x − a | y | y − b |. Si el círculo está centrado en el origen (0, 0), entonces la ecuación se simplifica a$${\displaystyle x^{2}+y^{2}=r^{2}.}$$

La ecuación se puede escribir en forma paramétrica utilizando las funciones trigonométricas seno y coseno como donde t es una variable paramétrica en el rango de 0 a 2 π , interpretada geométricamente como el ángulo que el rayo de ( a ,  b ) a ( x ,  y ) forma con el  eje x positivo.$${\displaystyle {\begin{aligned}x&=a+r\,\cos t,\\y&=b+r\,\sin t,\end{aligned}}}$$

Una parametrización alternativa del círculo es$${\displaystyle {\begin{aligned}x&=a+r{\frac {1-t^{2}}{1+t^{2}}},\\y&=b+r{\frac {2t}{1+t^{2}}}.\end{aligned}}}$$

En esta parametrización, la relación entre t y r se puede interpretar geométricamente como la proyección estereográfica de la línea que pasa por el centro paralela al eje x  (véase Sustitución de la mitad del ángulo tangente ). Sin embargo, esta parametrización funciona solo si se hace que t recorra no solo todos los números reales sino también un punto en el infinito; de lo contrario, se omitiría el punto más a la izquierda del círculo.

La ecuación del círculo determinada por tres puntos que no están en una línea se obtiene mediante una conversión de la forma de 3 puntos de una ecuación circular :${\displaystyle (x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})}$$${\displaystyle {\frac {({\color {green}x}-x_{1})({\color {green}x}-x_{2})+({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {green}x}-x_{2})-({\color {red}y}-y_{2})({\color {green}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}.}$$

En coordenadas homogéneas , cada sección cónica con ecuación de círculo tiene la forma$${\displaystyle x^{2}+y^{2}-2axz-2byz+cz^{2}=0.}$$

Se puede demostrar que una sección cónica es un círculo exactamente cuando contiene (al extenderse al plano proyectivo complejo ) los puntos I (1: i : 0) y J (1: − i : 0). Estos puntos se denominan puntos circulares en el infinito .

En coordenadas polares , la ecuación de un círculo es$${\displaystyle r^{2}-2rr_{0}\cos(\theta -\phi )+r_{0}^{2}=a^{2},}$$

donde a es el radio del círculo, son las coordenadas polares de un punto genérico en el círculo y son las coordenadas polares del centro del círculo (es decir, r ₀ es la distancia desde el origen hasta el centro del círculo y φ es el ángulo en sentido antihorario desde el eje x positivo  hasta la línea que conecta el origen con el centro del círculo). Para un círculo centrado en el origen, es decir, r ₀ = 0 , esto se reduce a r = a . Cuando r ₀ = a , o cuando el origen se encuentra en el círculo, la ecuación se convierte en${\displaystyle (r,\theta )}$${\displaystyle (r_{0},\phi )}$$${\displaystyle r=2a\cos(\theta -\phi ).}$$

En el caso general, la ecuación se puede resolver para r , obteniéndose Sin el signo ±, la ecuación en algunos casos describiría solo medio círculo.$${\displaystyle r=r_{0}\cos(\theta -\phi )\pm {\sqrt {a^{2}-r_{0}^{2}\sin ^{2}(\theta -\phi )}}.}$$

En el plano complejo , un círculo con centro en c y radio r tiene la ecuación$${\displaystyle |z-c|=r.}$$

En forma paramétrica, esto se puede escribir como$${\displaystyle z=re^{it}+c.}$$

La ecuación ligeramente generalizada$${\displaystyle pz{\overline {z}}+gz+{\overline {gz}}=q}$$

Para p , q reales y g complejas, a veces se le llama círculo generalizado . Esto se convierte en la ecuación anterior para un círculo con , ya que . No todos los círculos generalizados son realmente círculos: un círculo generalizado es un círculo (verdadero) o una línea .${\displaystyle p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}}$${\displaystyle |z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}}$

La recta tangente que pasa por un punto P en el círculo es perpendicular al diámetro que pasa por P. Si P = ( x ₁ , y ₁ ) y el círculo tiene centro ( a , b ) y radio r , entonces la recta tangente es perpendicular a la recta que va de ( a , b ) a ( x ₁ , y ₁ ), por lo que tiene la forma ( x ₁ − a ) x + ( y ₁ – b ) y = c . Al evaluar en ( x ₁ , y ₁ ) se determina el valor de c , y el resultado es que la ecuación de la tangente es o$${\displaystyle (x_{1}-a)x+(y_{1}-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{1},}$$$${\displaystyle (x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}.}$$

Si y ₁ ≠ b , entonces la pendiente de esta línea es$${\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}-a}{y_{1}-b}}.}$$

Esto también se puede encontrar utilizando la diferenciación implícita .

Cuando el centro del círculo está en el origen, entonces la ecuación de la línea tangente se convierte en y su pendiente es$${\displaystyle x_{1}x+y_{1}y=r^{2},}$$$${\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}}{y_{1}}}.}$$

• El círculo es la figura con mayor área para una longitud de perímetro dada (ver desigualdad isoperimétrica ).
• El círculo es una figura altamente simétrica: cada línea que pasa por el centro forma una línea de simetría de reflexión y tiene simetría rotacional alrededor del centro para cada ángulo. Su grupo de simetría es el grupo ortogonal O(2, R ). El grupo de rotaciones por sí solo es el grupo del círculo T.
• Todos los círculos son semejantes . ^[12]
  • La circunferencia y el radio de un círculo son proporcionales .
  • El área encerrada y el cuadrado de su radio son proporcionales.
  • Las constantes de proporcionalidad son 2 π y π respectivamente.
• El círculo que tiene su centro en el origen y su radio es 1 se denomina círculo unitario .
  • Considerado como un gran círculo de la esfera unitaria , se convierte en el círculo de Riemann .
• A través de tres puntos cualesquiera, no todos sobre la misma línea, se forma una única circunferencia. En coordenadas cartesianas, es posible dar fórmulas explícitas para las coordenadas del centro de la circunferencia y del radio en función de las coordenadas de los tres puntos dados. Véase circunferencia circunscrita .

• Las cuerdas son equidistantes del centro de un círculo si y sólo si tienen la misma longitud.
• La bisectriz perpendicular de una cuerda pasa por el centro de un círculo; enunciados equivalentes derivados de la unicidad de la bisectriz perpendicular son:
  • Una línea perpendicular desde el centro de un círculo biseca la cuerda.
  • El segmento de línea que pasa por el centro y biseca una cuerda es perpendicular a la cuerda.
• Si un ángulo central y un ángulo inscrito de un círculo están subtendidos por la misma cuerda y en el mismo lado de la cuerda, entonces el ángulo central es el doble del ángulo inscrito.
• Si dos ángulos están inscritos en la misma cuerda y en el mismo lado de la cuerda, entonces son iguales.
• Si dos ángulos están inscritos en la misma cuerda y en lados opuestos de la cuerda, entonces son suplementarios .
  • Para un cuadrilátero cíclico , el ángulo exterior es igual al ángulo interior opuesto.
• Un ángulo inscrito subtendido por un diámetro es un ángulo recto (véase el teorema de Tales ).
• El diámetro es la cuerda más larga del círculo.
  • Entre todos los círculos que tienen en común la cuerda AB, el círculo con radio mínimo es el que tiene diámetro AB.
• Si la intersección de dos cuerdas cualesquiera divide una cuerda en longitudes a y b y divide la otra cuerda en longitudes c y d , entonces ab = cd .
• Si la intersección de dos cuerdas perpendiculares divide una cuerda en longitudes a y b y divide la otra cuerda en longitudes c y d , entonces a ² + b ² + c ² + d ² es igual al cuadrado del diámetro. ^[13]
• La suma de las longitudes al cuadrado de dos cuerdas cualesquiera que se intersecan en ángulos rectos en un punto dado es la misma que la de otras dos cuerdas perpendiculares cualesquiera que se intersecan en el mismo punto y está dada por 8 r ² − 4 p ² , donde r es el radio del círculo y p es la distancia desde el punto central hasta el punto de intersección. ^[14]
• La distancia desde un punto del círculo hasta una cuerda dada multiplicada por el diámetro del círculo es igual al producto de las distancias desde el punto hasta los extremos de la cuerda. ^{[15] : p.71}

• Una línea trazada perpendicular a un radio a través del punto final del radio que se encuentra en el círculo es una tangente al círculo.
• Una línea trazada perpendicular a una tangente que pasa por el punto de contacto con un círculo pasa por el centro del círculo.
• Siempre se pueden dibujar dos tangentes a un círculo desde cualquier punto fuera del círculo, y estas tangentes tienen la misma longitud.
• Si una tangente en A y una tangente en B se intersecan en el punto exterior P , entonces denotando el centro como O , los ángulos ∠ BOA y ∠ BPA son suplementarios.
• Si AD es tangente al círculo en A y si AQ es una cuerda del círculo, entonces ∠ DAQ = ⁠1/2⁠ arco( AQ ) .

• El teorema de la cuerda establece que si dos cuerdas, CD y EB , se intersecan en A , entonces AC × AD = AB × AE .
• Si dos secantes, AE y AD , también cortan al círculo en B y C respectivamente, entonces AC × AD = AB × AE (corolario del teorema de la cuerda).
• Una tangente puede considerarse un caso límite de una secante cuyos extremos son coincidentes. Si una tangente desde un punto externo A corta al círculo en F y una secante desde el punto externo A corta al círculo en C y D respectivamente, entonces AF ² = AC × AD (teorema de tangente-secante).
• El ángulo entre una cuerda y la tangente en uno de sus extremos es igual a la mitad del ángulo subtendido en el centro del círculo, en el lado opuesto de la cuerda (ángulo de la cuerda tangente).
• Si el ángulo subtendido por la cuerda en el centro es 90 ° , entonces ℓ = r √2 , donde ℓ es la longitud de la cuerda y r es el radio del círculo.
• Si se inscriben dos secantes en el círculo como se muestra a la derecha, entonces la medida del ángulo A es igual a la mitad de la diferencia de las medidas de los arcos encerrados ( y ). Es decir, , donde O es el centro del círculo (teorema de la secante-secante).${\displaystyle {\overset {\frown }{DE}}}$${\displaystyle {\overset {\frown }{BC}}}$${\displaystyle 2\angle {CAB}=\angle {DOE}-\angle {BOC}}$

Un ángulo inscrito (los ángulos azul y verde de la figura son ejemplos) es exactamente la mitad del ángulo central correspondiente (rojo). Por lo tanto, todos los ángulos inscritos que subtienden el mismo arco (rosa) son iguales. Los ángulos inscritos en el arco (marrón) son suplementarios. En particular, todo ángulo inscrito que subtiende un diámetro es un ángulo recto (ya que el ángulo central mide 180°).

La sagitta (también conocida como versine ) es un segmento de línea dibujado perpendicularmente a una cuerda, entre el punto medio de esa cuerda y el arco del círculo.

Dada la longitud y de una cuerda y la longitud x de la sagitta, se puede utilizar el teorema de Pitágoras para calcular el radio del único círculo que encajará alrededor de las dos líneas:$${\displaystyle r={\frac {y^{2}}{8x}}+{\frac {x}{2}}.}$$

Otra prueba de este resultado, que se basa únicamente en dos propiedades de las cuerdas dadas anteriormente, es la siguiente. Dada una cuerda de longitud y y con una sagitta de longitud x , como la sagitta interseca el punto medio de la cuerda, sabemos que es una parte de un diámetro del círculo. Como el diámetro es el doble del radio, la parte "faltante" del diámetro tiene una longitud de ( 2 r − x ). Utilizando el hecho de que una parte de una cuerda por la otra parte es igual al mismo producto tomado a lo largo de una cuerda que interseca la primera cuerda, encontramos que ( 2 r − x ) x = ( y / 2) ² . Despejando r , encontramos el resultado requerido.

Hay muchas construcciones con compás y regla que dan como resultado círculos.

La construcción más sencilla y básica es la que se realiza teniendo en cuenta el centro del círculo y un punto del mismo. Se coloca la pata fija del compás en el punto central, la pata móvil en el punto del círculo y se gira el compás.

• Construya el punto medio M del diámetro.
• Construye el círculo con centro M que pasa por uno de los extremos del diámetro (también pasará por el otro extremo).

• Nombra los puntos P , Q y R.
• Construye la bisectriz perpendicular del segmento PQ .
• Construye la bisectriz perpendicular del segmento PR .
• Etiqueta el punto de intersección de estas dos bisectrices perpendiculares como M. (Se encuentran porque los puntos no son colineales ).
• Construye el círculo con centro M que pase por uno de los puntos P , Q o R (también pasará por los otros dos puntos).

Apolonio de Perge demostró que un círculo también puede definirse como el conjunto de puntos en un plano que tienen una relación constante (distinta de 1) de distancias a dos focos fijos, A y B. ^{[16] [17]} (El conjunto de puntos donde las distancias son iguales es la bisectriz perpendicular del segmento AB , una línea). A veces se dice que ese círculo se dibuja alrededor de dos puntos.

La prueba consta de dos partes. En primer lugar, hay que demostrar que, dados dos focos A y B y una razón de distancias, cualquier punto P que satisfaga la razón de distancias debe caer en un círculo determinado. Sea C otro punto, que también satisface la razón y se encuentra en el segmento AB . Por el teorema de la bisectriz del ángulo, el segmento de línea PC biseca el ángulo interior APB , ya que los segmentos son similares:$${\displaystyle {\frac {AP}{BP}}={\frac {AC}{BC}}.}$$

Análogamente, un segmento PD que pasa por algún punto D en la prolongación de AB biseca el ángulo exterior correspondiente BPQ, donde Q está en la prolongación de AP . Como los ángulos interior y exterior suman 180 grados, el ángulo CPD es exactamente 90 grados; es decir, un ángulo recto. El conjunto de puntos P tales que el ángulo CPD es un ángulo recto forma un círculo, del cual CD es un diámetro.

En segundo lugar, véase ^{[18] : 15} para una prueba de que cada punto del círculo indicado satisface la relación dada.

Una propiedad estrechamente relacionada de los círculos involucra la geometría de la razón cruzada de los puntos en el plano complejo. Si A , B y C son como se indica arriba, entonces el círculo de Apolonio para estos tres puntos es el conjunto de puntos P para los cuales el valor absoluto de la razón cruzada es igual a uno:$${\displaystyle {\bigl |}[A,B;C,P]{\bigr |}=1.}$$

Dicho de otra manera, P es un punto en el círculo de Apolonio si y sólo si la razón cruzada [ A , B ; C , P ] está en el círculo unitario en el plano complejo.

Si C es el punto medio del segmento AB , entonces el conjunto de puntos P que satisfacen la condición de Apolonio no es un círculo, sino una línea.$${\displaystyle {\frac {|AP|}{|BP|}}={\frac {|AC|}{|BC|}}}$$

Por lo tanto, si A , B y C son puntos distintos en el plano, entonces el lugar geométrico de los puntos P que satisfacen la ecuación anterior se denomina "círculo generalizado". Puede ser un círculo verdadero o una línea. En este sentido, una línea es un círculo generalizado de radio infinito.

En cada triángulo se puede inscribir un círculo único, llamado círculo inscrito , tal que sea tangente a cada uno de los tres lados del triángulo. ^[19]

Alrededor de cada triángulo se puede circunscribir un círculo único, llamado circunferencia circunscrita, de manera que pase por cada uno de los tres vértices del triángulo . ^[20]

Un polígono tangencial , como un cuadrilátero tangencial , es cualquier polígono convexo dentro del cual se puede inscribir un círculo que es tangente a cada lado del polígono. ^[21] Todo polígono regular y todo triángulo es un polígono tangencial.

Un polígono cíclico es cualquier polígono convexo alrededor del cual se puede circunscribir un círculo que pase por cada vértice. Un ejemplo bien estudiado es el cuadrilátero cíclico. Todo polígono regular y todo triángulo es un polígono cíclico. Un polígono que es a la vez cíclico y tangencial se llama polígono bicéntrico .

Una hipocicloide es una curva que se inscribe en un círculo dado trazando un punto fijo en un círculo más pequeño que rueda dentro y tangente al círculo dado.

El círculo puede considerarse como un caso límite de varias otras figuras:

• La serie de polígonos regulares de n lados tiene como límite el círculo cuando n tiende al infinito. Este hecho fue aplicado por Arquímedes para aproximar π .
• Un óvalo cartesiano es un conjunto de puntos tal que la suma ponderada de las distancias desde cualquiera de sus puntos a dos puntos fijos (focos) es una constante. Una elipse es el caso en el que los pesos son iguales. Un círculo es una elipse con una excentricidad de cero, lo que significa que los dos focos coinciden entre sí como el centro del círculo. Un círculo es también un caso especial diferente de un óvalo cartesiano en el que uno de los pesos es cero.
• Una superelipse tiene una ecuación de la forma para a , b y n positivos . Un supercírculo tiene b = a . Un círculo es el caso especial de un supercírculo en el que n = 2 .${\displaystyle \left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1}$
• Un óvalo de Cassini es un conjunto de puntos tal que el producto de las distancias desde cualquiera de sus puntos a dos puntos fijos es una constante. Cuando los dos puntos fijos coinciden, se obtiene un círculo.
• Una curva de ancho constante es una figura cuyo ancho, definido como la distancia perpendicular entre dos líneas paralelas distintas que intersecan cada una su límite en un único punto, es el mismo independientemente de la dirección de esas dos líneas paralelas. El círculo es el ejemplo más simple de este tipo de figura.

Considérese un conjunto finito de puntos en el plano. El lugar geométrico de los puntos tales que la suma de los cuadrados de las distancias a los puntos dados es constante es un círculo, cuyo centro está en el baricentro de los puntos dados. ^[22] Se obtiene una generalización para potencias mayores de distancias si se toman como puntos los vértices del polígono regular . ^[23] El lugar geométrico de los puntos tales que la suma de la -ésima potencia de las distancias a los vértices de un polígono regular dado con radio circunscrito es constante es un círculo, si cuyo centro es el baricentro del .${\displaystyle n}$${\displaystyle n}$${\displaystyle P_{n}}$${\displaystyle 2m}$${\displaystyle d_{i}}$${\displaystyle R}$$${\displaystyle \sum _{i=1}^{n}d_{i}^{2m}>nR^{2m},\quad {\text{ where }}~m=1,2,\dots ,n-1;}$$${\displaystyle P_{n}}$

En el caso del triángulo equilátero , los lugares geométricos de las sumas constantes de las potencias segunda y cuarta son círculos, mientras que para el cuadrado, los lugares geométricos son círculos para las sumas constantes de las potencias segunda, cuarta y sexta. Para el pentágono regular, se sumará la suma constante de las potencias octavas de las distancias, y así sucesivamente.

La cuadratura del círculo es el problema, propuesto por los geómetras antiguos , de construir un cuadrado con la misma área que un círculo dado utilizando sólo un número finito de pasos con compás y regla .

En 1882 se demostró que la tarea era imposible, como consecuencia del teorema de Lindemann-Weierstrass , que demuestra que pi ( π ) es un número trascendental , en lugar de un número irracional algebraico ; es decir, no es la raíz de ningún polinomio con coeficientes racionales . A pesar de la imposibilidad, este tema sigue siendo de interés para los entusiastas de las pseudomatemáticas .

Al definir un círculo como el conjunto de puntos con una distancia fija desde un punto, se pueden considerar diferentes formas como círculos bajo diferentes definiciones de distancia. En la p -norma , la distancia está determinada por En la geometría euclidiana, p = 2, lo que da la familiar$${\displaystyle \left\|x\right\|_{p}=\left(\left|x_{1}\right|^{p}+\left|x_{2}\right|^{p}+\dotsb +\left|x_{n}\right|^{p}\right)^{1/p}.}$$$${\displaystyle \left\|x\right\|_{2}={\sqrt {\left|x_{1}\right|^{2}+\left|x_{2}\right|^{2}+\dotsb +\left|x_{n}\right|^{2}}}.}$$

En la geometría del taxi , p = 1. Los círculos de taxi son cuadrados con lados orientados en un ángulo de 45° con respecto a los ejes de coordenadas. Si bien cada lado tendría una longitud utilizando una métrica euclidiana , donde r es el radio del círculo, su longitud en la geometría del taxi es 2 r . Por lo tanto, la circunferencia de un círculo es 8 r . Por lo tanto, el valor de un análogo geométrico de es 4 en esta geometría. La fórmula para el círculo unitario en la geometría del taxi está en coordenadas cartesianas y en coordenadas polares.${\displaystyle {\sqrt {2}}r}$${\displaystyle \pi }$${\displaystyle |x|+|y|=1}$$${\displaystyle r={\frac {1}{\left|\sin \theta \right|+\left|\cos \theta \right|}}}$$

Un círculo de radio 1 (usando esta distancia) es el vecindario de von Neumann de su centro.

Un círculo de radio r para la distancia de Chebyshev ( métrica L _∞ ) en un plano también es un cuadrado con una longitud de lado 2 r paralelo a los ejes de coordenadas, por lo que la distancia de Chebyshev plana puede considerarse equivalente por rotación y escala a la distancia de taxi plana. Sin embargo, esta equivalencia entre las métricas L ₁ y L _∞ no se generaliza a dimensiones superiores.

El círculo es la hiperesfera unidimensional (la 1-esfera).

En topología , un círculo no se limita al concepto geométrico, sino a todos sus homeomorfismos . Dos círculos topológicos son equivalentes si uno puede transformarse en el otro mediante una deformación de R ³ sobre sí mismo (conocida como isotopía ambiental ). ^[24]

• Esfera afín
• Apeirogon
• Ajuste de círculo
• Distancia
• Problema del círculo de Gauss
• Inversión en un círculo
• Intersección de línea y círculo
• Lista de temas del círculo
• Esfera
• Tres puntos determinan un círculo.
• Traducción de ejes

• Pedoe, Dan (1988). Geometría: un curso completo . Dover. ISBN 9780486658124.

Wikimedia Commons tiene medios relacionados con:
Círculos (categoría)

Wikiquote tiene citas relacionadas con Círculos .

Wikisource tiene el texto del artículo de la Encyclopædia Britannica de 1911 " Círculo ".

• "Círculo". Enciclopedia de Matemáticas . EMS Press . 2001 [1994].
• Círculo en PlanetMath .
• Weisstein, Eric W. "Círculo". MathWorld .
• "Applets interactivos de Java". para las propiedades y construcciones elementales que involucran círculos
• "Ecuación de forma estándar interactiva del círculo". Haga clic y arrastre puntos para ver la ecuación de forma estándar en acción
• "Masticando círculos". Cortar el nudo .