Línea secante

En geometría , una secante es una línea que interseca una curva en un mínimo de dos puntos distintos . ^[1] La palabra secante proviene del latín secare , que significa cortar . ^[2] En el caso de un círculo , una secante interseca el círculo exactamente en dos puntos. Una cuerda es el segmento de línea determinado por los dos puntos, es decir, el intervalo sobre la secante cuyos extremos son los dos puntos. ^[3]

Una línea recta puede intersecar un círculo en cero, uno o dos puntos. Una línea con intersecciones en dos puntos se llama línea secante , en un punto línea tangente y en ningún punto línea exterior . Una cuerda es el segmento de línea que une dos puntos distintos de un círculo. Por lo tanto, una cuerda está contenida en una única línea secante y cada línea secante determina una única cuerda.

En los tratamientos modernos rigurosos de la geometría plana , generalmente se prueban resultados que parecen obvios y que fueron asumidos (sin enunciación) por Euclides en su tratamiento .

Por ejemplo, Teorema (Continuidad Circular Elemental) : ^[4] Si es un círculo y una línea que contiene un punto A que está dentro y un punto B que está fuera de entonces es una línea secante para .${\displaystyle {\mathcal {C}}}$${\displaystyle \ell}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle \ell}$${\displaystyle {\mathcal {C}}}$

En algunas situaciones, expresar los resultados en términos de líneas secantes en lugar de cuerdas puede ayudar a unificar las afirmaciones. Como ejemplo de esto, considere el resultado: ^[5]

Si dos líneas secantes contienen las cuerdas AB y CD en un círculo y se intersecan en un punto P que no está en el círculo, entonces las longitudes de los segmentos de línea satisfacen AP ⋅ PB = CP ⋅ PD .

Si el punto P se encuentra dentro del círculo, se trata de Euclides III.35, pero si el punto se encuentra fuera del círculo, el resultado no está incluido en los Elementos. Sin embargo, Robert Simson, siguiendo a Christopher Clavius , demostró este resultado, a veces llamado teorema de las secantes intersecantes , en sus comentarios sobre Euclides. ^[6]

En el caso de curvas más complicadas que los círculos simples, existe la posibilidad de que una línea intersecte a una curva en más de dos puntos distintos. Algunos autores definen una línea secante de una curva como una línea que interseca la curva en dos puntos distintos. Esta definición deja abierta la posibilidad de que la línea pueda tener otros puntos de intersección con la curva. Cuando se formula de esta manera, las definiciones de una línea secante para círculos y curvas son idénticas y la posibilidad de puntos de intersección adicionales simplemente no se da para un círculo.

Las secantes se pueden utilizar para aproximar la línea tangente a una curva , en algún punto P , si existe. Defina una secante a una curva mediante dos puntos , P y Q , con P fijo y Q variable. A medida que Q se acerca a P a lo largo de la curva, si la pendiente de la secante se acerca a un valor límite , entonces ese límite define la pendiente de la línea tangente en P. ^[1] Las líneas secantes PQ son las aproximaciones a la línea tangente . En cálculo, esta idea es la definición geométrica de la derivada .

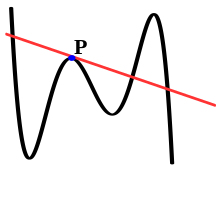
Una línea tangente a una curva en un punto P puede ser una línea secante a esa curva si interseca la curva en al menos un punto distinto de P. Otra forma de ver esto es darse cuenta de que ser una línea tangente en un punto P es una propiedad local , que depende solo de la curva en la vecindad inmediata de P , mientras que ser una línea secante es una propiedad global ya que se necesita examinar todo el dominio de la función que produce la curva.

El concepto de línea secante se puede aplicar en un contexto más general que el espacio euclidiano. Sea K un conjunto finito de k puntos en algún contexto geométrico. Una línea se llamará n -secante de K si contiene exactamente n puntos de K. ^[7] Por ejemplo, si K es un conjunto de 50 puntos dispuestos en un círculo en el plano euclidiano, una línea que une dos de ellos sería una 2-secante (o bisecante ) y una línea que pasa solo por una de ellas sería una 1-secante (o unisecante ). Una unisecante en este ejemplo no necesita ser una línea tangente al círculo.

Esta terminología se utiliza a menudo en geometría de incidencia y geometría discreta . Por ejemplo, el teorema de Sylvester-Gallai de geometría de incidencia establece que si n puntos de geometría euclidiana no son colineales , entonces debe existir una 2-secante de ellos. Y el problema original de plantación de huertos de geometría discreta pide un límite en el número de 3-secantes de un conjunto finito de puntos.

La finitud del conjunto de puntos no es esencial en esta definición, siempre que cada línea pueda intersecar el conjunto sólo en un número finito de puntos.

• Curva elíptica , una curva para la cual cada secante tiene un tercer punto de intersección, a partir del cual se puede definir la mayor parte de una ley de grupo.
• Teorema del valor medio , que establece que cada secante de la gráfica de una función suave tiene una línea tangente paralela
• Cuadrisecante , una línea que interseca cuatro puntos de una curva (normalmente una curva espacial)
• Plano secante , el equivalente tridimensional de una línea secante
• Variedad secante , la unión de líneas secantes y líneas tangentes a una variedad proyectiva dada

• Weisstein, Eric W. "Recta secante". MathWorld .