G2 (matemáticas)

Estructura algebraica → Teoría de grupos Teoría de grupos
Nociones básicas Subgrupo Subgrupo normal Acción grupal Grupo de cocientes Producto (semi) directo Suma directa Producto gratuito Producto de corona Homomorfismos de grupo núcleo imagen simple finito infinito continuo multiplicativo aditivo cíclico abeliano diedro nilpotente soluble Glosario de teoría de grupos Lista de temas de teoría de grupos
Grupos finitos Grupo cíclico Z n Grupo simétrico S n Grupo alterno A n Grupo diedro D n Grupo de cuaterniones Q Teorema de Cauchy Teorema de Lagrange Teoremas de Sylow Teorema de Hall p -grupo Grupo abeliano elemental Grupo Frobenius Multiplicador de Schur Clasificación de grupos finitos simples cíclico alterno Tipo de mentira esporádico
Grupos discretos Celosías Números enteros (${\displaystyle \mathbb {Z}}$) Grupo libre Grupos modulares LPS(2,${\displaystyle \mathbb {Z}}$) SL(2,${\displaystyle \mathbb {Z}}$) Grupo aritmético Enrejado Grupo hiperbólico
Grupos topológicos y de Lie Solenoide Círculo GL lineal general ( n ) SL lineal especial ( n ) O( n ) ortogonal E( n ) euclidiana SO( n ) ortogonal especial Unitario U( n ) SU unitario especial ( n ) Sp( n ) simpléctico G2 F4​ E6​ E7​ E8​ Lorentz Poincaré Conforme Difeomorfismo Bucle Grupo de Lie de dimensión infinita O(∞) SU(∞) Sp(∞)
Grupos algebraicos Grupo algebraico lineal Grupo reductivo Variedad abeliana Curva elíptica
en a mi

Lie groups and Lie algebras
Classical groups General linear GL(n) Special linear SL(n) Orthogonal O(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n)
Simple Lie groups Classical An Bn Cn Dn Exceptional G2 F4 E6 E7 E8
Other Lie groups Circle Lorentz Poincaré Conformal group Diffeomorphism Loop Euclidean
Lie algebras Lie group–Lie algebra correspondence Exponential map Adjoint representation Killing form Index Simple Lie algebra Loop algebra Affine Lie algebra
Semisimple Lie algebra Dynkin diagrams Cartan subalgebra Root system Weyl group Real form Complexification Split Lie algebra Compact Lie algebra
Representation theory Lie group representation Lie algebra representation Representation theory of semisimple Lie algebras Representations of classical Lie groups Theorem of the highest weight Borel–Weil–Bott theorem
Lie groups in physics Particle physics and representation theory Lorentz group representations Poincaré group representations Galilean group representations
Scientists Sophus Lie Henri Poincaré Wilhelm Killing Élie Cartan Hermann Weyl Claude Chevalley Harish-Chandra Armand Borel
Glossary Table of Lie groups
v t e

En matemáticas , G ₂ son tres grupos de Lie simples (una forma compleja, una forma real compacta y una forma real dividida), sus álgebras de Lie así como algunos grupos algebraicos . Son los más pequeños de los cinco grupos de Lie simples excepcionales . G ₂ tiene rango 2 y dimensión 14. Tiene dos representaciones fundamentales , con dimensión 7 y 14.${\displaystyle {\mathfrak {g}}_{2},}$

La forma compacta de G ₂ puede describirse como el grupo de automorfismos del álgebra de octoniones o, equivalentemente, como el subgrupo de SO(7) que preserva cualquier vector particular elegido en su representación de espín real de 8 dimensiones (una representación de espín ).

El álgebra de Lie , siendo la más pequeña de las álgebras de Lie simples excepcionales, fue la primera de ellas en ser descubierta en el intento de clasificar las álgebras de Lie simples. El 23 de mayo de 1887, Wilhelm Killing escribió una carta a Friedrich Engel diciendo que había encontrado un álgebra de Lie simple de 14 dimensiones, que ahora llamamos . ^[1]${\displaystyle {\mathfrak {g}}_{2}}$${\displaystyle {\mathfrak {g}}_{2}}$

En 1893, Élie Cartan publicó una nota en la que describía un conjunto abierto en dotado de una distribución bidimensional —es decir, un campo de subespacios bidimensionales del espacio tangente que varía suavemente— para el que el álgebra de Lie aparece como las simetrías infinitesimales. ^[2] Ese mismo año, en la misma revista, Engel observó lo mismo. Más tarde se descubrió que la distribución bidimensional está estrechamente relacionada con una bola que rueda sobre otra bola. El espacio de configuraciones de la bola que rueda es de cinco dimensiones, con una distribución bidimensional que describe los movimientos de la bola donde rueda sin resbalar ni torcerse. ^{[3] [4]}${\displaystyle \mathbb {C} ^{5}}$${\displaystyle {\mathfrak {g}}_{2}}$

En 1900, Engel descubrió que una forma trilineal antisimétrica genérica (o 3-forma) en un espacio vectorial complejo de 7 dimensiones se conserva mediante un grupo isomorfo a la forma compleja de G ₂ . ^[5]

En 1908, Cartan mencionó que el grupo de automorfismos de los octoniones es un grupo de Lie simple de 14 dimensiones. ^[6] En 1914 afirmó que esta es la forma real compacta de G ₂ . ^[7]

En libros y artículos más antiguos, G ₂ a veces se denota por E ₂ .

Hay tres álgebras de Lie reales simples asociadas con este sistema de raíces:

• El álgebra de Lie real subyacente del álgebra de Lie compleja G ₂ tiene dimensión 28. Tiene conjugación compleja como automorfismo externo y es simplemente conexa. El subgrupo compacto máximo de su grupo asociado es la forma compacta de G ₂ .
• El álgebra de Lie de la forma compacta tiene 14 dimensiones. El grupo de Lie asociado no tiene automorfismos externos ni centro y es simplemente conexo y compacto.
• El álgebra de Lie de la forma no compacta (dividida) tiene dimensión 14. El grupo de Lie simple asociado tiene un grupo fundamental de orden 2 y su grupo de automorfismo externo es el grupo trivial. Su subgrupo compacto máximo es SU(2) × SU(2)/(−1,−1) . Tiene una doble cobertura no algebraica que es simplemente conexa.

El diagrama de Dynkin para G ₂ está dado por .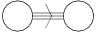

Su matriz de Cartan es:

${\displaystyle \left[{\begin{array}{rr}2&-3\\-1&2\end{array}}\right]}$

El sistema raíz de 12 vectores de G 2 en 2 dimensiones.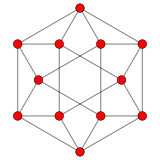

La proyección del plano de Coxeter A2 de los 12 vértices del cuboctaedro contiene la misma disposición vectorial 2D.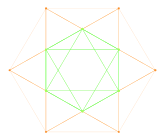

Gráfica de G2 como subgrupo de F4 y E8 proyectada en el plano de Coxeter

Un conjunto de raíces simples parase puede leer directamente de la matriz de Cartan anterior. Estas son (2, −3) y (−1, 2), sin embargo, la red entera generada por ellas no es la que se muestra arriba (por una razón obvia: la red hexagonal en el plano no se puede generar con vectores enteros). El diagrama anterior se obtiene a partir de un par de raíces diferente: y . ${\displaystyle \alpha =\left(1,0\right)}$${\textstyle \beta ={\sqrt {3}}\left(\cos {\frac {5\pi }{6}},\sin {\frac {5\pi }{6}}\right)={\frac {1}{2}}\left(-3,{\sqrt {3}}\right)}$

Las raíces restantes (positivas) son . ${\textstyle A=\alpha +\beta ,\,B=3\alpha +\beta ,\,\alpha +A=2\alpha +\beta \,\,{\rm {and}}\,\,\beta +B=3\alpha +2\beta }$

Aunque abarcan un espacio bidimensional, tal como se dibuja, es mucho más simétrico considerarlos como vectores en un subespacio bidimensional de un espacio tridimensional. En esta identificación, α corresponde a e₁−e₂, β a −e₁ + 2e₂−e₃, A a e₂−e₃, y así sucesivamente. En coordenadas euclidianas, estos vectores se ven de la siguiente manera:

El conjunto correspondiente de raíces simples es:

e₁−e₂ = (1,−1,0), y −e₁+2e₂−e₃ = (−1,2,−1)

Nota: α y A juntos forman un sistema de raíces idéntico a A₂ , mientras que el sistema formado por β y B es isomorfo a A₂ .

Su grupo de Weyl / Coxeter es el grupo diedro de orden 12. Tiene grado fiel mínimo .${\displaystyle G=W(G_{2})}$ ${\displaystyle D_{6}}$${\displaystyle \mu (G)=5}$

G ₂ es uno de los posibles grupos especiales que pueden aparecer como grupo de holonomía de una métrica de Riemann . Las variedades de holonomía G ₂ también se denominan G ₂ -variedades .

G ₂ es el grupo de automorfismos de los siguientes dos polinomios en 7 variables no conmutativas.

${\displaystyle C_{1}=t^{2}+u^{2}+v^{2}+w^{2}+x^{2}+y^{2}+z^{2}}$

${\displaystyle C_{2}=tuv+wtx+ywu+zyt+vzw+xvy+uxz}$(± permutaciones)

que proviene del álgebra de octoniones. Las variables deben ser no conmutativas, de lo contrario el segundo polinomio sería idénticamente cero.

Añadiendo una representación de los 14 generadores con coeficientes A , ...,  N se obtiene la matriz:

${\displaystyle A\lambda _{1}+\cdots +N\lambda _{14}={\begin{bmatrix}0&C&-B&E&-D&-G&F-M\\-C&0&A&F&-G+N&D-K&-E-L\\B&-A&0&-N&M&L&-K\\-E&-F&N&0&-A+H&-B+I&C-J\\D&G-N&-M&A-H&0&J&I\\G&K-D&-L&B-I&-J&0&-H\\-F+M&E+L&K&-C+J&-I&H&0\end{bmatrix}}}$

Es exactamente el álgebra de Lie del grupo

${\displaystyle G_{2}=\{g\in \mathrm {SO} (7):g^{*}\varphi =\varphi ,\varphi =\omega ^{123}+\omega ^{145}+\omega ^{167}+\omega ^{246}-\omega ^{257}-\omega ^{347}-\omega ^{356}\}}$

Hay 480 representaciones diferentes de correspondientes a las 480 representaciones de octoniones. La forma calibrada, tiene 30 formas diferentes y cada una tiene 16 variaciones con signo diferentes. Cada una de las variaciones con signo genera diferencias con signo de y cada una es un automorfismo de los 16 octoniones correspondientes. Por lo tanto, en realidad solo hay 30 representaciones diferentes de . Todas ellas se pueden construir con el álgebra de Clifford ^[8] utilizando una forma invertible para octoniones. Para otras variaciones con signo de , esta forma tiene residuos que clasifican otras 6 álgebras no asociativas que muestran simetría parcial. Una calibración análoga en conduce a sedeniones y al menos otras 11 álgebras relacionadas.${\displaystyle G_{2}}$${\displaystyle \varphi }$${\displaystyle G_{2}}$${\displaystyle G_{2}}$${\displaystyle 3e_{1234567}\pm \varphi }$${\displaystyle \varphi }$${\displaystyle G_{2}}$${\displaystyle \mathrm {Spin} (15)}$

Los caracteres de las representaciones de dimensión finita de las álgebras de Lie reales y complejas y de los grupos de Lie están dados por la fórmula de caracteres de Weyl . Las dimensiones de las representaciones irreducibles más pequeñas son (secuencia A104599 en la OEIS ):

1, 7, 14, 27, 64, 77 (dos veces), 182, 189, 273, 286, 378, 448, 714, 729, 748, 896, 924, 1254, 1547, 1728, 1729, 2079 (dos veces), 2261, 2926, 3003, 3289, 3542, 4096, 4914, 4928 (dos veces), 5005, 5103, 6630, 7293, 7371, 7722, 8372, 9177, 9660, 10206, 10556, 11571, 11648, 12096, 13090....

La representación de 14 dimensiones es la representación adjunta , y la de 7 dimensiones es la acción de G ₂ sobre los octoniones imaginarios.

Hay dos representaciones irreducibles no isomorfas de dimensiones 77, 2079, 4928, 30107, etc. Las representaciones fundamentales son aquellas con dimensiones 14 y 7 (correspondientes a los dos nodos en el diagrama de Dynkin en el orden tal que la triple flecha apunta del primero al segundo).

Vogan (1994) describió las representaciones irreducibles unitarias (de dimensión infinita) de la forma real dividida de G ₂ .

A la derecha se muestran las incrustaciones de los subgrupos máximos de G ₂ hasta la dimensión 77.

El grupo G ₂ ( q ) son los puntos del grupo algebraico G ₂ sobre el cuerpo finito F _q . Estos grupos finitos fueron introducidos por primera vez por Leonard Eugene Dickson en Dickson (1901) para q impar y Dickson (1905) para q par . El orden de G ₂ ( q ) es q ⁶ ( q ⁶ − 1)( q ² − 1) . Cuando q ≠ 2 , el grupo es simple , y cuando q = 2 , tiene un subgrupo simple de índice 2 isomorfo a ² A ₂ (3 ² ), y es el grupo de automorfismos de un orden máximo de los octoniones. El grupo de Janko J ₁ fue construido por primera vez como un subgrupo de G ₂ (11). Ree (1960) introdujo grupos de Ree retorcidos ² G ₂ ( q ) de orden q ³ ( q ³ + 1)( q − 1) para q = 3 ^{2 n +1} , una potencia impar de 3.

• Matriz de Cartan
• Diagrama de Dynkin
• Álgebra de Jordan excepcional
• Representación fundamental
• Estructura G2_​
• Grupo de mentiras
• Producto vectorial de siete dimensiones
• Grupo de mentiras simples
• Estrella de David

• Adams, J. Frank (1996), Conferencias sobre grupos de Lie excepcionales, Chicago Lectures in Mathematics, University of Chicago Press , ISBN 978-0-226-00526-3, Sr.  1428422
• Baez, John (2002), "Los octoniones", Bull. Amer. Math. Soc. , 39 (2): 145–205, arXiv : math/0105155 , doi :10.1090/S0273-0979-01-00934-X, S2CID  586512.

Consulte la sección 4.1: G ₂ ; una versión HTML en línea está disponible en http://math.ucr.edu/home/baez/octonions/node14.html.

• Bryant, Robert (1987), "Métricas con holonomía excepcional", Anales de matemáticas , 2, 126 (3): 525–576, doi :10.2307/1971360, JSTOR  1971360
• Dickson, Leonard Eugene (1901), "Teoría de grupos lineales en un campo arbitrario", Transactions of the American Mathematical Society , 2 (4), Providence, RI: American Mathematical Society : 363–394, doi : 10.1090/S0002-9947-1901-1500573-3 , ISSN  0002-9947, JSTOR  1986251, reimpreso en el volumen II de sus artículos recopiladosLeonard E. Dickson reportó grupos de tipo G ₂ en campos de características extrañas.
• Dickson, LE (1905), "Un nuevo sistema de grupos simples", Math. Ann. , 60 : 137–150, doi :10.1007/BF01447497, S2CID  179178145Leonard E. Dickson reportó grupos de tipo G ₂ en campos de características pares.
• Ree, Rimhak (1960), "Una familia de grupos simples asociados con el álgebra de Lie simple de tipo (G ₂ )", Boletín de la Sociedad Matemática Americana , 66 (6): 508–510, doi : 10.1090/S0002-9904-1960-10523-X , ISSN  0002-9904, MR  0125155
• Vogan, David A. Jr. (1994), "El dual unitario de G ₂ ", Inventiones Mathematicae , 116 (1): 677–791, Bibcode :1994InMat.116..677V, doi :10.1007/BF01231578, ISSN  0020-9910, MR  1253210, S2CID  120845135