Cuarto de tono
Intervalo musical
Cuarto de tono en C

Un cuarto de tono es un tono que se encuentra a medio camino entre las notas habituales de una escala cromática o un intervalo que es aproximadamente la mitad de ancho (oralmente o logarítmicamente) que un semitono , que a su vez es la mitad de un tono entero . Los cuartos de tono dividen la octava en 50 centésimas cada uno y tienen 24 tonos diferentes.

Trompeta con 3 válvulas normales y un cuarteo en la válvula de extensión (derecha)

Los cuartos de tono tienen sus raíces en la música del Medio Oriente y más específicamente en la música tradicional persa . [1] Sin embargo, la primera propuesta evidenciada de la escala de cuartos de tono igualmente templado , o 24 temperamentos iguales , fue hecha por los teóricos de la música del siglo XIX Heinrich Richter en 1823 [2] y Mikhail Mishaqa alrededor de 1840. [3] Los compositores que han escrito música utilizando esta escala incluyen: Pierre Boulez , Julián Carrillo , Mildred Couper , George Enescu , Alberto Ginastera , Gérard Grisey , lois Hába , Ljubica Marić , Charles Ives , Tristan Murail , Krzysztof Penderecki , Giacinto Scelsi , Ammar El Sherei , Karlheinz Stockhausen , Tui St. George Tucker , Ivan Wyschnegradsky , Iannis Xenakis y Seppe Gebruers (consulte la lista de piezas de cuartos de tono ).

Tipos

Sistemas de afinación de temperamento igual

El compositor Charles Ives eligió el acorde de cuatro notas anterior (C–D)tres cuartos en punto-GEORGIAtres cuartos en punto) como una buena posibilidad para un acorde "fundamental" en la escala de cuartos de tono, similar no a la tónica sino al acorde mayor de la tonalidad tradicional. [4]
Segundo punto muerto en C
Escala de 8 tet en C
Segunda mayor en do
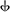La "séptima submenor": Btres cuartos planos= Unmedio afilado, 19 cuartos de tono. Se aproxima a la séptima armónica , B7♭ . Notación Maneri-Sims:B♭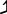

El término cuarto de tono puede referirse a varios intervalos diferentes, todos muy cercanos en tamaño. Por ejemplo, algunos teóricos de los siglos XVII y XVIII usaron el término para describir la distancia entre un sostenido y un bemol enarmónicamente distinto en temperamentos de tono medio (p. ej., D ♯ – E ♭ ). [2] En la escala de cuarto de tono, también llamada temperamento igual de 24 tonos (24-TET), el cuarto de tono es 50 centésimas , o una relación de frecuencia de 24 √ 2 o aproximadamente 1,0293, y divide la octava en 24 pasos iguales ( temperamento igual ). En esta escala, el cuarto de tono es el paso más pequeño . Un semitono se compone, por tanto, de dos pasos, y tres pasos forman tres cuartos de tono o segunda neutra , la mitad de una tercera menor . La escala 8-TET se compone de tres cuartos de tono. Cuatro pasos forman un tono entero.

Los cuartos de tono y los intervalos cercanos a ellos también aparecen en varios otros sistemas de afinación igualmente temperados. 22-TET contiene un intervalo de 54,55 centésimas, ligeramente más amplio que un cuarto de tono, mientras que 53-TET tiene un intervalo de 45,28 centésimas, ligeramente más pequeño. 72-TET también tiene cuartos de tono igualmente temperados, y de hecho contiene tres escalas de cuartos de tono, ya que 72 es divisible por 24. El intervalo más pequeño en 31 temperamento igual (la "diesis" de 38,71 centésimas) es medio semitono cromático , un tercio de un semitono diatónico y un quinto de un tono entero, por lo que puede funcionar como un cuarto de tono, un quinto tono o un sexto tono.

Sistemas de afinación de entonación justa

En la entonación justa, el cuarto de tono puede representarse por el cuarto de tono séptimal , 36:35 (48,77 centésimas), o por el cuarto de tono indecimal (es decir, el armónico trigésimo tercero ), 33:32 (53,27 centésimas), aproximadamente la mitad del semitono de 16:15 o 25:24. La relación de 36:35 es solo 1,23 centésimas más estrecha que un cuarto de tono de 24-TET. Esta relación justa es también la diferencia entre una tercera menor (6:5) y una tercera menor séptima (7:6).

El compositor Ben Johnston , para dar cabida al séptimo cuarto de tono, utiliza un pequeño "7" (7) como un accidente para indicar que una nota está bajada 49 centavos, o al revés "7" (7 al revés) para indicar que una nota se eleva 49 centésimas, [5] o una proporción de 36:35. [6] Johnston utiliza una flecha hacia arriba y hacia abajo para indicar que una nota se eleva o baja en una proporción de 33:32, o 53 centésimas. [6] El sistema de notación Maneri-Sims diseñado para 72-et utiliza las alteraciones accidentales.y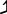para un cuarto de tono (36:35 o 48,77 cents) hacia arriba y hacia abajo.

Tocando cuartos de tono

Clarinete de cuarto de tono de Fritz Schüller visto desde cuatro lados.

Cualquier instrumento musical afinable puede utilizarse para tocar cuartos de tono, siempre que se utilicen dos intérpretes y dos instrumentos idénticos, uno de ellos afinado un cuarto de tono más alto. Como esto no requiere un instrumento especial ni técnicas especiales, mucha música a cuartos de tono se escribe para parejas de pianos, violines, arpas, etc. La afinación del instrumento y su posterior devolución a su tono anterior es fácil para los violines, más difícil para las arpas y lenta y relativamente cara para los pianos.

A continuación se aborda la capacidad de los instrumentos individuales para producir cuartos de tono. En los instrumentos occidentales, esto significa "además del sistema habitual de 12 tonos". Debido a que muchos instrumentos musicales fabricados en la actualidad (2018) están diseñados para la escala de 12 tonos, no todos son aptos para tocar cuartos de tono. A veces se deben utilizar técnicas de interpretación especiales.

Los instrumentos musicales convencionales que no pueden tocar cuartos de tono (excepto mediante técnicas especiales, ver a continuación) incluyen:

  • La mayoría de los instrumentos de teclado no electrónicos estándar o no modificados, como pianos , órganos y acordeones.
  • Instrumentos de cuerda con trastes , como guitarras , bajos y ukeleles (aunque en estos es posible tocar cuartos de tono mediante pitch-bending , con afinaciones especiales o con mástiles personalizados)
  • Instrumentos de percusión afinados , si se utilizan técnicas estándar y si los instrumentos no son afinables
  • Instrumentos de viento occidentales que utilizan llaves o válvulas.
    • Instrumentos de viento de madera , como clarinetes, saxofones, flautas y oboes (aunque con muchos de ellos, todavía es posible usar técnicas no estándar, como digitaciones especiales o que el intérprete manipule su embocadura , para tocar al menos algunos cuartos de tono, si no una escala completa )
    • Instrumentos de viento metal con válvulas ( trompeta , tuba ) (aunque, al igual que con los instrumentos de viento madera, la manipulación de la embocadura, así como los tonos armónicos que caen más cerca de los cuartos de tono que de los semitonos, hacen posibles las escalas de cuartos de tono; la técnica de la trompa de ajustar el tono con la mano derecha en la campana hace de este instrumento una excepción)
  • Armónica (aunque la flexión de notas es una técnica común)

Los instrumentos musicales convencionales que pueden tocar cuartos de tono incluyen

Se pueden utilizar otros instrumentos para reproducir cuartos de tono cuando se utilizan efectos de procesamiento de señales de audio, como el cambio de tono .

Se han construido pianos de cuarto de tono, que consisten esencialmente en dos pianos con dos teclados apilados uno sobre el otro en una única caja, uno afinado un cuarto de tono más alto que el otro. [ cita requerida ]

Música del Oriente Medio

Muchas dastgah persas y maqamat árabes contienen intervalos de tres cuartos de tono; a continuación se ofrece una breve lista de ellos. [8]

  1. Bayati ( español ): DEmedio planoFGAB ♭ CD
    \relativo c' { \tiempo 8/4 \omit Staff.TimeSignature d4 eeh fga bes cd \bar "|" }
  2. Rast ( español ):
    CDEmedio planoFGABmedio planoC (ascendente)
    CB ♭ AGFEmedio planoDC (descendente)
    \relativo c' { \tiempo 8/4 \omit Staff.TimeSignature c4 d eeh fga beh c \bar "|" }
  3. Saba ( español ): DEmedio planoFG ♭ AB ♭ CD
    \relative c' { \time 8/4 \omit Staff.TimeSignature d4 eeh f ges a bes cd \bar "|" }
  4. Sigah ( سه گاه ): Emedio planoFGABmedio planoCDEmedio plano
    \relative c' { \time 8/4 \omit Staff.TimeSignature eeh fga beh cd eeh \bar "|" }
  5. 'Ajam ( el Profeta )
  6. Manguito

El filósofo y científico islámico Al-Farabi describió una serie de intervalos en su obra musical, incluidos varios cuartos de tono.

Escala de música de la iglesia asiria/siríaca: [9]

  1. Qadmoyo (Bayati)
  2. Trayono (Husayni)
  3. Tlithoyo (Segah)
  4. Rbiʿoyo (Rast)
  5. Hmishoyo
  6. Shtithoyo ('Ajam)
  7. Shbiʿoyo
  8. Tminoyo

Escala de cuartos de tono

La escala de cuartos de tono, conocida como gadwal en árabe, [8] se desarrolló en Oriente Medio en el siglo XVIII y muchos de los primeros escritos detallados en Siria del siglo XIX describen la escala como de 24 tonos iguales. [10] La invención de la escala se atribuye a Mishaqa , quien escribió un libro dedicado al tema [11] pero dejó en claro que su maestro, el jeque Muhammad al-Attar (1764-1828), era uno de los muchos que ya estaban familiarizados con el concepto. [12]

\relative c' { \cadenzaOn \omit Staff.TimeSignature \tempo 1 = 90 \set Score.tempoHideNote = ##t c1 cih cis cisih d dih dis disih e eih f fih fis fisih g gih gis gisih a aih ais aisih b bih \barra "|" c\bar "|." \break c1 ceh b beh bes beseh a aeh aes aeseh g geh ges geseh f feh e eeh ees eeseh d deh des deseh \bar "|" c\bar "|." }

La escala de cuartos de tono puede ser principalmente una construcción teórica en la música árabe. El cuarto de tono proporciona a los músicos un "mapa conceptual" que pueden utilizar para analizar y comparar intervalos por número de cuartos de tono, y esta puede ser una de las razones por las que acompaña a un renovado interés en la teoría, siendo la instrucción en teoría musical un requisito generalizado desde ese período. [10]

Anteriormente, los tonos de un modo se elegían de una escala compuesta por diecisiete tonos, desarrollada por Safi al-Din al-Urmawi en el siglo XIII. [12]

19-Limite los intervalos de entonación aproximados en 24  TET

El compositor Charles Ives eligió el acorde C–Dmedio afilado–F–Gmedio afilado–B ♭ como buena posibilidad para un acorde “secundario” en la escala de cuartos de tono, similar al acorde menor de la tonalidad tradicional. Consideró que puede construirse sobre cualquier grado de la escala de cuartos de tono [4] Aquí está el “menor” secundario y su “primera inversión”:

\relative c' { \omit Staff.TimeSignature \set Score.tempoHideNote = ##t <c dih f gih bes>1 \bar "|" <cf gih bes dih>1 \bar "|." }

El descenso de graves de la versión de Nancy Sinatra de " These Boots Are Made for Walkin' " incluye descensos de cuartos de tono. [13] Varios álbumes de cuartos de tono han sido grabados por Jute Gyte, una banda unipersonal de black metal de vanguardia de Missouri, EE. UU. [14] [15] Otro álbum de metal de cuartos de tono fue publicado por la banda sueca Massive Audio Nerve. [16] Los álbumes de la banda australiana de rock psicodélico King Gizzard & the Lizard Wizard Flying Microtonal Banana , KG y LW enfatizan fuertemente los cuartos de tono y usaron una guitarra hecha a medida en afinación 24  TET . [17] El violinista/violista de jazz Mat Maneri , junto con su padre Joe Maneri , hizo un álbum de fusión crossover, Pentagon (2005), [18] que incluía experimentos en hip hop con pianos de cuarto de tono, así como texturas de órgano eléctrico y mellotron , junto con trombón distorsionado, en un tipo de jazz / rock mixto post-Bitches Brew . [19]

Más tarde, Seppe Gebruers comenzó a tocar e improvisar con dos pianos afinados a un cuarto de tono de distancia. En 2019 comenzó un proyecto de investigación en el Conservatorio Real de Gante , titulado 'Posibilidades inexploradas de la improvisación contemporánea y la influencia de la microtonalidad en el proceso de creación'. [20] Con dos pianos afinados a un cuarto de tono de distancia, Gebruers grabó 'The Room: Time & Space' (2018) en una formación de trío con el baterista Paul Lovens y el bajista Hugo Anthunes. En su proyecto en solitario 'Playing with standards' (lanzamiento del álbum en enero de 2023), Gebruers toca con canciones famosas, incluidos estándares de jazz. Con Paul Lytton y Nils Vermeulen forma un trío 'Playing with standards'.

Tetracordios griegos antiguos

El género enarmónico del tetracordio griego consistía en un ditono o una tercera mayor aproximada , y un semitono , que se dividía en dos microtonos . Aristóxenos , Dídimo y otros presentaron el semitono como dividido en dos intervalos aproximados de un cuarto de tono de aproximadamente el mismo tamaño, mientras que otros teóricos griegos antiguos describieron los microtonos resultantes de dividir el semitono del género enarmónico como desiguales en tamaño (es decir, uno más pequeño que un cuarto de tono y uno más grande). [21] [22]

Género enarmónico dórico griego: dos tetracordios disjuntos, cada uno de un cuarto de tono, un cuarto de tono y una tercera mayor.

Tamaño del intervalo en temperamento igual

A continuación se muestran los tamaños de algunos intervalos comunes en una escala igualmente temperada de 24 notas, con los nombres de intervalos propuestos por Alois Hába (tercera neutra, etc.) e Ivan Wyschnegradsky (cuarta mayor, etc.):

Nombre del intervaloTamaño
(pasos)		Tamaño
(centavos)		MIDIProporción justaSólo
(centavos)		MIDIError
(centavos)
octava2412002:11200.00+0 0.00
octava semidisminuida23115035:181151.23− 0 1,23
Séptimo supermayor23115027:141137.04+12,96
séptima mayor22110015:80​1088.27+11,73
séptima neutra , tono mayor21105011:60​1049.36+ 0 0,64
Séptima neutra , tono menor21105020:111035.00+15.00
séptima mayor solo menor2010009:51017.60−17,60
pequeña séptima menor20100016:90​0 996.09+ 0 3,91
sexta supermayor / séptima submenor190 9507:40 968,83-18,83
sexta mayor180 9005:30 884,36+15,64
Sexto neutro170 85018:110 852,59- 0 2,59
sexta menor160 8008:50 813,69-13,69
sexta submenor150 75014:90​0 764,92-14,92
quinta perfecta140 7003:20 701,96- 0 1,96
quinta menor130 65016:110 648,68+ 0 1,32
Tritono septimal menor120 6007:50 582,51+17,49
cuarta mayor110 55011:80​0 551,32- 0 1,32
cuarta perfecta100 5004:30 498,04+ 0 1,96
tercera mayor tridecimal0 90 45013:100 454,21− 0 4,21
septima tercera mayor0 90 4509:70 435,08+14,92
tercera mayor0 80 4005:40 386,31+13,69
tercio neutro indecimal0 70 35011:90​0 347,41+ 0 2,59
tercera menor0 60 3006:50 315,64-15,64
septimal tercera menor0 50 2507:60 266,87-16,87
cinco cuartos de tono tridecimal0 50 25015:130 247,74+ 0 2,26
septimal tono entero0 50 2508:70 231,17+18,83
segunda mayor , tono mayor0 40 2009:80 203,91− 0 3,91
segunda mayor , tono menor0 40 20010:9 00 182,40+17,60
Segundo neutro , mayor indecimal0 30 15011:100 165,00−15,00
Segundo neutro , indecimal menor0 30 15012:110 150,64− 0 0,64
15:14 semitono0 20 10015:140 119,44-19,44
semitono diatónico , justo0 20 10016:150 111,73-11,73
21:20 semitono0 20 10021:2000 84,47+15,53
28:27 semitono0 100 5028:2700 62,96-12,96
33:32 semitono0 100 5033:3200 53,27-3,27
unísono0 0000 01:1000 0.00+0 0.00

Pasar de 12-TET a 24-TET permite una mejor aproximación de varios intervalos. Los intervalos que coinciden particularmente bien incluyen la segunda neutra , la tercera neutra y la relación (11:8), o el undécimo armónico. La tercera menor séptima y la tercera mayor séptima se aproximan bastante mal; las relaciones (13:10) y (15:13), que involucran al decimotercer armónico, coinciden muy de cerca. En general, se puede considerar que 24-TET coincide más de cerca con los armónicos undécimo y decimotercero que con el séptimo.

Véase también

Referencias

  1. ^ Hormoz Farhat (2004). El concepto de dastgah en la música persa. Cambridge University Press. ISBN  0-521-54206-5
  2. ^ de Julian Rushton , "Quarter-Tone", The New Grove Dictionary of Music and Musicians , segunda edición, editado por Stanley Sadie y John Tyrrell (Londres: Macmillan, 2001).
  3. ^ Touma, Habib Hassan (1996). La música de los árabes , pág. 16. Traductor: Laurie Schwartz. Portland, Oregón: Amadeus Press. ISBN 0-931340-88-8 . 
  4. ^ ab Boatwright, Howard (1965). "Ives' Quarter-Tone Impressions", Perspectives of New Music 3, no. 2 (primavera-verano): pp. 22-31; citas en las pp. 27-28; reimpreso en Perspectives on American Composers , editado por Benjamin Boretz y Edward T. Cone , pp. 3-12, Nueva York: WW Norton, 1971, cita en las pp. 8-9. "Estos dos acordes delineados arriba podrían denominarse mayor y menor".
  5. ^ Douglas Keislar; Easley Blackwood ; John Eaton ; Lou Harrison ; Ben Johnston ; Joel Mandelbaum ; William Schottstaedt. pág. 193. "Seis compositores estadounidenses sobre afinaciones no estándar", Perspectives of New Music , vol. 29, núm. 1. (invierno de 1991), pp. 176-211.
  6. ^ ab Fonville, John (verano de 1991). "Ben Johnston's Extended Just Intonation: A Guide for Interpreters", pág. 114, Perspectives of New Music , vol. 29, núm. 2, págs. 106-137.
  7. ^ Sistema Kingma
  8. ^ ab Spector, Johanna (mayo de 1970). "Música clásica ʿUd en Egipto con especial referencia a Maqamat". Etnomusicología . 14 (2): 243–257. doi :10.2307/849799. JSTOR  849799.
  9. ^ Asaad, Gabriel (1990). La música siria a lo largo de la historia
  10. ^ ab Marcus, Scott (primavera-verano de 1993). "La interfaz entre la teoría y la práctica: la entonación en la música árabe". Asian Music . 24 (2): 39–58. doi :10.2307/834466. JSTOR  834466.
  11. ^ Mishaqa, Mikhiiʾil (c. 1840). al-Risāla al-shihābiyya fi 'l-ṣināʿa al-mūsīqiyya [ Ensayo sobre el arte de la música para el emir Shihāb ] (en árabe).
  12. ^ ab Maalouf, Shireen (octubre-diciembre de 2003). "Mikhiiʾil Mishiiqa: virtual fundador de la escala de veinticuatro cuartos de tono iguales". Journal of the American Oriental Society . 123 (4): 835–840. doi :10.2307/3589971. JSTOR  3589971.
  13. ^ Everett, Walter (2009). Los cimientos del rock . Oxford University Press. pág. 32. ISBN 9780195310238.
  14. ^ Tremblay, Dæv (3 de septiembre de 2014). "Yute Gyte - Resentimiento". canthisbecallmusic.com (reseña del álbum).
  15. ^ Gyte, Jute. Discontinuidades. jutegyte.bandcamp.com (álbum de música). (sitio comercial).
  16. ^ "El álbum Cancer Vulgaris de Massive Audio Nerve en julio". blabbermouth.net .
  17. ^ Huguenor, Mike (21 de agosto de 2017). "King Gizzard & the Lizard Wizard hablan sobre su nuevo álbum Flying Microtonal Banana". Guitar World (guitarworld.com) (entrevista) . Consultado el 27 de enero de 2021 .
  18. ^ Maneri, M .; Maneri, J. (2005). Pentágono (álbum de música).
  19. ^ Maneri, Mat (1 de diciembre de 2005). "Pentagon de Will Layman". PopMatters (crítica del álbum).
  20. ^ "Seppe Gebruers - Jugando con los estándares".
  21. ^ Chalmers, John H., Jr. (1993). Divisiones del tetracordio . Hanover, NH: Frog Peak Music. Capítulo 5, página 49. ISBN 0-945996-04-7.{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )
  22. ^ West, Martin L. (1992). Música griega antigua . Oxford, Reino Unido: Oxford University Press. ISBN 0-19-814975-1.

Lectura adicional

  • Bartolozzi, Bruno (1967). Nuevos sonidos para instrumentos de viento . Londres, Reino Unido / Nueva York, NY: Oxford University Press.
  • Bousted, Donald (otoño de 2002). "Microtonalidad, la flauta dulce y el manual de la flauta dulce de cuarto de tono". The Recorder Magazine . Vol. 22, núm. 3. págs. 99–102.
  • Bousted, Donald (otoño de 2005). "Recursos para el cuarto de tono: melodía". The Recorder Magazine . Vol. 25, núm. 3. págs. 88–91.
  • Caravan, Ronald R. (1979). Ejercicios y estudios preliminares sobre técnicas contemporáneas para clarinete: material introductorio para el estudio de multifónicos, cuartos de tono y variación del timbre . Oswego, NY: Ethos Publications.
  • Ellis, Don (1975). Quarter Tones: A text with musical examples, exercise, and etudes (Cuartos de tono: un texto con ejemplos musicales, ejercicios y estudios) . Plainview, NY: Harold Branch.
  • MacDonald, John (1822). Tratado sobre el sistema armónico que surge de las vibraciones de las divisiones alícuotas de las cuerdas . Londres, Reino Unido: T. Preston.
  • Möllendorff, Willi; Monzo, Joe (2001). Música con cuartos de tono: experiencias en el armonio bicromático . Estados Unidos: J. Monzo.
  • Rees, Carla (2007). "Eva Kingma y la flauta de cuarto de tono". Pan: The Flute Magazine . 26 (4): 23–29.
  • Rewoldt, Todd (2000). "Cuartos de tono altissimo para el saxofón alto". Saxophone Symposium . 25 : 56–69.
  • "cuarto de tono / 24-edo", TonalSoft.com
Obtenido de "https://es.wikipedia.org/w/index.php?title=Cuarto_de_tono&oldid=1240749784"