Azulejos cuadrados

Teselación regular del plano euclidiano

Azulejos cuadrados

Tipo	Azulejos regulares
Configuración de vértice	4.4.4.4 (o 4 ⁴ )
Configuración de la cara	V4.4.4.4 (o V4 ⁴ )
Símbolo(s) de Schläfli	{4,4} {∞}×{∞}
Símbolo(s) de Wythoff	4 \| 2 4
Diagrama(s) de Coxeter
Simetría	p4m , [4,4], (*442)
Simetría de rotación	p4 , [4,4] ⁺ , (442)
Dual	auto-dual
Propiedades	Vértice-transitivo , arista-transitivo , cara-transitivo

En geometría , el mosaico cuadrado , teselación cuadrada o cuadrícula cuadrada es un mosaico regular del plano euclidiano . Tiene el símbolo de Schläfli ${4,4},$ lo que significa que tiene 4 cuadrados alrededor de cada vértice . Conway lo llamó cuadrilla .

El ángulo interno del cuadrado es de 90 grados , por lo que cuatro cuadrados en un punto forman un total de 360 grados. Es una de las tres teselas regulares del plano . Las otras dos son la tesela triangular y la tesela hexagonal .

Coloraciones uniformes

Hay 9 coloraciones uniformes distintas de un mosaico cuadrado. Nombrando los colores por índices en los 4 cuadrados alrededor de un vértice: 1111, 1112(i), 1112(ii), 1122, 1123(i), 1123(ii), 1212, 1213, 1234. (i) casos tienen simetría de reflexión simple, y (ii) simetría de reflexión de deslizamiento. Tres se pueden ver en el mismo dominio de simetría como coloraciones reducidas: 1112 _i a partir de 1213, 1123 _i a partir de 1234, y 1112 _ii reducido a partir de 1123 _ii .

9 colores uniformes
1111	1212	1213	1112 _yo	1122

p4m (*442)		p4m (*442)		pmm (*2222)
1234	1123 _yo	1123 _ii	1112 _ii

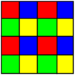pmm (*2222)		cmm (2*22)

Poliedros y teselaciones relacionados

Este teselado está relacionado topológicamente como parte de una secuencia de poliedros y teselados regulares, que se extienden hasta el plano hiperbólico : {4,p}, p=3,4,5...

* n 42 mutación de simetría de teselaciones regulares: {4, n } en a mi
Esférico	Euclidiano	Hiperbólica compacta				Paracompacto
{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8} ...	{4,∞}

Este teselado también está relacionado topológicamente como parte de una secuencia de poliedros regulares y teselados con cuatro caras por vértice, comenzando con el octaedro , con símbolo de Schläfli {n,4}, y diagrama de Coxeter., con n progresando hasta el infinito.

* n 42 mutación de simetría de teselaciones regulares: { n ,4} en a mi
Esférico		Euclidiano	Teselación hiperbólica

2 ⁴	3 ⁴	44	5 ⁴	6 ⁴	7 ⁴	8 ⁴	... ∞ ⁴

* n 42 mutaciones de simetría de teselaciones duales cuasirregulares: V (4.n) ²
Simetría *4n2 [n,4]	Esférico	Euclidiano	Hiperbólica compacta				Paracompacto	No compacto
Simetría *4n2 [n,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[iπ/λ,4]
Conferencia sobre alicatado .	V4.3.4.3	V4.4.4.4	V4.5.4.5	V4.6.4.6	V4.7.4.7	V4.8.4.8	V4.∞.4.∞	V4.∞.4.∞

* n 42 mutación de simetría de teselas expandidas: n .4.4.4 en a mi
Simetría [n,4], (* n 42)	Esférico	Euclidiano	Hiperbólica compacta				Paracomp.
Simetría [n,4], (* n 42)	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]	*∞42 [∞,4]
Cifras expandidas
Configuración.	3.4.4.4	4.4.4.4	5.4.4.4	6.4.4.4	7.4.4.4	8.4.4.4	∞.4.4.4
Configuración de figuras rómbicas .	V3.4.4.4	V4.4.4.4	V5.4.4.4	V6.4.4.4	V7.4.4.4	V8.4.4.4	V∞.4.4.4

Construcciones Wythoff a partir de teselas cuadradas

Al igual que los poliedros uniformes, hay ocho teselas uniformes que pueden basarse en la tesela cuadrada regular.

Si dibujamos los mosaicos coloreados de rojo en las caras originales, amarillo en los vértices originales y azul a lo largo de los bordes originales, las 8 formas son distintas. Sin embargo, si tratamos las caras de manera idéntica, solo hay tres formas topológicamente distintas: mosaico cuadrado , mosaico cuadrado truncado y mosaico cuadrado romo .

Teselación uniforme basada en simetría de teselación cuadrada en a mi
Simetría : [4,4], (*442)							[4,4] ⁺ , (442)	[4,4 ⁺ ], (4*2)


{4,4}	t{4,4}	r{4,4}	t{4,4}	{4,4}	rr{4,4}	tr{4,4}	sr{4,4}	s{4,4}
Duelos uniformes


V4.4.4.4	Versión 4.8.8	V4.4.4.4	Versión 4.8.8	V4.4.4.4	V4.4.4.4	Versión 4.8.8	V3.3.4.3.4

Teselación topológicamente equivalente

Se pueden realizar otros mosaicos cuadriláteros que sean topológicamente equivalentes al mosaico cuadrado (4 cuadriláteros alrededor de cada vértice).

Los mosaicos isoédricos tienen caras idénticas ( transitividad de caras ) y transitividad de vértices ; existen 18 variaciones, de las cuales 6 son triángulos que no se conectan de borde a borde o cuadriláteros con dos bordes colineales. La simetría dada supone que todas las caras son del mismo color. ^[1]

Teselación cuadrilátera isoédrica
Cuadrado p4m, (*442)	Rectángulo pmm, (*2222)	Paralelogramo p2, (2222)	Paralelogramo pmg, (22*)	Rombo cmm, (2*22)


Trapecio cmm, (2*22)	Cuadrilátero pgg, (22×)	Cometa pmg, (22*)	Cuadrilátero pgg, (22×)	Cuadrilátero p2, (2222)

Cuadriláteros degenerados o triángulos que no tienen aristas juntas
Isósceles pmg, (22*)	Isósceles pgg, (22×)		Pgg escaleno , (22×)		Escaleno p2, (2222)

Empaquetado circular

El mosaico cuadrado se puede utilizar como un empaquetamiento circular , colocando círculos de igual diámetro en el centro de cada punto. Cada círculo está en contacto con otros 4 círculos en el empaquetamiento ( número de besos ). ^[2] La densidad de empaquetamiento es π/4=78,54% de cobertura. Hay 4 coloraciones uniformes de los empaquetamientos circulares.

Apeirogones complejos regulares relacionados

Hay 3 apeirógonos complejos regulares que comparten los vértices del mosaico cuadrado. Los apeirógonos complejos regulares tienen vértices y aristas, donde las aristas pueden contener 2 o más vértices. Los apeirógonos regulares p{q}r están restringidos por: 1/ p + 2/ q + 1/ r = 1. Las aristas tienen p vértices y las figuras de vértices son r -gonales. ^[3]

Auto-dual	Duales

4{4}4 o	2{8}4 o	4{8}2 o

Véase también

Referencias

^ Teselación y patrones , de la lista de 107 teselación isoédrica, págs. 473-481
^ Orden en el espacio: un libro de referencia sobre diseño, Keith Critchlow, pág. 74-75, patrón circular 3
^ Coxeter, Politopos complejos regulares, págs. 111-112, pág. 136.

Coxeter, HSM Regular Polytopes , (3.ª edición, 1973), edición Dover, ISBN 0-486-61480-8 pág. 296, Tabla II: Panales regulares
Klitzing, Richard. "Teselación euclidiana 2D o4o4x - sentadilla - O1".
Williams, Robert (1979). La base geométrica de la estructura natural: un libro de consulta sobre diseño . Dover Publications, Inc. ISBN 0-486-23729-X.pág. 36
Grünbaum, Branko ; Shephard, GC (1987). Mosaicos y patrones . Nueva York: WH Freeman. ISBN 0-7167-1193-1.(Capítulo 2.1: Teselación regular y uniforme , págs. 58-65)
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 [1]

Enlaces externos

Weisstein, Eric W. "Cuadrícula cuadrada". MathWorld .
Weisstein, Eric W. "Teselación regular". MathWorld .
Weisstein, Eric W. "Teselación uniforme". MathWorld .

en a mi Panales fundamentales convexos regulares y uniformes en dimensiones 2–9
Espacio	Familia	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / / ${\tilde {F}}_{4}$ ${\tilde {E}}_{n-1}$
Y ²	Azulejos uniformes	0 _[3]	δ3	hδ3	qδ3	Hexagonal
Y ³	Panal de abeja convexo uniforme	0 _[4]	delta ₄	hδ4	qδ4
E4	Uniforme de 4 panales	0 _[5]	del ₅	hδ5	qδ5	Panal de abeja de 24 celdas
E ⁵	Uniforme de 5 panales	0 _[6]	delta ₆	hδ6	qδ6
E6	Uniforme de 6 panales	0 _[7]	delta ₇	hδ7	qδ7	2 ₂₂
E7	Uniforme de 7 panales	0 _[8]	del ₈	hδ8	qδ8	1 ₃₃ • 3 ₃₁
E8	Uniforme de 8 panales	0 _[9]	del ₉	hδ9	qδ9	1 ₅₂ • 2 ₅₁ • 5 ₂₁
E9	Uniforme de 9 panales	0 _[10]	delta ₁₀	hδ10	qδ10
E10	Uniforme de 10 panales	0 _[11]	delta ₁₁	hδ11	qδ11
En ^-1	Uniforme ( n -1)- panal	0 _{[ n ]}	delta _n	hδn	qδn	1 _k2 • 2 _k1 • k21

[1] Teselación y patrones , de la lista de 107 teselación isoédrica, págs. 473-481

[Critchlow-2] Orden en el espacio: un libro de referencia sobre diseño, Keith Critchlow, pág. 74-75, patrón circular 3

[3] Coxeter, Politopos complejos regulares, págs. 111-112, pág. 136.