Orden 4 mosaico hexagonal

Orden 4 mosaico hexagonal
Modelo de disco de Poincaré del plano hiperbólico
Tipo	Teselación regular hiperbólica
Configuración de vértice	6 4
Símbolo de Schläfli	{6,4}
Símbolo de Wythoff	4 | 6 2
Diagrama de Coxeter
Grupo de simetría	[6,4], (*642)
Dual	Orden de 6 mosaicos cuadrados
Propiedades	Vértice-transitivo , arista-transitivo , cara-transitivo

En geometría , la teselación hexagonal de orden 4 es una teselación regular del plano hiperbólico . Su símbolo de Schläfli es {6,4}.

Este mosaico representa un caleidoscopio hiperbólico de 6 espejos que definen un dominio fundamental de hexágono regular. Esta simetría por notación orbifold se llama *222222 con 6 intersecciones de espejos de orden 2. En la notación de Coxeter se puede representar como [6 ^* ,4], eliminando dos de los tres espejos (que pasan por el centro del hexágono). Agregar un espejo bisectorial a través de 2 vértices de un dominio fundamental hexagonal define una simetría trapezoidal *4422 . Agregar 3 espejos biseccionales a través de los vértices define la simetría *443 . Agregar 3 espejos biseccionales a través del borde define la simetría *3222 . Agregar las 6 bisectrices conduce a una simetría *642 completa .

*222222

*443

*3222

*642

Hay 7 coloraciones uniformes distintas para el mosaico hexagonal de orden 4. Son similares a 7 de las coloraciones uniformes del mosaico cuadrado , pero excluyen 2 casos con simetría giratoria de orden 2. Cuatro de ellos tienen construcciones reflexivas y diagramas de Coxeter , mientras que tres de ellos son subcoloraciones.

Construcciones uniformes de 6.6.6.6

	1 color	2 colores	3 y 2 colores		4, 3 y 2 colores
Coloración uniforme	(1111)	(1212)	(1213)	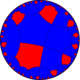(1113)	(1234)	(1123)	(1122)
Simetría	[6,4] ( *642 )	[6,6] ( *662 ) =	[(6,6,3)] = [6,6,1 + ] ( *663 ) =		[1 + ,6,6,1 + ] ( *3333 ) ==
Símbolo	{6,4}	r{6,6} = {6,4} 1 / 2	r(6,3,6) = r{6,6} 1 / 2		r{6,6} 1 / 4
Diagrama de Coxeter		=	=		==

La función regular {6,4} ₃ o {6,4} _(4,0) puede verse como una coloración de 4 colores en el mosaico {6,4}. También tiene una representación como un octaedro de Petrie , {3,4} ^π , un poliedro abstracto con vértices y aristas de un octaedro , pero en cambio conectados por 4 caras de polígonos de Petrie .

Este mosaico está relacionado topológicamente como parte de una secuencia de mosaicos regulares con caras hexagonales , comenzando con el mosaico hexagonal , con símbolo de Schläfli {6,n} y diagrama de Coxeter. , progresando hasta el infinito.

* n 62 mutación de simetría de teselaciones regulares: {6, n } en a mi
Esférico	Euclidiano	Teselación hiperbólica
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

Este teselado también está relacionado topológicamente como parte de una secuencia de poliedros regulares y teselados con cuatro caras por vértice, comenzando con el octaedro , con símbolo de Schläfli {n,4}, y diagrama de Coxeter., con n progresando hasta el infinito.

* n 42 mutación de simetría de teselaciones regulares: { n ,4} en a mi
Esférico		Euclidiano	Teselación hiperbólica
2 4	3 4	4 4	5 4	64	7 4	8 4	... ∞ 4

Mutación de simetría de teselaciones cuasirregulares: 6.n.6.n en a mi
Simetría *6n2 [n,6]	Euclidiano	Hiperbólica compacta					Paracompacto	No compacto
	*632 [3,6]	*642 [4,6]	*652 [5,6]	*662 [6,6]	*762 [7,6]	*862 [8,6]...	*∞62 [∞,6]	[iπ/λ,6]
Configuración de figuras cuasirregulares	6.3.6.3	6.4.6.4	6.5.6.5	6.6.6.6	6.7.6.7	6.8.6.8	6.∞.6.∞	6.∞.6.∞
Cifras duales
Configuración de figuras rómbicas	V6.3.6.3	V6.4.6.4	V6.5.6.5	V6.6.6.6	V6.7.6.7	V6.8.6.8	V6.∞.6.∞

Teselación tetrahexagonal uniforme en a mi
Simetría : [6,4], (*642 ) (con [6,6] (*662), [(4,3,3)] (*443), [∞,3,∞] (*3222) subsimetrías de índice 2) (Y [(∞,3,∞,3)] (*3232) subsimetría de índice 4)
= = =	=	= = =	=	= = =	=
{6,4}	t{6,4}	r{6,4}	t{4,6}	{4,6}	rr{6,4}	tr{6,4}
Duelos uniformes
V6 4	V4.12.12	V(4.6) 2	V6.8.8	V46	V4.4.4.6	V4.8.12
Alternancias
[1 + ,6,4] (*443)	[6 + ,4] (6*2)	[6,1 + ,4] (*3222)	[6,4 + ] (4*3)	[6,4,1 + ] (*662)	[(6,4,2 + )] (2*32)	[6,4] + (642)
=	=	=	=	=	=
h{6,4}	s{6,4}	hora{6,4}	s{4,6}	h{4,6}	hrr{6,4}	sr{6,4}

Teselación hexahexagonal uniforme en a mi
Simetría: [6,6], (*662)
= =	= =	= =	= =	= =	= =	= =
{6,6} = h{4,6}	t{6,6} = h2 { 4,6}	r{6,6} {6,4}	t{6,6} = h2 { 4,6}	{6,6} = h{4,6}	rr{6,6} r{6,4}	tr{6,6} t{6,4}
Duelos uniformes
V6 6	V6.12.12	V6.6.6.6	V6.12.12	V6 6	V4.6.4.6	V4.12.12
Alternancias
[1 + ,6,6] (*663)	[6 + ,6] (6*3)	[6,1 + ,6] (*3232)	[6,6 + ] (6*3)	[6,6,1 + ] (*663)	[(6,6,2 + )] (2*33)	[6,6] + (662)
=		=		=
h{6,6}	s{6,6}	hora{6,6}	s{6,6}	h{6,6}	hrr{6,6}	sr{6,6}

Teselación H2 similar en simetría *3232 en a mi
Diagramas de Coxeter
Figura de vértice	6 6		(3.4.3.4) 2		3.4.6.6.4		6.4.6.4
Imagen
Dual

Teselación uniforme en simetría *3222 en a mi
64	6.6.4.4	(3.4.4) 2	4.3.4.3.3.3
6.6.4.4	6.4.4.4	3.4.4.4.4
(3.4.4) 2	3.4.4.4.4	4 6

Wikimedia Commons alberga una categoría multimedia sobre Mosaico hexagonal de Orden-4 .

• Azulejos cuadrados
• Teselación de polígonos regulares
• Lista de teselados planos uniformes
• Lista de politopos regulares

• John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN  978-1-56881-220-5 (Capítulo 19, Las teselaciones hiperbólicas de Arquímedes)
• "Capítulo 10: Panales regulares en el espacio hiperbólico". La belleza de la geometría: doce ensayos . Publicaciones de Dover. 1999. ISBN 0-486-40919-8. Número de serie LCCN  99035678.

• Weisstein, Eric W. "Teselación hiperbólica". MathWorld .
• Weisstein, Eric W. "Disco hiperbólico de Poincaré". MathWorld .
• Galería de mosaicos hiperbólicos y esféricos
• KaleidoTile 3: Software educativo para crear mosaicos esféricos, planos e hiperbólicos
• Teselaciones planas hiperbólicas, Don Hatch