Hosoedro

Conjunto de hosoedros n -gonales regulares
Ejemplo de hosoedro hexagonal regular sobre una esfera
Tipo	Poliedro regular o teselación esférica
Caras	n digones
Bordes	norte
Vértices	2
Carácter de Euler.	2
Configuración de vértice	2 n
Símbolo de Wythoff	n | 2 2
Símbolo de Schläfli	{2, n }
Diagrama de Coxeter
Grupo de simetría	D n h [2,n] (*22n) orden 4 n
Grupo de rotación	D n [2,n] + (22n) orden 2 n
Poliedro dual	diedro n -gonal regular

En geometría esférica , un hosoedro n -gonal es una teselación de lunas sobre una superficie esférica , de modo que cada luna comparte los mismos dos vértices polares opuestos .

Un hosoedro n -gonal regular tiene el símbolo de Schläfli {2, n }, y cada lúmen esférico tiene un ángulo interno ⁠ 2π​/norte⁠ radianes ( ⁠360/norte⁠ grados). ^{[1] [2]}

Para un poliedro regular cuyo símbolo de Schläfli es { m ,  n }, el número de caras poligonales es:

${\displaystyle N_{2}={\frac {4n}{2m+2n-mn}}.}$

Los sólidos platónicos conocidos hasta la antigüedad son las únicas soluciones enteras para m ≥ 3 y n ≥ 3. La restricción m ≥ 3 impone que las caras poligonales deben tener al menos tres lados.

Al considerar los poliedros como un mosaico esférico , esta restricción puede relajarse, ya que los digones (2-gonos) pueden representarse como lunas esféricos , que tienen un área distinta de cero .

Permitiendo m = 2 hace

${\displaystyle N_{2}={\frac {4n}{2\times 2+2n-2n}}=n,}$

y admite una nueva clase infinita de poliedros regulares, que son los hosoedros. En una superficie esférica, el poliedro {2,  n } se representa como n contiguo a luna, con ángulos interiores de ⁠2π​/norte⁠ . Todos estos lunas esféricos comparten dos vértices comunes.

Un hosoedro trigonal regular, {2,3}, representado como una teselación de 3 lunas esféricos sobre una esfera.

Un hosoedro tetragonal regular, {2,4}, representado como una teselación de 4 lunas esféricos sobre una esfera.

Familia de hosoedros regulares · * n 22 mutaciones de simetría de teselaciones hosoédricas regulares: nn

Espacio	Esférico						Euclidiano
Nombre del mosaico	Hosoedro hexagonal	Hosoedro digonal	Hosoedro trigonal	Hosoedro cuadrado	Hosoedro pentagonal	...	Hosoedro apeirogonal
Imagen en mosaico						...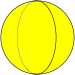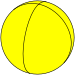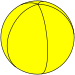
Símbolo de Schläfli	{2,1}	{2,2}	{2,3}	{2,4}	{2,5}	...	{2,∞}
Diagrama de Coxeter						...
Caras y aristas	1	2	3	4	5	...	∞
Vértices	2	2	2	2	2	...	2
Configuración de vértice .	2	2.2	2 3	2 4	2 5	...	2 ∞

Las caras esféricas digonales de la luna de un -hosoedro, , representan los dominios fundamentales de la simetría diedral en tres dimensiones : la simetría cíclica , , , orden . Los dominios de reflexión se pueden mostrar como imágenes especulares mediante lunas coloreadas alternativamente.${\estilo de visualización 2n}$${\estilo de visualización 2n}$$Estilo de visualización: 2,2n$$Estilo de visualización C_{nv}$${\estilo de visualización [n]}$${\estilo de visualización (*nn)}$${\estilo de visualización 2n}$

Al dividir cada luna en dos triángulos esféricos se crea una bipirámide -gonal , que representa la simetría diedral , el orden .${\estilo de visualización n}$ $Estilo de visualización D_{nh}}$${\estilo de visualización 4n}$

Diferentes representaciones de la simetría caleidoscópica de ciertos pequeños hosoedros

Simetría (orden )${\estilo de visualización 2n}$	Notación de Schönflies	$Estilo de visualización C_{nv}$	$Estilo de visualización C_{1v}$	$Estilo de visualización C_{2v}$	$Estilo de visualización C3v$	$Estilo de visualización C_{4v}$	$Estilo de visualización C_{5v}$	$Estilo de visualización C_{6v}}$
	Notación orbifold	${\estilo de visualización (*nn)}$	${\estilo de visualización (*11)}$	${\estilo de visualización (*22)}$	${\estilo de visualización (*33)}$	${\estilo de visualización (*44)}$	${\estilo de visualización (*55)}$	${\estilo de visualización (*66)}$
	Diagrama de Coxeter
		${\estilo de visualización [n]}$	${\estilo de visualización [\,\,]}$	${\estilo de visualización [2]}$	${\estilo de visualización [3]}$	${\estilo de visualización [4]}$	${\estilo de visualización [5]}$	${\estilo de visualización [6]}$
${\estilo de visualización 2n}$-hosoedro gonal	Símbolo de Schläfli	$Estilo de visualización: 2,2n$	${\estilo de visualización \{2,2\}}$	${\estilo de visualización \{2,4\}}$	${\estilo de visualización \{2,6\}}$	${\estilo de visualización \{2,8\}}$	${\estilo de visualización \{2,10\}}$	${\estilo de visualización \{2,12\}}$
	Dominios fundamentales coloreados alternativamente

El hosoedro tetragonal es topológicamente equivalente al sólido bicilindro de Steinmetz , la intersección de dos cilindros en ángulos rectos. ^[3]

El dual del hosoedro n-gonal {2,  n } es el diedro n -gonal { n , 2}. El poliedro {2,2} es autodual y es a la vez hosoedro y diedro.

Un hosoedro puede modificarse de la misma manera que los demás poliedros para producir una variación truncada . El hosoedro n -gonal truncado es el prisma n-gonal .

En el límite, el hosoedro se convierte en un hosoedro apeirogonal como una teselación bidimensional:

Los análogos multidimensionales en general se denominan hosótopos . Un hosótopo regular con símbolo de Schläfli {2, p ,..., q } tiene dos vértices, cada uno con una figura de vértice { p ,..., q }.

El hosótopo bidimensional , {2}, es un digión .

El término “hosohedro” parece derivar del griego ὅσος ( hosos ) “tantos”, siendo la idea de que un hosohedro puede tener “ tantas caras como se desee”. ^[4] Fue introducido por Vito Caravelli en el siglo XVIII. ^[5]

Wikimedia Commons alberga una categoría multimedia sobre Hosohedra .

• Poliedro
• Politopo

• McMullen, Peter ; Schulte, Egon (diciembre de 2002), Abstract Regular Polytopes (1.ª ed.), Cambridge University Press , ISBN 0-521-81496-0
• Coxeter, HSM , Politopos regulares (tercera edición), Dover Publications Inc., ISBN 0-486-61480-8 

• Weisstein, Eric W. "Hosohedro". MathWorld .