Proporción áurea
 | |
| Representaciones | |
|---|---|
| Decimal | 1.618 033 988 749 894 . . . [1] |
| Forma algebraica | |
| Fracción continua | |

En matemáticas , dos cantidades están en proporción áurea si su razón es la misma que la razón de su suma con la mayor de las dos cantidades. Expresado algebraicamente, para las cantidades y con , está en proporción áurea con si
donde la letra griega phi ( o ) denota la proporción áurea. [a] La constante satisface la ecuación cuadrática y es un número irracional con un valor de [1]
La proporción áurea fue llamada proporción extrema y media por Euclides , [2] y proporción divina por Luca Pacioli ; [3] y también tiene otros nombres. [b]
Los matemáticos han estudiado las propiedades de la proporción áurea desde la antigüedad. Es la relación entre la diagonal de un pentágono regular y su lado y, por lo tanto, aparece en la construcción del dodecaedro y el icosaedro . [7] Un rectángulo áureo , es decir, un rectángulo con una relación de aspecto de , puede cortarse en un cuadrado y un rectángulo más pequeño con la misma relación de aspecto . La proporción áurea se ha utilizado para analizar las proporciones de objetos naturales y sistemas artificiales como los mercados financieros , en algunos casos basándose en ajustes dudosos a los datos. [8] La proporción áurea aparece en algunos patrones de la naturaleza , incluida la disposición en espiral de las hojas y otras partes de la vegetación.
Algunos artistas y arquitectos del siglo XX , entre ellos Le Corbusier y Salvador Dalí , han proporcionado sus obras para aproximarse a la proporción áurea, creyendo que era estéticamente agradable. Estos usos suelen aparecer en forma de rectángulo áureo.
Cálculo
Dos cantidades y están en la proporción áurea si [9]
Por lo tanto, si queremos encontrar , podemos usar que la definición anterior se cumple para arbitrario ; por lo tanto, simplemente establecemos , en cuyo caso y obtenemos la ecuación , que se convierte en una ecuación cuadrática después de multiplicar por : que se puede reorganizar a
La fórmula cuadrática produce dos soluciones:
Dado que es una relación entre cantidades positivas, es necesariamente la raíz positiva. [10] La raíz negativa es, de hecho, la inversa negativa , que comparte muchas propiedades con la proporción áurea.
Historia
Según Mario Livio ,
Algunas de las mentes matemáticas más grandes de todas las épocas, desde Pitágoras y Euclides en la antigua Grecia , pasando por el matemático italiano medieval Leonardo de Pisa y el astrónomo renacentista Johannes Kepler , hasta figuras científicas actuales como el físico de Oxford Roger Penrose , han pasado interminables horas estudiando esta sencilla proporción y sus propiedades. ... Biólogos, artistas, músicos, historiadores, arquitectos, psicólogos e incluso místicos han reflexionado y debatido sobre la base de su ubicuidad y atractivo. De hecho, probablemente sea justo decir que la proporción áurea ha inspirado a pensadores de todas las disciplinas como ningún otro número en la historia de las matemáticas. [11]
— La proporción áurea: la historia de Phi, el número más asombroso del mundo
Los matemáticos de la antigua Grecia estudiaron por primera vez la proporción áurea debido a su frecuente aparición en geometría ; [12] la división de una línea en "razón extrema y media" (la sección áurea) es importante en la geometría de pentagramas y pentágonos regulares . [13] Según una historia, el matemático del siglo V a. C. Hipasus descubrió que la proporción áurea no era ni un número entero ni una fracción (es irracional ), sorprendiendo a los pitagóricos . [14] Los Elementos de Euclides ( c. 300 a. C. ) proporcionan varias proposiciones y sus pruebas empleando la proporción áurea, [15] [c] y contiene su primera definición conocida que procede de la siguiente manera: [16]
Se dice que una línea recta ha sido cortada en extrema y media razón cuando, como toda la línea es al segmento mayor, así es el mayor al menor. [17] [d]

La proporción áurea se estudió de forma periférica durante el siguiente milenio. Abu Kamil (c. 850–930) la empleó en sus cálculos geométricos de pentágonos y decágonos; sus escritos influyeron en los de Fibonacci (Leonardo de Pisa) (c. 1170–1250), quien utilizó la proporción en problemas de geometría relacionados, pero no observó que estuviera relacionada con los números de Fibonacci . [19]
Luca Pacioli tituló su libro Divina proporción ( 1509 ) en honor a la razón; el libro, en gran parte plagiado de Piero della Francesca , exploró sus propiedades, incluida su aparición en algunos de los sólidos platónicos . [20] [21] Leonardo da Vinci , quien ilustró el libro de Pacioli, llamó a la razón sectio aurea ('sección áurea'). [22] Aunque a menudo se dice que Pacioli abogó por la aplicación de la proporción áurea para producir proporciones agradables y armoniosas, Livio señala que la interpretación se ha rastreado hasta un error en 1799, y que Pacioli en realidad abogó por el sistema vitruviano de proporciones racionales. [23] Pacioli también vio un significado religioso católico en la razón, lo que llevó al título de su obra. Los matemáticos del siglo XVI como Rafael Bombelli resolvieron problemas geométricos utilizando la razón. [24]
El matemático alemán Simon Jacob (fallecido en 1564) observó que los números consecutivos de Fibonacci convergen hacia la proporción áurea; [25] esto fue redescubierto por Johannes Kepler en 1608. [26] La primera aproximación decimal conocida de la proporción áurea (inversa) fue enunciada como "aproximadamente " en 1597 por Michael Maestlin de la Universidad de Tubinga en una carta a Kepler, su antiguo alumno. [27] El mismo año, Kepler le escribió a Maestlin sobre el triángulo de Kepler , que combina la proporción áurea con el teorema de Pitágoras . Kepler dijo sobre estos:
La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras, el otro la división de una línea en razones extremas y medias. El primero lo podemos comparar con una masa de oro, el segundo lo podemos llamar una joya preciosa. [28]
Los matemáticos del siglo XVIII Abraham de Moivre , Nicolaus I Bernoulli y Leonhard Euler utilizaron una fórmula basada en la proporción áurea que encuentra el valor de un número de Fibonacci en función de su ubicación en la secuencia; en 1843, esta fórmula fue redescubierta por Jacques Philippe Marie Binet , por quien se la denominó "fórmula de Binet". [29] Martin Ohm utilizó por primera vez el término alemán goldener Schnitt ('sección áurea') para describir la proporción en 1835. [30] James Sully utilizó el término inglés equivalente en 1875. [31]
En 1910, el inventor Mark Barr comenzó a utilizar la letra griega phi ( ) como símbolo de la proporción áurea. [32] [e] También se ha representado con tau ( ), la primera letra del griego antiguo τομή ('corte' o 'sección'). [35]

El sistema de construcción zome , desarrollado por Steve Baer a finales de los años 1960, se basa en el sistema de simetría del icosaedro / dodecaedro y utiliza la proporción áurea de forma ubicua. Entre 1973 y 1974, Roger Penrose desarrolló el teselado de Penrose , un patrón relacionado con la proporción áurea tanto en la relación de áreas de sus dos teselas rómbicas como en su frecuencia relativa dentro del patrón. [36] Esto ganó interés después del descubrimiento de Dan Shechtman, ganador del Nobel en 1982, de cuasicristales con simetría icosaédrica, que poco después se explicaron a través de analogías con el teselado de Penrose. [37]
Matemáticas
Irracionalidad
La proporción áurea es un número irracional . A continuación se presentan dos breves pruebas de su irracionalidad:
Contradicción de una expresión en términos mínimos

Esta es una demostración por descendencia infinita . Recordemos que:
el todo es a la parte más larga como la parte más larga es a la parte más corta.
Si llamamos al todo y a la parte más larga , entonces la segunda afirmación anterior se convierte en
Decir que la proporción áurea es racional significa que es una fracción donde y son números enteros . Podemos tomar que está en términos mínimos y y como positivos . Pero si está en términos mínimos , entonces el igualmente valorado está en términos aún más bajos . Esa es una contradicción que se sigue del supuesto de que es racional .
Por irracionalidad de la raíz cuadrada de 5
Otra prueba breve –quizás más conocida– de la irracionalidad de la proporción áurea hace uso de la clausura de los números racionales bajo la adición y la multiplicación. Si se supone que es racional, entonces , la raíz cuadrada de , también debe ser racional. Esto es una contradicción ya que las raíces cuadradas de todos los números naturales no cuadrados son irracionales. [f]
Polinomio mínimo
La proporción áurea es también un número algebraico e incluso un entero algebraico . Tiene un polinomio mínimo .
Este polinomio cuadrático tiene dos raíces , y .
La proporción áurea también está estrechamente relacionada con el polinomio , que tiene raíces y . Como raíz de un polinomio cuadrático, la proporción áurea es un número construible . [38]
Proporción áurea conjugada y potencias
La raíz conjugada del polinomio mínimo es
El valor absoluto de esta cantidad ( ) corresponde a la relación de longitudes tomada en orden inverso (longitud del segmento más corto sobre la longitud del segmento más largo, ).
Esto ilustra la propiedad única de la proporción áurea entre los números positivos, que
o su inversa,
La relación polinomial cuadrática conjugada y definitoria conduce a valores decimales que tienen su parte fraccionaria en común con :
La secuencia de potencias de contiene estos valores , , , ; de manera más general, cualquier potencia de es igual a la suma de las dos potencias inmediatamente anteriores:
Como resultado, se puede descomponer fácilmente cualquier potencia de en un múltiplo de y una constante. El múltiplo y la constante son siempre números de Fibonacci adyacentes. Esto conduce a otra propiedad de las potencias positivas de :
Si , entonces:
Fracción continua y raíz cuadrada

La fórmula se puede expandir recursivamente para obtener una fracción continua simple para la proporción áurea: [39]
De hecho, es la forma más simple de una fracción continua, junto con su forma recíproca:
Los convergentes de estas fracciones continuas, , , , , , ... o , , , , , ... , son cocientes de números de Fibonacci sucesivos . Los términos consistentemente pequeños en su fracción continua explican por qué los aproximantes convergen tan lentamente . Esto hace que la proporción áurea sea un caso extremo de la desigualdad de Hurwitz para aproximaciones diofánticas , que establece que para cada irracional , hay infinitas fracciones distintas tales que,
Esto significa que la constante no se puede mejorar sin excluir la proporción áurea. Es, de hecho, el número más pequeño que debe excluirse para generar aproximaciones más cercanas de dichos números de Lagrange . [40]
Se puede obtener una forma de raíz cuadrada continua para de , dando como resultado: [41]
Relación con los números de Fibonacci y Lucas
Los números de Fibonacci y los números de Lucas tienen una relación intrincada con la proporción áurea. En la secuencia de Fibonacci, cada número es igual a la suma de los dos anteriores, comenzando con la secuencia base :
La secuencia de números de Lucas (que no debe confundirse con las secuencias de Lucas generalizadas , de las que ésta es parte) es como la secuencia de Fibonacci, en la que cada término es la suma de los dos anteriores, sin embargo comienza con :
Excepcionalmente, la proporción áurea es igual al límite de las razones de los términos sucesivos en la secuencia de Fibonacci y la secuencia de números de Lucas: [42]
En otras palabras, si un número de Fibonacci y Lucas se divide por su predecesor inmediato en la secuencia, el cociente se aproxima a . Por ejemplo,
Estas aproximaciones son alternativamente menores y mayores que , y convergen a a medida que aumentan los números de Fibonacci y Lucas.
Las expresiones de forma cerrada para las secuencias de Fibonacci y Lucas que involucran la proporción áurea son:
Combinando ambas fórmulas anteriores, se obtiene una fórmula para que involucra tanto los números de Fibonacci como los de Lucas:
Entre los números de Fibonacci y de Lucas se puede deducir , lo que simplifica expresar el límite del cociente de los números de Lucas por los números de Fibonacci como igual a la raíz cuadrada de cinco :
De hecho, hay afirmaciones mucho más contundentes:
Estos valores describen como una unidad fundamental del campo de números algebraicos .
Las potencias sucesivas de la proporción áurea obedecen a la recurrencia de Fibonacci , .
La reducción a una expresión lineal se puede lograr en un solo paso utilizando:
Esta identidad permite reducir cualquier polinomio en a una expresión lineal, como en:
Los números consecutivos de Fibonacci también se pueden utilizar para obtener una fórmula similar para la proporción áurea, aquí por suma infinita :
En particular, las potencias de se redondean a números de Lucas (en orden, excepto las dos primeras potencias, y , que están en orden inverso):
y así sucesivamente. [43] Los números de Lucas también generan directamente potencias de la proporción áurea; porque :
En su relación de interconexión con la proporción áurea se encuentra la noción de que la suma de terceros números de Fibonacci consecutivos es igual a un número de Lucas, es decir ; y , lo que es más importante , que .
Tanto la secuencia de Fibonacci como la secuencia de números de Lucas se pueden utilizar para generar formas aproximadas de la espiral áurea (que es una forma especial de una espiral logarítmica ) utilizando cuartos de círculo con radios de estas secuencias, que difieren solo ligeramente de la verdadera espiral logarítmica áurea. Espiral de Fibonacci es generalmente el término utilizado para espirales que se aproximan a espirales áureas utilizando cuadrados y cuartos de círculo de la secuencia de números de Fibonacci.
Geometría
La proporción áurea ocupa un lugar destacado en la geometría. Por ejemplo, está intrínsecamente implicada en la simetría interna del pentágono y se extiende hasta formar parte de las coordenadas de los vértices de un dodecaedro regular , así como de las de un sistema de 5 celdas . También aparece en el triángulo de Kepler y en los mosaicos de Penrose , así como en varios otros politopos .
Construcción
Dividir por división interior
- Teniendo un segmento de recta , construye una perpendicular en el punto , con la mitad de la longitud de . Dibuja la hipotenusa .
- Dibuja un arco con centro y radio . Este arco interseca la hipotenusa en el punto .
- Dibuja un arco con centro y radio . Este arco interseca el segmento de línea original en el punto . El punto divide el segmento de línea original en segmentos de línea y con longitudes en la proporción áurea.
Dividir por división exterior
- Dibuja un segmento de línea y construye a partir del punto un segmento perpendicular a y con la misma longitud que .
- Bisecar el segmento de línea con .
- Un arco circular alrededor de con radio interseca en el punto la línea recta que pasa por los puntos y (también conocida como la extensión de ). La razón de con el segmento construido es la proporción áurea.
Puedes ver ejemplos de aplicación en los artículos Pentágono con una longitud de lado dada , Decágono con una circunferencia circunscrita dada y Decágono con una longitud de lado dada .
Ambos algoritmos diferentes mostrados anteriormente producen construcciones geométricas que determinan dos segmentos de línea alineados donde la relación entre el más largo y el más corto es la proporción áurea.
Angulo dorado

Cuando dos ángulos que forman una circunferencia completa tienen medidas en proporción áurea, el menor se llama ángulo áureo , con medida :
Este ángulo se presenta en los patrones de crecimiento de las plantas como el espaciamiento óptimo de los brotes de hojas alrededor de los tallos de las plantas para que las hojas sucesivas no bloqueen la luz solar de las hojas que están debajo de ellas. [44]
Sistema de simetría pentagonal
Pentágono y pentagrama

En un pentágono regular, la razón entre una diagonal y un lado es la proporción áurea, mientras que las diagonales que se cortan se seccionan entre sí en la proporción áurea. Las propiedades de la proporción áurea de un pentágono regular se pueden confirmar aplicando el teorema de Ptolomeo al cuadrilátero formado al eliminar uno de sus vértices. Si el lado largo y las diagonales del cuadrilátero son , y los lados cortos son , entonces el teorema de Ptolomeo da . Dividiendo ambos lados por se obtiene (ver § Cálculo arriba),
Los segmentos diagonales de un pentágono forman un pentagrama , o polígono estrellado de cinco puntas , cuya geometría se describe esencialmente mediante . Básicamente, cada intersección de aristas secciona otras aristas en la proporción áurea. La relación entre la longitud del segmento más corto y el segmento delimitado por las dos aristas que se cruzan (es decir, un lado del pentágono invertido en el centro del pentagrama) es , como lo muestra la ilustración a cuatro colores.
La geometría pentagonal y pentagrammática nos permite calcular los siguientes valores para :
Triángulo dorado y gnomon dorado
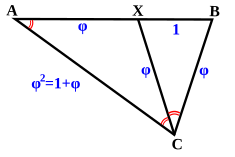
El triángulo formado por dos diagonales y un lado de un pentágono regular se llama triángulo áureo o triángulo sublime . Es un triángulo isósceles acutángulo con ángulo de vértice y ángulos de base . [45] Sus dos lados iguales están en proporción áurea con respecto a su base. [46] El triángulo formado por dos lados y una diagonal de un pentágono regular se llama gnomon áureo . Es un triángulo isósceles obtuso con ángulo de vértice y ángulo de base . Su base está en proporción áurea con respecto a sus dos lados iguales. [46] El pentágono puede, pues, subdividirse en dos gnomones áureos y un triángulo áureo central. Las cinco puntas de un pentagrama regular son triángulos áureos, [46] al igual que los diez triángulos formados al conectar los vértices de un decágono regular con su punto central. [47]
Al dividir en dos uno de los ángulos de la base del triángulo áureo, se obtiene un triángulo áureo más pequeño y un gnomon áureo. Análogamente, cualquier triángulo isósceles acutángulo puede subdividirse en un triángulo semejante y un triángulo isósceles obtuso, pero el triángulo áureo es el único en el que esta subdivisión se realiza mediante la bisectriz del ángulo, porque es el único triángulo isósceles cuyo ángulo de la base es el doble de su ángulo del vértice. La bisectriz del ángulo del triángulo áureo subdivide el lado que se encuentra con él en la proporción áurea, y las áreas de las dos partes subdivididas también están en la proporción áurea. [46]
Si el ángulo del vértice del gnomon áureo se triseca , el trisector lo subdivide a su vez en un gnomon áureo más pequeño y un triángulo áureo. El trisector subdivide la base en la proporción áurea, y las dos piezas tienen áreas en la proporción áurea. Análogamente, cualquier triángulo obtuso puede subdividirse en un triángulo semejante y un triángulo isósceles acutángulo, pero el gnomon áureo es el único para el que se realiza esta subdivisión mediante el trisector del ángulo, porque es el único triángulo isósceles cuyo ángulo del vértice es tres veces su ángulo de la base. [46]
Teselación de Penrose

La proporción áurea aparece de forma destacada en el mosaico de Penrose , una familia de mosaicos aperiódicos del plano desarrollados por Roger Penrose , inspirados en la observación de Johannes Kepler de que los pentagramas, decágonos y otras formas podrían llenar los huecos que las formas pentagonales dejan por sí solas cuando se unen entre sí. [48] Se han estudiado varias variaciones de este mosaico, todos cuyos prototipos exhiben la proporción áurea:
- La versión original de Penrose de este mosaico utilizaba cuatro formas: pentágonos y pentagramas regulares, figuras de "barco" con tres puntas de un pentagrama y rombos con forma de "diamante". [49]
- El sistema de mosaicos de Penrose de cometas y dardos utiliza cometas con tres ángulos interiores de y un ángulo interior de , y dardos, cuadriláteros cóncavos con dos ángulos interiores de , uno de , y un ángulo no convexo de . Unas reglas de coincidencia especiales restringen cómo pueden encontrarse las fichas en cualquier borde, lo que da como resultado siete combinaciones de fichas en cualquier vértice. Tanto las cometas como los dardos tienen lados de dos longitudes, en proporción áurea entre sí. Las áreas de estas dos formas de fichas también están en proporción áurea entre sí. [48]
- La cometa y el dardo pueden cortarse en sus ejes de simetría para formar un par de triángulos áureos y gnomones áureos, respectivamente. Con reglas de correspondencia adecuadas, estos triángulos, llamados en este contexto triángulos de Robinson , pueden usarse como prototipos para una forma de mosaico de Penrose. [48] [50]
- El mosaico rómbico de Penrose contiene dos tipos de rombos, un rombo delgado con ángulos de y , y un rombo grueso con ángulos de y . Todas las longitudes de los lados son iguales, pero la razón entre la longitud de los lados y la diagonal corta en el rombo delgado es igual a , al igual que la razón entre los lados de y la diagonal larga del rombo grueso. Al igual que con el mosaico de cometa y dardo, las áreas de los dos rombos están en proporción áurea entre sí. Nuevamente, estos rombos se pueden descomponer en pares de triángulos de Robinson. [48]
En triángulos y cuadriláteros
La construcción de Odom
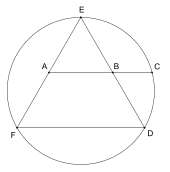
George Odom encontró una construcción para un triángulo equilátero : si el segmento de línea que une los puntos medios de dos lados se extiende para intersecar el círculo circunscrito , entonces los dos puntos medios y el punto de intersección con el círculo están en proporción áurea. [51]
Triángulo de Kepler
El triángulo de Kepler , llamado así en honor a Johannes Kepler , es el único triángulo rectángulo cuyos lados están en progresión geométrica : Las longitudes de estos lados son las tres medias pitagóricas de los dos números . Los tres cuadrados de sus lados tienen áreas en progresión geométrica áurea .
Entre los triángulos isósceles, la relación entre el radio interno y la longitud del lado se maximiza para el triángulo formado por dos copias reflejadas del triángulo de Kepler, que comparten el más largo de sus dos catetos. [52] El mismo triángulo isósceles maximiza la relación entre el radio de un semicírculo en su base y su perímetro . [53]
Para un triángulo de Kepler con la longitud lateral más pequeña , el área y los ángulos internos agudos son:
Rectángulo dorado
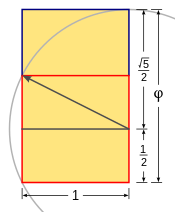
| Dibuja un cuadrado. |
| Dibuja una línea desde el punto medio de un lado del cuadrado hasta una esquina opuesta. |
| Utilice esa línea como radio para dibujar un arco que defina la altura del rectángulo. |
| Completa el rectángulo áureo. |
La proporción áurea proporciona las longitudes de los lados adyacentes de un rectángulo áureo en proporción . [54] Apilar rectángulos áureos produce rectángulos áureos de nuevo, y quitar o agregar cuadrados de rectángulos áureos deja rectángulos aún proporcionados en proporción . Pueden generarse mediante espirales áureas , a través de sucesivos cuadrados y cuartos de círculo del tamaño de los números de Fibonacci y Lucas. Aparecen de manera prominente en el icosaedro así como en el dodecaedro (ver la sección a continuación para más detalles). [55]
Rombo dorado
Un rombo áureo es un rombo cuyas diagonales son proporcionales a la proporción áurea, más comúnmente . [56] Para un rombo de tales proporciones, su ángulo agudo y sus ángulos obtusos son:
Las longitudes de sus diagonales corta y larga y , en términos de la longitud del lado son:
Su superficie, en términos de y :
Su radio interior , en términos de lado :
Los rombos áureos forman las caras del triacontaedro rómbico , los dos romboedros áureos , el dodecaedro de Bilinski , [57] y el hexecontaedro rómbico . [56]
Espiral dorada


Las espirales logarítmicas son espirales autosimilares donde las distancias recorridas por vuelta están en progresión geométrica . Una espiral logarítmica cuyo radio aumenta por un factor de la proporción áurea por cada cuarto de vuelta se llama espiral áurea . Estas espirales pueden aproximarse mediante cuartos de círculo que crecen según la proporción áurea, [59] o sus aproximaciones generadas a partir de los números de Fibonacci, [60] a menudo representados inscritos dentro de un patrón en espiral de cuadrados que crecen en la misma proporción. La forma espiral logarítmica exacta de la espiral áurea puede describirse mediante la ecuación polar con :
No todas las espirales logarítmicas están conectadas a la proporción áurea, y no todas las espirales conectadas a la proporción áurea tienen la misma forma que la espiral áurea. Por ejemplo, una espiral logarítmica diferente, que encierra una secuencia anidada de triángulos isósceles áureos, crece según la proporción áurea por cada vuelta que da, en lugar de según el ángulo de giro de la espiral áurea. [58] Otra variación, llamada la "espiral áurea mejorada", crece según la proporción áurea por cada media vuelta, en lugar de por cada cuarto de vuelta. [59]
Dodecaedro y icosaedro

| Coordenadas cartesianas del dodecaedro : | ||
| (±1, ±1, ±1) | ||
| (0, ± φ , ± 1/φ ) | ||
| (± 1/φ , 0, ± φ ) | ||
| (± φ , ± 1/φ , 0) | ||
| Un cubo anidado dentro del dodecaedro se representa con líneas de puntos . | ||
El dodecaedro regular y su poliedro dual, el icosaedro , son sólidos platónicos cuyas dimensiones están relacionadas con la proporción áurea. Un dodecaedro tiene caras pentagonales regulares, mientras que un icosaedro tiene triángulos equiláteros ; ambos tienen aristas . [61]
Para un dodecaedro de lado , el radio de una esfera circunscrita e inscrita, y el radio medio son ( , , y , respectivamente):
Mientras que para un icosaedro de lado , el radio de una esfera circunscrita e inscrita, y el radio medio son:
El volumen y el área de la superficie del dodecaedro se pueden expresar en términos de :
Así como para el icosaedro:
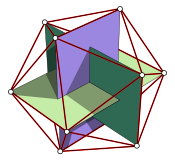
Estos valores geométricos se pueden calcular a partir de sus coordenadas cartesianas , que también se pueden obtener mediante fórmulas que involucran . Las coordenadas del dodecaedro se muestran en la figura anterior, mientras que las del icosaedro son las permutaciones cíclicas de:
Conjuntos de tres rectángulos áureos se intersecan perpendicularmente dentro de dodecaedros e icosaedros, formando anillos borromeos . [62] [55] En los dodecaedros, pares de vértices opuestos en rectángulos áureos se encuentran en los centros de las caras pentagonales, y en icosaedros, se encuentran en sus vértices. En total, los tres rectángulos áureos contienen vértices del icosaedro, o equivalentemente, intersecan los centros de las caras del dodecaedro. [61]
Un cubo puede inscribirse en un dodecaedro regular, con algunas de las diagonales de las caras pentagonales del dodecaedro sirviendo como aristas del cubo; por lo tanto, las longitudes de las aristas están en proporción áurea. El volumen del cubo es veces el del dodecaedro. [63] De hecho, los rectángulos áureos dentro de un dodecaedro están en proporciones áureas con un cubo inscrito, de modo que las aristas de un cubo y las aristas largas de un rectángulo áureo están en proporción áurea . Por otro lado, el octaedro , que es el poliedro dual del cubo, puede inscribir un icosaedro, de modo que los vértices de un icosaedro toquen las aristas de un octaedro en puntos que dividen sus aristas en proporción áurea. [64]
Otras propiedades
La expansión decimal de la proporción áurea se puede calcular mediante métodos de búsqueda de raíces, como el método de Newton o el método de Halley , en la ecuación o en (para calcular primero). El tiempo necesario para calcular dígitos de la proporción áurea utilizando el método de Newton es esencialmente , donde es la complejidad temporal de multiplicar dos números de dígitos. [65] Esto es considerablemente más rápido que los algoritmos conocidos para π y e . Una alternativa fácilmente programada utilizando solo aritmética de números enteros es calcular dos grandes números de Fibonacci consecutivos y dividirlos. La relación de los números de Fibonacci y , cada uno sobre dígitos, produce más de dígitos significativos de la proporción áurea. La expansión decimal de la proporción áurea [1] se ha calculado con una precisión de diez billones ( ) de dígitos. [66]
En el plano complejo , las raíces quintas de la unidad ( para un entero ) que satisfacen son los vértices de un pentágono. No forman un anillo de enteros cuadráticos , sin embargo, la suma de cualquier raíz quinta de la unidad y su conjugado complejo , es un entero cuadrático, un elemento de . Específicamente ,
Esto también es válido para las décimas raíces restantes de la unidad que satisfacen ,
Para la función gamma , las únicas soluciones de la ecuación son y .
Cuando se utiliza la proporción áurea como base de un sistema numérico (véase base de la proporción áurea , a veces denominada finaria o -naria ), los números enteros cuadráticos en el anillo –es decir, números de la forma para y en – tienen representaciones terminales , pero las fracciones racionales tienen representaciones no terminales.
La proporción áurea aparece también en la geometría hiperbólica , como la distancia máxima desde un punto de un lado de un triángulo ideal hasta el más cercano de los otros dos lados: esta distancia, la longitud del lado del triángulo equilátero formado por los puntos de tangencia de un círculo inscrito dentro del triángulo ideal, es . [67]
La proporción áurea aparece también en la teoría de funciones modulares . Para sea Entonces y donde y en la fracción continua debe evaluarse como . La función es invariante bajo , un subgrupo de congruencia del grupo modular . También para números reales positivos y tales que [68]
es un número de Pisot-Vijayaraghavan . [69]
Aplicaciones y observaciones

Arquitectura
El arquitecto suizo Le Corbusier , famoso por sus contribuciones al estilo internacional moderno , centró su filosofía del diseño en sistemas de armonía y proporción. La fe de Le Corbusier en el orden matemático del universo estaba estrechamente ligada a la proporción áurea y a la serie de Fibonacci, que describió como «ritmos evidentes a la vista y claros en sus relaciones entre sí. Y estos ritmos están en la raíz misma de las actividades humanas. Resuenan en el hombre con una inevitabilidad orgánica, la misma inevitabilidad sutil que hace que los niños, los ancianos, los salvajes y los eruditos tracen la Sección Áurea». [70] [71]
Le Corbusier utilizó explícitamente la proporción áurea en su sistema Modulor para la escala de proporciones arquitectónicas . Consideró que este sistema era una continuación de la larga tradición de Vitruvio , el " Hombre de Vitruvio " de Leonardo da Vinci , la obra de Leon Battista Alberti y otros que utilizaban las proporciones del cuerpo humano para mejorar la apariencia y la función de la arquitectura .
Además de la proporción áurea, Le Corbusier basó el sistema en medidas humanas , números de Fibonacci y la unidad doble. Llevó la sugerencia de la proporción áurea en proporciones humanas al extremo: seccionó la altura del cuerpo humano de su modelo a la altura del ombligo con las dos secciones en proporción áurea, luego subdividió esas secciones en proporción áurea en las rodillas y la garganta; utilizó estas proporciones de proporción áurea en el sistema Modulor . La Villa Stein en Garches de Le Corbusier de 1927 ejemplificó la aplicación del sistema Modulor. La planta rectangular de la villa, la elevación y la estructura interior se aproximan mucho a los rectángulos áureos. [72]
Otro arquitecto suizo, Mario Botta , basa muchos de sus diseños en figuras geométricas. Varias casas privadas que diseñó en Suiza están compuestas de cuadrados y círculos, cubos y cilindros. En una casa que diseñó en Origlio , la proporción áurea es la proporción entre la sección central y las secciones laterales de la casa. [73]
Arte

Las ilustraciones de poliedros de Leonardo da Vinci en la Divina proporción de Pacioli han llevado a algunos a especular sobre la posibilidad de que incorporara la proporción áurea en sus pinturas. Pero la sugerencia de que su Mona Lisa , por ejemplo, emplea proporciones de proporción áurea, no está respaldada por los propios escritos de Leonardo. [74] De manera similar, aunque el Hombre de Vitruvio de Leonardo se muestra a menudo en relación con la proporción áurea, las proporciones de la figura en realidad no coinciden con ella, y el texto solo menciona proporciones de números enteros. [75] [76]
Salvador Dalí , influenciado por las obras de Matila Ghyka , [77] utilizó explícitamente la proporción áurea en su obra maestra, El sacramento de la Última Cena . Las dimensiones del lienzo son un rectángulo áureo. Un enorme dodecaedro, en perspectiva de modo que los bordes parecen estar en proporción áurea entre sí, está suspendido por encima y detrás de Jesús y domina la composición. [74] [78]
Un estudio estadístico sobre 565 obras de arte de diferentes grandes pintores, realizado en 1999, encontró que estos artistas no habían utilizado la proporción áurea en el tamaño de sus lienzos. El estudio concluyó que la proporción media de los dos lados de las pinturas estudiadas es , con promedios para artistas individuales que van desde ( Goya ) a ( Bellini ). [79] Por otro lado, Pablo Tosto enumeró más de 350 obras de artistas conocidos, incluidas más de 100 que tienen lienzos con rectángulo áureo y proporciones, y otras con proporciones como , , , y . [80]

Libros y diseño
Según Jan Tschichold ,
Hubo una época en que las desviaciones de las proporciones verdaderamente hermosas de las páginas y de la sección áurea eran raras. Muchos libros publicados entre 1550 y 1770 muestran estas proporciones con exactitud, con una precisión de medio milímetro. [82]
Según algunas fuentes, la proporción áurea se utiliza en el diseño cotidiano, por ejemplo en las proporciones de naipes, postales, carteles, placas de interruptores de luz y televisores de pantalla ancha. [83]
Banderas

La relación de aspecto (ancho por alto) de la bandera de Togo fue pensada para ser la proporción áurea, según su diseñador. [84]
Música
Ernő Lendvai analiza las obras de Béla Bartók como si estuvieran basadas en dos sistemas opuestos, el de la proporción áurea y la escala acústica , [85] aunque otros estudiosos de la música rechazan ese análisis. [86] El compositor francés Erik Satie utilizó la proporción áurea en varias de sus piezas, incluyendo Sonneries de la Rose+Croix . La proporción áurea también es evidente en la organización de las secciones en la música de Reflets dans l'eau (Reflejos en el agua) de Debussy , de Images (1.ª serie, 1905), en la que «la secuencia de tonalidades está marcada por los intervalos 34, 21, 13 y 8, y el clímax principal se sitúa en la posición phi». [87]
El musicólogo Roy Howat ha observado que los límites formales de La Mer de Debussy corresponden exactamente a la sección áurea. [88] Trezise considera que la evidencia intrínseca es "notable", pero advierte que ninguna evidencia escrita o reportada sugiere que Debussy buscara conscientemente tales proporciones. [89]
Los teóricos de la música, entre ellos Hans Zender y Heinz Bohlen, han experimentado con la escala de 833 cents , una escala musical basada en el uso de la proporción áurea como intervalo musical fundamental . Cuando se mide en cents , una escala logarítmica para intervalos musicales, la proporción áurea es de aproximadamente 833,09 cents. [90]
Naturaleza

Johannes Kepler escribió que «la imagen del hombre y de la mujer proviene de la proporción divina. En mi opinión, la propagación de las plantas y los actos progenitores de los animales están en la misma proporción». [91]
El psicólogo Adolf Zeising observó que la proporción áurea aparecía en la filotaxis y argumentó a partir de estos patrones en la naturaleza que la proporción áurea era una ley universal. [92] Zeising escribió en 1854 sobre una ley ortogenética universal de "lucha por la belleza y la completitud en los reinos tanto de la naturaleza como del arte". [93]
Sin embargo, algunos han argumentado que muchas manifestaciones aparentes de la proporción áurea en la naturaleza, especialmente en lo que respecta a las dimensiones de los animales, son ficticias. [94]
Física
El ferroimán de Ising cuasi-unidimensional (niobato de cobalto) ha predicho estados de excitación (con simetría ) , que cuando se probaron con dispersión de neutrones, mostraron que sus dos más bajos estaban en proporción áurea. Específicamente, estas transiciones de fase cuántica durante la excitación de espín, que ocurren a una temperatura cercana al cero absoluto, mostraron pares de torceduras en su fase ordenada a cambios de espín en su fase paramagnética ; revelando, justo debajo de su campo crítico , una dinámica de espín con modos agudos a bajas energías que se acercan a la media áurea. [95]
Mejoramiento
No se conoce ningún algoritmo general para disponer un número dado de nodos de manera uniforme en una esfera, para ninguna de las diversas definiciones de distribución uniforme (véase, por ejemplo, el problema de Thomson o el problema de Tammes ). Sin embargo, una aproximación útil resulta de dividir la esfera en bandas paralelas de igual área de superficie y colocar un nodo en cada banda en longitudes espaciadas por una sección áurea del círculo, es decir, . Este método se utilizó para disponer los espejos del satélite participativo de estudiantes Starshine-3 . [96]
La proporción áurea también es un elemento fundamental para la búsqueda de la sección áurea .
Observaciones controvertidas
Algunos ejemplos de observaciones controvertidas de la proporción áurea incluyen los siguientes:

- A menudo se afirma que determinadas proporciones en los cuerpos de los vertebrados (incluidos los humanos) se encuentran en proporción áurea; por ejemplo, se ha dicho que la proporción de los huesos sucesivos de las falanges y los metacarpianos (huesos de los dedos) se aproxima a la proporción áurea. Sin embargo, existe una gran variación en las medidas reales de estos elementos en individuos específicos, y la proporción en cuestión a menudo es significativamente diferente de la proporción áurea. [97] [98]
- A menudo se afirma que las conchas de moluscos como el nautilus tienen proporción áurea. [99] El crecimiento de las conchas de nautilus sigue una espiral logarítmica , y a veces se afirma erróneamente que cualquier espiral logarítmica está relacionada con la proporción áurea, [100] o a veces se afirma que cada nueva cámara tiene proporción áurea en relación con la anterior. [101] Sin embargo, las mediciones de las conchas de nautilus no respaldan esta afirmación. [102]
- El historiador John Man afirma que tanto las páginas como el área de texto de la Biblia de Gutenberg estaban "basadas en la forma de la sección áurea". Sin embargo, según sus propias mediciones, la relación entre la altura y el ancho de las páginas es . [103]
- Los estudios de los psicólogos, comenzando por Gustav Fechner en 1876 [104] , se han diseñado para probar la idea de que la proporción áurea desempeña un papel en la percepción humana de la belleza . Si bien Fechner encontró una preferencia por las proporciones rectangulares centradas en la proporción áurea, los intentos posteriores de probar cuidadosamente tal hipótesis han sido, en el mejor de los casos, inconcluyentes. [105] [74]
- En el ámbito de las inversiones, algunos profesionales del análisis técnico utilizan la proporción áurea para indicar el soporte de un nivel de precio, o la resistencia a los aumentos de precio, de una acción o materia prima; después de cambios significativos de precio hacia arriba o hacia abajo, se supone que se encuentran nuevos niveles de soporte y resistencia en o cerca de los precios relacionados con el precio inicial a través de la proporción áurea. [106] El uso de la proporción áurea en las inversiones también está relacionado con patrones más complicados descritos por los números de Fibonacci (por ejemplo, el principio de onda de Elliott y el retroceso de Fibonacci ). Sin embargo, otros analistas de mercado han publicado análisis que sugieren que estos porcentajes y patrones no están respaldados por los datos. [107]
Pirámides egipcias

Los piramidólogos han analizado la Gran Pirámide de Giza (también conocida como la Pirámide de Keops o de Keops) como si tuviera un triángulo de Kepler doble como su sección transversal. Si esta teoría fuera cierta, la proporción áurea describiría la relación de las distancias desde el punto medio de uno de los lados de la pirámide hasta su vértice, y desde el mismo punto medio hasta el centro de la base de la pirámide. Sin embargo, la imprecisión en la medición causada en parte por la eliminación de la superficie exterior de la pirámide hace imposible distinguir esta teoría de otras teorías numéricas de las proporciones de la pirámide, basadas en pi o en proporciones de números enteros. El consenso de los eruditos modernos es que las proporciones de esta pirámide no se basan en la proporción áurea, porque tal base sería incoherente tanto con lo que se sabe sobre las matemáticas egipcias desde la época de la construcción de la pirámide, como con las teorías egipcias de la arquitectura y la proporción utilizadas en sus otras obras. [108]
El Partenón

Algunos afirman que la fachada del Partenón (c. 432 a. C.), así como algunos elementos de su fachada y de otros lugares, están circunscritos por rectángulos áureos. [110] Otros estudiosos niegan que los griegos tuvieran alguna asociación estética con la proporción áurea. Por ejemplo, Keith Devlin dice: "Ciertamente, la afirmación tan repetida de que el Partenón de Atenas se basa en la proporción áurea no está respaldada por mediciones reales. De hecho, toda la historia sobre los griegos y la proporción áurea parece carecer de fundamento". [111] Midhat J. Gazalé afirma que "no fue hasta Euclides... que se estudiaron las propiedades matemáticas de la proporción áurea". [112]
A partir de mediciones de 15 templos, 18 tumbas monumentales, 8 sarcófagos y 58 estelas funerarias del siglo V a. C. al siglo II d. C., un investigador concluyó que la proporción áurea estaba totalmente ausente de la arquitectura griega del siglo V a. C. clásico, y casi ausente durante los seis siglos siguientes. [113] Fuentes posteriores como Vitruvio (siglo I a. C.) discuten exclusivamente proporciones que pueden expresarse en números enteros, es decir, proporciones conmensurables en oposición a proporciones irracionales.
Arte moderno

La Section d'Or ('Sección áurea') fue un colectivo de pintores , escultores, poetas y críticos asociados con el cubismo y el orfismo . [114] Activos desde 1911 hasta alrededor de 1914, adoptaron el nombre tanto para resaltar que el cubismo representaba la continuación de una gran tradición, en lugar de ser un movimiento aislado, como en homenaje a la armonía matemática asociada con Georges Seurat . [115] (Varios autores han afirmado que Seurat empleó la proporción áurea en sus pinturas, pero los escritos y pinturas de Seurat sugieren que empleó proporciones simples de números enteros y cualquier aproximación a la proporción áurea fue coincidente). [116] Los cubistas observaron en sus armonías, la estructuración geométrica del movimiento y la forma, "la primacía de la idea sobre la naturaleza", "una absoluta claridad científica de concepción". [117] Sin embargo, a pesar de este interés general en la armonía matemática, es más difícil determinar si las pinturas que se exhibieron en la célebre exposición del Salón de la Sección de Oro de 1912 utilizaron la proporción áurea en alguna de sus composiciones. Livio, por ejemplo, afirma que no lo hicieron, [118] y Marcel Duchamp dijo lo mismo en una entrevista. [119] Por otro lado, un análisis sugiere que Juan Gris hizo uso de la proporción áurea al componer obras que probablemente, aunque no de manera definitiva, se exhibieron en la exposición. [119] [120] El historiador de arte Daniel Robbins ha argumentado que, además de hacer referencia al término matemático, el nombre de la exposición también se refiere al grupo anterior Bandeaux d'Or , con el que habían estado involucrados Albert Gleizes y otros ex miembros de la Abadía de Créteil . [121]
Se ha dicho que Piet Mondrian utilizó ampliamente la sección áurea en sus pinturas geométricas, [122] aunque otros expertos (incluido el crítico Yve-Alain Bois ) han desacreditado estas afirmaciones. [74] [123]
Véase también
- Lista de obras diseñadas con la proporción áurea
- Media metálica
- Relación de plástico
- Geometría sagrada
- Proporción superáurea
- Relación de plata
Referencias
Notas explicativas
- ^ Si se elimina la restricción de que y sean mayores que cero, entonces en realidad hay dos soluciones, una positiva y una negativa, para esta ecuación. se define como la solución positiva. La solución negativa es . La suma de las dos soluciones es , y el producto de las dos soluciones es .
- ^ Otros nombres incluyen la media áurea , sección áurea , [4] corte áureo , [5] proporción áurea , número áureo , [6] sección medial y sección divina .
- ^ Euclides, Elementos , Libro II, Proposición 11; Libro IV, Proposiciones 10-11; Libro VI, Proposición 30; Libro XIII, Proposiciones 1-6, 8-11, 16-18.
- ^ "῎Ακρον καὶ μέσον λόγον εὐθεῖα τετμῆσθαι λέγεται, ὅταν ᾖ ὡς ἡ ὅλη πρὸς τὸ μεῖζον τμῆμα, οὕτως τὸ μεῖζον πρὸς τὸ ἔλαττὸν." [18]
- ↑ En honor al escultor griego clásico Fidias (c. 490–430 a. C.); [33] Barr escribió más tarde que pensaba que era poco probable que Fidias realmente utilizara la proporción áurea. [34]
- ^ El teorema de que los números naturales no cuadrados tienen raíces cuadradas irracionales se puede encontrar en Elementos de Euclides , Libro X, Proposición 9.
Citas
- ^ abc Sloane, N. J. A. (ed.). "Secuencia A001622 (Expansión decimal de la proporción áurea phi (o tau) = (1 + sqrt(5))/2)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
- ^ Euclides. "Libro 6, Definición 3". Elementos .
- ^ Pacioli, Luca (1509). De divina proporción . Venecia: Luca Paganinem de Paganinus de Brescia (Antonio Capella).
- ^ Livio 2002, págs. 3, 81.
- ^ Summerson, John (1963). Heavenly Mansions and Other Essays on Architecture. Nueva York: WW Norton. p. 37.
Y lo mismo se aplica en arquitectura a los
rectángulos
que representan estas y otras proporciones (por ejemplo, el "corte áureo"). El único valor de estas proporciones es que son intelectualmente fructíferas y sugieren los ritmos del diseño modular.
- ^ Herz-Fischler 1998.
- ^ Herz-Fischler 1998, págs. 20-25.
- ^ Strogatz, Steven (24 de septiembre de 2012). "Yo, yo mismo y las matemáticas: control de proporciones". The New York Times .
- ^ Schielack, Vincent P. (1987). "La secuencia de Fibonacci y la proporción áurea". The Mathematics Teacher . 80 (5): 357–358. doi :10.5951/MT.80.5.0357. JSTOR 27965402.Esta fuente contiene una derivación elemental del valor de la proporción áurea.
- ^ Peters, JMH (1978). "Una relación aproximada entre π y la proporción áurea". The Mathematical Gazette . 62 (421): 197–198. doi :10.2307/3616690. JSTOR 3616690. S2CID 125919525.
- ^ Livio 2002, pág. 6.
- ^ Livio 2002, p. 4: "... división de líneas, que Euclides definió para... propósitos puramente geométricos..."
- ^ Livio 2002, págs. 7–8.
- ^ Livio 2002, págs. 4-5.
- ^ Livio 2002, pág. 78.
- ^ Hemenway, Priya (2005). Proporción divina: Phi en el arte, la naturaleza y la ciencia . Nueva York: Sterling. pp. 20-21. ISBN 9781402735226.
- ^ Livio 2002, pág. 3.
- ^ Euclides (2007). Elementos de geometría de Euclides . Traducido por Fitzpatrick, Richard. Lulu.com. p. 156. ISBN 978-0615179841.
- ^ Livio 2002, págs. 88–96.
- ^ Mackinnon, Nick (1993). "El retrato de Fra Luca Pacioli". The Mathematical Gazette . 77 (479): 130–219. doi :10.2307/3619717. JSTOR 3619717. S2CID 195006163.
- ^ Livio 2002, págs. 131-132.
- ^ Baravalle, HV (1948). "La geometría del pentágono y la sección áurea". Profesor de Matemáticas . 41 : 22–31. doi :10.5951/MT.41.1.0022.
- ^ Livio 2002, págs. 134-135.
- ^ Livio 2002, pág. 141.
- ^ Schreiber, Peter (1995). "Un suplemento al artículo de J. Shallit 'Orígenes del análisis del algoritmo euclidiano'". Historia Mathematica . 22 (4): 422–424. doi : 10.1006/hmat.1995.1033 .
- ^ Livio 2002, págs. 151-152.
- ^ O'Connor, John J.; Robertson, Edmund F. (2001). "La proporción áurea". Archivo de Historia de las matemáticas de MacTutor . Consultado el 18 de septiembre de 2007 .
- ^ Fink, Karl (1903). Breve historia de las matemáticas. Traducido por Beman, Wooster Woodruff; Smith, David Eugene (2.ª ed.). Chicago: Open Court. pág. 223.(Publicado originalmente como Geschichte der Elementar-Mathematik ).
- ^ Beutelspacher, Albrecht; Petri, Bernhard (1996). "Fibonacci-Zahlen". Der Goldene Schnitt . Einblick in die Wissenschaft (en alemán). Vieweg+Teubner Verlag. págs. 87–98. doi :10.1007/978-3-322-85165-9_6. ISBN 978-3-8154-2511-4.
- ^ Herz-Fischler 1998, págs. 167-170.
- ^ Posamentier y Lehmann 2011, pag. 8.
- ^ Posamentier y Lehmann 2011, pag. 285.
- ^ Cook, Theodore Andrea (1914). Las curvas de la vida. Londres: Constable. pág. 420.
- ^ Barr, Mark (1929). "Parámetros de belleza". Architecture (NY) . Vol. 60. pág. 325.Reimpreso: "Parámetros de belleza". Think . Vol. 10–11. IBM . 1944.
- ^ Livio 2002, pág. 5.
- ^ Gardner, Martin (2001). "7. Penrose Tiles". El libro colosal de las matemáticas . Norton. págs. 73–93.
- ^
Livio 2002, pp. 203–209 Gratias, Denis ; Quiquandon, Marianne (2019). "Descubrimiento de los cuasicristales: los primeros días". Comptes Rendus Physique . 20 (7–8): 803–816. Bibcode :2019CRPhy..20..803G. doi : 10.1016/j.crhy.2019.05.009 . S2CID 182005594.
Jaric, Marko V. (1989). Introducción a las matemáticas de los cuasicristales . Academic Press. p. x. ISBN 9780120406029Aunqueen el momento del descubrimiento de los cuasicristales la teoría de las funciones cuasiperiódicas ya se conocía desde hacía casi sesenta años, fueron las matemáticas de los teselaciones aperiódicas de Penrose, desarrolladas principalmente por Nicolaas de Bruijn , las que proporcionaron la mayor influencia en el nuevo campo.
Goldman, Alan I.; Anderegg, James W.; Besser, Matthew F.; Chang, Sheng-Liang; Delaney, Drew W.; Jenks, Cynthia J .; Kramer, Matthew J.; Lograsso, Thomas A.; Lynch, David W.; McCallum, R. William; Shield, Jeffrey E.; Sordelet, Daniel J.; Thiel, Patricia A. (1996). "Materiales cuasicristalinos". Científico estadounidense . 84 (3): 230–241. JSTOR 29775669. - ^ Martin, George E. (1998). Construcciones geométricas . Textos de pregrado en matemáticas. Springer. pp. 13-14. doi :10.1007/978-1-4612-0629-3. ISBN . 978-1-4612-6845-1.
- ^ Hailperin, Max; Kaiser, Barbara K.; Knight, Karl W. (1999). Abstracciones concretas: una introducción a la informática con Scheme. Brooks/Cole. pág. 63.
- ^ Hardy, GH ; Wright, EM (1960) [1938]. "§11.8. La medida de las aproximaciones más cercanas a un irracional arbitrario" . Introducción a la teoría de números (4.ª ed.). Oxford University Press. pp. 163–164. ISBN 978-0-19-853310-8.
- ^ Sizer, Walter S. (1986). "Raíces continuas". Revista de Matemáticas . 59 (1): 23–27. doi :10.1080/0025570X.1986.11977215. JSTOR 2690013. MR 0828417.
- ^ Tattersall, James Joseph (1999). Teoría elemental de números en nueve capítulos . Cambridge University Press. pág. 28.
- ^ Parker, Matt (2014). Cosas que se pueden hacer y crear en la cuarta dimensión . Farrar, Straus y Giroux. pág. 284. ISBN 9780374275655.
- ^ King, S.; Beck, F.; Lüttge, U. (2004). "Sobre el misterio del ángulo áureo en la filotaxis". Planta, célula y medio ambiente . 27 (6): 685–695. Bibcode :2004PCEnv..27..685K. doi :10.1111/j.1365-3040.2004.01185.x.
- ^ Fletcher, Rachel (2006). "La sección áurea". Nexus Network Journal . 8 (1): 67–89. doi : 10.1007/s00004-006-0004-z . S2CID 120991151.
- ^ abcde Loeb, Arthur (1992). "El triángulo dorado". Conceptos e imágenes: matemáticas visuales . Birkhäuser. págs. 179-192. doi :10.1007/978-1-4612-0343-8_20. ISBN . 978-1-4612-6716-4.
- ^ Miller, William (1996). "Pentágonos y triángulos áureos". Matemáticas en la escuela . 25 (4): 2–4. JSTOR 30216571.
- ^ abcd Grünbaum, Branko ; Shephard, GC (1987). Mosaicos y patrones. Nueva York: WH Freeman. págs. 537–547. ISBN 9780716711933.
- ^ Penrose, Roger (1978). "Pentaplexidad". Eureka . Vol. 39. pág. 32.(PDF original)
- ^ Frettlöh, D.; Harriss, E.; Gähler, F. "Triángulo de Robinson". Enciclopedia de mosaicos .
Clason, Robert G (1994). "Una familia de patrones de mosaicos de triángulos dorados". The Mathematical Gazette . 78 (482): 130–148. doi :10.2307/3618569. JSTOR 3618569. S2CID 126206189.
- ^ Odom, George; van de Craats, Jan (1986). "E3007: La proporción áurea a partir de un triángulo equilátero y su circunferencia circunscrita". Problemas y soluciones. The American Mathematical Monthly . 93 (7): 572. doi :10.2307/2323047. JSTOR 2323047.
- ^ Busard, Hubert LL (1968). "L'algèbre au Moyen Âge: le" Liber mensurationum "d'Abû Bekr". Journal des Savants (en francés y latín). 1968 (2): 65-124. doi :10.3406/jds.1968.1175.Véase el problema 51, reproducido en la pág. 98.
- ^ Bruce, Ian (1994). "Otra instancia del triángulo rectángulo áureo" (PDF) . Fibonacci Quarterly . 32 (3): 232–233. doi :10.1080/00150517.1994.12429219.
- ^ Posamentier y Lehmann 2011, pag. 11.
- ^ ab Burger, Edward B.; Starbird, Michael P. (2005) [2000]. El corazón de las matemáticas: una invitación al pensamiento eficaz (2.ª ed.). Springer. pág. 382. ISBN 9781931914413.
- ^ ab Grünbaum, Branko (1996). "Un nuevo hexecontaedro rómbico" (PDF) . Geombinatorics . 6 (1): 15–18.
- ^ Senechal, Marjorie (2006). "Donald y los romboedros dorados". En Davis, Chandler; Ellers, Erich W. (eds.). El legado de Coxeter . American Mathematical Society. págs. 159-177. ISBN 0-8218-3722-2.
- ^ ab Loeb, Arthur L.; Varney, William (marzo de 1992). "¿Existe la espiral áurea y, si no, dónde está su centro?". En Hargittai, István; Pickover, Clifford A. (eds.). Simetría espiral . World Scientific. págs. 47–61. doi :10.1142/9789814343084_0002. ISBN . 978-981-02-0615-4.
- ^ de Reitebuch, Ulrich; Skrodzki, Martin; Polthier, Konrad (2021). "Aproximación de espirales logarítmicas mediante cuartos de círculo". En Swart, David; Farris, Frank; Torrence, Eve (eds.). Actas de Bridges 2021: Matemáticas, arte, música, arquitectura, cultura . Phoenix, Arizona: Tessellations Publishing. págs. 95–102. ISBN 978-1-938664-39-7.
- ^ Diedrichs, Danilo R. (febrero de 2019). "Espirales de Arquímedes, logarítmicas y de Euler: patrones intrigantes y ubicuos en la naturaleza". The Mathematical Gazette . 103 (556): 52–64. doi :10.1017/mag.2019.7. S2CID 127189159.
- ^ ab Livio (2002, págs. 70–72)
- ^ Gunn, Charles; Sullivan, John M. (2008). "Los anillos borromeos: un vídeo sobre el nuevo logo de IMU". En Sarhangi, Reza; Séquin, Carlo H. (eds.). Actas de Puentes 2008 . Leeuwarden, Países Bajos. Publicaciones Tarquin. págs. 63–70.; Vídeo en "Los anillos borromeos: un nuevo logo para la IMU". Unión Matemática Internacional . Archivado desde el original el 8 de marzo de 2021.
- ^ Hume, Alfred (1900). "Algunas proposiciones sobre el dodecaedro regular". The American Mathematical Monthly . 7 (12): 293–295. doi :10.2307/2969130. JSTOR 2969130.
- ^ Coxeter, HSM ; du Val, Patrick ; Flather, HT; Petrie, JF (1938). Los cincuenta y nueve icosaedros . Vol. 6. Estudios de la Universidad de Toronto. p. 4.
Así como un tetraedro puede inscribirse en un cubo, un cubo puede inscribirse en un dodecaedro. Por reciprocidad, esto conduce a un octaedro circunscrito a un icosaedro. De hecho, cada uno de los doce vértices del icosaedro divide una arista del octaedro según la "sección áurea".
- ^ Muller, JM (2006). Funciones elementales: algoritmos e implementación (2.ª ed.). Boston: Birkhäuser. pág. 93. ISBN 978-0817643720.
- ^ Yee, Alexander J. (13 de marzo de 2021). "Récords establecidos por y-cruncher". numberword.org .Dos cálculos independientes realizados por Clifford Spielman.
- ^ Horocycles exinscrits: une propriété hyperbolique remarquable, cabri.net, consultado el 21 de julio de 2009.
- ^ Berndt, Bruce C.; Chan, Heng Huat; Huang, Sen-Shan; Kang, Soon-Yi; Sohn, Jaebum; Son, Seung Hwan (1999). "La fracción continua de Rogers-Ramanujan" (PDF) . Revista de Matemática Computacional y Aplicada . 105 (1–2): 9–24. doi :10.1016/S0377-0427(99)00033-3. Archivado desde el original (PDF) el 2022-10-06 . Consultado el 2022-11-29 .
- ^ Duffin, Richard J. (1978). "Algoritmos para localizar raíces de un polinomio y los números de Pisot Vijayaraghavan". Revista del Pacífico de Matemáticas . 74 (1): 47–56. doi : 10.2140/pjm.1978.74.47 .
- ^ Le Corbusier, El Modulor , p. 25 , citado en Padovan, Richard (1999). Proporción: ciencia, filosofía, arquitectura . Taylor & Francis. p. 316. doi :10.4324/9780203477465. ISBN 9781135811112.
- ^ Frings, Marcus (2002). "La sección áurea en la teoría arquitectónica". Nexus Network Journal . 4 (1): 9–32. doi : 10.1007/s00004-001-0002-0 . S2CID 123500957.
- ^ Le Corbusier, El Modulor , p. 35 , citado en Padovan, Richard (1999). Proporción: ciencia, filosofía, arquitectura . Taylor & Francis. p. 320. doi :10.4324/9780203477465. ISBN 9781135811112
Tanto las pinturas como los diseños arquitectónicos hacen uso de la sección áurea
. - ^ Urwin, Simon (2003). Análisis de la arquitectura (2.ª ed.). Routledge. págs. 154-155.
- ^ abcd Livio, Mario (2002). «La proporción áurea y la estética». Revista Plus . Consultado el 26 de noviembre de 2018 .
- ^ Devlin, Keith (2007). "El mito que no desaparecerá". Archivado del original el 12 de noviembre de 2020. Consultado el 26 de septiembre de 2013.
Parte del proceso para convertirse en un escritor de matemáticas es, al parecer, aprender que no se puede hacer referencia a la proporción áurea sin que después de la primera mención aparezca una frase que diga algo como "los antiguos griegos y otros creían que tenía propiedades divinas y místicas". Casi tan compulsiva es la necesidad de añadir un segundo dato del tipo "Leonardo Da Vinci creía que la forma humana muestra la proporción áurea". No hay ni una pizca de evidencia que respalde ninguna de las dos afirmaciones, y todas las razones para suponer que ambas son falsas. Sin embargo, ambas afirmaciones, junto con varias otras de la misma índole, siguen vigentes.
- ^ Simanek, Donald E. "Fibonacci Flim-Flam". Archivado desde el original el 9 de enero de 2010. Consultado el 9 de abril de 2013 .
- ^ Salvador Dalí (2008). La dimensión Dalí: descifrando la mente de un genio (DVD) . Media 3.14-TVC-FGSD-IRL-AVRO.
- ^ Hunt, Carla Herndon; Gilkey, Susan Nicodemus (1998). Enseñanza de las matemáticas en el bloque . Eye On Education. págs. 44, 47. ISBN 1-883001-51-X.
- ^ Olariu, Agata (1999). "Sección áurea y el arte de la pintura". arXiv : physics/9908036 .
- ^ Tosto, Pablo (1969). La composición áurea en las artes plásticas [ La composición dorada en las artes plásticas ] (en español). Hachette. págs. 134-144.
- ^ Tschichold, Jan (1991). La forma del libro. Hartley & Marks. pág. 43. Fig. 4. ISBN 0-88179-116-4.
Marco de proporciones ideales en un manuscrito medieval sin columnas múltiples. Determinado por Jan Tschichold en 1953. Proporción de página 2:3. Proporción de márgenes 1:1:2:3. Área de texto proporcionada según la sección áurea. La esquina exterior inferior del área de texto también está fijada por una diagonal.
- ^ Tschichold, Jan (1991). La forma del libro. Hartley & Marks. pp. 27-28. ISBN 0-88179-116-4.
- ^ Jones, Ronald (1971). "La sección áurea: una medida extraordinaria". The Structurist . 11 : 44–52.
¿Quién sospecharía, por ejemplo, que las placas de los interruptores de luz individuales están estandarizadas en términos de un rectángulo áureo?
Johnson, Art (1999). Problemas famosos y sus matemáticos . Teacher Ideas Press. pág. 45. ISBN 9781563084461La proporción áurea
es una característica estándar de muchos diseños modernos, desde postales y tarjetas de crédito hasta carteles y placas de interruptores de luz.
Stakhov, Alexey P. ; Olsen, Scott (2009). "§1.4.1 Un rectángulo áureo con una razón de lado de τ". Las matemáticas de la armonía: desde Euclides hasta las matemáticas y la informática contemporáneas . World Scientific. págs. 20-21.
Una tarjeta de crédito tiene la forma de un rectángulo áureo .
Cox, Simon (2004). Descifrando el Código Da Vinci. Barnes & Noble. pág. 62. ISBN 978-1-84317-103-4La proporción áurea también
aparece en algunos lugares muy inesperados: los televisores de pantalla ancha, las postales, las tarjetas de crédito y las fotografías suelen ajustarse a sus proporciones.
- ^ Posamentier & Lehmann 2011, capítulo 4, nota al pie 12: "La bandera de Togo fue diseñada por el artista Paul Ahyi (1930-2010), quien afirma haber intentado construir la bandera con la forma de un rectángulo dorado".
- ^ Lendvai, Ernő (1971). Béla Bartók: un análisis de su música . Londres: Kahn y Averill.
- ^ Livio 2002, pág. 190.
- ^ Smith, Peter F. (2003). La dinámica del deleite: arquitectura y estética. Routledge. pág. 83. ISBN 9780415300100.
- ^ Howat, Roy (1983). "1. Estructura proporcional y la sección áurea". Debussy en proporción: un análisis musical . Cambridge University Press. págs. 1–10.
- ^ Trezise, Simon (1994). Debussy: La Mer. Cambridge University Press. pág. 53. ISBN 9780521446563.
- ↑ Mongoven, Casey (2010). "Un estilo de música caracterizado por Fibonacci y la proporción áurea" (PDF) . Congressus Numerantium . 201 : 127–138.
Hasegawa, Robert (2011). " Gegenstrebige Harmonik en la música de Hans Zender". Perspectivas de la nueva música . 49 (1). Proyecto Muse: 207–234. doi :10.1353/pnm.2011.0000. JSTOR 10.7757/persnewmusi.49.1.0207.
Smethurst, Reilly (2016). "Dos afinaciones sin octava de Heinz Bohlen: una propuesta práctica". En Torrence, Eve; et al. (eds.). Actas de Bridges 2016. Jyväskylä, Finlandia. Tessellations Publishing. págs. 519–522.
- ^ Livio 2002, pág. 154.
- ^ Padovan, Richard (1999). Proporción: ciencia, filosofía, arquitectura . Taylor & Francis. págs. 305-306. doi :10.4324/9780203477465. ISBN . 9781135811112.
Padovan, Richard (2002). "Proporción: ciencia, filosofía, arquitectura". Nexus Network Journal . 4 (1): 113–122. doi : 10.1007/s00004-001-0008-7 .
- ^ Zeising, Adolf (1854). "Einleitung [prefacio]". Neue Lehre von den Proportionen des menschlichen Körpers [ Nueva doctrina de las proporciones del cuerpo humano ] (en alemán). Weigel. págs. 1–10.
- ^ Pommersheim, James E.; Marks, Tim K.; Flapan, Erica L. , eds. (2010). Teoría de números: una introducción animada con pruebas, aplicaciones e historias . Wiley. pág. 82.
- ^ Coldea, R.; Tennant, DA; Wheeler, EM; Wawrzynksa, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P.; Keifer, K. (2010). "Criticidad cuántica en una cadena de Ising: evidencia experimental de simetría E8 emergente". Science . 327 (5962): 177–180. arXiv : 1103.3694 . Bibcode :2010Sci...327..177C. doi :10.1126/science.1180085. PMID 20056884. S2CID 206522808.
- ^ "Una bola de discoteca en el espacio". NASA. 2001-10-09. Archivado desde el original el 2020-12-22 . Consultado el 2007-04-16 .
- ^ Faisán, Stephen (1986). Bodyspace . Taylor & Francis. ISBN. 9780850663402.
- ^ van Laack, Walter (2001). Una historia mejor de nuestro mundo: Volumen 1 El universo . Aquisgrán: van Laach.
- ^ Dunlap, Richard A. (1997). La proporción áurea y los números de Fibonacci . World Scientific. pág. 130.
- ^ Falbo, Clement (marzo de 2005). "La proporción áurea: un punto de vista contrario". The College Mathematics Journal . 36 (2): 123–134. doi :10.1080/07468342.2005.11922119. S2CID 14816926.
- ^ Moscovich, Ivan (2004). El cuadrado con bisagras y otros rompecabezas. Nueva York: Sterling. p. 122. ISBN 9781402716669.
- ^ Peterson, Ivars (1 de abril de 2005). «Espirales de conchas marinas». Science News . Archivado desde el original el 3 de octubre de 2012. Consultado el 10 de noviembre de 2008 .
- ^ Man, John (2002). Gutenberg: cómo un hombre rehizo el mundo con la palabra. Wiley. págs. 166-167. ISBN 9780471218234La página de medio folio (30,7 ×
44,5 cm) estaba formada por dos rectángulos (la página entera y su área de texto) basándose en la llamada "sección áurea", que especifica una relación crucial entre los lados corto y largo, y produce un número irracional, como lo es pi, pero es una proporción de aproximadamente 5:8.
- ^ Fechner, Gustav (1876). Vorschule der Ästhetik [ Preescolar de Estética ] (en alemán). Leipzig: Breitkopf & Härtel. págs. 190-202.
- ^ Livio 2002, pág. 7.
- ^ Osler, Carol (2000). "Support for Resistance: Technical Analysis and Intraday Exchange Rates" (PDF) . Revista de política económica del Banco de la Reserva Federal de Nueva York . 6 (2): 53–68. Archivado (PDF) desde el original el 12 de mayo de 2007.
Los retrocesos del 38,2 por ciento y el 61,8 por ciento de las subidas o bajadas recientes son comunes.
- ^ Batchelor, Roy ; Ramyar, Richard (2005). Números mágicos en el Dow (Informe). Cass Business School. págs. 13, 31.Se pueden encontrar resúmenes de prensa populares en: Stevenson, Tom (10 de abril de 2006). "Desde los tiempos en que 'lo grande es hermoso', los gigantes nunca habían tenido mejor aspecto". The Daily Telegraph ."Fallo técnico". The Economist . 23 de septiembre de 2006.
- ^ Herz-Fischler, Roger (2000). La forma de la Gran Pirámide . Wilfrid Laurier University Press. ISBN 0-88920-324-5.En todo el libro se examinan muchas teorías alternativas sobre la forma de esta pirámide. Véase el capítulo 11, "Teoría del triángulo de Kepler", págs. 80-91, para material específico sobre el triángulo de Kepler, y la pág. 166 para la conclusión de que la teoría del triángulo de Kepler puede eliminarse mediante el principio de que "Una teoría debe corresponder a un nivel de matemáticas consistente con lo que sabían los antiguos egipcios". Véase la nota 3, pág. 229, para la historia del trabajo de Kepler con este triángulo.
Rossi, Corinna (2004). Arquitectura y matemáticas en el Antiguo Egipto. Cambridge University Press. pp. 67–68.
No hay evidencia directa en ninguna fuente matemática escrita del Antiguo Egipto de ningún cálculo aritmético o construcción geométrica que pueda clasificarse como la Sección Áurea... convergencia a , y en sí misma como un número, no encajan con las fuentes matemáticas existentes del Reino Medio.
; véase también un extenso análisis de múltiples teorías alternativas sobre la forma de la pirámide y otras arquitecturas egipcias, págs. 7-56Rossi, Corinna; Tout, Christopher A. (2002). "¿Se conocían la serie de Fibonacci y la sección áurea en el antiguo Egipto?". Historia Mathematica . 29 (2): 101–113. doi :10.1006/hmat.2001.2334. hdl : 11311/997099 .
Markowsky, George (1992). "Misconceptions about the Golden Ratio" (PDF) . The College Mathematics Journal . 23 (1). Mathematical Association of America: 2–19. doi :10.2307/2686193. JSTOR 2686193 . Consultado el 29 de junio de 2012 .
No parece que los egipcios supieran siquiera de la existencia de y mucho menos que lo incorporaran en sus edificios .
- ^ Livio 2002, págs. 74–75.
- ^ Van Mersbergen, Audrey M. (1998). "Prototipos retóricos en arquitectura: medir la Acrópolis con una polémica filosófica". Communication Quarterly . 46 (2): 194–213. doi :10.1080/01463379809370095.
- ^ Devlin, Keith J. (2005). El instinto matemático. Nueva York: Thunder's Mouth Press. pág. 108.
- ^ Gazalé, Midhat J. (1999). Gnomon: de faraones a fractales . Princeton. pag. 125.ISBN 9780691005140.
- ^ Foutakis, Patrice (2014). "¿Construyeron los griegos según la proporción áurea?". Cambridge Archaeological Journal . 24 (1): 71–86. doi :10.1017/S0959774314000201. S2CID 162767334.
- ^ Le Salon de la Sección de Oro, octubre de 1912, Centro de Mediación Pompidou
- ^ Jeunes Peintres ne vous frappez pas!, La Sección de Oro: Numéro spécial consacré à l'Exposition de la "Section d'Or", estreno anual, núm. 1, 9 de octubre de 1912, págs. 1 a 7 Archivado el 30 de octubre de 2020 en Wayback Machine , Bibliothèque Kandinsky
- ^ Herz-Fischler, Roger (1983). "Un examen de las afirmaciones relativas a Seurat y el número áureo" (PDF) . Gazette des Beaux-Arts . 101 : 109–112.
- ^ Herbert, Robert (1968). Neoimpresionismo . Fundación Guggenheim. pág. 24.
- ^ Livio 2002, pág. 169.
- ^ ab Camfield, William A. (marzo de 1965). "Juan Gris y la sección áurea". The Art Bulletin . 47 (1): 128–134. doi :10.1080/00043079.1965.10788819.
- ^ Green, Christopher (1992). Juan Gris . Yale. Págs. 37-38. ISBN. 9780300053746.
Cottington, David (2004). Cubismo y sus historias. Manchester University Press. págs. 112, 142.
- ^ Allard, Roger (junio de 1911). "Sur quelques pintores". Les Marches du Sud-Ouest : 57–64.Reimpreso en Antliff, Mark; Leighten, Patricia, eds. (2008). Un lector de cubismo, documentos y crítica, 1906-1914. The University of Chicago Press. págs. 178-191.
- ^ Bouleau, Charles (1963). La geometría secreta del pintor: un estudio de la composición en el arte. Harcourt, Brace & World. págs. 247–248.
- ^ Livio 2002, págs. 177-178.
Obras citadas
- Herz-Fischler, Roger (1998) [1987]. Una historia matemática del número áureo . Dover. ISBN 9780486400075.(Título original: Una historia matemática de la división en razones extremas y medias ).
- Livio, Mario (2002). La proporción áurea: la historia de Phi, el número más asombroso del mundo . Nueva York: Broadway Books. ISBN 9780767908153.
- Posamentier, Alfred S. ; Lehmann, Ingmar (2011). La gloriosa proporción áurea. Prometheus Books . ISBN 9-781-61614-424-1.
Lectura adicional
- Doczi, György (1981). El poder de los límites: armonías proporcionales en la naturaleza, el arte y la arquitectura . Boston: Shambhala.
- Hargittai, István, ed. (1992). Quíntuple Simetría . Científico mundial. ISBN 9789810206000.
- Huntley, HE (1970). La divina proporción: un estudio sobre la belleza matemática . Nueva York: Dover. ISBN 978-0-486-22254-7.
- Schaaf, William L., ed. (1967). The Golden Measure (PDF) . Serie de reimpresiones del California School Mathematics Study Group. Universidad de Stanford. Archivado (PDF) desde el original el 25 de abril de 2015.
- Scimone, Aldo (1997). La Sección Áurea. Historia cultural de un leitmotiv della Matematica . Palermo: Sigma Edizioni. ISBN 978-88-7231-025-0.
- Walser, Hans (2001) [ Der Goldene Schnitt 1993]. La Sección Dorada . Peter Hilton trad. Washington, DC: Asociación Matemática de América. ISBN 978-0-88385-534-8.
Enlaces externos
- Weisstein, Eric W. "Proporción áurea". MundoMatemático .
- Bogomolny, Alexander (2018). "Proporción áurea en geometría". Cut-the-Knot .
- Knott, Ron. "La proporción áurea: Phi".Información y actividades de un profesor de matemáticas.
- El mito que no desaparecerá Archivado el 12 de noviembre de 2020 en Wayback Machine , por Keith Devlin , que aborda múltiples acusaciones sobre el uso de la proporción áurea en la cultura.
- Espirales doradas espurias recopiladas por Randall Munroe
- Conferencia en YouTube sobre el problema de los ratones de Zenón y las espirales logarítmicas








































![{\displaystyle {\begin{aligned}\varphi ^{2}&=\varphi +1=2.618033\dots ,\\[5mu]{\frac {1}{\varphi }}&=\varphi -1=0.618033 \puntos .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff2e5225abf67548cf93c882add3a4b439c4aeb8)






![{\displaystyle {\begin{aligned}\varphi ^{n}&=\varphi ^{n-1}+\varphi ^{n-3}+\cdots +\varphi ^{n-1-2m}+\ varphi ^{n-2-2m}\\[5mu]\varphi ^{n}-\varphi ^{n-1}&=\varphi ^{n-2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/048f09b7012c7fbd3d9f32798de6dd5c01acabcd)

![{\displaystyle \varphi =[1;1,1,1,\puntos ]=1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{{\vphantom {1}} \atop \ddots }}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b68e302b5301938b37b40e527a07c83a1f58e830)
![{\displaystyle \varphi ^{-1}=[0;1,1,1,\puntos ]=0+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{{\vphantom {1}} \atop \ddots }}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/224ea872a3a53d5fbe1ab6d1a9a67c37e5320bed)

















































![{\displaystyle {\begin{aligned}&{\bigl \vert }L_{n}-{\sqrt {5}}F_{n}{\bigr \vert }={\frac {2}{\varphi ^{n}}}\to 0,\\[5mu]&{\bigl (}{\tfrac {1}{2}}L_{3n}{\bigr )}^{2}=5{\bigl (}{\tfrac {1}{2}}F_{3n}{\bigr )}^{2}+(-1)^{n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b76ec76fed5b0692ae8e9be070b4c2d620aa69ef)



![{\displaystyle {\begin{aligned}3\varphi ^{3}-5\varphi ^{2}+4&=3(\varphi ^{2}+\varphi )-5\varphi ^{2}+4\ \[5mu]&=3{\bigl (}(\varphi +1)+\varphi {\bigr )}-5(\varphi +1)+4\\[5mu]&=\varphi +2\aproximadamente 3,618033.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9eba46117303993ef0998e4dc1c99ef34e511a00)


![{\displaystyle {\begin{aligned}\varphi ^{0}&=1,\\[5mu]\varphi ^{1}&=1,618033989\ldots \aprox 2,\\[5mu]\varphi ^{2}&=2,618033989\ldots \aprox 3,\\[5mu]\varphi ^{3}&=4,236067978\ldots \aprox 4,\\[5mu]\varphi ^{4}&=6,854101967\ldots \aprox 7,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4ac9ddf7e52ee6d1d0976b18e49ea4a99375dee)



















![{\displaystyle {\begin{alineado}{\frac {2\pi -g}{g}}&={\frac {2\pi }{2\pi -g}}=\varphi ,\\[8mu] 2\pi -g&={\frac {2\pi }{\varphi }}\aprox 222.5^{\circ }\!,\\[8mu]g&={\frac {2\pi }{\varphi ^{2}}}\aprox 137,5^{\circ }\!.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40b2a5dd8ad7ae0f2e1c53bb43bb82e62d85e348)



![{\displaystyle {\begin{aligned}\varphi &=1+2\sin(\pi /10)=1+2\sin 18^{\circ }\!,\\[5mu]\varphi &={\ tfrac {1}{2}}\csc(\pi /10)={\tfrac {1}{2}}\csc 18^{\circ }\!,\\[5mu]\varphi &=2\cos(\pi /5)=2\cos 36^{\circ }\!,\\[5mu]\varphi &=2\sin(3\pi /10)=2\sin 54^{ \circ }\!.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a0a8da53781e6f8e49ac9f4d5b9331a3ddf4dbf)













![{\displaystyle {\begin{aligned}A&={\tfrac {1}{2}}s^{2}{\sqrt {\varphi {\vphantom {+}}}},\\[5mu]\theta &=\sin ^{-1}{\frac {1}{\varphi }}\approx 38,1727^{\circ }\!,\\[5mu]\theta &=\cos ^{-1}{\frac {1}{\varphi }}\approx 51,8273^{\circ }\!.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/779f1f91238ee7d20831ce7a01708467f451686d)
![{\displaystyle {\begin{aligned}\alpha &=2\arctan {1 \sobre \varphi }\aproximadamente 63,43495^{\circ }\!,\\[5mu]\beta &=2\arctan \varphi =\pi -\arctan 2=\arctan 1+\arctan 3\aproximadamente 116,56505^{\circ }\!.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c119812addb94dc1e424cadd77557bd18fd278ce)

![{\displaystyle {\begin{aligned}d&={\frac {2a}{\sqrt {2+\varphi }}}=2{\sqrt {\frac {3-\varphi }{5}}}a\aproximadamente 1,05146a,\\[5mu]D&=2{\sqrt {\frac {2+\varphi }{5}}}a\aproximadamente 1,70130a.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e065f9b4f3ea5c64f0201b0a37108b249b2b7e0)
![{\displaystyle {\begin{aligned}A&=\sin(\arctan 2)\cdot a^{2}={2 \sobre {\sqrt {5}}}~a^{2}\aproximadamente 0,89443a^{2},\\[5mu]A&={{\varphi } \sobre 2}d^{2}\aproximadamente 0,80902d^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/046e7158ac6208efb25197529492b0151b305d72)




































![{\displaystyle \mathbb {Z} [\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f984c2710477c64fca0f16a71928134bdb8201)
![{\displaystyle {\begin{aligned}e^{0}+e^{-0}&=2,\\[5mu]e^{2\pi i/5}+e^{-2\pi i/ 5}&=\varphi ^{-1}=-1+\varphi ,\\[5mu]e^{4\pi i/5}+e^{-4\pi i/5}&=-\varphi .\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec7bcbd2e99aef0874eb163966c3e2dd9424b86)

![{\displaystyle {\begin{aligned}e^{\pi i}+e^{-\pi i}&=-2,\\[5mu]e^{\pi i/5}+e^{-\ pi i/5}&=\varphi ,\\[5mu]e^{3\pi i/5}+e^{-3\pi i/5}&=-\varphi ^{-1}=1- \varphi .\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9459634b32b6990a97eb560ce696a3bc2e722513)

















![{\displaystyle {\begin{aligned}{\Bigl (}\varphi +R{{\bigl (}e^{-2a}{\bigr )}}{\Bigr )}{\Bigl (}\varphi +R {{\bigl (}e^{-2b}{\bigr )}}{\Bigr )}&=\varphi {\sqrt {5}},\\[5mu]{\Bigl (}\varphi ^{-1}-R{{\bigl (}{-e^{-a}}{\bigr )}}{\Bigr )}{\Bigl (}\varphi ^{-1}-R{{\ bigl (}{-e^{-b}}{\bigr )}}{\Bigr )}&=\varphi ^{-1}{\sqrt {5}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efa72855991c37845330a894d36b1d91647a265a)





















