Metamaterial de índice negativo

El metamaterial de índice negativo o material de índice negativo ( NIM ) es un metamaterial cuyo índice de refracción para una onda electromagnética tiene un valor negativo en un rango de frecuencia determinado . ^[1]

Los NIM están construidos a partir de partes básicas periódicas llamadas celdas unitarias , que suelen ser significativamente más pequeñas que la longitud de onda de la radiación electromagnética aplicada externamente . Las celdas unitarias de los primeros NIM investigados experimentalmente se construyeron a partir de material de placa de circuito , o en otras palabras, cables y dieléctricos . En general, estas celdas construidas artificialmente están apiladas o son planas y configuradas en un patrón repetido particular para componer el NIM individual. Por ejemplo, las celdas unitarias de los primeros NIM se apilaron horizontal y verticalmente, lo que dio como resultado un patrón que se repitió y se intencionó (ver imágenes a continuación).

Las especificaciones para la respuesta de cada celda unitaria se determinan previamente antes de la construcción y se basan en la respuesta prevista de todo el material recién construido. En otras palabras, cada celda se ajusta individualmente para responder de una determinada manera, en función del resultado deseado del NIM. La respuesta agregada está determinada principalmente por la geometría de cada celda unitaria y difiere sustancialmente de la respuesta de sus materiales constituyentes. En otras palabras, la forma en que responde el NIM es la de un nuevo material, a diferencia de los cables o metales y dieléctricos de los que está hecho. Por lo tanto, el NIM se ha convertido en un medio eficaz . Además, en efecto, este metamaterial se ha convertido en un " material macroscópico ordenado , sintetizado de abajo hacia arriba", y tiene propiedades emergentes más allá de sus componentes. ^[2]

Los metamateriales que presentan un valor negativo para el índice de refracción a menudo se denominan con alguna de varias terminologías: medios zurdos o material zurdo (LHM), medios de onda retrógrada (medios BW), medios con índice de refracción negativo, metamateriales doblemente negativos (DNG) y otros nombres similares. ^[3]

La electrodinámica de los medios con índices de refracción negativos fue estudiada por primera vez por el físico teórico ruso Victor Veselago del Instituto de Física y Tecnología de Moscú en 1967. ^{[6] Se} teorizó que los materiales levógiros o de índice negativo propuestos exhibirían propiedades ópticas opuestas a las del vidrio , el aire y otros medios transparentes . Se predijo que dichos materiales exhibirían propiedades contraintuitivas como doblar o refractar la luz de formas inusuales e inesperadas. Sin embargo, el primer metamaterial práctico no se construyó hasta 33 años después y sí respalda los conceptos de Veselago. ^{[1] [3] [6] [7]}

En la actualidad, se están desarrollando metamateriales de índice negativo para manipular la radiación electromagnética de nuevas maneras. Por ejemplo, las propiedades ópticas y electromagnéticas de los materiales naturales suelen alterarse mediante la química . Con los metamateriales, las propiedades ópticas y electromagnéticas se pueden diseñar modificando la geometría de sus celdas unitarias . Las celdas unitarias son materiales que están ordenados en disposiciones geométricas con dimensiones que son fracciones de la longitud de onda de la onda electromagnética radiada . Cada unidad artificial responde a la radiación de la fuente. El resultado colectivo es la respuesta del material a la onda electromagnética que es más amplia de lo normal. ^{[1] [3] [7]}

Posteriormente, la transmisión se altera ajustando la forma, el tamaño y las configuraciones de las celdas unitarias. Esto da como resultado el control sobre los parámetros del material conocidos como permitividad y permeabilidad magnética . Estos dos parámetros (o cantidades) determinan la propagación de las ondas electromagnéticas en la materia . Por lo tanto, controlar los valores de permitividad y permeabilidad significa que el índice de refracción puede ser negativo o cero, así como convencionalmente positivo. Todo depende de la aplicación prevista o el resultado deseado . Por lo tanto, las propiedades ópticas se pueden expandir más allá de las capacidades de las lentes , espejos y otros materiales convencionales. Además, uno de los efectos más estudiados es el índice de refracción negativo. ^{[1] [3] [6] [7]}

Cuando se produce un índice de refracción negativo, la propagación de la onda electromagnética se invierte. Se hace posible una resolución por debajo del límite de difracción . Esto se conoce como imágenes de sublongitud de onda . La transmisión de un haz de luz a través de una superficie electromagnéticamente plana es otra capacidad. En cambio, los materiales convencionales suelen ser curvos y no pueden lograr una resolución por debajo del límite de difracción. Además, la inversión de las ondas electromagnéticas en un material, junto con otros materiales ordinarios (incluido el aire), podría dar como resultado la minimización de las pérdidas que se producirían normalmente. ^{[1] [3] [6] [7]}

La onda electromagnética inversa, caracterizada por una velocidad de fase antiparalela , también es un indicador de índice de refracción negativo. ^{[1] [6]}

Además, los materiales de índice negativo son compuestos personalizados. En otras palabras, los materiales se combinan con un resultado deseado en mente. Se pueden diseñar combinaciones de materiales para lograr propiedades ópticas que no se ven en la naturaleza. Las propiedades del material compuesto se derivan de su estructura reticular construida a partir de componentes más pequeños que la longitud de onda electromagnética incidente separados por distancias que también son más pequeñas que la longitud de onda electromagnética incidente. Asimismo, al fabricar dichos metamateriales, los investigadores están tratando de superar los límites fundamentales vinculados a la longitud de onda de la luz . ^{[1] [3] [7]} Las propiedades inusuales y contraintuitivas actualmente tienen un uso práctico y comercial en la manipulación de microondas electromagnéticas en sistemas inalámbricos y de comunicación . Por último, la investigación continúa en los otros dominios del espectro electromagnético , incluida la luz visible . ^{[7] [8]}

Los primeros metamateriales reales funcionaron en el régimen de microondas , o longitudes de onda centimétricas , del espectro electromagnético (alrededor de 4,3 GHz). Se construyeron con resonadores de anillo dividido y cables rectos conductores (como celdas unitarias). Las celdas unitarias tenían un tamaño de 7 a 10 milímetros . Las celdas unitarias estaban dispuestas en un patrón repetitivo bidimensional ( periódico ) que produce una geometría similar a la de un cristal . Tanto las celdas unitarias como el espaciado reticular eran más pequeños que la onda electromagnética radiada. Esto produjo el primer material levógiro cuando tanto la permitividad como la permeabilidad del material eran negativas. Este sistema se basa en el comportamiento resonante de las celdas unitarias. A continuación, un grupo de investigadores desarrolla una idea para un metamaterial levógiro que no depende de dicho comportamiento resonante.

La investigación en el rango de microondas continúa con resonadores de anillo dividido y cables conductores. La investigación también continúa en las longitudes de onda más cortas con esta configuración de materiales y los tamaños de celdas unitarias se reducen. Sin embargo, alrededor de los 200 terahercios surgen problemas que hacen que el uso del resonador de anillo dividido sea problemático. " Los materiales alternativos se vuelven más adecuados para los regímenes ópticos y de terahercios ". En estas longitudes de onda, la selección de materiales y las limitaciones de tamaño se vuelven importantes. ^{[1] [4] [9] [10]} Por ejemplo, en 2007 un diseño de alambre de malla de 100 nanómetros hecho de plata y tejido en un patrón repetitivo transmitió haces en la longitud de onda de 780 nanómetros, el extremo más alejado del espectro visible. Los investigadores creen que esto produjo una refracción negativa de 0,6. Sin embargo, esto opera solo en una única longitud de onda como sus metamateriales predecesores en el régimen de microondas. Por lo tanto, los desafíos son fabricar metamateriales de manera que "refracten la luz en longitudes de onda cada vez más pequeñas" y desarrollar capacidades de banda ancha. ^{[11] [12]}

En la literatura sobre metamateriales , el término medio o medio se refiere a un medio de transmisión o medio óptico . En 2002, un grupo de investigadores ideó la idea de que, a diferencia de los materiales que dependían del comportamiento resonante, los fenómenos no resonantes podían superar las limitaciones de ancho de banda estrecho de la configuración del resonador de anillo dividido/alambre . Esta idea se tradujo en un tipo de medio con capacidades de ancho de banda más amplio, refracción negativa , ondas hacia atrás y enfoque más allá del límite de difracción .

Previnieron los resonadores de anillo dividido y en su lugar utilizaron una red de líneas de transmisión cargadas L–C . En la literatura metamaterial esto se conoció como medio de línea de transmisión artificial . En ese momento tenía la ventaja adicional de ser más compacto que una unidad hecha de cables y resonadores de anillo dividido. La red era escalable (desde el rango de megahercios hasta las decenas de gigahercios ) y ajustable. También incluye un método para enfocar las longitudes de onda de interés . ^[13] En 2007, la línea de transmisión de índice de refracción negativo se empleó como una lente plana de espacio libre de enfoque de sublongitud de onda. Que se trate de una lente de espacio libre es un avance significativo. Parte de los esfuerzos de investigación anteriores apuntaron a crear una lente que no necesitara estar incrustada en una línea de transmisión. ^[14]

Los componentes metamateriales se reducen a medida que la investigación explora longitudes de onda más cortas (frecuencias más altas) del espectro electromagnético en los espectros infrarrojo y visible . Por ejemplo, la teoría y la experimentación han investigado resonadores de anillo dividido en forma de herradura más pequeños diseñados con técnicas litográficas , ^{[15] [16]} así como nanobarras o nanotiras de metal emparejadas, ^[17] y nanopartículas como circuitos diseñados con modelos de elementos concentrados ^[18]

La ciencia de los materiales de índice negativo se está combinando con dispositivos convencionales que emiten, transmiten, dan forma o reciben señales electromagnéticas que viajan a través de cables, alambres o aire. Los materiales, dispositivos y sistemas que están involucrados en este trabajo podrían tener sus propiedades alteradas o aumentadas. Por lo tanto, esto ya está sucediendo con antenas metamateriales ^[19] y dispositivos relacionados que están disponibles comercialmente. Además, en el dominio inalámbrico estos aparatos metamateriales continúan siendo investigados. También se están investigando otras aplicaciones. Estas son absorbentes electromagnéticos como absorbentes de microondas de radar , resonadores eléctricamente pequeños , guías de ondas que pueden ir más allá del límite de difracción , compensadores de fase , avances en dispositivos de enfoque (por ejemplo, lentes de microondas ) y antenas eléctricamente pequeñas mejoradas. ^{[20] [21] [22] [23]}

En el régimen de frecuencia óptica , el desarrollo de superlentes puede permitir la obtención de imágenes por debajo del límite de difracción . Otras aplicaciones potenciales para los metamateriales de índice negativo son la nanolitografía óptica , los circuitos nanotecnológicos , así como una superlente de campo cercano (Pendry, 2000) que podría ser útil para la obtención de imágenes biomédicas y la fotolitografía de longitud de onda inferior. ^[23]

Para describir las propiedades electromagnéticas de un material aquiral dado, como una lente óptica , hay dos parámetros importantes: la permitividad , y la permeabilidad , que permiten predecir con precisión las ondas de luz que viajan dentro de los materiales y los fenómenos electromagnéticos que ocurren en la interfaz entre dos materiales. ^[24]$estilo de visualización {\epsilon_{r}}$${\displaystyle \mu_{r}}$

Por ejemplo, la refracción es un fenómeno electromagnético que ocurre en la interfaz entre dos materiales. La ley de Snell establece que la relación entre el ángulo de incidencia de un haz de radiación electromagnética (luz) y el ángulo de refracción resultante se basa en los índices de refracción, , de los dos medios (materiales). El índice de refracción de un medio aquiral está dado por . ^[25] Por lo tanto, se puede ver que el índice de refracción depende de estos dos parámetros. Por lo tanto, si se pueden introducir valores diseñados o modificados arbitrariamente para y , entonces se puede manipular a voluntad el comportamiento de propagación de las ondas electromagnéticas dentro del material. Esta capacidad permite entonces la determinación intencional del índice de refracción. ^[24]${\estilo de visualización n}$${\displaystyle \scriptstyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}}}$$estilo de visualización {\epsilon_{r}}$${\displaystyle \mu_{r}}$

Por ejemplo, en 1967, Victor Veselago determinó analíticamente que la luz se refractará en la dirección inversa (negativamente) en la interfaz entre un material con índice de refracción negativo y un material que exhibe un índice de refracción positivo convencional . Este extraordinario material fue realizado en papel con valores negativos simultáneos para y , y por lo tanto podría denominarse un material doblemente negativo. Sin embargo, en la época de Veselago un material que exhiba parámetros doblemente negativos simultáneamente parecía imposible porque no existen materiales naturales que puedan producir este efecto. Por lo tanto, su trabajo fue ignorado durante tres décadas. ^[24] Fue nominado para el Premio Nobel más tarde. $estilo de visualización {\epsilon_{r}}$${\displaystyle \mu_{r}}$

En general, las propiedades físicas de los materiales naturales causan limitaciones. La mayoría de los dieléctricos solo tienen permitividades positivas, > 0. Los metales exhibirán permitividad negativa, < 0 en frecuencias ópticas, y los plasmas exhiben valores de permitividad negativos en ciertas bandas de frecuencia. Pendry et al. demostraron que la frecuencia del plasma se puede hacer que ocurra en las frecuencias de microondas más bajas para metales con un material hecho de varillas de metal que reemplaza el metal a granel . Sin embargo, en cada uno de estos casos, la permeabilidad permanece siempre positiva. En frecuencias de microondas es posible que se produzcan μ negativos en algunos materiales ferromagnéticos . Pero el inconveniente inherente es que son difíciles de encontrar por encima de las frecuencias de terahercios . En cualquier caso, no se ha encontrado ni descubierto un material natural que pueda lograr valores negativos de permitividad y permeabilidad simultáneamente. Por lo tanto, todo esto ha llevado a construir materiales compuestos artificiales conocidos como metamateriales para lograr los resultados deseados. ^[24]$estilo de visualización {\epsilon_{r}}$$estilo de visualización {\epsilon_{r}}$

En el caso de materiales quirales , el índice de refracción depende no solo de la permitividad y la permeabilidad , sino también del parámetro de quiralidad , lo que da como resultado valores distintos para ondas polarizadas circularmente izquierdas y derechas, dados por${\estilo de visualización n}$$estilo de visualización {\epsilon_{r}}$${\displaystyle \mu_{r}}$${\estilo de visualización \kappa}$

${\displaystyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}}\pm \kappa }$

Se producirá un índice negativo para ondas de una polarización circular si > . En este caso, no es necesario que uno o ambos y sean negativos para lograr un índice de refracción negativo. Un índice de refracción negativo debido a la quiralidad fue predicho por Pendry ^[26] y Tretyakov et al. , ^[27] y observado por primera vez de manera simultánea e independiente por Plum et al. ^[28] y Zhang et al. ^[29] en 2009.${\estilo de visualización \kappa}$${\displaystyle {\sqrt {\epsilon _{r}\mu _{r}}}}$$estilo de visualización {\epsilon_{r}}$${\displaystyle \mu_{r}}$

En 1996 y 1999 se publicaron artículos teóricos que demostraban que se podían construir materiales sintéticos que exhibieran deliberadamente una permitividad y permeabilidad negativas . ^{[nota 1]}

Estos artículos, junto con el análisis teórico de Veselago de 1967 sobre las propiedades de los materiales de índice negativo, proporcionaron la base para fabricar un metamaterial con permitividad y permeabilidad efectivas negativas. ^{[30] [31] [32]} Véase más abajo.

Un metamaterial desarrollado para exhibir un comportamiento de índice negativo se forma típicamente a partir de componentes individuales. Cada componente responde de manera diferente e independiente a una onda electromagnética radiada a medida que viaja a través del material. Dado que estos componentes son más pequeños que la longitud de onda radiada , se entiende que una visión macroscópica incluye un valor efectivo tanto para la permitividad como para la permeabilidad. ^[30]

En el año 2000, el equipo de investigadores de la UCSD dirigido por David R. Smith produjo una nueva clase de materiales compuestos depositando una estructura sobre un sustrato de placa de circuito que consistía en una serie de anillos delgados de cobre partidos y segmentos de alambre ordinarios tendidos en paralelo a los anillos. Este material exhibía propiedades físicas inusuales que nunca se habían observado en la naturaleza. Estos materiales obedecen las leyes de la física , pero se comportan de manera diferente a los materiales normales. En esencia, estos metamateriales de índice negativo se destacaron por tener la capacidad de revertir muchas de las propiedades físicas que gobiernan el comportamiento de los materiales ópticos ordinarios. Una de esas propiedades inusuales es la capacidad de revertir, por primera vez, la ley de refracción de Snell . Hasta que el equipo de la UCSD demostró el índice de refracción negativo para las microondas, el material no había estado disponible. Los avances durante la década de 1990 en las capacidades de fabricación y computación permitieron que se construyeran estos primeros metamateriales . De este modo, el "nuevo" metamaterial fue probado para los efectos descritos por Victor Veselago 30 años antes. Los estudios de este experimento, que se realizaron poco después, anunciaron que se habían producido otros efectos. ^{[5] [30] [31] [33]}

Con antiferroimanes y ciertos tipos de ferroimanes aislantes , se puede lograr una permeabilidad magnética negativa efectiva cuando existe resonancia de polaritones . Sin embargo, para lograr un índice de refracción negativo, debe darse una permitividad con valores negativos dentro del mismo rango de frecuencia. El resonador de anillo dividido fabricado artificialmente es un diseño que logra esto, junto con la promesa de amortiguar las altas pérdidas. Con esta primera introducción del metamaterial, parece que las pérdidas incurridas fueron menores que las de los materiales antiferromagnéticos o ferromagnéticos. ^[5]

Cuando se demostró por primera vez en 2000, el material compuesto (NIM) estaba limitado a transmitir radiación de microondas a frecuencias de 4 a 7 gigahercios (longitudes de onda de 4,28 a 7,49 cm). Este rango está entre la frecuencia de los hornos microondas domésticos ( ~2,45  GHz , 12,23 cm) y los radares militares (~10 GHz, 3 cm). En las frecuencias demostradas, los pulsos de radiación electromagnética que se mueven a través del material en una dirección están compuestos de ondas constituyentes que se mueven en la dirección opuesta. ^{[5] [33] [34]}

El metamaterial se construyó como una matriz periódica de elementos conductores de cobre en forma de anillo dividido y alambre depositados sobre un sustrato de placa de circuito. El diseño fue tal que las celdas y el espaciado reticular entre las celdas eran mucho más pequeños que la longitud de onda electromagnética radiada . Por lo tanto, se comporta como un medio efectivo . El material se ha vuelto notable porque su rango de valores de permitividad (efectiva) ε _eff y permeabilidad μ _eff han excedido los encontrados en cualquier material ordinario. Además, la característica de permeabilidad negativa (efectiva) evidenciada por este medio es particularmente notable, porque no se ha encontrado en materiales ordinarios. Además, los valores negativos para el componente magnético están directamente relacionados con su nomenclatura para zurdos y propiedades (discutidas en una sección a continuación). El resonador de anillo dividido (SRR), basado en el artículo teórico anterior de 1999, es la herramienta empleada para lograr permeabilidad negativa. Este primer metamaterial compuesto está entonces compuesto de resonadores de anillo dividido y postes conductores eléctricos. ^[5]

Inicialmente, estos materiales sólo se demostraron en longitudes de onda más largas que las del espectro visible . Además, los primeros NIM se fabricaron a partir de materiales opacos y generalmente estaban hechos de componentes no magnéticos. Sin embargo, a modo de ejemplo, si estos materiales se construyen en frecuencias visibles y se ilumina con una linterna la placa de NIM resultante, el material debería enfocar la luz en un punto del otro lado. Esto no es posible con una lámina de material opaco ordinario. ^{[1] [5] [33]} En 2007, el NIST en colaboración con el Laboratorio Atwater en Caltech creó el primer NIM activo en frecuencias ópticas. Más recientemente (a partir de 2008 ^[actualizar]), se han integrado materiales NIM en "red de pesca" en capas hechos de cables de silicio y plata en fibras ópticas para crear elementos ópticos activos. ^{[35] [36] [37]}

La permitividad negativa ε _eff < 0 ya se había descubierto y realizado en metales para frecuencias que llegaban hasta la frecuencia del plasma , antes del primer metamaterial. Hay dos requisitos para lograr un valor negativo para la refracción . En primer lugar, es fabricar un material que pueda producir una permeabilidad negativa μ _eff < 0. En segundo lugar, los valores negativos tanto para la permitividad como para la permeabilidad deben ocurrir simultáneamente en un rango común de frecuencias. ^{[1] [30]}

Por lo tanto, para el primer metamaterial, los elementos básicos son un resonador de anillo dividido combinado electromagnéticamente con un poste conductor (eléctrico). Estos están diseñados para resonar a frecuencias designadas para lograr los valores deseados. Al observar la composición del anillo dividido, el patrón de campo magnético asociado del SRR es dipolar . Este comportamiento dipolar es notable porque significa que imita el átomo de la naturaleza , pero a una escala mucho mayor, como en este caso a 2,5 milímetros . Los átomos existen en la escala de picómetros .

Las divisiones en los anillos crean una dinámica en la que la celda unitaria SRR puede hacerse resonante en longitudes de onda radiadas mucho mayores que el diámetro de los anillos. Si los anillos estuvieran cerrados, se impondría electromagnéticamente un límite de media longitud de onda como requisito para la resonancia . ^[5]

La división en el segundo anillo está orientada de manera opuesta a la división en el primer anillo. Está ahí para generar una gran capacitancia , que se produce en el pequeño espacio. Esta capacitancia disminuye sustancialmente la frecuencia de resonancia mientras concentra el campo eléctrico . El SRR individual representado a la derecha tenía una frecuencia de resonancia de 4,845 GHz , y también se muestra la curva de resonancia, insertada en el gráfico. Se observa que las pérdidas radiativas por absorción y reflexión son pequeñas, porque las dimensiones de la unidad son mucho más pequeñas que la longitud de onda radiada en el espacio libre . ^[5]

Cuando estas unidades o celdas se combinan en una disposición periódica , el acoplamiento magnético entre los resonadores se fortalece y se produce un fuerte acoplamiento magnético . Comienzan a surgir propiedades únicas en comparación con los materiales ordinarios o convencionales. Por un lado, este fuerte acoplamiento periódico crea un material que ahora tiene una permeabilidad magnética efectiva μ _eff en respuesta al campo magnético incidente radiado . ^[5]

Al graficar la curva de dispersión general , se produce una región de propagación desde cero hasta un borde de banda inferior , seguido de un espacio y luego una banda de paso superior . La presencia de un espacio de 400 MHz entre 4,2 GHz y 4,6 GHz implica una banda de frecuencias donde μ _eff < 0.

( Ver imagen en la sección anterior )

Además, cuando se añaden cables simétricamente entre los anillos divididos, se produce una banda de paso dentro de la banda previamente prohibida de las curvas de dispersión de los anillos divididos. El hecho de que esta banda de paso se produzca dentro de una región previamente prohibida indica que la ε _eff negativa para esta región se ha combinado con la μ _eff negativa para permitir la propagación, lo que se ajusta a las predicciones teóricas. Matemáticamente, la relación de dispersión conduce a una banda con velocidad de grupo negativa en todas partes y un ancho de banda que es independiente de la frecuencia del plasma , dentro de las condiciones establecidas. ^[5]

Tanto los modelos matemáticos como los experimentos han demostrado que los elementos conductores dispuestos periódicamente (no magnéticos por naturaleza) responden predominantemente al componente magnético de los campos electromagnéticos incidentes . El resultado es un medio efectivo y μ _eff negativo sobre una banda de frecuencias. Se verificó que la permeabilidad era la región de la banda prohibida, donde se produjo la brecha en la propagación, desde una sección finita de material. Esto se combinó con un material de permitividad negativa, ε _eff < 0, para formar un medio "zurdo", que formó una banda de propagación con velocidad de grupo negativa donde anteriormente solo había atenuación. Esto validó las predicciones. Además, un trabajo posterior determinó que este primer metamaterial tenía un rango de frecuencias sobre el cual se predijo que el índice de refracción sería negativo para una dirección de propagación (ver ref. # ^[1] ). Otros efectos electrodinámicos predichos se investigarían en otra investigación. ^[5]

A partir de las conclusiones de la sección anterior se puede definir un material zurdo (LHM). Es un material que exhibe valores negativos simultáneos para la permitividad , ε, y la permeabilidad , μ, en una región de frecuencia superpuesta. Dado que los valores se derivan de los efectos del sistema de medio compuesto en su conjunto, estos se definen como permitividad efectiva, ε _eff , y permeabilidad efectiva, μ _eff . Luego se derivan los valores reales para denotar el valor del índice de refracción negativo y los vectores de onda . Esto significa que en la práctica se producirán pérdidas para un medio dado utilizado para transmitir radiación electromagnética como, por ejemplo, microondas , o frecuencias infrarrojas , o luz visible . En este caso, los valores reales describen la amplitud o la intensidad de una onda transmitida en relación con una onda incidente, mientras que ignoran los valores de pérdida despreciables. ^{[4] [5]}

En las secciones anteriores, el primer metamaterial fabricado se construyó con elementos resonantes , que exhibieron una dirección de incidencia y polarización . En otras palabras, esta estructura exhibió propagación levógira en una dimensión. Esto se discutió en relación con el trabajo seminal de Veselago 33 años antes (1967). Predijo que intrínsecos a un material, que manifiesta valores negativos de permitividad y permeabilidad efectivas , hay varios tipos de fenómenos físicos inversos . Por lo tanto, había una necesidad crítica de un LHM de dimensiones superiores para confirmar la teoría de Veselago, como se esperaba. La confirmación incluiría la inversión de la ley de Snell (índice de refracción), junto con otros fenómenos inversos.

A principios de 2001 se informó de la existencia de una estructura de dimensiones superiores. Era bidimensional y se demostró tanto experimentalmente como mediante confirmación numérica. Se trataba de un LHM, un compuesto construido a partir de tiras de alambre montadas detrás de los resonadores de anillos partidos (SRR) en una configuración periódica. Se creó con el propósito expreso de ser adecuado para experimentos posteriores para producir los efectos predichos por Veselago. ^[4]

Un trabajo teórico publicado en 1967 por el físico soviético Victor Veselago demostró que es posible un índice de refracción con valores negativos y que esto no viola las leyes de la física. Como se discutió anteriormente (arriba), el primer metamaterial tenía un rango de frecuencias en el cual se predijo que el índice de refracción sería negativo para una dirección de propagación . Se informó en mayo de 2000. ^{[1] [6] [38]}

En 2001, un equipo de investigadores construyó un prisma compuesto de metamateriales (metamateriales de índice negativo) para probar experimentalmente el índice de refracción negativo. El experimento utilizó una guía de ondas para ayudar a transmitir la frecuencia adecuada y aislar el material. Esta prueba logró su objetivo porque verificó con éxito un índice de refracción negativo. ^{[1] [6] [39] [40] [41] [42] [43]}

La demostración experimental del índice de refracción negativo fue seguida por otra demostración, en 2003, de una inversión de la ley de Snell, o refracción inversa. Sin embargo, en este experimento el material con índice de refracción negativo se encuentra en el espacio libre entre 12,6 y 13,2 GHz. Aunque el rango de frecuencias radiadas es aproximadamente el mismo, una distinción notable es que este experimento se lleva a cabo en el espacio libre en lugar de emplear guías de ondas. ^[44]

Para reforzar la autenticidad de la refracción negativa, se calculó el flujo de potencia de una onda transmitida a través de un material dispersivo levógiro y se comparó con un material dispersivo levógiro. Se emplea la transmisión de un campo incidente, compuesto de muchas frecuencias, desde un material no dispersivo isótropo a un medio dispersivo isótropo. La dirección del flujo de potencia tanto para el medio dispersivo como para el no dispersivo se determina mediante el vector de Poynting promediado en el tiempo . Se demostró que la refracción negativa es posible para señales de frecuencia múltiple mediante el cálculo explícito del vector de Poynting en el LHM. ^[45]

En una placa de material convencional con un índice de refracción ordinario (un material dextrógiro, RHM), el frente de onda se transmite alejándose de la fuente. En un NIM, el frente de onda viaja hacia la fuente. Sin embargo, la magnitud y la dirección del flujo de energía permanecen esencialmente iguales tanto en el material ordinario como en el NIM. Dado que el flujo de energía permanece igual en ambos materiales (medios), la impedancia del NIM coincide con el RHM. Por lo tanto, el signo de la impedancia intrínseca sigue siendo positivo en un NIM. ^{[46] [47]}

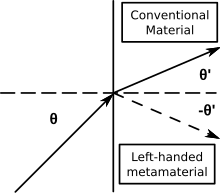
La luz que incide sobre un material levógiro, o NIM, se desviará hacia el mismo lado que el haz incidente y, para que se cumpla la ley de Snell, el ángulo de refracción debe ser negativo. En un medio metamaterial pasivo, esto determina una parte negativa real e imaginaria del índice de refracción. ^{[3] [46] [47]}

En 1968, el artículo de Victor Veselago mostró que las direcciones opuestas de las ondas planas EM y el flujo de energía se derivaban de las ecuaciones individuales del rizo de Maxwell . En los materiales ópticos ordinarios , la ecuación del rizo para el campo eléctrico muestra una "regla de la mano derecha" para las direcciones del campo eléctrico E , la inducción magnética B y la propagación de la onda, que va en la dirección del vector de onda k . Sin embargo, la dirección del flujo de energía formado por E × H es dextrógira solo cuando la permeabilidad es mayor que cero . Esto significa que cuando la permeabilidad es menor que cero, por ejemplo, negativa , la propagación de la onda se invierte (determinada por k) y es contraria a la dirección del flujo de energía. Además, las relaciones de los vectores E , H y k forman un sistema "zurdo" - y fue Veselago quien acuñó el término material "zurdo" (LH), que se usa ampliamente hoy en día (2011). Sostuvo que un material LH tiene un índice de refracción negativo y se basó en las soluciones de estado estable de las ecuaciones de Maxwell como centro de su argumento. ^[48]

Después de un vacío de 30 años, cuando finalmente se demostraron los materiales LH, se podría decir que la designación de índice de refracción negativo es exclusiva de los sistemas LH; incluso cuando se comparan con los cristales fotónicos . Los cristales fotónicos, como muchos otros sistemas conocidos, pueden exhibir un comportamiento de propagación inusual, como inversión de fase y velocidades de grupo. Pero la refracción negativa no ocurre en estos sistemas, y aún no de manera realista en los cristales fotónicos. ^{[48] [49] [50]}

El índice de refracción negativo en el rango óptico fue demostrado por primera vez en 2005 por Shalaev et al. (en la longitud de onda de telecomunicaciones λ = 1,5 μm) ^[17] y por Brueck et al. (en λ = 2 μm) casi al mismo tiempo. ^[51]

En 2006, un equipo de Caltech dirigido por Lezec, Dionne y Atwater logró una refracción negativa en el régimen espectral visible. ^{[52] [53] [54]}

Además de los valores invertidos para el índice de refracción , Veselago predijo la aparición de radiación Cherenkov invertida en un medio zurdo. Mientras que la radiación Cherenkov ordinaria se emite en un cono alrededor de la dirección en la que una partícula cargada viaja a través del medio, la radiación Cherenkov invertida se emite en un cono alrededor de la dirección opuesta. La radiación Cherenkov invertida se demostró experimentalmente por primera vez de forma indirecta en 2009, utilizando una matriz de dipolos electromagnéticos en fase para modelar una partícula cargada en movimiento. ^{[55] [56]} La radiación Cherenkov invertida emitida por partículas cargadas reales se observó por primera vez en 2017. ^[57]

El trabajo teórico, junto con las simulaciones numéricas , comenzó a principios de la década de 2000 sobre las capacidades de las placas DNG para el enfoque de sublongitud de onda . La investigación comenzó con la " Lente perfecta " propuesta por Pendry . Varias investigaciones posteriores a Pendry concluyeron que la "Lente perfecta" era posible en teoría pero poco práctica. Una dirección en el enfoque de sublongitud de onda procedió con el uso de metamateriales de índice negativo, pero basado en las mejoras para la formación de imágenes con plasmones de superficie. En otra dirección, los investigadores exploraron aproximaciones paraxiales de placas NIM. ^[3]

La existencia de materiales refractivos negativos puede dar lugar a un cambio en los cálculos electrodinámicos para el caso de permeabilidad μ = 1. Un cambio de un índice de refracción convencional a un valor negativo da resultados incorrectos para los cálculos convencionales, porque se han alterado algunas propiedades y efectos. Cuando la permeabilidad μ tiene valores distintos de 1 esto afecta a la ley de Snell , el efecto Doppler , la radiación de Cherenkov , las ecuaciones de Fresnel y el principio de Fermat . ^[10]

El índice de refracción es fundamental para la ciencia de la óptica. Cambiar el índice de refracción a un valor negativo puede ser motivo para revisar o reconsiderar la interpretación de algunas normas o leyes básicas . ^[23]

La primera patente estadounidense para un metamaterial fabricado, titulada "Medio compuesto para zurdos" de David R. Smith , Sheldon Schultz, Norman Kroll y Richard A. Shelby, se emitió en 2004. La invención logra permitividad y permeabilidad negativas simultáneas en una banda común de frecuencias. El material puede integrar medios que ya son compuestos o continuos, pero que producirán permitividad y permeabilidad negativas dentro del mismo espectro de frecuencias. Se pueden considerar apropiados diferentes tipos de continuos o compuestos cuando se combinan para el efecto deseado. Sin embargo, se prefiere la inclusión de una matriz periódica de elementos conductores. La matriz dispersa la radiación electromagnética en longitudes de onda más largas que el tamaño del elemento y el espaciado reticular. La matriz se considera entonces como un medio eficaz . ^[58]

Revistas académicas

• Metamateriales

Libros sobre metamateriales

• Manual de metamateriales
• Metamateriales: Exploraciones en Física e Ingeniería

 Este artículo incorpora material de dominio público de sitios web o documentos del Gobierno de los Estados Unidos . - NIST

• S. Anantha Ramakrishna; Tomasz M. Grzegorczyk (2008). Física y aplicaciones de materiales con índice de refracción negativo (PDF) . CRC Press. doi :10.1201/9781420068764.ch1 (inactivo 2024-11-12). ISBN 978-1-4200-6875-7. Archivado desde el original (PDF) el 3 de marzo de 2016.{{cite book}}: CS1 maint: DOI inactivo a partir de noviembre de 2024 ( enlace )
• Ramakrishna, S Anantha (2005). "Física de materiales con índice de refracción negativo". Informes sobre el progreso en física . 68 (2): 449. Bibcode :2005RPPh...68..449R. doi :10.1088/0034-4885/68/2/R06. S2CID  250829241.

• Pendry, J.; Holden, A.; Stewart, W.; Youngs, I. (1996). "Plasmones de frecuencia extremadamente baja en mesoestructuras metálicas" (PDF) . Physical Review Letters . 76 (25): 4773–4776. Bibcode :1996PhRvL..76.4773P. doi :10.1103/PhysRevLett.76.4773. PMID  10061377. Archivado desde el original (PDF) el 2011-07-17 . Consultado el 2011-08-18 .

• Pendry, JB; Holden, AJ; Robbins, DJ; Stewart, WJ (1998). "Plasmones de baja frecuencia en estructuras de alambre delgado" (PDF) . Journal of Physics: Condensed Matter . 10 (22): 4785–4809. Bibcode :1998JPCM...10.4785P. doi :10.1088/0953-8984/10/22/007. S2CID  250891354. Véase también la copia del autor de la preimpresión.
• Padilla, Willie J.; Basov, Dimitri N.; Smith, David R. (2006). "Metamateriales con índice de refracción negativo". Materials Today . 9 (7–8): 28. doi : 10.1016/S1369-7021(06)71573-5 .
• Bayindir, Mehmet; Aydin, K.; Ozbay, E.; Markoš, P.; Soukoulis, CM (1 de julio de 2002). "Propiedades de transmisión de metamateriales compuestos en el espacio libre" (PDF) . Applied Physics Letters . 81 (1): 120. Bibcode :2002ApPhL..81..120B. doi :10.1063/1.1492009. hdl : 11693/24684 .^{[ enlace muerto ]}

• Manipulación del campo cercano con metamateriales Presentación de diapositivas, con audio disponible, a cargo del Dr. John Pendry, Imperial College, Londres
• Laszlo Solymar; Ekaterina Shamonina (15 de marzo de 2009). Ondas en metamateriales. Oxford University Press, EE. UU., marzo de 2009. ISBN 978-0-19-921533-1.
• "Ilustrando la ley de refracción".
• Young, Andrew T. (1999–2009). "An Introduction to Mirages". SDSU San Diego, CA. Consultado el 12 de agosto de 2009 .
• Garrett, C.; et al. (25 de septiembre de 1969). "Pulso de luz y dispersión análoga" (PDF) . Phys. Rev. A . 1 (2): 305–313. Bibcode :1970PhRvA...1..305G. doi :10.1103/PhysRevA.1.305.^{[ enlace muerto permanente ]}
• Lista de artículos de noticias de sitios web científicos sobre materiales para zurdos
• Caloz, Christophe (marzo de 2009). "Perspectivas sobre metamateriales EM". Materials Today . 12 (3): 12–20. doi : 10.1016/S1369-7021(09)70071-9 .