Estacionalidad
Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes )
|
En los datos de series temporales , la estacionalidad se refiere a las tendencias que ocurren en intervalos regulares específicos menores a un año, como semanalmente, mensualmente o trimestralmente. La estacionalidad puede ser causada por varios factores, como el clima, las vacaciones y los días festivos [1] y consiste en patrones periódicos, repetitivos y generalmente regulares y predecibles en los niveles [2] de una serie temporal.
Las fluctuaciones estacionales en una serie temporal pueden contrastarse con los patrones cíclicos. Estos últimos ocurren cuando los datos presentan altibajos que no corresponden a un período fijo. Estas fluctuaciones no estacionales suelen deberse a las condiciones económicas y suelen estar relacionadas con el "ciclo económico"; su período suele extenderse más allá de un solo año y las fluctuaciones suelen durar al menos dos años. [3]
Las organizaciones que se enfrentan a variaciones estacionales, como las vendedoras de helados, suelen estar interesadas en conocer su desempeño en relación con la variación estacional normal. Las variaciones estacionales en el mercado laboral pueden atribuirse a la entrada de los jóvenes que abandonan la escuela en el mercado laboral, ya que su objetivo es contribuir a la fuerza laboral una vez que terminan sus estudios. Estos cambios regulares son de menor interés para quienes estudian los datos de empleo que las variaciones que se producen debido al estado subyacente de la economía; su atención se centra en cómo ha cambiado el desempleo en la fuerza laboral, a pesar del impacto de las variaciones estacionales regulares. [3]
Las organizaciones necesitan identificar y medir las variaciones estacionales dentro de su mercado para ayudarlas a planificar el futuro. Esto puede prepararlas para los aumentos o disminuciones temporales en los requisitos de mano de obra y el inventario a medida que la demanda de su producto o servicio fluctúa durante ciertos períodos. Esto puede requerir capacitación, mantenimiento periódico, etc., que se pueden organizar con anticipación. Además de estas consideraciones, las organizaciones necesitan saber si la variación que han experimentado ha sido mayor o menor que la cantidad esperada, más allá de lo que representan las variaciones estacionales habituales. [4]
Motivación
Hay varias razones principales para estudiar la variación estacional:
- La descripción del efecto estacional proporciona una mejor comprensión del impacto que este componente tiene sobre una serie particular.
- Una vez establecido el patrón estacional, se pueden implementar métodos para eliminarlo de la serie temporal y estudiar el efecto de otros componentes, como las variaciones cíclicas e irregulares. Esta eliminación del efecto estacional se denomina desestacionalización o ajuste estacional de los datos.
- Utilizar los patrones pasados de las variaciones estacionales para contribuir a la previsión y predicción de las tendencias futuras, como en las normales climáticas .
Detección
Se pueden utilizar las siguientes técnicas gráficas para detectar la estacionalidad:
- Un gráfico de secuencia de ejecución a menudo mostrará estacionalidad.

Gráfico de estacionalidad del consumo de electricidad en EE. UU. - Un gráfico estacional mostrará los datos de cada estación superpuestos [5]
- Un gráfico de subserie estacional es una técnica especializada para mostrar la estacionalidad.
- Se pueden utilizar diagramas de cajas múltiples como alternativa al gráfico de subseries estacionales para detectar la estacionalidad.
- Un gráfico de autocorrelación (ACF) y un gráfico espectral pueden ayudar a identificar la estacionalidad.
Una muy buena manera de encontrar periodicidad, incluida la estacionalidad, en cualquier serie regular de datos es eliminar primero cualquier tendencia general y luego inspeccionar la periodicidad temporal. [6]
El gráfico de secuencia de series es un primer paso recomendado para analizar cualquier serie temporal. Aunque a veces la estacionalidad se puede indicar mediante este gráfico, la estacionalidad se muestra más claramente mediante el gráfico de subseries estacionales o el gráfico de cajas. El gráfico de subseries estacionales hace un excelente trabajo al mostrar tanto las diferencias estacionales (entre patrones de grupo) como también los patrones dentro del grupo. El gráfico de cajas muestra la diferencia estacional (entre patrones de grupo) bastante bien, pero no muestra los patrones dentro del grupo. Sin embargo, para conjuntos de datos grandes, el gráfico de cajas suele ser más fácil de leer que el gráfico de subseries estacionales.
El gráfico estacional, el gráfico de subseries estacionales y el gráfico de cajas suponen que se conocen los períodos estacionales. En la mayoría de los casos, el analista lo sabrá. Por ejemplo, para los datos mensuales, el período es 12, ya que hay 12 meses en un año. Sin embargo, si no se conoce el período, el gráfico de autocorrelación puede ayudar. Si hay una estacionalidad significativa, el gráfico de autocorrelación debería mostrar picos en los rezagos iguales al período. Por ejemplo, para los datos mensuales, si hay un efecto de estacionalidad, esperaríamos ver picos significativos en los rezagos 12, 24, 36, etc. (aunque la intensidad puede disminuir a medida que avanzamos).
Se puede utilizar un gráfico de autocorrelación (ACF) para identificar la estacionalidad, ya que calcula la diferencia (cantidad residual) entre un valor de Y y un valor rezagado de Y. El resultado arroja algunos puntos en los que los dos valores están muy próximos entre sí (sin estacionalidad), pero otros puntos en los que hay una gran discrepancia. Estos puntos indican un nivel de estacionalidad en los datos.
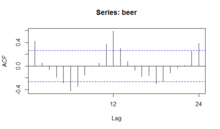
Las variaciones cíclicas semirregulares podrían abordarse mediante la estimación de la densidad espectral .
Cálculo
La variación estacional se mide en términos de un índice, llamado índice estacional. Es un promedio que se puede utilizar para comparar una observación real con lo que sería si no hubiera variación estacional. Se asigna un valor de índice a cada período de la serie temporal dentro de un año. Esto implica que si se consideran los datos mensuales, hay 12 índices estacionales separados, uno para cada mes. Los siguientes métodos utilizan índices estacionales para medir las variaciones estacionales de los datos de una serie temporal.
- Método de promedios simples
- Método de relación con la tendencia
- Método de relación con el promedio móvil
- Método de vinculación de parientes
Método de promedios simples
La medición de la variación estacional mediante el método de la relación con el promedio móvil proporciona un índice para medir el grado de variación estacional en una serie temporal. El índice se basa en una media de 100, y el grado de estacionalidad se mide por las variaciones que se alejan de la base. Por ejemplo, si observamos los alquileres de un hotel en un complejo invernal, encontramos que el índice del trimestre de invierno es 124. El valor 124 indica que el 124 por ciento del alquiler trimestral promedio se produce en invierno. Si la administración del hotel registra 1436 alquileres durante todo el año pasado, entonces el alquiler trimestral promedio sería 359 = (1436/4). Como el índice del trimestre de invierno es 124, estimamos el número de alquileres de invierno de la siguiente manera:
359*(124/100)=445;
Aquí, 359 es el alquiler trimestral promedio. 124 es el índice del trimestre de invierno. 445 es el alquiler estacionalizado del trimestre de invierno.
Este método también se denomina método de promedio móvil porcentual . En este método, los valores de los datos originales de la serie temporal se expresan como porcentajes de promedios móviles. Los pasos y las tabulaciones se indican a continuación.
Método de relación con la tendencia
- Encuentre los promedios móviles centrados de 12 meses (o 4 trimestrales) de los valores de datos originales en la serie de tiempo .
- Expresar cada valor de datos originales de la serie temporal como un porcentaje de los valores de promedio móvil centrados correspondientes obtenidos en el paso (1). En otras palabras, en un modelo de serie temporal multiplicativo, obtenemos (valores de datos originales) / (valores de tendencia) × 100 = ( T × C × S × I ) / ( T × C ) × 100 = ( S × I ) × 100.
Esto implica que la relación con el promedio móvil representa los componentes estacional e irregular. - Ordena estos porcentajes por meses o trimestres de los años indicados. Encuentra los promedios de todos los meses o trimestres de los años indicados.
- Si la suma de estos índices no es 1200 (o 400 para cifras trimestrales), se multiplica por un factor de corrección = 1200 / (suma de los índices mensuales). En caso contrario, los 12 promedios mensuales se considerarán índices estacionales.
Método de relación con el promedio móvil
Calculemos el índice estacional mediante el método de razón-promedio móvil a partir de los siguientes datos:
| Año/Trimestres | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1996 | 75 | 60 | 54 | 59 |
| 1997 | 86 | 65 | 63 | 80 |
| 1998 | 90 | 72 | 66 | 85 |
| 1999 | 100 | 78 | 72 | 93 |
Ahora los cálculos para 4 promedios móviles trimestrales y la relación con los promedios móviles se muestran en la siguiente tabla.
| Año | Cuarto | Valores originales (Y) | 4 cifras totales móviles | Promedio móvil de 4 cifras | 2 cifras totales móviles | Promedio móvil de 2 cifras (T) | Relación con la media móvil (%)(Y)/ (T)*100 |
|---|---|---|---|---|---|---|---|
| 1996 | 1 | 75 | — | — | — | ||
| — | — | ||||||
| 2 | 60 | — | — | — | |||
| 248 | 62,00 | ||||||
| 3 | 54 | 126,75 | 63.375 | 85.21 | |||
| 259 | 64,75 | ||||||
| 4 | 59 | 130,75 | 65.375 | 90,25 | |||
| 264 | 66,00 | ||||||
| 1997 | 1 | 86 | 134,25 | 67.125 | 128.12 | ||
| 273 | 68,25 | ||||||
| 2 | 65 | 141,75 | 70.875 | 91,71 | |||
| 294 | 73,50 | ||||||
| 3 | 63 | 148,00 | 74,00 | 85.13 | |||
| 298 | 74,50 | ||||||
| 4 | 80 | 150,75 | 75.375 | 106.14 | |||
| 305 | 76,25 | ||||||
| 1998 | 1 | 90 | 153,25 | 76.625 | 117,45 | ||
| 308 | 77,00 | ||||||
| 2 | 72 | 155,25 | 77.625 | 92,75 | |||
| 313 | 78,25 | ||||||
| 3 | 66 | 159,00 | 79,50 | 83.02 | |||
| 323 | 80,75 | ||||||
| 4 | 85 | 163,00 | 81,50 | 104.29 | |||
| 329 | 82,25 | ||||||
| 1999 | 1 | 100 | 166,00 | 83.00 | 120,48 | ||
| 335 | 83,75 | ||||||
| 2 | 78 | 169,50 | 84,75 | 92.03 | |||
| 343 | 85,75 | ||||||
| 3 | 72 | — | — | — | |||
| — | — | ||||||
| 4 | 93 | — | — | — | |||
| Años/Trimestres | 1 | 2 | 3 | 4 | Total |
|---|---|---|---|---|---|
| 1996 | — | — | 85.21 | 90,25 | |
| 1997 | 128.12 | 91,71 | 85.13 | 106.14 | |
| 1998 | 117,45 | 92,75 | 83.02 | 104.29 | |
| 1999 | 120,48 | 92.04 | — | — | |
| Total | 366.05 | 276,49 | 253.36 | 300,68 | |
| Promedio estacional | 122.01 | 92,16 | 84,45 | 100.23 | 398,85 |
| Promedio estacional ajustado | 122.36 | 92,43 | 84,69 | 100,52 | 400 |
Ahora, el total de promedios estacionales es 398,85. Por lo tanto, el factor de corrección correspondiente sería 400/398,85 = 1,00288. Cada promedio estacional se multiplica por el factor de corrección 1,00288 para obtener los índices estacionales ajustados, como se muestra en la tabla anterior.
Método de vinculación de parientes
1. En un modelo aditivo de series temporales, el componente estacional se estima como:
- S = Y – ( T + C + I )
dónde
- S : Valores estacionales
- Y : Valores de datos reales de la serie temporal
- T : Valores de tendencia
- C : Valores cíclicos
- I : Valores irregulares.
2. En un modelo de series de tiempo multiplicativo, el componente estacional se expresa en términos de razón y porcentaje como
- Efecto estacional ;
Sin embargo, en la práctica la eliminación de la tendencia de las series temporales se realiza para llegar a .
Esto se hace dividiendo ambos lados de por los valores de tendencia T de modo que .
3. Los datos de series temporales desestacionalizadas tendrán únicamente componentes de tendencia ( T ), cíclicos ( C ) e irregulares ( I ) y se expresan como:
- Modelo multiplicativo:
- Modelo aditivo : Y – S = ( T + S + C + I ) – S = T + C + I
Modelado
Una variación cíclica completamente regular en una serie temporal podría abordarse en el análisis de series temporales utilizando un modelo sinusoidal con una o más sinusoides cuyas longitudes de período pueden ser conocidas o desconocidas según el contexto. Una variación cíclica menos completamente regular podría abordarse utilizando una forma especial de un modelo ARIMA que puede estructurarse de modo de tratar las variaciones cíclicas de manera semiexplícita. Dichos modelos representan procesos cicloestacionarios .
Otro método para modelar la estacionalidad periódica es el uso de pares de términos de Fourier. De manera similar al uso del modelo sinusoidal, los términos de Fourier agregados a los modelos de regresión utilizan términos seno y coseno para simular la estacionalidad. Sin embargo, la estacionalidad de dicha regresión se representaría como la suma de los términos seno o coseno, en lugar de un solo término seno o coseno en un modelo sinusoidal. Cada función periódica se puede aproximar con la inclusión de términos de Fourier.
La diferencia entre un modelo sinusoidal y una regresión con términos de Fourier se puede simplificar de la siguiente manera:
Modelo sinusoidal:
Regresión con términos de Fourier:
Ajuste estacional
El ajuste estacional o desestacionalización es cualquier método para eliminar el componente estacional de una serie temporal . Los datos resultantes ajustados estacionalmente se utilizan, por ejemplo, al analizar o informar sobre tendencias no estacionales durante períodos más largos que el estacional. Se elige un método adecuado para el ajuste estacional sobre la base de una visión particular adoptada de la descomposición de la serie temporal en componentes designados con nombres como "tendencia", "cíclico", "estacional" e "irregular", incluida la forma en que interactúan entre sí. Por ejemplo, dichos componentes pueden actuar de forma aditiva o multiplicativa. Por lo tanto, si un componente estacional actúa de forma aditiva, el método de ajuste tiene dos etapas:
- estimar el componente estacional de la variación en la serie temporal, generalmente en una forma que tiene una media cero en todas las series;
- restar el componente estacional estimado de la serie temporal original, dejando la serie ajustada estacionalmente: . [3]
Si se trata de un modelo multiplicativo, la magnitud de las fluctuaciones estacionales variará con el nivel, lo que es más probable que ocurra con las series económicas. [3] Al tener en cuenta la estacionalidad, la descomposición multiplicativa ajustada estacionalmente se puede escribir como ; donde la serie temporal original se divide por el componente estacional estimado.
El modelo multiplicativo se puede transformar en un modelo aditivo tomando el logaritmo de la serie temporal;
Descomposición multiplicativa SA:
Tomando el logaritmo de la serie temporal del modelo multiplicativo: [3]
Una implementación particular del ajuste estacional la proporciona X-12-ARIMA .
En el análisis de regresión
En el análisis de regresión , como los mínimos cuadrados ordinarios , en el que una variable dependiente que varía estacionalmente está influida por una o más variables independientes , la estacionalidad se puede tener en cuenta y medir incluyendo n -1 variables ficticias , una para cada una de las estaciones, excepto para una estación de referencia elegida arbitrariamente, donde n es el número de estaciones (por ejemplo, 4 en el caso de estaciones meteorológicas, 12 en el caso de meses, etc.). Cada variable ficticia se establece en 1 si el punto de datos se extrae de la estación especificada de la variable ficticia y 0 en caso contrario. Luego, el valor predicho de la variable dependiente para la estación de referencia se calcula a partir del resto de la regresión, mientras que para cualquier otra estación se calcula utilizando el resto de la regresión e insertando el valor 1 para la variable ficticia para esa estación.
Patrones relacionados
Es importante distinguir los patrones estacionales de los patrones relacionados. Mientras que un patrón estacional ocurre cuando una serie temporal se ve afectada por la estación o la época del año, como anual, semestral, trimestral, etc. Un patrón cíclico , o simplemente un ciclo , ocurre cuando los datos presentan subidas y bajadas en otros períodos, es decir, mucho más largos (p. ej., decenal ) o mucho más cortos (p. ej., semanal ) que el estacional. Una cuasiperiodicidad es una periodicidad irregular más general.
Véase también
Referencias
- ^ "Estacionalidad".|title=Factores influyentes|
- ^ "Copia archivada". Archivado desde el original el 18 de mayo de 2015. Consultado el 13 de mayo de 2015 .
{{cite web}}: CS1 maint: copia archivada como título ( enlace ) - ^ abcde 6.1 Componentes de series de tiempo - OTexts.
- ^ "2 consejos para maximizar las ganancias en los negocios". netsuite .
- ^ 2.1 Gráficos - OTextos.
- ^ "Series temporales: ¿qué método se puede utilizar para detectar la estacionalidad de los datos?". Validación cruzada .
Lectura adicional
- Franses, Philip Hans (1996). Periodicidad y tendencias estocásticas en series temporales económicas . Nueva York: Oxford University Press. ISBN 0-19-877454-0.
- Ghysels, Eric; Osborn, Denise R. (2001). El análisis econométrico de series temporales estacionales . Cambridge: Cambridge University Press. ISBN 0-521-56588-X.
- Hylleberg, Svend (1986). Estacionalidad en la regresión . Orlando: Academic Press. ISBN 0-12-363455-5.
- Hyndman, Rob J.; Athansopoulos, George (2021). Pronóstico: práctica y principios (3.ª ed.). ISBN 978-0-9875071-3-6.
Enlaces externos
 Medios relacionados con la estacionalidad en Wikimedia Commons
Medios relacionados con la estacionalidad en Wikimedia Commons- Estacionalidad en el manual electrónico de métodos estadísticos del NIST/SEMATECH
![]() Este artículo incorpora material de dominio público del Manual electrónico de métodos estadísticos del NIST/SEMATECH. Instituto Nacional de Estándares y Tecnología .
Este artículo incorpora material de dominio público del Manual electrónico de métodos estadísticos del NIST/SEMATECH. Instituto Nacional de Estándares y Tecnología .















