Mapa lineal

Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . Ayúdenos a mejorar este artículo introduciendo citas más precisas. ( Diciembre de 2021 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En matemáticas , y más específicamente en álgebra lineal , una función lineal (también llamada aplicación lineal , transformación lineal , homomorfismo de espacio vectorial o, en algunos contextos, función lineal ) es una aplicación entre dos espacios vectoriales que conserva las operaciones de adición de vectores y multiplicación escalar . Los mismos nombres y la misma definición también se utilizan para el caso más general de módulos sobre un anillo ; véase Homomorfismo de módulos .${\displaystyle V\to W}$

Si un mapa lineal es una biyección entonces se llamaisomorfismo lineal . En el caso en que, una función lineal se denominaendomorfismo lineal. A veces el término${\estilo de visualización V=W}$El operador lineal se refiere a este caso,^[1]pero el término "operador lineal" puede tener diferentes significados para diferentes convenciones: por ejemplo, se puede usar para enfatizar queysonespacios vectorialesreales),^{[ cita requerida ]}o se puede usar para enfatizar quees unespacio de funciones, que es una convención común enel análisis funcional.^[2]A veces, el término función lineal tiene el mismo significado quemapa lineal, mientras que enel análisisno.${\estilo de visualización V}$${\estilo de visualización W}$${\estilo de visualización V=W}$${\estilo de visualización V}$

Una función lineal de a siempre asigna el origen de al origen de . Además, asigna subespacios lineales en a subespacios lineales en (posiblemente de una dimensión menor ); ^[3] por ejemplo, asigna un plano que pasa por el origen en a un plano que pasa por el origen en , una línea que pasa por el origen en o simplemente el origen en . Las funciones lineales a menudo se pueden representar como matrices , y ejemplos simples incluyen transformaciones lineales de rotación y reflexión .${\estilo de visualización V}$${\estilo de visualización W}$${\estilo de visualización V}$${\estilo de visualización W}$${\estilo de visualización V}$${\estilo de visualización W}$${\estilo de visualización V}$${\estilo de visualización W}$${\estilo de visualización W}$${\estilo de visualización W}$

En el lenguaje de la teoría de categorías , los mapas lineales son los morfismos de los espacios vectoriales y forman una categoría equivalente a la de las matrices .

Sean y espacios vectoriales sobre el mismo cuerpo . Se dice que una función es una función lineal si para dos vectores cualesquiera y cualquier escalar se cumplen las dos condiciones siguientes:${\estilo de visualización V}$${\estilo de visualización W}$ ${\estilo de visualización K}$${\displaystyle f:V\to W}$${\textstyle \mathbf {u} ,\mathbf {v} \en V}$${\displaystyle c\en K}$

• Aditividad / operación de adición$${\displaystyle f(\mathbf {u} +\mathbf {v} )=f(\mathbf {u} )+f(\mathbf {v} )}$$
• Homogeneidad de grado 1 / operación de multiplicación escalar$${\displaystyle f(c\mathbf {u} )=cf(\mathbf {u} )}$$

Por lo tanto, se dice que una función lineal preserva las operaciones . En otras palabras, no importa si la función lineal se aplica antes (los lados derechos de los ejemplos anteriores) o después (los lados izquierdos de los ejemplos) de las operaciones de adición y multiplicación escalar.

Por la asociatividad de la operación de adición denotada como +, para cualesquiera vectores y escalares se cumple la siguiente igualdad: ^{[4] [5]} Por lo tanto, una función lineal es una que preserva las combinaciones lineales .${\textstyle \mathbf {u} _{1},\ldots ,\mathbf {u} _{n}\in V}$${\textstyle c_{1},\ldots ,c_{n}\en K,}$$${\displaystyle f(c_{1}u_{1}+\cdots +c_{n}u_{n})=c_{1}f(u_{1})+\cdots +c_{n}f(u_{n}).}$$

Denotando los elementos cero de los espacios vectoriales y por y respectivamente, se sigue que Sea y en la ecuación de homogeneidad de grado 1:${\estilo de visualización V}$${\estilo de visualización W}$${\textstyle \mathbf {0} _{V}}$${\textstyle \mathbf {0} _{W}}$${\textstyle f(\mathbf {0} _{V})=\mathbf {0} _{W}.}$${\estilo de visualización c=0}$${\textstyle \mathbf {v} \en V}$$${\displaystyle f(\mathbf {0} _{V})=f(0\mathbf {v} )=0f(\mathbf {v} )=\mathbf {0} _{W}.}$$

Un mapa lineal considerado como un espacio vectorial unidimensional sobre sí mismo se denomina funcional lineal . ^[6]${\displaystyle V\to K}$${\estilo de visualización K}$

Estas afirmaciones se generalizan a cualquier módulo izquierdo sobre un anillo sin modificación, y a cualquier módulo derecho al invertir la multiplicación escalar.${\textstyle {}_{R}M}$${\estilo de visualización R}$

• Un ejemplo prototípico que da a los mapas lineales su nombre es una función , cuyo gráfico es una línea que pasa por el origen. ^[7]${\displaystyle f:\mathbb {R} \to \mathbb {R} :x\mapsto cx}$
• De manera más general, cualquier homotecia centrada en el origen de un espacio vectorial es una función lineal (aquí c es un escalar).${\textstyle \mathbf {v} \mapsto c\mathbf {v} }$
• El mapa cero entre dos espacios vectoriales (sobre el mismo campo ) es lineal.${\textstyle \mathbf {x} \mapsto \mathbf {0} }$
• El mapa de identidad de cualquier módulo es un operador lineal.
• Para números reales, el mapa no es lineal.${\textstyle x\mapsto x^{2}}$
• Para los números reales, la función no es lineal (sino que es una transformación afín ).${\textstyle x\mapsto x+1}$
• Si es una matriz real , entonces define una función lineal de a enviando un vector columna al vector columna . A la inversa, cualquier función lineal entre espacios vectoriales de dimensión finita se puede representar de esta manera; consulte el § Matrices, a continuación.${\estilo de visualización A}$${\displaystyle m\veces n}$ ${\estilo de visualización A}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$${\displaystyle A\mathbf {x} \en \mathbb {R} ^{m}}$
• Si es una isometría entre espacios normados reales tal que entonces es una función lineal. Este resultado no es necesariamente cierto para espacios normados complejos. ^[8]${\textstyle f:V\to W}$${\textstyle f(0)=0}$${\estilo de visualización f}$
• La diferenciación define una función lineal desde el espacio de todas las funciones diferenciables al espacio de todas las funciones. También define un operador lineal en el espacio de todas las funciones suaves (un operador lineal es un endomorfismo lineal , es decir, una función lineal con el mismo dominio y codominio ). De hecho,$${\displaystyle {\frac {d}{dx}}(af(x)+bg(x)\right)=a{\frac {df(x)}{dx}}+b{\frac {dg(x)}{dx}}.}$$
• Una integral definida sobre un intervalo I es una función lineal del espacio de todas las funciones integrables de valor real en I a . De hecho,${\displaystyle \mathbb {R}}$$${\displaystyle \int _{u}^{v}\left(af(x)+bg(x)\right)dx=a\int _{u}^{v}f(x)dx+b\int _{u}^{v}g(x)dx.}$$
• Una integral indefinida (o antiderivada ) con un punto de inicio de integración fijo define una función lineal desde el espacio de todas las funciones integrables de valor real hasta el espacio de todas las funciones diferenciables de valor real en . Sin un punto de inicio fijo, la antiderivada se aplica al espacio cociente de las funciones diferenciables por el espacio lineal de funciones constantes.${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {R}}$
• Si y son espacios vectoriales de dimensión finita sobre un cuerpo F , de dimensiones respectivas m y n , entonces la función que asigna aplicaciones lineales a matrices n × m de la manera descrita en § Matrices (abajo) es una aplicación lineal, e incluso un isomorfismo lineal .${\estilo de visualización V}$${\estilo de visualización W}$${\textstyle f:V\to W}$
• El valor esperado de una variable aleatoria (que de hecho es una función y, como tal, un elemento de un espacio vectorial) es lineal, como para las variables aleatorias y tenemos y , pero la varianza de una variable aleatoria no es lineal.${\estilo de visualización X}$${\estilo de visualización Y}$${\displaystyle E[X+Y]=E[X]+E[Y]}$${\displaystyle E[aX]=aE[X]}$

• 
  La función con es una función lineal. Esta función escala el componente de un vector por el factor .${\textstyle f:\mathbb {R} ^{2}\to \mathbb {R} ^{2}}$${\textstyle f(x,y)=(2x,y)}$${\textstyle x}$${\estilo de texto 2}$
• 
  La función es aditiva: no importa si los vectores primero se suman y luego se asignan o si se asignan y finalmente se suman:${\textstyle f(x,y)=(2x,y)}$${\textstyle f(\mathbf {a} +\mathbf {b} )=f(\mathbf {a} )+f(\mathbf {b} )}$
• 
  La función es homogénea: no importa si un vector primero se escala y luego se mapea o primero se mapea y luego se escala:${\textstyle f(x,y)=(2x,y)}$${\textstyle f(\lambda \mathbf {a} )=\lambda f(\mathbf {a} )}$

A menudo, un mapa lineal se construye definiéndolo en un subconjunto de un espacio vectorial y luegoextendiéndose por linealidad hasta elespacio linealdel dominio. Supóngaseque yson espacios vectoriales yes unafuncióndefinida en algún subconjunto. Entonces, una${\estilo de visualización X}$${\estilo de visualización Y}$${\displaystyle f:S\to Y}$${\displaystyle S\subseteq X.}$extensión lineal dea${\estilo de visualización f}$${\estilo de visualización X,}$si existe, es una función linealdefinida enqueextiende^{[nota 1]}(lo que significa quepara todos) y toma sus valores del codominio de^[9] Cuando el subconjuntoes un subespacio vectorial deentonces se garantiza que existe unaextensión lineal (-valuada) dea todos desi (y solo si)es una función lineal.^[9]En particular, sitiene una extensión lineal aentonces tiene una extensión lineal a todos de${\displaystyle F:X\a Y}$${\estilo de visualización X}$ ${\estilo de visualización f}$${\displaystyle F(s)=f(s)}$${\displaystyle s\en S}$${\estilo de visualización f.}$${\estilo de visualización S}$${\estilo de visualización X}$${\estilo de visualización Y}$${\estilo de visualización f}$${\estilo de visualización X}$${\displaystyle f:S\to Y}$${\estilo de visualización f}$${\displaystyle \operatorname {span} S,}$${\estilo de visualización X.}$

El mapa se puede extender a un mapa lineal si y solo si siempre que es un entero, son escalares y son vectores tales que entonces necesariamente ^[10] Si existe una extensión lineal de entonces la extensión lineal es única y se cumple para todos y como se indicó anteriormente. ^[10] Si es linealmente independiente, entonces cada función en cualquier espacio vectorial tiene una extensión lineal a un mapa (lineal) (lo inverso también es cierto).${\displaystyle f:S\to Y}$${\displaystyle F:\nombreoperador {span} S\to Y}$${\estilo de visualización n>0}$${\displaystyle c_{1},\ldots ,c_{n}}$${\displaystyle s_{1},\ldots ,s_{n}\en S}$${\displaystyle 0=c_{1}s_{1}+\cdots +c_{n}s_{n},}$${\displaystyle 0=c_{1}f\left(s_{1}\right)+\cdots +c_{n}f\left(s_{n}\right).}$${\displaystyle f:S\to Y}$${\displaystyle F:\operatorname {span} S\to Y}$$${\displaystyle F\left(c_{1}s_{1}+\cdots c_{n}s_{n}\right)=c_{1}f\left(s_{1}\right)+\cdots +c_{n}f\left(s_{n}\right)}$$${\displaystyle n,c_{1},\ldots ,c_{n},}$${\displaystyle s_{1},\ldots ,s_{n}}$${\displaystyle S}$${\displaystyle f:S\to Y}$${\displaystyle \;\operatorname {span} S\to Y}$

Por ejemplo, si y entonces la asignación y se puede extender linealmente desde el conjunto linealmente independiente de vectores a un mapa lineal en La única extensión lineal es el mapa que envía a${\displaystyle X=\mathbb {R} ^{2}}$${\displaystyle Y=\mathbb {R} }$${\displaystyle (1,0)\to -1}$${\displaystyle (0,1)\to 2}$${\displaystyle S:=\{(1,0),(0,1)\}}$${\displaystyle \operatorname {span} \{(1,0),(0,1)\}=\mathbb {R} ^{2}.}$${\displaystyle F:\mathbb {R} ^{2}\to \mathbb {R} }$${\displaystyle (x,y)=x(1,0)+y(0,1)\in \mathbb {R} ^{2}}$$${\displaystyle F(x,y)=x(-1)+y(2)=-x+2y.}$$

Cada funcional lineal (de valor escalar) definido en un subespacio vectorial de un espacio vectorial real o complejo tiene una extensión lineal para todos los de De hecho, el teorema de extensión dominada de Hahn-Banach incluso garantiza que cuando este funcional lineal está dominado por alguna seminorma dada (lo que significa que se cumple para todos en el dominio de ), entonces existe una extensión lineal para que también está dominada por${\displaystyle f}$${\displaystyle X}$${\displaystyle X.}$${\displaystyle f}$ ${\displaystyle p:X\to \mathbb {R} }$${\displaystyle |f(m)|\leq p(m)}$${\displaystyle m}$${\displaystyle f}$${\displaystyle X}$${\displaystyle p.}$

Si y son espacios vectoriales de dimensión finita y se define una base para cada espacio vectorial, entonces cada función lineal de a puede representarse mediante una matriz . ^[11] Esto es útil porque permite cálculos concretos. Las matrices proporcionan ejemplos de funciones lineales: si es una matriz real , entonces describe una función lineal (véase espacio euclidiano ).${\displaystyle V}$${\displaystyle W}$${\displaystyle V}$${\displaystyle W}$${\displaystyle A}$${\displaystyle m\times n}$${\displaystyle f(\mathbf {x} )=A\mathbf {x} }$${\displaystyle \mathbb {R} ^{n}\to \mathbb {R} ^{m}}$

Sea una base para . Entonces cada vector está determinado de forma única por los coeficientes del campo :${\displaystyle \{\mathbf {v} _{1},\ldots ,\mathbf {v} _{n}\}}$${\displaystyle V}$${\displaystyle \mathbf {v} \in V}$${\displaystyle c_{1},\ldots ,c_{n}}$${\displaystyle \mathbb {R} }$$${\displaystyle \mathbf {v} =c_{1}\mathbf {v} _{1}+\cdots +c_{n}\mathbf {v} _{n}.}$$

Si es un mapa lineal,${\textstyle f:V\to W}$$${\displaystyle f(\mathbf {v} )=f(c_{1}\mathbf {v} _{1}+\cdots +c_{n}\mathbf {v} _{n})=c_{1}f(\mathbf {v} _{1})+\cdots +c_{n}f\left(\mathbf {v} _{n}\right),}$$

lo que implica que la función f está completamente determinada por los vectores . Ahora sea una base para . Entonces podemos representar cada vector como${\displaystyle f(\mathbf {v} _{1}),\ldots ,f(\mathbf {v} _{n})}$${\displaystyle \{\mathbf {w} _{1},\ldots ,\mathbf {w} _{m}\}}$${\displaystyle W}$${\displaystyle f(\mathbf {v} _{j})}$$${\displaystyle f\left(\mathbf {v} _{j}\right)=a_{1j}\mathbf {w} _{1}+\cdots +a_{mj}\mathbf {w} _{m}.}$$

Por lo tanto, la función está completamente determinada por los valores de . Si ponemos estos valores en una matriz , entonces podemos usarla convenientemente para calcular la salida vectorial de para cualquier vector en . Para obtener , cada columna de es un vector correspondiente a como se definió anteriormente. Para definirlo más claramente, para alguna columna que corresponde a la aplicación , donde es la matriz de . En otras palabras, cada columna tiene un vector correspondiente cuyas coordenadas son los elementos de la columna . Una única aplicación lineal puede estar representada por muchas matrices. Esto se debe a que los valores de los elementos de una matriz dependen de las bases elegidas.${\displaystyle f}$${\displaystyle a_{ij}}$${\displaystyle m\times n}$${\displaystyle M}$${\displaystyle f}$${\displaystyle V}$${\displaystyle M}$${\displaystyle j}$${\displaystyle M}$$${\displaystyle {\begin{pmatrix}a_{1j}\\\vdots \\a_{mj}\end{pmatrix}}}$$${\displaystyle f(\mathbf {v} _{j})}$${\displaystyle j}$${\displaystyle f(\mathbf {v} _{j})}$$${\displaystyle \mathbf {M} ={\begin{pmatrix}\ \cdots &a_{1j}&\cdots \ \\&\vdots &\\&a_{mj}&\end{pmatrix}}}$$${\displaystyle M}$${\displaystyle f}$${\displaystyle j=1,\ldots ,n}$${\displaystyle f(\mathbf {v} _{j})}$${\displaystyle a_{1j},\cdots ,a_{mj}}$${\displaystyle j}$

Las matrices de una transformación lineal se pueden representar visualmente:

1. Matriz para relativo a :${\textstyle T}$${\textstyle B}$${\textstyle A}$
2. Matriz para relativo a :${\textstyle T}$${\textstyle B'}$${\textstyle A'}$
3. Matriz de transición de a :${\textstyle B'}$${\textstyle B}$${\textstyle P}$
4. Matriz de transición de a :${\textstyle B}$${\textstyle B'}$${\textstyle P^{-1}}$

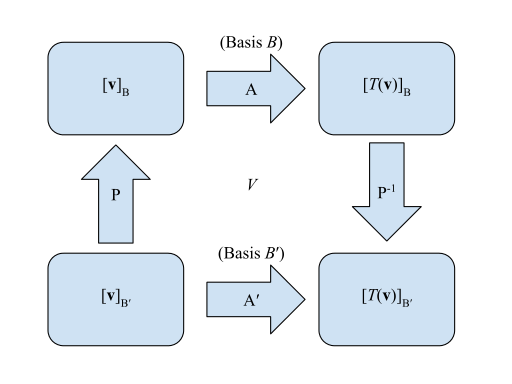
De modo que, comenzando en la esquina inferior izquierda y buscando la esquina inferior derecha , se multiplicaría por la izquierda, es decir, . El método equivalente sería el método "más largo" que se ejecuta en el sentido de las agujas del reloj desde el mismo punto, de modo que se multiplica por la izquierda con , o .${\textstyle \left[\mathbf {v} \right]_{B'}}$${\textstyle \left[T\left(\mathbf {v} \right)\right]_{B'}}$${\textstyle A'\left[\mathbf {v} \right]_{B'}=\left[T\left(\mathbf {v} \right)\right]_{B'}}$${\textstyle \left[\mathbf {v} \right]_{B'}}$${\textstyle P^{-1}AP}$${\textstyle P^{-1}AP\left[\mathbf {v} \right]_{B'}=\left[T\left(\mathbf {v} \right)\right]_{B'}}$

En el espacio bidimensional R ² se describen aplicaciones lineales mediante matrices de 2 × 2. Estos son algunos ejemplos:

• rotación
  • 90 grados en sentido antihorario:$${\displaystyle \mathbf {A} ={\begin{pmatrix}0&-1\\1&0\end{pmatrix}}}$$
  • por un ángulo θ en sentido antihorario:$${\displaystyle \mathbf {A} ={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}}}$$
• reflexión
  • a través del eje x :$${\displaystyle \mathbf {A} ={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}}$$
  • a través del eje y :$${\displaystyle \mathbf {A} ={\begin{pmatrix}-1&0\\0&1\end{pmatrix}}}$$
  • a través de una línea que forma un ángulo θ con el origen:$${\displaystyle \mathbf {A} ={\begin{pmatrix}\cos 2\theta &\sin 2\theta \\\sin 2\theta &-\cos 2\theta \end{pmatrix}}}$$
• escalando por 2 en todas las direcciones:$${\displaystyle \mathbf {A} ={\begin{pmatrix}2&0\\0&2\end{pmatrix}}=2\mathbf {I} }$$
• mapeo de cizallamiento horizontal :$${\displaystyle \mathbf {A} ={\begin{pmatrix}1&m\\0&1\end{pmatrix}}}$$
• inclinación del eje y en un ángulo θ :$${\displaystyle \mathbf {A} ={\begin{pmatrix}1&-\sin \theta \\0&\cos \theta \end{pmatrix}}}$$
• mapeo de compresión :$${\displaystyle \mathbf {A} ={\begin{pmatrix}k&0\\0&{\frac {1}{k}}\end{pmatrix}}}$$
• proyección sobre el eje y :$${\displaystyle \mathbf {A} ={\begin{pmatrix}0&0\\0&1\end{pmatrix}}.}$$

Si un mapa lineal solo se compone de rotación, reflexión y/o escala uniforme, entonces el mapa lineal es una transformación lineal conforme .

La composición de las aplicaciones lineales es lineal: si y son lineales, entonces también lo es su composición . De esto se sigue que la clase de todos los espacios vectoriales sobre un cuerpo dado K , junto con las aplicaciones K -lineales como morfismos , forma una categoría .${\displaystyle f:V\to W}$${\textstyle g:W\to Z}$ ${\textstyle g\circ f:V\to Z}$

La inversa de un mapa lineal, cuando se define, es nuevamente un mapa lineal.

Si y son lineales, entonces también lo es su suma puntual , que está definida por .${\textstyle f_{1}:V\to W}$${\textstyle f_{2}:V\to W}$${\displaystyle f_{1}+f_{2}}$${\displaystyle (f_{1}+f_{2})(\mathbf {x} )=f_{1}(\mathbf {x} )+f_{2}(\mathbf {x} )}$

Si es lineal y es un elemento del campo base , entonces el mapa , definido por , también es lineal.${\textstyle f:V\to W}$${\textstyle \alpha }$${\textstyle K}$${\textstyle \alpha f}$${\textstyle (\alpha f)(\mathbf {x} )=\alpha (f(\mathbf {x} ))}$

Así, el conjunto de aplicaciones lineales de a sí mismo forma un espacio vectorial sobre , ^[12] a veces denotado . ^[13] Además, en el caso de que , este espacio vectorial, denotado , es un álgebra asociativa bajo composición de aplicaciones , ya que la composición de dos aplicaciones lineales es nuevamente una aplicación lineal, y la composición de aplicaciones es siempre asociativa. Este caso se analiza con más detalle a continuación.${\textstyle {\mathcal {L}}(V,W)}$${\textstyle V}$${\textstyle W}$${\textstyle K}$${\textstyle \operatorname {Hom} (V,W)}$${\textstyle V=W}$${\textstyle \operatorname {End} (V)}$

Dado nuevamente el caso de dimensión finita, si se han elegido bases, entonces la composición de aplicaciones lineales corresponde a la multiplicación de matrices , la adición de aplicaciones lineales corresponde a la adición de matrices , y la multiplicación de aplicaciones lineales con escalares corresponde a la multiplicación de matrices con escalares.

Una transformación lineal es un endomorfismo de ; el conjunto de todos esos endomorfismos junto con la adición, la composición y la multiplicación escalar como se definió anteriormente forma un álgebra asociativa con elemento identidad sobre el cuerpo (y en particular un anillo ). El elemento identidad multiplicativo de esta álgebra es el mapa identidad .${\textstyle f:V\to V}$${\textstyle V}$${\textstyle \operatorname {End} (V)}$${\textstyle K}$ ${\textstyle \operatorname {id} :V\to V}$

Un endomorfismo de que es también un isomorfismo se llama automorfismo de . La composición de dos automorfismos es de nuevo un automorfismo, y el conjunto de todos los automorfismos de forma un grupo , cuyo grupo de automorfismos se denota por o . Puesto que los automorfismos son precisamente aquellos endomorfismos que poseen inversas bajo composición, es el grupo de unidades en el anillo .${\textstyle V}$${\textstyle V}$${\textstyle V}$${\textstyle V}$${\textstyle \operatorname {Aut} (V)}$${\textstyle \operatorname {GL} (V)}$${\textstyle \operatorname {Aut} (V)}$${\textstyle \operatorname {End} (V)}$

Si tiene dimensión finita , entonces es isomorfo al álgebra asociativa de todas las matrices con entradas en . El grupo de automorfismos de es isomorfo al grupo lineal general de todas las matrices invertibles con entradas en .${\textstyle V}$${\textstyle n}$${\textstyle \operatorname {End} (V)}$${\textstyle n\times n}$${\textstyle K}$${\textstyle V}$ ${\textstyle \operatorname {GL} (n,K)}$${\textstyle n\times n}$${\textstyle K}$

Si es lineal, definimos el núcleo y la imagen o rango de por${\textstyle f:V\to W}$${\textstyle f}$$${\displaystyle {\begin{aligned}\ker(f)&=\{\,\mathbf {x} \in V:f(\mathbf {x} )=\mathbf {0} \,\}\\\operatorname {im} (f)&=\{\,\mathbf {w} \in W:\mathbf {w} =f(\mathbf {x} ),\mathbf {x} \in V\,\}\end{aligned}}}$$

${\textstyle \ker(f)}$es un subespacio de y es un subespacio de . La siguiente fórmula de dimensión se conoce como teorema de rango-nulidad : ^[14]${\textstyle V}$${\textstyle \operatorname {im} (f)}$${\textstyle W}$$${\displaystyle \dim(\ker(f))+\dim(\operatorname {im} (f))=\dim(V).}$$

El número también se llama rango de y se escribe como , o a veces, ; ^{[15] [16]} el número se llama nulidad de y se escribe como o . ^{[15] [16]} Si y son de dimensión finita, se han elegido bases y está representado por la matriz , entonces el rango y la nulidad de son iguales al rango y la nulidad de la matriz , respectivamente.${\textstyle \dim(\operatorname {im} (f))}$${\textstyle f}$${\textstyle \operatorname {rank} (f)}$${\textstyle \rho (f)}$${\textstyle \dim(\ker(f))}$${\textstyle f}$${\textstyle \operatorname {null} (f)}$${\textstyle \nu (f)}$${\textstyle V}$${\textstyle W}$${\textstyle f}$${\textstyle A}$${\textstyle f}$${\textstyle A}$

Un invariante más sutil de una transformación lineal es el co- núcleo , que se define como${\textstyle f:V\to W}$$${\displaystyle \operatorname {coker} (f):=W/f(V)=W/\operatorname {im} (f).}$$

Esta es la noción dual del núcleo: así como el núcleo es un subespacio del dominio, el co-núcleo es un espacio cociente del objetivo. Formalmente, se tiene la secuencia exacta$${\displaystyle 0\to \ker(f)\to V\to W\to \operatorname {coker} (f)\to 0.}$$

Estos pueden interpretarse así: dada una ecuación lineal f ( v ) = w para resolver,

• el núcleo es el espacio de soluciones de la ecuación homogénea f ( v ) = 0, y su dimensión es el número de grados de libertad en el espacio de soluciones, si no está vacío;
• El co-núcleo es el espacio de restricciones que las soluciones deben satisfacer, y su dimensión es el número máximo de restricciones independientes.

La dimensión del co-núcleo y la dimensión de la imagen (el rango) se suman para dar la dimensión del espacio objetivo. Para dimensiones finitas, esto significa que la dimensión del espacio cociente W / f ( V ) es la dimensión del espacio objetivo menos la dimensión de la imagen.

Como ejemplo simple, considere la función f : R ² → R ² , dada por f ( x , y ) = (0, y ). Entonces, para que una ecuación f ( x , y ) = ( a , b ) tenga una solución, debemos tener a = 0 (una restricción), y en ese caso el espacio de solución es ( x , b ) o, expresado de manera equivalente, (0, b ) + ( x , 0), (un grado de libertad). El núcleo puede expresarse como el subespacio ( x , 0) < V : el valor de x es la libertad en una solución, mientras que el conúcleo puede expresarse mediante la función W → R , : dado un vector ( a , b ), el valor de a es la obstrucción para que haya una solución.${\textstyle (a,b)\mapsto (a)}$

Un ejemplo que ilustra el caso de dimensión infinita lo proporciona la función f : R ^∞ → R ^∞ , con b ₁ = 0 y b _{n + 1} = a _n para n > 0. Su imagen consiste en todas las secuencias con primer elemento 0, y por lo tanto su co-núcleo consiste en las clases de secuencias con primer elemento idéntico. Por lo tanto, mientras que su núcleo tiene dimensión 0 (solo asigna la secuencia cero a la secuencia cero), su co-núcleo tiene dimensión 1. Dado que el dominio y el espacio objetivo son los mismos, el rango y la dimensión del núcleo suman la misma suma que el rango y la dimensión del co-núcleo ( ), pero en el caso de dimensión infinita no se puede inferir que el núcleo y el co-núcleo de un endomorfismo tengan la misma dimensión (0 ≠ 1). La situación inversa se obtiene para la función h : R ^∞ → R ^∞ , con c _n = a _{n + 1} . Su imagen es todo el espacio objetivo y, por lo tanto, su co-núcleo tiene dimensión 0, pero como asigna todas las secuencias en las que solo el primer elemento no es cero a la secuencia cero, su núcleo tiene dimensión 1.${\textstyle \left\{a_{n}\right\}\mapsto \left\{b_{n}\right\}}$${\textstyle \aleph _{0}+0=\aleph _{0}+1}$${\textstyle \left\{a_{n}\right\}\mapsto \left\{c_{n}\right\}}$

Para un operador lineal con núcleo y co-núcleo de dimensión finita, se puede definir el índice como: es decir, los grados de libertad menos el número de restricciones.$${\displaystyle \operatorname {ind} (f):=\dim(\ker(f))-\dim(\operatorname {coker} (f)),}$$

Para una transformación entre espacios vectoriales de dimensión finita, esta es simplemente la diferencia dim( V ) − dim( W ), por rango–nulidad. Esto da una indicación de cuántas soluciones o cuántas restricciones uno tiene: si se aplica un mapeo de un espacio más grande a uno más pequeño, el mapeo puede ser sobreyectivo y, por lo tanto, tendrá grados de libertad incluso sin restricciones. Por el contrario, si se aplica un mapeo de un espacio más pequeño a uno más grande, el mapeo no puede ser sobreyectivo y, por lo tanto, uno tendrá restricciones incluso sin grados de libertad.

El índice de un operador es precisamente la característica de Euler del complejo de 2 términos 0 → V → W → 0. En la teoría de operadores , el índice de los operadores de Fredholm es un objeto de estudio, siendo un resultado importante el teorema del índice de Atiyah-Singer . ^[17]

Ninguna clasificación de aplicaciones lineales podría ser exhaustiva. La siguiente lista incompleta enumera algunas clasificaciones importantes que no requieren ninguna estructura adicional en el espacio vectorial.

Sean V y W espacios vectoriales sobre un cuerpo F y sea T : V → W una función lineal.

Se dice que T es inyectiva o un monomorfismo si se cumple alguna de las siguientes condiciones equivalentes:

1. T es uno a uno como un mapa de conjuntos .
2. voltaje T = {0 _V }
3. atenuación(ker T ) = 0
4. T es mónico o cancelable por la izquierda, es decir, para cualquier espacio vectorial U y cualquier par de aplicaciones lineales R : U → V y S : U → V , la ecuación TR = TS implica R = S .
5. T es invertible por la izquierda , lo que significa que existe una función lineal S : W → V tal que ST es la función identidad en V .

Se dice que T es sobreyectiva o un epimorfismo si se cumple alguna de las siguientes condiciones equivalentes:

1. T es sobre un mapa de conjuntos.
2. coquizador T = {0 _W }
3. T es épico o cancelable por la derecha, es decir, para cualquier espacio vectorial U y cualquier par de aplicaciones lineales R : W → U y S : W → U , la ecuación RT = ST implica R = S .
4. T es invertible por la derecha , lo que significa que existe una función lineal S : W → V tal que TS es la función identidad en W .

Se dice que T es un isomorfismo si es invertible tanto por la izquierda como por la derecha. Esto es equivalente a que T sea tanto uno a uno como sobre (una biyección de conjuntos) o también a que T sea tanto épico como mónico, y por lo tanto un bimorfismo .

Si T : V → V es un endomorfismo, entonces:

• Si, para algún entero positivo n , el n -ésimo iterado de T , T ⁿ , es idénticamente cero, entonces se dice que T es nilpotente .
• Si T ² = T , entonces se dice que T es idempotente
• Si T = kI , donde k es algún escalar, entonces se dice que T es una transformación de escala o un mapa de multiplicación escalar; véase matriz escalar .

Dada una función lineal que es un endomorfismo cuya matriz es A , en la base B del espacio transforma las coordenadas del vector [u] como [v] = A [u]. Como los vectores cambian con la inversa de B (las coordenadas de los vectores son contravariantes ) su transformación inversa es [v] = B [v'].

Sustituyendo esto en la primera expresión por lo tanto$${\displaystyle B\left[v'\right]=AB\left[u'\right]}$$$${\displaystyle \left[v'\right]=B^{-1}AB\left[u'\right]=A'\left[u'\right].}$$

Por lo tanto, la matriz en la nueva base es A′ = B ⁻¹ AB , siendo B la matriz de la base dada.

Por lo tanto, se dice que los mapas lineales son objetos 1-co- 1-contra- variantes , o tensores de tipo (1, 1) .

Una transformación lineal entre espacios vectoriales topológicos , por ejemplo espacios normados , puede ser continua . Si su dominio y codominio son los mismos, entonces será un operador lineal continuo . Un operador lineal en un espacio lineal normado es continuo si y solo si está acotado , por ejemplo, cuando el dominio es de dimensión finita. ^[18] Un dominio de dimensión infinita puede tener operadores lineales discontinuos .

Un ejemplo de una transformación lineal no acotada, y por lo tanto discontinua, es la diferenciación en el espacio de funciones suaves dotadas de la norma suprema (una función con valores pequeños puede tener una derivada con valores grandes, mientras que la derivada de 0 es 0). Para un ejemplo específico, sin( nx )/ n converge a 0, pero su derivada cos( nx ) no, por lo que la diferenciación no es continua en 0 (y mediante una variación de este argumento, no es continua en ninguna parte).

Una aplicación específica de los mapas lineales es para las transformaciones geométricas , como las que se realizan en gráficos de computadora , donde la traslación, rotación y escala de objetos 2D o 3D se realiza mediante el uso de una matriz de transformación . Los mapas lineales también se utilizan como un mecanismo para describir el cambio: por ejemplo, en cálculo corresponden a derivadas; o en relatividad, se utilizan como un dispositivo para realizar un seguimiento de las transformaciones locales de los marcos de referencia.

Otra aplicación de estas transformaciones es en las optimizaciones del compilador de código de bucle anidado y en la paralelización de técnicas de compilación .

Wikilibros tiene un libro sobre el tema: Álgebra lineal/Transformaciones lineales

• Mapa aditivo  – homomorfismo del módulo Z
• Mapa antilineal  – Mapa aditivo homogéneo conjugado
• Función Bent  : tipo especial de función booleana
• Operador acotado  : transformación lineal entre espacios vectoriales topológicos
• Ecuación funcional de Cauchy  – Ecuación funcional
• Operador lineal continuo
• Funcional lineal  : Mapa lineal de un espacio vectorial a su campo de escalaresPages displaying short descriptions of redirect targets
• Isometría lineal  : transformación matemática que preserva la distanciaPages displaying short descriptions of redirect targets
• Categoría de matrices
• Cuasilinealización

• Axler, Sheldon Jay (2015). Álgebra lineal bien hecha (3.ª ed.). Springer . ISBN 978-3-319-11079-0.
• Bronshtein, IN; Semendyayev, KA (2004). Manual de matemáticas (4.ª ed.). Nueva York: Springer-Verlag. ISBN 3-540-43491-7.
• Halmos, Paul Richard (1974) [1958]. Espacios vectoriales de dimensión finita (2.ª ed.). Springer . ISBN 0-387-90093-4.
• Horn, Roger A.; Johnson, Charles R. (2013). Análisis de matrices (segunda edición). Cambridge University Press . ISBN 978-0-521-83940-2.
• Katznelson, Yitzhak ; Katznelson, Yonatan R. (2008). Una introducción (concisa) al álgebra lineal . Sociedad Matemática Estadounidense . ISBN 978-0-8218-4419-9.
• Kubrusly, Carlos (2001). Elementos de teoría de operadores . Boston: Birkhäuser. ISBN 978-1-4757-3328-0.OCLC 754555941  .
• Lang, Serge (1987), Álgebra lineal (tercera edición), Nueva York: Springer-Verlag , ISBN 0-387-96412-6
• Rudin, Walter (1973). Análisis funcional . Serie internacional de matemáticas puras y aplicadas. Vol. 25 (primera edición). Nueva York, NY: McGraw-Hill Science/Engineering/Math . ISBN 9780070542259.
• Rudin, Walter (1976). Principios del análisis matemático. Walter Rudin Student Series in Advanced Mathematics (3.ª ed.). Nueva York: McGraw–Hill. ISBN 978-0-07-054235-8.
• Rudin, Walter (1991). Análisis funcional. Serie internacional de matemáticas puras y aplicadas. Vol. 8 (segunda edición). Nueva York, NY: McGraw-Hill Science/Engineering/Math . ISBN 978-0-07-054236-5.OCLC 21163277  .
• Schaefer, Helmut H. ; Wolff, Manfred P. (1999). Espacios vectoriales topológicos . GTM . Vol. 8 (Segunda ed.). Nueva York, NY: Springer New York Imprenta Springer. ISBN 978-1-4612-7155-0.OCLC 840278135  .
• Schechter, Eric (1996). Manual de análisis y sus fundamentos . San Diego, CA: Academic Press. ISBN 978-0-12-622760-4.OCLC 175294365  .
• Swartz, Charles (1992). Introducción al análisis funcional . Nueva York: M. Dekker. ISBN 978-0-8247-8643-4.OCLC 24909067  .
• Tu, Loring W. (2011). Introducción a las variedades (2.ª ed.). Springer . ISBN 978-0-8218-4419-9.
• Wilansky, Albert (2013). Métodos modernos en espacios vectoriales topológicos . Mineola, Nueva York: Dover Publications, Inc. ISBN 978-0-486-49353-4.OCLC 849801114  .