Fuerza
| Fuerza | |
|---|---|
 Las fuerzas pueden describirse como un empuje o un tirón sobre un objeto. Pueden deberse a fenómenos como la gravedad , el magnetismo o cualquier cosa que pueda hacer que una masa se acelere. | |
Símbolos comunes | , yo , yo |
| Unidad SI | Newton (N) |
Otras unidades | dina , libra-fuerza , poundal , kip , kilopondio |
| En unidades base del SI | kg · m · s −2 |
Derivaciones de otras magnitudes | F = m a |
| Dimensión | |
| Parte de una serie sobre |
| Mecánica clásica |
|---|
Una fuerza es una influencia que puede hacer que un objeto cambie su velocidad a menos que se contrarreste con otras fuerzas. El concepto de fuerza hace que la noción cotidiana de empujar o tirar sea matemáticamente precisa. Debido a que tanto la magnitud como la dirección de una fuerza son importantes, la fuerza es una cantidad vectorial . La unidad de fuerza del SI es el newton (N) y la fuerza se representa a menudo con el símbolo F.
La fuerza juega un papel importante en la mecánica clásica. El concepto de fuerza es central para las tres leyes de movimiento de Newton . Los tipos de fuerzas que se encuentran a menudo en la mecánica clásica incluyen las fuerzas elásticas , de fricción , de contacto o "normales" y gravitacionales . La versión rotacional de la fuerza es el torque , que produce cambios en la velocidad rotacional de un objeto. En un cuerpo extenso, cada parte a menudo aplica fuerzas sobre las partes adyacentes; la distribución de tales fuerzas a través del cuerpo es la tensión mecánica interna . En equilibrio, estas tensiones no causan aceleración del cuerpo ya que las fuerzas se equilibran entre sí. Si estas no están en equilibrio, pueden causar deformación de materiales sólidos o flujo en fluidos .
En la física moderna , que incluye la relatividad y la mecánica cuántica , las leyes que rigen el movimiento se revisan para basarse en interacciones fundamentales como el origen último de la fuerza. Sin embargo, la comprensión de la fuerza proporcionada por la mecánica clásica es útil para fines prácticos. [1]
Desarrollo del concepto
Los filósofos de la antigüedad utilizaban el concepto de fuerza en el estudio de objetos estacionarios y móviles y máquinas simples , pero pensadores como Aristóteles y Arquímedes mantuvieron errores fundamentales en la comprensión de la fuerza. En parte, esto se debió a una comprensión incompleta de la fuerza de fricción, a veces no obvia, y una visión consecuentemente inadecuada de la naturaleza del movimiento natural. [2] Un error fundamental fue la creencia de que se requiere una fuerza para mantener el movimiento, incluso a una velocidad constante. La mayoría de los malentendidos anteriores sobre el movimiento y la fuerza fueron finalmente corregidos por Galileo Galilei y Sir Isaac Newton . Con su visión matemática, Newton formuló leyes del movimiento que no se mejoraron durante más de doscientos años. [3]
A principios del siglo XX, Einstein desarrolló una teoría de la relatividad que predijo correctamente la acción de fuerzas sobre objetos con momentos crecientes cerca de la velocidad de la luz y también proporcionó información sobre las fuerzas producidas por la gravitación y la inercia . Con los conocimientos modernos sobre la mecánica cuántica y la tecnología que puede acelerar partículas cerca de la velocidad de la luz, la física de partículas ha ideado un Modelo Estándar para describir las fuerzas entre partículas más pequeñas que los átomos. El Modelo Estándar predice que las partículas intercambiadas llamadas bosones de calibre son el medio fundamental por el cual se emiten y absorben las fuerzas. Solo se conocen cuatro interacciones principales: en orden de fuerza decreciente, son: fuerte , electromagnética , débil y gravitacional . [4] : 2–10 [5] : 79 Las observaciones de física de partículas de alta energía realizadas durante los años 1970 y 1980 confirmaron que las fuerzas débil y electromagnética son expresiones de una interacción electrodébil más fundamental . [6]
Conceptos prenewtonianos

Desde la antigüedad, el concepto de fuerza ha sido reconocido como parte integral del funcionamiento de cada una de las máquinas simples . La ventaja mecánica que brinda una máquina simple permitía utilizar menos fuerza a cambio de que esa fuerza actuara sobre una distancia mayor para la misma cantidad de trabajo . El análisis de las características de las fuerzas culminó finalmente en el trabajo de Arquímedes , quien fue especialmente famoso por formular un tratamiento de las fuerzas de flotación inherentes a los fluidos . [2]
Aristóteles proporcionó una discusión filosófica del concepto de fuerza como parte integral de la cosmología aristotélica . En la visión de Aristóteles, la esfera terrestre contenía cuatro elementos que se detenían en diferentes "lugares naturales" en ella. Aristóteles creía que los objetos inmóviles en la Tierra, aquellos compuestos principalmente por los elementos tierra y agua, estaban en su lugar natural cuando estaban en el suelo, y que permanecían así si se los dejaba solos. Distinguió entre la tendencia innata de los objetos a encontrar su "lugar natural" (por ejemplo, que los cuerpos pesados caigan), lo que conduce al "movimiento natural", y el movimiento no natural o forzado, que requiere la aplicación continua de una fuerza. [7] Esta teoría, basada en la experiencia cotidiana de cómo se mueven los objetos, como la aplicación constante de una fuerza necesaria para mantener un carro en movimiento, tenía problemas conceptuales para explicar el comportamiento de los proyectiles , como el vuelo de las flechas. Un arquero hace que la flecha se mueva al comienzo del vuelo, y luego vuela por el aire aunque no actúe sobre ella ninguna causa eficiente discernible. Aristóteles era consciente de este problema y propuso que el aire desplazado a lo largo de la trayectoria del proyectil lo lleva hasta su objetivo. Esta explicación requiere un medio continuo como el aire para mantener el movimiento. [8]
Aunque la física aristotélica fue criticada ya en el siglo VI, [9] [10] sus deficiencias no se corregirían hasta el trabajo del siglo XVII de Galileo Galilei , quien fue influenciado por la idea de finales de la Edad Media de que los objetos en movimiento forzado tenían una fuerza innata de impulso . Galileo construyó un experimento en el que se hicieron rodar piedras y balas de cañón por una pendiente para refutar la teoría aristotélica del movimiento . Demostró que los cuerpos eran acelerados por la gravedad en una medida que era independiente de su masa y argumentó que los objetos conservan su velocidad a menos que actúe sobre ellos una fuerza, por ejemplo la fricción . [11] La idea de Galileo de que se necesita fuerza para cambiar el movimiento en lugar de mantenerlo, mejorada aún más por Isaac Beeckman , René Descartes y Pierre Gassendi , se convirtió en un principio clave de la física newtoniana. [12]
A principios del siglo XVII, antes de los Principia de Newton , el término «fuerza» ( en latín : vis ) se aplicaba a muchos fenómenos físicos y no físicos, por ejemplo, a la aceleración de un punto. El producto de la masa de un punto por el cuadrado de su velocidad fue denominado vis viva (fuerza viva) por Leibniz . El concepto moderno de fuerza corresponde a la vis motrix (fuerza de aceleración) de Newton. [13]
Mecánica newtoniana
Sir Isaac Newton describió el movimiento de todos los objetos utilizando los conceptos de inercia y fuerza. En 1687, Newton publicó su obra magna, Philosophiæ Naturalis Principia Mathematica . [3] [14] En esta obra, Newton estableció tres leyes del movimiento que han dominado la forma en que se describen las fuerzas en física hasta el día de hoy. [14] Las formas precisas en que se expresan las leyes de Newton han evolucionado al ritmo de los nuevos enfoques matemáticos. [15]
Primera ley
La primera ley del movimiento de Newton establece que el comportamiento natural de un objeto en reposo es continuar estando en reposo, y el comportamiento natural de un objeto que se mueve a velocidad constante en línea recta es continuar moviéndose a esa velocidad constante a lo largo de esa línea recta. [14] Esto último se desprende de lo primero debido al principio de que las leyes de la física son las mismas para todos los observadores inerciales , es decir, todos los observadores que no se sienten en movimiento. Un observador que se mueve en tándem con un objeto lo verá como si estuviera en reposo. Por lo tanto, su comportamiento natural será permanecer en reposo con respecto a ese observador, lo que significa que un observador que lo vea moverse a velocidad constante en línea recta verá que continúa haciéndolo. [16] : 1–7

Segunda ley
Según la primera ley, el movimiento a velocidad constante en línea recta no necesita una causa. Es el cambio en el movimiento lo que requiere una causa, y la segunda ley de Newton proporciona la relación cuantitativa entre fuerza y cambio de movimiento. La segunda ley de Newton establece que la fuerza neta que actúa sobre un objeto es igual a la tasa a la que su momento cambia con el tiempo . Si la masa del objeto es constante, esta ley implica que la aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre el objeto, está en la dirección de la fuerza neta y es inversamente proporcional a la masa del objeto. [17] : 204–207
Una formulación moderna de la segunda ley de Newton es una ecuación vectorial: F = d p d t , {\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}},} donde es el momento del sistema, y es la fuerza neta ( suma vectorial ). [17] : 399 Si un cuerpo está en equilibrio, por definición no hay fuerza neta (pueden estar presentes fuerzas equilibradas de todos modos). Por el contrario, la segunda ley establece que si hay una fuerza desequilibrada actuando sobre un objeto, esto provocará que el momento del objeto cambie con el tiempo. [14]
En aplicaciones de ingeniería comunes, la masa en un sistema permanece constante, lo que permite una forma algebraica simple para la segunda ley. Por la definición de momento, donde m es la masa y es la velocidad . [4] : 9-1,9-2 Si la segunda ley de Newton se aplica a un sistema de masa constante , m puede moverse fuera del operador derivada. La ecuación entonces se convierte en Al sustituir la definición de aceleración , se deriva la versión algebraica de la segunda ley de Newton : F = m a . {\displaystyle \mathbf {F} =m\mathbf {a} .}
Tercera ley
Siempre que un cuerpo ejerce una fuerza sobre otro, este último ejerce simultáneamente una fuerza igual y opuesta sobre el primero. En forma vectorial, si es la fuerza del cuerpo 1 sobre el cuerpo 2 y la del cuerpo 2 sobre el cuerpo 1, entonces Esta ley a veces se denomina ley de acción-reacción , y se denomina acción y reacción .
La tercera ley de Newton es el resultado de aplicar la simetría a situaciones en las que las fuerzas pueden atribuirse a la presencia de diferentes objetos. La tercera ley significa que todas las fuerzas son interacciones entre diferentes cuerpos. [18] [19] y, por lo tanto, no existe una fuerza unidireccional o una fuerza que actúe sobre un solo cuerpo.
En un sistema compuesto por el objeto 1 y el objeto 2, la fuerza neta sobre el sistema debido a sus interacciones mutuas es cero: En términos más generales, en un sistema cerrado de partículas, todas las fuerzas internas están equilibradas. Las partículas pueden acelerarse entre sí, pero el centro de masas del sistema no lo hará. Si una fuerza externa actúa sobre el sistema, hará que el centro de masas se acelere en proporción a la magnitud de la fuerza externa dividida por la masa del sistema. [4] : 19-1 [5]
Combinando la segunda y tercera ley de Newton, es posible demostrar que el momento lineal de un sistema se conserva en cualquier sistema cerrado . En un sistema de dos partículas, si es el momento del objeto 1 y el momento del objeto 2, entonces Utilizando argumentos similares, esto se puede generalizar a un sistema con un número arbitrario de partículas. En general, siempre que todas las fuerzas se deban a la interacción de objetos con masa, es posible definir un sistema tal que el momento neto nunca se pierda ni se gane. [4] : cap.12 [5]
Definición de "fuerza"
Algunos libros de texto utilizan la segunda ley de Newton como definición de fuerza. [20] [21] [22] [23] Sin embargo, para que la ecuación para una masa constante tenga algún contenido predictivo, debe combinarse con información adicional. [24] [4] : 12-1 Además, inferir que una fuerza está presente porque un cuerpo está acelerando solo es válido en un marco de referencia inercial. [5] : 59 La pregunta de qué aspectos de las leyes de Newton tomar como definiciones y cuáles considerar como que tienen contenido físico ha sido respondida de varias maneras, [25] [26] : vii que en última instancia no afectan cómo se usa la teoría en la práctica. [25] Entre los físicos, filósofos y matemáticos notables que han buscado una definición más explícita del concepto de fuerza se incluyen Ernst Mach y Walter Noll . [27] [28]
Combinando fuerzas

Las fuerzas actúan en una dirección particular y tienen magnitudes que dependen de qué tan fuerte sea el empuje o la atracción. Debido a estas características, las fuerzas se clasifican como " magnitudes vectoriales ". Esto significa que las fuerzas siguen un conjunto diferente de reglas matemáticas que las magnitudes físicas que no tienen dirección (denominadas magnitudes escalares ). Por ejemplo, al determinar qué sucede cuando dos fuerzas actúan sobre el mismo objeto, es necesario conocer tanto la magnitud como la dirección de ambas fuerzas para calcular el resultado . Si no se conocen ambos datos para cada fuerza, la situación es ambigua. [17] : 197
Históricamente, las fuerzas se investigaron cuantitativamente por primera vez en condiciones de equilibrio estático donde varias fuerzas se cancelaban entre sí. Tales experimentos demuestran las propiedades cruciales de que las fuerzas son cantidades vectoriales aditivas : tienen magnitud y dirección. [3] Cuando dos fuerzas actúan sobre una partícula puntual , la fuerza resultante ( también llamada fuerza neta ), se puede determinar siguiendo la regla del paralelogramo de la adición de vectores : la suma de dos vectores representados por los lados de un paralelogramo da un vector resultante equivalente que es igual en magnitud y dirección a la transversal del paralelogramo. La magnitud de la resultante varía desde la diferencia de las magnitudes de las dos fuerzas hasta su suma, dependiendo del ángulo entre sus líneas de acción. [4] : cap.12 [5]
Los diagramas de cuerpo libre se pueden utilizar como una forma conveniente de llevar un registro de las fuerzas que actúan sobre un sistema. Lo ideal es que estos diagramas se dibujen conservando los ángulos y las magnitudes relativas de los vectores de fuerza, de modo que se pueda realizar una suma gráfica de vectores para determinar la fuerza neta. [29]
Además de sumarse, las fuerzas también se pueden descomponer en componentes independientes en ángulos rectos entre sí. Por lo tanto, una fuerza horizontal que apunta al noreste se puede dividir en dos fuerzas, una que apunta al norte y otra que apunta al este. Sumando estas fuerzas componentes mediante la suma de vectores se obtiene la fuerza original. Resolver los vectores de fuerza en componentes de un conjunto de vectores base es a menudo una forma matemáticamente más clara de describir fuerzas que usar magnitudes y direcciones. [30] Esto se debe a que, para los componentes ortogonales , los componentes de la suma vectorial se determinan de forma única mediante la suma escalar de los componentes de los vectores individuales. Los componentes ortogonales son independientes entre sí porque las fuerzas que actúan a noventa grados entre sí no tienen efecto sobre la magnitud o la dirección del otro. La elección de un conjunto de vectores base ortogonales se realiza a menudo considerando qué conjunto de vectores base hará que las matemáticas sean más convenientes. Es deseable elegir un vector base que esté en la misma dirección que una de las fuerzas, ya que esa fuerza tendría entonces solo un componente distinto de cero. Los vectores de fuerza ortogonales pueden ser tridimensionales y el tercer componente está en ángulo recto con los otros dos. [4] : cap.12 [5]
Equilibrio
Cuando todas las fuerzas que actúan sobre un objeto están equilibradas, se dice que el objeto está en un estado de equilibrio . [17] : 566 Por lo tanto, el equilibrio se produce cuando la fuerza resultante que actúa sobre una partícula puntual es cero (es decir, la suma vectorial de todas las fuerzas es cero). Cuando se trata de un cuerpo extenso, también es necesario que el par neto sea cero. Un cuerpo está en equilibrio estático con respecto a un marco de referencia si está en reposo y no acelera, mientras que un cuerpo en equilibrio dinámico se mueve a una velocidad constante en línea recta, es decir, se mueve pero no acelera. Lo que un observador ve como equilibrio estático, otro puede verlo como equilibrio dinámico y viceversa. [17] : 566
Estático
El equilibrio estático se conocía mucho antes de la invención de la mecánica clásica. Los objetos que no se aceleran sufren una fuerza neta nula. [31]
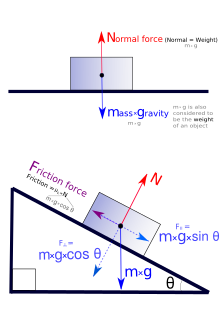
El caso más simple de equilibrio estático se produce cuando dos fuerzas son iguales en magnitud pero opuestas en dirección. Por ejemplo, un objeto que se encuentra sobre una superficie plana es atraído hacia abajo, en dirección al centro de la Tierra, por la fuerza de la gravedad. Al mismo tiempo, la superficie aplica una fuerza que resiste la fuerza hacia abajo con una fuerza hacia arriba igual (llamada fuerza normal ). La situación produce una fuerza neta cero y, por lo tanto, ninguna aceleración. [3]
Al empujar un objeto que reposa sobre una superficie de fricción, se puede producir una situación en la que el objeto no se mueve porque la fuerza aplicada se opone a la fricción estática , generada entre el objeto y la superficie de la mesa. En una situación sin movimiento, la fuerza de fricción estática equilibra exactamente la fuerza aplicada, lo que da como resultado que no haya aceleración. La fricción estática aumenta o disminuye en respuesta a la fuerza aplicada hasta un límite superior determinado por las características del contacto entre la superficie y el objeto. [3]
El equilibrio estático entre dos fuerzas es la forma más habitual de medir fuerzas, utilizando dispositivos simples como básculas y balanzas de resorte . Por ejemplo, un objeto suspendido en una báscula de resorte vertical experimenta la fuerza de gravedad que actúa sobre el objeto equilibrado por una fuerza aplicada por la "fuerza de reacción del resorte", que es igual al peso del objeto. Utilizando tales herramientas, se descubrieron algunas leyes de fuerza cuantitativas: que la fuerza de gravedad es proporcional al volumen para objetos de densidad constante (ampliamente explotada durante milenios para definir pesos estándar); el principio de Arquímedes para la flotabilidad; el análisis de Arquímedes de la palanca ; la ley de Boyle para la presión de los gases; y la ley de Hooke para los resortes. Todas estas leyes fueron formuladas y verificadas experimentalmente antes de que Isaac Newton expusiera sus Tres leyes del movimiento . [3] [4] : cap.12 [5]
Dinámica

El equilibrio dinámico fue descrito por primera vez por Galileo, quien se dio cuenta de que ciertas suposiciones de la física aristotélica eran contradichas por las observaciones y la lógica . Galileo se dio cuenta de que la simple suma de velocidades exige que el concepto de un " marco de reposo absoluto " no exista. Galileo concluyó que el movimiento a una velocidad constante era completamente equivalente al reposo. Esto era contrario a la noción de Aristóteles de un "estado natural" de reposo al que los objetos con masa se aproximan naturalmente. Experimentos simples mostraron que la comprensión de Galileo de la equivalencia de la velocidad constante y el reposo era correcta. Por ejemplo, si un marinero dejaba caer una bala de cañón desde el nido de vigía de un barco que se movía a una velocidad constante, la física aristotélica haría que la bala de cañón cayera directamente hacia abajo mientras el barco se movía debajo de ella. Por lo tanto, en un universo aristotélico, la bala de cañón que cae aterrizaría detrás del pie del mástil de un barco en movimiento. Cuando este experimento se lleva a cabo realmente, la bala de cañón siempre cae al pie del mástil, como si la bala de cañón supiera viajar con el barco a pesar de estar separada de él. Como no se aplica ninguna fuerza horizontal hacia adelante sobre la bala de cañón mientras cae, la única conclusión que queda es que la bala de cañón continúa moviéndose con la misma velocidad que el barco mientras cae. Por lo tanto, no se requiere ninguna fuerza para mantener la bala de cañón en movimiento a la velocidad de avance constante. [11]
Además, cualquier objeto que se desplace a una velocidad constante debe estar sujeto a una fuerza neta cero (fuerza resultante). Esta es la definición de equilibrio dinámico: cuando todas las fuerzas sobre un objeto se equilibran pero aún se mueve a una velocidad constante. Un caso simple de equilibrio dinámico ocurre en un movimiento a velocidad constante a través de una superficie con fricción cinética . En tal situación, se aplica una fuerza en la dirección del movimiento mientras que la fuerza de fricción cinética se opone exactamente a la fuerza aplicada. Esto da como resultado una fuerza neta cero, pero como el objeto comenzó con una velocidad distinta de cero, continúa moviéndose con una velocidad distinta de cero. Aristóteles interpretó erróneamente este movimiento como causado por la fuerza aplicada. Cuando se toma en cuenta la fricción cinética, está claro que no hay una fuerza neta que cause el movimiento a velocidad constante. [4] : cap.12 [5]
Ejemplos de fuerzas en la mecánica clásica
Algunas fuerzas son consecuencia de las fundamentales. En tales situaciones, se pueden utilizar modelos idealizados para obtener información física. Por ejemplo, cada objeto sólido se considera un cuerpo rígido . [ cita requerida ]
Fuerza gravitacional o gravedad

Lo que ahora llamamos gravedad no fue identificado como una fuerza universal hasta el trabajo de Isaac Newton. Antes de Newton, no se entendía que la tendencia de los objetos a caer hacia la Tierra estuviera relacionada con los movimientos de los objetos celestes. Galileo fue fundamental en la descripción de las características de los objetos que caen al determinar que la aceleración de cada objeto en caída libre era constante e independiente de la masa del objeto. Hoy en día, esta aceleración debida a la gravedad hacia la superficie de la Tierra se suele designar como y tiene una magnitud de aproximadamente 9,81 metros por segundo al cuadrado (esta medida se toma desde el nivel del mar y puede variar según la ubicación), y apunta hacia el centro de la Tierra. [32] Esta observación significa que la fuerza de gravedad sobre un objeto en la superficie de la Tierra es directamente proporcional a la masa del objeto. Por lo tanto, un objeto que tiene una masa de experimentará una fuerza:
En el caso de un objeto en caída libre, esta fuerza no tiene oposición y la fuerza neta sobre el objeto es su peso. En el caso de los objetos que no están en caída libre, la fuerza de gravedad se opone a las fuerzas de reacción aplicadas por sus soportes. Por ejemplo, una persona parada en el suelo experimenta una fuerza neta cero, ya que el suelo ejerce una fuerza normal (una fuerza de reacción) hacia arriba sobre la persona que contrarresta su peso dirigido hacia abajo. [4] : cap.12 [5]
La contribución de Newton a la teoría gravitacional fue unificar los movimientos de los cuerpos celestes, que Aristóteles había asumido que se encontraban en un estado natural de movimiento constante, con el movimiento de caída observado en la Tierra. Propuso una ley de la gravedad que podría explicar los movimientos celestes que se habían descrito anteriormente utilizando las leyes de Kepler del movimiento planetario . [33]
Newton se dio cuenta de que los efectos de la gravedad se podían observar de diferentes maneras a distancias mayores. En particular, Newton determinó que la aceleración de la Luna alrededor de la Tierra podía atribuirse a la misma fuerza de gravedad si la aceleración debida a la gravedad disminuía como una ley del cuadrado inverso . Además, Newton se dio cuenta de que la aceleración de un cuerpo debido a la gravedad es proporcional a la masa del otro cuerpo que lo atrae. [33] La combinación de estas ideas da una fórmula que relaciona la masa ( ) y el radio ( ) de la Tierra con la aceleración gravitacional: g = − G m ⊕ R ⊕ 2 r ^ , {\displaystyle \mathbf {g} =-{\frac {Gm_{\oplus }}{{R_{\oplus }}^{2}}}{\hat {\mathbf {r} }},} donde la dirección del vector está dada por , es el vector unitario dirigido hacia afuera desde el centro de la Tierra. [14]
En esta ecuación, se utiliza una constante dimensional para describir la fuerza relativa de la gravedad. Esta constante ha llegado a conocerse como la constante de gravitación newtoniana , aunque su valor era desconocido en vida de Newton. No fue hasta 1798 que Henry Cavendish pudo hacer la primera medición de la gravedad utilizando una balanza de torsión ; esto fue ampliamente reportado en la prensa como una medición de la masa de la Tierra, ya que conocerla podía permitir resolver la masa de la Tierra dada la ecuación anterior. Newton se dio cuenta de que, dado que todos los cuerpos celestes seguían las mismas leyes de movimiento , su ley de la gravedad tenía que ser universal. En pocas palabras, la ley de gravitación de Newton establece que la fuerza sobre un objeto esférico de masa debido a la atracción gravitatoria de la masa es F = − G m 1 m 2 r 2 r ^ , {\displaystyle \mathbf {F} =-{\frac {Gm_{1}m_{2}}{r^{2}}}{\hat {\mathbf {r} }},} donde es la distancia entre los centros de masa de los dos objetos y es el vector unitario que apunta en la dirección que se aleja del centro del primer objeto hacia el centro del segundo objeto. [14]
Esta fórmula fue lo suficientemente poderosa como para servir de base para todas las descripciones posteriores del movimiento dentro del sistema solar hasta el siglo XX. Durante ese tiempo, se inventaron métodos sofisticados de análisis de perturbaciones [34] para calcular las desviaciones de las órbitas debido a la influencia de múltiples cuerpos en un planeta , luna , cometa o asteroide . El formalismo fue lo suficientemente exacto como para permitir a los matemáticos predecir la existencia del planeta Neptuno antes de que fuera observado. [35]
Electromagnético
La fuerza electrostática fue descrita por primera vez en 1784 por Coulomb como una fuerza que existía intrínsecamente entre dos cargas . [36] : 519 Las propiedades de la fuerza electrostática eran que variaba como una ley del cuadrado inverso dirigida en la dirección radial , era tanto atractiva como repulsiva (había polaridad intrínseca ), era independiente de la masa de los objetos cargados y seguía el principio de superposición . La ley de Coulomb unifica todas estas observaciones en una declaración sucinta. [37]
Matemáticos y físicos posteriores encontraron que la construcción del campo eléctrico era útil para determinar la fuerza electrostática sobre una carga eléctrica en cualquier punto del espacio. El campo eléctrico se basó en el uso de una " carga de prueba " hipotética en cualquier lugar del espacio y luego usar la Ley de Coulomb para determinar la fuerza electrostática. [38] : 4-6–4-8 Por lo tanto, el campo eléctrico en cualquier lugar del espacio se define como donde es la magnitud de la carga de prueba hipotética. De manera similar, se introdujo la idea del campo magnético para expresar cómo los imanes pueden influenciarse entre sí a distancia. La ley de fuerza de Lorentz da la fuerza sobre un cuerpo con carga debido a los campos eléctrico y magnético: F = q ( E + v × B ) , {\displaystyle \mathbf {F} =q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),} donde es la fuerza electromagnética, es el campo eléctrico en la ubicación del cuerpo, es el campo magnético y es la velocidad de la partícula. La contribución magnética a la fuerza de Lorentz es el producto vectorial del vector de velocidad por el campo magnético. [39] [40] : 482
El origen de los campos eléctricos y magnéticos no se explicaría completamente hasta 1864, cuando James Clerk Maxwell unificó varias teorías anteriores en un conjunto de 20 ecuaciones escalares, que luego fueron reformuladas en 4 ecuaciones vectoriales por Oliver Heaviside y Josiah Willard Gibbs . [41] Estas " ecuaciones de Maxwell " describían completamente las fuentes de los campos como cargas estacionarias y en movimiento, y las interacciones de los propios campos. Esto llevó a Maxwell a descubrir que los campos eléctricos y magnéticos podían ser "autogenerados" a través de una onda que viajaba a una velocidad que él calculó que era la velocidad de la luz . Esta idea unió los campos nacientes de la teoría electromagnética con la óptica y condujo directamente a una descripción completa del espectro electromagnético . [42]
Normal

Cuando los objetos están en contacto, la fuerza que se ejerce directamente entre ellos se denomina fuerza normal, el componente de la fuerza total en el sistema ejercida de manera normal a la interfaz entre los objetos. [36] : 264 La fuerza normal está estrechamente relacionada con la tercera ley de Newton. La fuerza normal, por ejemplo, es responsable de la integridad estructural de mesas y pisos, además de ser la fuerza que responde siempre que una fuerza externa empuja un objeto sólido. Un ejemplo de la fuerza normal en acción es la fuerza de impacto sobre un objeto que choca contra una superficie inmóvil. [4] : cap.12 [5]
Fricción
La fricción es una fuerza que se opone al movimiento relativo de dos cuerpos. A escala macroscópica, la fuerza de fricción está directamente relacionada con la fuerza normal en el punto de contacto. Existen dos grandes clasificaciones de fuerzas de fricción: fricción estática y fricción cinética . [17] : 267
La fuerza de fricción estática ( ) se opondrá exactamente a las fuerzas aplicadas a un objeto paralelo a una superficie hasta el límite especificado por el coeficiente de fricción estática ( ) multiplicado por la fuerza normal ( ). En otras palabras, la magnitud de la fuerza de fricción estática satisface la desigualdad:
La fuerza de fricción cinética ( ) es típicamente independiente tanto de las fuerzas aplicadas como del movimiento del objeto. Por lo tanto, la magnitud de la fuerza es igual a:
donde es el coeficiente de fricción cinética . El coeficiente de fricción cinética normalmente es menor que el coeficiente de fricción estática. [17] : 267–271
Tensión
Las fuerzas de tensión se pueden modelar utilizando cuerdas ideales que no tienen masa, no tienen fricción, son irrompibles y no se estiran. Se pueden combinar con poleas ideales , que permiten que las cuerdas ideales cambien de dirección física. Las cuerdas ideales transmiten fuerzas de tensión instantáneamente en pares de acción-reacción de modo que si dos objetos están conectados por una cuerda ideal, cualquier fuerza dirigida a lo largo de la cuerda por el primer objeto está acompañada por una fuerza dirigida a lo largo de la cuerda en la dirección opuesta por el segundo objeto. [43] Al conectar la misma cuerda varias veces al mismo objeto mediante el uso de una configuración que utiliza poleas móviles, la fuerza de tensión sobre una carga se puede multiplicar. Por cada cuerda que actúa sobre una carga, otro factor de la fuerza de tensión en la cuerda actúa sobre la carga. Tales máquinas permiten una ventaja mecánica para un aumento correspondiente en la longitud de la cuerda desplazada necesaria para mover la carga. Estos efectos en tándem resultan en última instancia en la conservación de la energía mecánica ya que el trabajo realizado sobre la carga es el mismo sin importar cuán complicada sea la máquina. [4] : cap.12 [5] [44]
Primavera

Una fuerza elástica simple actúa para devolver un resorte a su longitud natural. Se considera que un resorte ideal no tiene masa, no tiene fricción, es irrompible y se puede estirar infinitamente. Dichos resortes ejercen fuerzas que empujan cuando se contraen o tiran cuando se extienden, en proporción al desplazamiento del resorte desde su posición de equilibrio. [45] Esta relación lineal fue descrita por Robert Hooke en 1676, por quien se nombró la ley de Hooke . Si es el desplazamiento, la fuerza ejercida por un resorte ideal es igual a: F = − k Δ x , {\displaystyle \mathbf {F} =-k\Delta \mathbf {x} ,} donde es la constante del resorte (o constante de fuerza), que es particular del resorte. El signo menos representa la tendencia de la fuerza a actuar en oposición a la carga aplicada. [4] : cap.12 [5]
Centrípeto
Para un objeto en movimiento circular uniforme , la fuerza neta que actúa sobre el objeto es igual a: [46] F = − m v 2 r r ^ , {\displaystyle \mathbf {F} =-{\frac {mv^{2}}{r}}{\hat {\mathbf {r} }},} donde es la masa del objeto, es la velocidad del objeto y es la distancia al centro de la trayectoria circular y es el vector unitario que apunta en dirección radial hacia afuera desde el centro. Esto significa que la fuerza neta sentida por el objeto siempre está dirigida hacia el centro de la trayectoria curva. Tales fuerzas actúan perpendicularmente al vector de velocidad asociado con el movimiento de un objeto y, por lo tanto, no cambian la rapidez del objeto (magnitud de la velocidad), sino solo la dirección del vector de velocidad. De manera más general, la fuerza neta que acelera un objeto se puede descomponer en un componente que es perpendicular a la trayectoria y uno que es tangencial a la trayectoria. Esto produce tanto la fuerza tangencial, que acelera el objeto ya sea ralentizándolo o acelerándolo, como la fuerza radial (centrípeta), que cambia su dirección. [4] : cap.12 [5]
Mecánica de medios continuos

Las leyes de Newton y la mecánica newtoniana en general se desarrollaron por primera vez para describir cómo las fuerzas afectan a partículas puntuales idealizadas en lugar de objetos tridimensionales. En la vida real, la materia tiene una estructura extendida y las fuerzas que actúan sobre una parte de un objeto pueden afectar a otras partes de un objeto. Para situaciones en las que la red que mantiene unidos a los átomos de un objeto puede fluir, contraerse, expandirse o cambiar de forma de alguna otra manera, las teorías de la mecánica de medios continuos describen la forma en que las fuerzas afectan al material. Por ejemplo, en fluidos extendidos , las diferencias de presión dan como resultado fuerzas que se dirigen a lo largo de los gradientes de presión de la siguiente manera:
donde es el volumen del objeto en el fluido y es la función escalar que describe la presión en todas las ubicaciones en el espacio. Los gradientes y diferenciales de presión dan como resultado la fuerza de flotación para fluidos suspendidos en campos gravitacionales, vientos en la ciencia atmosférica y la sustentación asociada con la aerodinámica y el vuelo . [4] : cap.12 [5]
Un ejemplo específico de una fuerza de este tipo que está asociada con la presión dinámica es la resistencia de fluidos: una fuerza corporal que resiste el movimiento de un objeto a través de un fluido debido a la viscosidad . Para el llamado " arrastre de Stokes ", la fuerza es aproximadamente proporcional a la velocidad, pero de dirección opuesta: F d = − b v , {\displaystyle \mathbf {F} _{\mathrm {d} }=-b\mathbf {v} ,} donde:
- es una constante que depende de las propiedades del fluido y de las dimensiones del objeto (normalmente el área de la sección transversal ), y
- es la velocidad del objeto. [4] : cap.12 [5]
Más formalmente, las fuerzas en la mecánica de medios continuos se describen completamente mediante un tensor de tensión con términos que se definen aproximadamente como σ = F A , {\displaystyle \sigma ={\frac {F}{A}},} donde es el área de la sección transversal relevante para el volumen para el que se está calculando el tensor de tensión. Este formalismo incluye términos de presión asociados con fuerzas que actúan normales al área de la sección transversal (las diagonales matriciales del tensor) así como términos de corte asociados con fuerzas que actúan paralelas al área de la sección transversal (los elementos fuera de la diagonal). El tensor de tensión tiene en cuenta las fuerzas que causan todas las deformaciones (deformaciones) incluyendo también las tensiones de tracción y las compresiones . [3] [5] : 133–134 [38] : 38-1–38-11
Ficticio
Existen fuerzas que dependen del marco de referencia , es decir, que aparecen debido a la adopción de marcos de referencia no newtonianos (es decir, no inerciales ) . Entre estas fuerzas se encuentran la fuerza centrífuga y la fuerza de Coriolis . [47] Estas fuerzas se consideran ficticias porque no existen en marcos de referencia que no estén acelerando. [4] : cap.12 [5] Debido a que estas fuerzas no son genuinas, también se las denomina "pseudofuerzas". [4] : 12-11
En la relatividad general , la gravedad se convierte en una fuerza ficticia que surge en situaciones en las que el espacio-tiempo se desvía de una geometría plana. [48]
Conceptos derivados de la fuerza
Rotación y par

Las fuerzas que hacen que los objetos extendidos giren están asociadas con pares de torsión . Matemáticamente, el par de torsión de una fuerza se define en relación con un punto de referencia arbitrario como el producto vectorial : τ = r × F , {\displaystyle {\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} ,} donde es el vector de posición del punto de aplicación de la fuerza en relación con el punto de referencia. [17] : 497
El par es el equivalente rotacional de la fuerza, de la misma manera que el ángulo es el equivalente rotacional de la posición , la velocidad angular de la velocidad y el momento angular del momento . Como consecuencia de la primera ley del movimiento de Newton, existe una inercia rotacional que garantiza que todos los cuerpos mantengan su momento angular a menos que actúe sobre ellos un par desequilibrado. Asimismo, la segunda ley del movimiento de Newton se puede utilizar para derivar una ecuación análoga para la aceleración angular instantánea del cuerpo rígido: donde
- es el momento de inercia del cuerpo
- es la aceleración angular del cuerpo. [17] : 502
Esto proporciona una definición del momento de inercia, que es el equivalente rotacional de la masa. En tratamientos más avanzados de la mecánica, donde se describe la rotación a lo largo de un intervalo de tiempo, el momento de inercia debe sustituirse por el tensor que, cuando se analiza adecuadamente, determina completamente las características de las rotaciones, incluidas la precesión y la nutación . [26] : 96–113
De manera equivalente, la forma diferencial de la Segunda Ley de Newton proporciona una definición alternativa del torque: [49] donde es el momento angular de la partícula.
La tercera ley del movimiento de Newton requiere que todos los objetos que ejercen torques experimenten torques iguales y opuestos, [50] y por lo tanto también implica directamente la conservación del momento angular para sistemas cerrados que experimentan rotaciones y revoluciones a través de la acción de torques internos.
Tirón
El tirón se define como la tasa de cambio de fuerza [51] : 131
El término se utiliza en análisis biomecánico, [52] evaluación atlética [53] y control robótico. [54] El segundo ("tirón"), el tercero ("arranque"), el cuarto ("sacudida") y las derivadas superiores rara vez se utilizan. [51]
Integrales cinemáticas
Las fuerzas se pueden utilizar para definir una serie de conceptos físicos mediante la integración con respecto a las variables cinemáticas . Por ejemplo, la integración con respecto al tiempo da la definición de impulso : [55] que, según la segunda ley de Newton, debe ser equivalente al cambio en el momento (lo que da lugar al teorema del momento del impulso ).
De manera similar, la integración con respecto a la posición da una definición para el trabajo realizado por una fuerza: [4] : 13-3 W = ∫ x 1 x 2 F ⋅ d x , {\displaystyle W=\int _{\mathbf {x} _{1}}^{\mathbf {x} _{2}}{\mathbf {F} \cdot {\mathrm {d} \mathbf {x} }},} que es equivalente a cambios en la energía cinética (lo que produce el teorema de trabajo-energía ). [4] : 13-3
La potencia P es la tasa de cambio d W /d t del trabajo W , a medida que la trayectoria se extiende por un cambio de posición en un intervalo de tiempo d t : [4] : 13-2 por lo que con v = d x / d t {\displaystyle \mathbf {v} =\mathrm {d} \mathbf {x} /\mathrm {d} t} la velocidad .
Energía potencial
En lugar de una fuerza, a menudo se utiliza el concepto matemáticamente relacionado de un campo de energía potencial . Por ejemplo, la fuerza gravitacional que actúa sobre un objeto puede verse como la acción del campo gravitacional que está presente en la ubicación del objeto. Reformulando matemáticamente la definición de energía (a través de la definición de trabajo ), un campo escalar potencial se define como aquel campo cuyo gradiente es igual y opuesto a la fuerza producida en cada punto:
Las fuerzas se pueden clasificar como conservativas o no conservativas. Las fuerzas conservativas son equivalentes al gradiente de un potencial, mientras que las fuerzas no conservativas no lo son. [4] : cap.12 [5]
Conservación
Una fuerza conservativa que actúa sobre un sistema cerrado tiene un trabajo mecánico asociado que permite que la energía se convierta únicamente entre formas cinéticas o potenciales . Esto significa que, para un sistema cerrado, la energía mecánica neta se conserva siempre que una fuerza conservativa actúe sobre el sistema. La fuerza, por lo tanto, está relacionada directamente con la diferencia de energía potencial entre dos ubicaciones diferentes en el espacio, [56] y puede considerarse un artefacto del campo potencial de la misma manera que la dirección y la cantidad de un flujo de agua pueden considerarse un artefacto del mapa de contorno de la elevación de un área. [4] : cap.12 [5]
Las fuerzas conservativas incluyen la gravedad , la fuerza electromagnética y la fuerza de resorte . Cada una de estas fuerzas tiene modelos que dependen de una posición que a menudo se da como un vector radial que emana de potenciales simétricos esféricos . [57] A continuación se ofrecen algunos ejemplos de esto:
Para la gravedad: donde es la constante gravitacional , y es la masa del objeto n .
Para fuerzas electrostáticas: donde es la permitividad eléctrica del espacio libre , y es la carga eléctrica del objeto n .
Para fuerzas de resorte: donde es la constante del resorte . [4] : cap.12 [5]
En ciertos escenarios físicos, es imposible modelar fuerzas como debidas a un simple gradiente de potenciales. Esto se debe a menudo a un promedio estadístico macroscópico de microestados . Por ejemplo, la fricción estática es causada por los gradientes de numerosos potenciales electrostáticos entre los átomos , pero se manifiesta como un modelo de fuerza que es independiente de cualquier vector de posición a macroescala. Las fuerzas no conservativas distintas de la fricción incluyen otras fuerzas de contacto , tensión , compresión y arrastre . Para cualquier descripción suficientemente detallada, todas estas fuerzas son el resultado de las conservadoras, ya que cada una de estas fuerzas macroscópicas son los resultados netos de los gradientes de potenciales microscópicos. [4] : cap.12 [5]
La conexión entre las fuerzas no conservativas macroscópicas y las fuerzas conservativas microscópicas se describe mediante un tratamiento detallado con mecánica estadística . En sistemas cerrados macroscópicos, las fuerzas no conservativas actúan para cambiar las energías internas del sistema y a menudo están asociadas con la transferencia de calor. Según la segunda ley de la termodinámica , las fuerzas no conservativas necesariamente resultan en transformaciones de energía dentro de sistemas cerrados desde condiciones ordenadas a más aleatorias a medida que aumenta la entropía . [4] : cap.12 [5]
Unidades
La unidad de fuerza del SI es el newton (símbolo N), que es la fuerza necesaria para acelerar una masa de un kilogramo a una velocidad de un metro por segundo al cuadrado, o kg·m·s −2 . La unidad CGS correspondiente es la dina , la fuerza necesaria para acelerar una masa de un gramo en un centímetro por segundo al cuadrado, o g·cm·s −2 . Un newton es, por tanto, igual a 100.000 dinas. [58]
La unidad de fuerza gravitacional inglesa pie-libra-segundo es la libra-fuerza (lbf), definida como la fuerza ejercida por la gravedad sobre una masa de libra en el campo gravitacional estándar de 9,80665 m·s −2 . [58] La libra-fuerza proporciona una unidad de masa alternativa: un slug es la masa que se acelerará en un pie por segundo al cuadrado cuando actúe sobre ella una libra-fuerza. [58] Una unidad de fuerza alternativa en un sistema pie-libra-segundo diferente, el sistema fps absoluto, es el poundal , definido como la fuerza requerida para acelerar una masa de una libra a una velocidad de un pie por segundo al cuadrado. [58]
La libra-fuerza tiene una contraparte métrica, menos comúnmente utilizada que el newton: el kilogramo-fuerza (kgf) (a veces kilopondio), es la fuerza ejercida por la gravedad estándar sobre un kilogramo de masa. El kilogramo-fuerza conduce a una unidad de masa alternativa, pero raramente utilizada: el slug métrico (a veces mug o hyl) es aquella masa que acelera a 1 m·s −2 cuando se somete a una fuerza de 1 kgf. El kilogramo-fuerza no es parte del sistema SI moderno y generalmente está en desuso; a veces se usa para expresar el peso de la aeronave, el empuje de los aviones, la tensión de los radios de las bicicletas, los ajustes de la llave dinamométrica y el par de salida del motor. [58]
| Newton | dina | kilogramo-fuerza , kilopondio | libra-fuerza | Poundal | |
|---|---|---|---|---|---|
| 1 N | ≡ 1 kg⋅m2/ s2 | = 10 5 dinares | ≈ 0,101 97 kp | ≈ 0,224 81 libras F | ≈ 7.2330 libras esterlinas |
| 1 dina | = 10 −5 N | ≡ 1 g⋅cm/ s2 | ≈ 1,0197 × 10 −6 kp | ≈ 2,2481 × 10 −6 lbF | ≈ 7,2330 × 10 −5 pdl |
| 1 kilómetro | = 9.806 65 N | = 980 665 dinares | ≡ g n × 1 kg | ≈ 2,2046 libras F | ≈ 70.932 libras esterlinas |
| 1 libra F | ≈ 4.448 222 N | ≈ 444 822 dinares | ≈ 0,453 59 kilómetros | ≡ g n × 1 libra | ≈ 32.174 libras esterlinas |
| 1 paquete | ≈ 0,138 255 N | ≈ 13 825 dinares | ≈ 0,014 098 kp | ≈ 0,031 081 libras F | ≡ 1 libra⋅ pie /s 2 |
| El valor de g n (9.806 65 m/s 2 ), tal como se utiliza en la definición oficial del kilogramo-fuerza, se utiliza aquí para todas las unidades gravitacionales. | |||||
- Véase también Tonelada-fuerza .
Revisiones del concepto de fuerza
A principios del siglo XX surgieron nuevas ideas físicas para explicar los resultados experimentales en los ámbitos astronómico y submicroscópico. Como se analiza más adelante, la relatividad altera la definición de momento y la mecánica cuántica reutiliza el concepto de "fuerza" en contextos microscópicos en los que las leyes de Newton no se aplican directamente.
Teoría especial de la relatividad
En la teoría especial de la relatividad , la masa y la energía son equivalentes (como se puede ver al calcular el trabajo requerido para acelerar un objeto). Cuando la velocidad de un objeto aumenta, también lo hace su energía y, por lo tanto, su masa equivalente (inercia). Por lo tanto, se requiere más fuerza para acelerarlo la misma cantidad de lo que lo hizo a una velocidad menor. La segunda ley de Newton, sigue siendo válida porque es una definición matemática. [36] : 855–876 Pero para que el momento se conserve a la velocidad relativa relativista, , el momento debe redefinirse como: donde es la masa en reposo y la velocidad de la luz .
La expresión que relaciona fuerza y aceleración para una partícula con masa en reposo constante distinta de cero que se mueve en la dirección a velocidad es: [59] : 216 donde γ = 1 1 − v 2 / c 2 . {\displaystyle \gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}.} se llama factor de Lorentz . El factor de Lorentz aumenta abruptamente a medida que la velocidad relativa se acerca a la velocidad de la luz. En consecuencia, se debe aplicar una fuerza cada vez mayor para producir la misma aceleración a una velocidad extrema. La velocidad relativa no puede alcanzar . [59] : 26 [4] : §15–8 Si es muy pequeño en comparación con , entonces es muy cercano a 1 y es una aproximación cercana. Incluso para su uso en relatividad, se puede restaurar la forma de mediante el uso de cuatro vectores . Esta relación es correcta en relatividad cuando es la cuádruple fuerza , es la masa invariante y es la cuádruple aceleración . [60]
La teoría general de la relatividad incorpora un cambio más radical respecto de la forma newtoniana de pensar sobre la fuerza, en particular la fuerza gravitacional. Esta nueva concepción de la naturaleza de la gravedad se describe con más detalle a continuación.
Mecánica cuántica
La mecánica cuántica es una teoría de la física desarrollada originalmente para comprender los fenómenos microscópicos: el comportamiento a escala de moléculas, átomos o partículas subatómicas. En términos generales y vagos, cuanto más pequeño es un sistema, más requerirá un modelo matemático adecuado para comprender los efectos cuánticos. La base conceptual de la física cuántica es diferente a la de la física clásica. En lugar de pensar en cantidades como la posición, el momento y la energía como propiedades que tiene un objeto , se considera qué resultado podría aparecer cuando se realiza una medición de un tipo elegido. La mecánica cuántica permite al físico calcular la probabilidad de que una medición elegida produzca un resultado particular. [61] [62] El valor esperado para una medición es el promedio de los posibles resultados que podría producir, ponderados por sus probabilidades de ocurrencia. [63]
En mecánica cuántica, las interacciones se describen típicamente en términos de energía en lugar de fuerza. El teorema de Ehrenfest proporciona una conexión entre los valores esperados cuánticos y el concepto clásico de fuerza, una conexión que es necesariamente inexacta, ya que la física cuántica es fundamentalmente diferente de la clásica. En física cuántica, la regla de Born se utiliza para calcular los valores esperados de una medición de posición o una medición de momento. Estos valores esperados generalmente cambiarán con el tiempo; es decir, dependiendo del momento en el que (por ejemplo) se realice una medición de posición, variarán las probabilidades de sus diferentes resultados posibles. El teorema de Ehrenfest dice, en términos generales, que las ecuaciones que describen cómo estos valores esperados cambian con el tiempo tienen una forma que recuerda a la segunda ley de Newton, con una fuerza definida como la derivada negativa de la energía potencial. Sin embargo, cuanto más pronunciados sean los efectos cuánticos en una situación dada, más difícil será derivar conclusiones significativas de esta semejanza. [64] [65]
La mecánica cuántica también introduce dos nuevas restricciones que interactúan con fuerzas a escala submicroscópica y que son especialmente importantes para los átomos. A pesar de la fuerte atracción del núcleo, el principio de incertidumbre limita la extensión mínima de una distribución de probabilidad de electrones [66] y el principio de exclusión de Pauli impide que los electrones compartan la misma distribución de probabilidad. [67] Esto da lugar a una presión emergente conocida como presión de degeneración . El equilibrio dinámico entre la presión de degeneración y la fuerza electromagnética atractiva proporciona estabilidad a los átomos, moléculas, líquidos y sólidos . [68]
Teoría cuántica de campos

En la física de partículas moderna , las fuerzas y la aceleración de las partículas se explican como un subproducto matemático del intercambio de bosones gauge portadores de momento . Con el desarrollo de la teoría cuántica de campos y la relatividad general , se comprendió que la fuerza es un concepto redundante que surge de la conservación del momento ( momento cuántico en relatividad y momento de partículas virtuales en electrodinámica cuántica ). La conservación del momento se puede derivar directamente de la homogeneidad o simetría del espacio y, por lo tanto, se considera generalmente más fundamental que el concepto de fuerza. Por lo tanto, las fuerzas fundamentales actualmente conocidas se consideran con mayor precisión como " interacciones fundamentales ". [6] : 199–128
Aunque se necesitan descripciones matemáticas sofisticadas para predecir, con todo detalle, el resultado de tales interacciones, existe una forma conceptualmente sencilla de describirlas mediante el uso de diagramas de Feynman . En un diagrama de Feynman, cada partícula de materia se representa como una línea recta (véase línea del mundo ) que viaja a través del tiempo, que normalmente aumenta hacia arriba o hacia la derecha en el diagrama. Las partículas de materia y antimateria son idénticas excepto por su dirección de propagación a través del diagrama de Feynman. Las líneas del mundo de las partículas se intersecan en los vértices de interacción , y el diagrama de Feynman representa cualquier fuerza que surja de una interacción como si ocurriera en el vértice con un cambio instantáneo asociado en la dirección de las líneas del mundo de las partículas. Los bosones de calibre se emiten lejos del vértice como líneas onduladas y, en el caso del intercambio de partículas virtuales, se absorben en un vértice adyacente. [69] La utilidad de los diagramas de Feynman es que otros tipos de fenómenos físicos que forman parte del cuadro general de interacciones fundamentales pero que están conceptualmente separados de las fuerzas también se pueden describir utilizando las mismas reglas. Por ejemplo, un diagrama de Feynman puede describir con sucinto detalle cómo un neutrón se desintegra en un electrón , un protón y un antineutrino , una interacción mediada por el mismo bosón de calibre que es responsable de la fuerza nuclear débil . [69]
Interacciones fundamentales
Todas las fuerzas conocidas del universo se clasifican en cuatro interacciones fundamentales . Las fuerzas fuerte y débil actúan sólo a distancias muy cortas, y son responsables de las interacciones entre partículas subatómicas , incluyendo nucleones y núcleos compuestos . La fuerza electromagnética actúa entre cargas eléctricas , y la fuerza gravitacional actúa entre masas . Todas las demás fuerzas de la naturaleza se derivan de estas cuatro interacciones fundamentales que operan dentro de la mecánica cuántica , incluyendo las restricciones introducidas por la ecuación de Schrödinger y el principio de exclusión de Pauli . [67] Por ejemplo, la fricción es una manifestación de la fuerza electromagnética que actúa entre átomos de dos superficies. Las fuerzas en resortes , modeladas por la ley de Hooke , también son el resultado de fuerzas electromagnéticas. Las fuerzas centrífugas son fuerzas de aceleración que surgen simplemente de la aceleración de marcos de referencia giratorios . [4] : 12-11 [5] : 359
Las teorías fundamentales de las fuerzas se desarrollaron a partir de la unificación de diferentes ideas. Por ejemplo, la teoría universal de la gravitación de Newton mostró que la fuerza responsable de la caída de los objetos cerca de la superficie de la Tierra es también la fuerza responsable de la caída de los cuerpos celestes sobre la Tierra (la Luna ) y alrededor del Sol (los planetas). Michael Faraday y James Clerk Maxwell demostraron que las fuerzas eléctricas y magnéticas estaban unificadas mediante una teoría del electromagnetismo. En el siglo XX, el desarrollo de la mecánica cuántica condujo a una comprensión moderna de que las tres primeras fuerzas fundamentales (todas excepto la gravedad) son manifestaciones de la materia ( fermiones ) que interactúan mediante el intercambio de partículas virtuales llamadas bosones de gauge . [70] Este modelo estándar de la física de partículas asume una similitud entre las fuerzas y llevó a los científicos a predecir la unificación de las fuerzas débil y electromagnética en la teoría electrodébil , que posteriormente fue confirmada por la observación. [71]
| Propiedad/Interacción | Gravitación | Débil | Electromagnético | Fuerte | |
|---|---|---|---|---|---|
| (Electrodébil) | Fundamental | Residual | |||
| Actúa sobre: | Masa - Energía | Sabor | Carga eléctrica | Carga de color | Núcleos atómicos |
| Partículas que experimentan: | Todo | Quarks, leptones | Cargado eléctricamente | Quarks, gluones | Hadrones |
| Partículas mediadoras: | Gravitón (aún no observado) | W + W − Z 0 | gamma | Gluones | Mesones |
| Fuerza en la escala de quarks: | 10 −41 | 10 −4 | 1 | 60 | No aplicable a los quarks |
| Fuerza en la escala de protones/neutrones: | 10 −36 | 10 −7 | 1 | No aplicable a los hadrones | 20 |
Gravitacional

La ley de gravitación de Newton es un ejemplo de acción a distancia : un cuerpo, como el Sol, ejerce una influencia sobre cualquier otro cuerpo, como la Tierra, sin importar cuán lejos estén. Además, esta acción a distancia es instantánea. Según la teoría de Newton, el cambio de posición de un cuerpo cambia las atracciones gravitacionales que sienten todos los demás cuerpos, todos en el mismo instante de tiempo. Albert Einstein reconoció que esto era inconsistente con la relatividad especial y su predicción de que las influencias no pueden viajar más rápido que la velocidad de la luz . Entonces, buscó una nueva teoría de la gravitación que fuera relativistamente consistente. [74] [75] La órbita de Mercurio no coincidía con la predicha por la ley de gravitación de Newton. Algunos astrofísicos predijeron la existencia de un planeta no descubierto ( Vulcano ) que podría explicar las discrepancias. Cuando Einstein formuló su teoría de la relatividad general (RG) se centró en la problemática órbita de Mercurio y descubrió que su teoría agregó una corrección, que podría explicar la discrepancia . Esta fue la primera vez que se demostró que la teoría de la gravedad de Newton era inexacta. [76]
Desde entonces, la relatividad general ha sido reconocida como la teoría que mejor explica la gravedad. En la relatividad general, la gravitación no se considera una fuerza, sino que los objetos que se mueven libremente en campos gravitatorios viajan bajo su propia inercia en líneas rectas a través del espacio-tiempo curvo , definido como el camino espacio-temporal más corto entre dos eventos espacio-temporales. Desde la perspectiva del objeto, todo movimiento ocurre como si no hubiera gravitación alguna. Es solo cuando se observa el movimiento en un sentido global que se puede observar la curvatura del espacio-tiempo y se infiere la fuerza a partir de la trayectoria curva del objeto. Por lo tanto, la trayectoria en línea recta en el espacio-tiempo se ve como una línea curva en el espacio, y se llama trayectoria balística del objeto. Por ejemplo, una pelota de baloncesto lanzada desde el suelo se mueve en una parábola , ya que está en un campo gravitatorio uniforme. Su trayectoria espacio-temporal es casi una línea recta, ligeramente curvada (con un radio de curvatura del orden de unos pocos años luz ). La derivada temporal del momento cambiante del objeto es lo que etiquetamos como "fuerza gravitacional". [5]
Electromagnético
Las ecuaciones de Maxwell y el conjunto de técnicas construidas en torno a ellas describen adecuadamente una amplia gama de la física que involucra la fuerza en la electricidad y el magnetismo. Esta teoría clásica ya incluye los efectos de la relatividad. [77] Para comprender las interacciones electromagnéticas cuantizadas entre partículas elementales se requiere la electrodinámica cuántica (o QED). En la QED, los fotones son partículas de intercambio fundamentales que describen todas las interacciones relacionadas con el electromagnetismo, incluida la fuerza electromagnética. [78]
Nuclear fuerte
Existen dos "fuerzas nucleares", que hoy en día se describen habitualmente como interacciones que tienen lugar en las teorías cuánticas de la física de partículas. La fuerza nuclear fuerte es la fuerza responsable de la integridad estructural de los núcleos atómicos y recibe su nombre de su capacidad para superar la repulsión electromagnética entre protones. [36] : 940 [79]
Hoy en día se entiende que la fuerza fuerte representa las interacciones entre quarks y gluones , tal como se detalla en la teoría de la cromodinámica cuántica (QCD). [80] La fuerza fuerte es la fuerza fundamental mediada por los gluones, que actúa sobre los quarks, los antiquarks y los propios gluones. La fuerza fuerte sólo actúa directamente sobre las partículas elementales. Se observa un residuo entre los hadrones (en particular, los nucleones en los núcleos atómicos), conocido como fuerza nuclear . Aquí la fuerza fuerte actúa indirectamente, transmitiéndose como gluones que forman parte de los mesones virtuales pi y rho , los transmisores clásicos de la fuerza nuclear. El fracaso de muchas búsquedas de quarks libres ha demostrado que las partículas elementales afectadas no son directamente observables. Este fenómeno se llama confinamiento de color . [81] : 232
Nuclear débil
Única entre las interacciones fundamentales, la fuerza nuclear débil no crea estados ligados. [82] La fuerza débil se debe al intercambio de los bosones pesados W y Z. Dado que la fuerza débil está mediada por dos tipos de bosones, se puede dividir en dos tipos de interacción o " vértices ": corriente cargada , que involucra a los bosones W + y W− eléctricamente cargados , y corriente neutra , que involucra a los bosones Z0 eléctricamente neutros . El efecto más conocido de la interacción débil es la desintegración beta (de neutrones en los núcleos atómicos) y la radiactividad asociada . [36] : 951 Este es un tipo de interacción de corriente cargada. La palabra "débil" deriva del hecho de que la intensidad del campo es unas 10 13 veces menor que la de la fuerza fuerte . Aún así, es más fuerte que la gravedad en distancias cortas. También se ha desarrollado una teoría electrodébil consistente, que muestra que las fuerzas electromagnéticas y la fuerza débil son indistinguibles a temperaturas superiores a aproximadamente10 15 K . [83] Tales temperaturas ocurrieron en las colisiones de plasma en los primeros momentos del Big Bang . [82] : 201
Véase también
- Fuerza de contacto : Fuerza entre dos objetos que están en contacto físico.
- Control de fuerza : el control de fuerza lo proporciona la máquina.
- Dinamómetro – Instrumento para medir fuerza
- Órdenes de magnitud (fuerza) : comparación de una amplia gama de fuerzas físicas
- Sistema de fuerzas paralelas – Situación en la ingeniería mecánica
- Cuerpo rígido : Objeto físico que no se deforma cuando se ejercen fuerzas o momentos sobre él.
- Fuerza específica – Concepto en física
Referencias
- ^ Cohen, Michael. «Mecánica clásica: una introducción crítica» (PDF) . Universidad de Pensilvania . Archivado (PDF) del original el 3 de julio de 2022. Consultado el 9 de enero de 2024 .
- ^ ab Heath, Thomas L. (1897). The Works of Archimedes [Las obras de Arquímedes]. Cambridge University Press . Consultado el 14 de octubre de 2007 a través de Internet Archive .
- ^ abcdefg Sears, Francis W .; Zemansky, Mark W .; Young, Hugh D. (1982). Física universitaria (6.ª ed.). Addison-Wesley. págs. 18–38. ISBN 0-201-07199-1.
- ^ abcdefghijklmnopqrstu vwxyz aa ab Feynman, Richard P. ; Leighton, Robert B. ; Sands, Matthew (2010). Las conferencias Feynman sobre física. Vol. I: Principalmente mecánica, radiación y calor (edición del nuevo milenio). Nueva York: Basic Books. ISBN 978-0465024933.
- ^ abcdefghijklmnopqrstu vwx Kleppner, Daniel; Kolenkow, Robert J. (2014). "Capítulo 3: Fuerzas y ecuaciones de movimiento". Introducción a la mecánica (2.ª ed.). Cambridge: Cambridge University Press. ISBN 978-0521198110.
- ^ ab Weinberg, S. (1994). Sueños de una teoría final . Libros antiguos. ISBN 978-0-679-74408-5.
- ^ Lang, Helen S. (1998). El orden de la naturaleza en la física de Aristóteles: el lugar y los elementos . Cambridge: Cambridge Univ. Press. ISBN 978-0521624534.
- ^ Hetherington, Norriss S. (1993). Cosmología: perspectivas históricas, literarias, filosóficas, religiosas y científicas. Biblioteca de referencia de humanidades Garland. pág. 100. ISBN 978-0-8153-1085-3.
- ^ Sorabji, Richard (2010). "Juan Filopono". Filopono y el rechazo de la ciencia aristotélica (2ª ed.). Instituto de Estudios Clásicos, Universidad de Londres. pag. 47.ISBN 978-1-905-67018-5. JSTOR 44216227. OCLC 878730683.
- ^ Maier, Anneliese (1982). Sargent, Steven D. (ed.). En el umbral de la ciencia exacta . University of Pennsylvania Press. pág. 79. ISBN 978-0-812-27831-6.OCLC 495305340 .
- ^ de Drake, Stillman (1978). Galileo en acción . Chicago: University of Chicago Press. ISBN 0-226-16226-5.
- ^ LoLordo, Antonia (2007). Pierre Gassendi y el nacimiento de la filosofía moderna temprana. Nueva York: Cambridge University Press. pp. 175–180. ISBN 978-0-511-34982-9.OCLC 182818133 .
- ^ Arnoldo, VI ; Kozlov, VV; Neĩshtadt, AI (1988). "Aspectos matemáticos de la mecánica clásica y celeste". Enciclopedia de Ciencias Matemáticas, Sistemas Dinámicos III. vol. 3. Anosov, DV Berlín: Springer-Verlag. ISBN 0-387-17002-2.OCLC 16404140 .
- ^ abcdef Newton, Isaac (1999). Los Principia: Principios matemáticos de la filosofía natural . Berkeley: University of California Press. ISBN 978-0-520-08817-7.Esta es una traducción reciente al inglés de I. Bernard Cohen y Anne Whitman, con la ayuda de Julia Budenz.
- ^ Howland, RA (2006). Dinámica intermedia: un enfoque algebraico lineal (edición en línea-ausg.). Nueva York: Springer. pp. 255–256. ISBN 978-0387280592.
- ^ Mermin, N. David (2005). Ya era hora: entender la relatividad de Einstein . Princeton University Press. ISBN 978-0-691-21877-9.
- ^ abcdefghi Ling, Samuel J.; Sanny, Jeff; Moebs, William; et al. (2021). Física universitaria, volumen 1. OpenStax . ISBN 978-1-947-17220-3.
- ^ Hellingman, C. (1992). "Newton's third law revisited". Phys. Educ . 27 (2): 112–115. Bibcode :1992PhyEd..27..112H. doi :10.1088/0031-9120/27/2/011. S2CID 250891975.
Citando a Newton en los
Principia
: No es una acción por la cual el Sol atrae a Júpiter, y otra por la cual Júpiter atrae al Sol; sino que es una acción por la cual el Sol y Júpiter se esfuerzan mutuamente por acercarse.
- ^ Resnick, Robert; Halliday, David; Krane, Kenneth S. (2002). Física. 1 (5.ª ed.). ISBN 978-0-471-32057-9Cualquier fuerza individual
es sólo un aspecto de una interacción mutua entre dos cuerpos.
- ^ Landau, LD ; Akhiezer, AI ; Lifshitz, AM (1967). Física general; mecánica y física molecular . Oxford: Pergamon Press. ISBN 978-0-08-003304-4.Traducido por: JB Sykes, AD Petford y CL Petford. LCCN 67--30260. En la sección 7, págs. 12-14, este libro define la fuerza como dp/dt .
- ^ Kibble, Tom WB; Berkshire, Frank H. (2004). Mecánica clásica (5.ª ed.). Londres: Imperial College Press. ISBN 1860944248.Según la página 12, "[La fuerza] puede, por supuesto, introducirse definiéndola a través de la segunda ley de Newton".
- ^ de Lange, OL; Pierrus, J. (2010). Problemas resueltos en mecánica clásica . Oxford: Oxford University Press. ISBN 978-0-19-958252-5.Según la página 3, "[la segunda ley del movimiento de Newton] puede considerarse como una fuerza definitoria".
- ^ José, Jorge V. ; Saletan, Eugene J. (1998). Dinámica clásica: un enfoque contemporáneo. Cambridge [Inglaterra]: Cambridge University Press. p. 9. ISBN 978-1-139-64890-5.OCLC 857769535 .
- ^ Frautschi, Steven C. ; Olenick, Richard P. ; Apostol, Tom M. ; Goodstein, David L. (2007). El universo mecánico: mecánica y calor (edición avanzada). Cambridge [Cambridgeshire]: Cambridge University Press. pág. 134. ISBN 978-0-521-71590-4.OCLC 227002144 .
- ^ ab Thornton, Stephen T.; Marion, Jerry B. (2004). Dinámica clásica de partículas y sistemas (5.ª ed.). Thomson Brooks/Cole. págs. 49-50. ISBN 0-534-40896-6.
- ^ ab Landau, Lev D .; Lifshitz, Evgeny M. (1969). Mecánica . Curso de física teórica . Vol. 1. Traducido por Sykes, JB; Bell, JS (2.ª ed.). Pergamon Press . ISBN 978-0-080-06466-6.
- ^ Jammer, Max (1999). Conceptos de fuerza: un estudio sobre los fundamentos de la dinámica (edición facsímil). Mineola, NY: Dover Publications. pp. 220–222. ISBN 978-0486406893.
- ^ Noll, Walter (abril de 2007). "Sobre el concepto de fuerza" (PDF) . Universidad Carnegie Mellon . Consultado el 28 de octubre de 2013 .
- ^ "Introducción a los diagramas de cuerpo libre". Menú del tutorial de física . Universidad de Guelph . Archivado desde el original el 16 de enero de 2008 . Consultado el 2 de enero de 2008 .
- ^ Henderson, Tom (2004). "El aula de física". El aula de física y Mathsoft Engineering & Education, Inc. Archivado desde el original el 2008-01-01 . Consultado el 2008-01-02 .
- ^ "Equilibrio estático". Física Equilibrio estático (fuerzas y pares) . Universidad de las Islas Vírgenes . Archivado desde el original el 19 de octubre de 2007. Consultado el 2 de enero de 2008 .
- ^ Cook, AH (1965). "Una nueva determinación absoluta de la aceleración debida a la gravedad en el Laboratorio Nacional de Física". Nature . 208 (5007): 279. Bibcode :1965Natur.208..279C. doi : 10.1038/208279a0 . S2CID 4242827.
- ^ ab Young, Hugh; Freedman, Roger; Sears, Francis; y Zemansky, Mark (1949) Física universitaria . Pearson Education. págs. 59–82.
- ^ Watkins, Thayer. "Análisis de perturbaciones, regulares y singulares". Departamento de Economía . Universidad Estatal de San José. Archivado desde el original el 10 de febrero de 2011. Consultado el 5 de enero de 2008 .
- ^ Kollerstrom, Nick (2001). "El descubrimiento de Neptuno. El caso británico en favor de la copredicción". University College London. Archivado desde el original el 11 de noviembre de 2005. Consultado el 19 de marzo de 2007 .
- ^ abcde Cutnell, John D.; Johnson, Kenneth W. (2004). Física (6.ª ed.). Hoboken, Nueva Jersey: Wiley. ISBN 978-0-471-44895-2.
- ^ Coulomb, Charles (1784). "Investigaciones teóricas y experimentales sobre la fuerza de torsión y la elasticidad de los hilos de metal". Historia de la Academia Real de Ciencias : 229–269.
- ^ ab Feynman, Richard P. ; Leighton, Robert B. ; Sands, Matthew (2010). Las conferencias Feynman sobre física. Vol. II: Principalmente electromagnetismo y materia (edición del nuevo milenio). Nueva York: Basic Books. ISBN 978-0465024940.
- ^ Tonnelat, Marie-Antoinette (1966). Los principios de la teoría electromagnética y de la relatividad. Dordrecht: D. Reidel. p. 85. ISBN 90-277-0107-5.OCLC 844001 .
- ^ Ling, Samuel J.; Sanny, Jeff; Moebs, William (2021). Física Universitaria, Volumen 2. OpenStax . ISBN 978-1-947-17221-0.
- ^ Scharf, Toralf (2007). "Capítulo 2". Luz polarizada en cristales líquidos y polímeros . John Wiley and Sons. pág. 19. ISBN 978-0-471-74064-3.
- ^ Duffin, William (1980). Electricidad y magnetismo (3.ª ed.). McGraw-Hill. pp. 364–383. ISBN 978-0-07-084111-6.
- ^ "Fuerza de tensión". Física no basada en cálculo I. Archivado desde el original el 27 de diciembre de 2007. Consultado el 4 de enero de 2008 .
- ^ Fitzpatrick, Richard (2 de febrero de 2006). "Cuerdas, poleas e inclinaciones" . Consultado el 4 de enero de 2008 .
- ^ Nave, Carl Rod. "Elasticidad". HyperPhysics . Universidad de Guelph . Consultado el 28 de octubre de 2013 .
- ^ Nave, Carl Rod. "Fuerza centrípeta". HyperPhysics . Universidad de Guelph . Consultado el 28 de octubre de 2013 .
- ^ Mallette, Vincent (1982–2008). "La fuerza de Coriolis". Publicaciones en Ciencias y Matemáticas, Informática y Humanidades . Inwit Publishing, Inc. Consultado el 4 de enero de 2008 .
- ^ Choquet-Bruhat, Yvonne (2009). Relatividad general y ecuaciones de Einstein. Oxford: Oxford University Press. pág. 39. ISBN 978-0-19-155226-7.OCLC 317496332 .
- ^ Nave, Carl Rod. "Segunda ley de Newton: rotación". HyperPhysics . Universidad de Guelph . Consultado el 28 de octubre de 2013 .
- ^ Fitzpatrick, Richard (7 de enero de 2007). «La tercera ley del movimiento de Newton» . Consultado el 4 de enero de 2008 .
- ^ ab Jazar, Reza N. (2011). Dinámica avanzada: cuerpos rígidos, multicuerpos y aplicaciones aeroespaciales . Hoboken, NJ: Wiley. ISBN 978-0-470-39835-7.
- ^ Lin, David C.; McGowan, Craig P.; Blum, Kyle P.; Ting, Lena H. (12 de septiembre de 2019). "Yank: la derivada temporal de la fuerza es una variable biomecánica importante en los sistemas sensoriomotores". Revista de biología experimental . 222 (18): jeb180414. doi :10.1242/jeb.180414. ISSN 0022-0949. PMC 6765171 . PMID 31515280.
- ^ Harry, John R.; Barker, Leland A.; Tinsley, Grant M.; Krzyszkowski, John; Chowning, Luke D.; McMahon, John J.; Lake, Jason (5 de mayo de 2021). "Relaciones entre las métricas de rendimiento del salto vertical con contramovimiento, las variables de estrategia y la asimetría entre extremidades en mujeres". Sports Biomechanics : 1–19. doi :10.1080/14763141.2021.1908412. ISSN 1476-3141. PMID 33947320.
- ^ Rosendo, Andre; Tanaka, Takayuki; Kaneko, Shun'ichi (20 de abril de 2012). "Un método de coeficiente variable basado en Yank para un sistema de asistencia de potencia semiactiva de baja potencia". Revista de robótica y mecatrónica . 24 (2): 291–297. doi : 10.20965/jrm.2012.p0291 .
- ^ Hibbeler, Russell C. (2010). Ingeniería mecánica (12.ª ed.). Pearson Prentice Hall. pág. 222. ISBN 978-0-13-607791-6.
- ^ Singh, Sunil Kumar (25 de agosto de 2007). "Fuerza conservadora". Connexions . Consultado el 4 de enero de 2008 .
- ^ Davis, Doug. "Conservación de la energía". Física general . Consultado el 4 de enero de 2008 .
- ^ abcde Wandmacher, Cornelius; Johnson, Arnold (1995). Unidades métricas en ingeniería. Publicaciones de la ASCE. pág. 15. ISBN 978-0-7844-0070-8.
- ^ ab French, AP (1972). Relatividad especial . Serie de introducción a la física del MIT (edición reimpresa). Londres: Chapman & Hall. ISBN 978-0-17-771075-9.
- ^ Wilson, John B. "Cuatro vectores (4-Vectors) de la relatividad especial: un estudio de la física elegante". El reino de la ciencia: el universo virtual de ciencia y tecnología de John . Archivado desde el original el 26 de junio de 2009. Consultado el 4 de enero de 2008 .
- ^ Mermin, N. David (1993). "Variables ocultas y los dos teoremas de John Bell". Reseñas de Física Moderna . 65 (3): 803–815. arXiv : 1802.10119 . Bibcode :1993RvMP...65..803M. doi :10.1103/RevModPhys.65.803. S2CID 119546199.
Una doctrina cuántica fundamental sostiene que una medición no revela, en general, un valor preexistente de la propiedad medida.
- ^ Schaffer, Kathryn; Barreto Lemos, Gabriela (24 de mayo de 2019). "Eliminación de la cosificación: una introducción al "qué" y al "entonces qué" de la física cuántica". Fundamentos de la ciencia . 26 : 7–26. arXiv : 1908.07936 . doi :10.1007/s10699-019-09608-5. ISSN 1233-1821. S2CID 182656563.
- ^ Marshman, Emily; Singh, Chandralekha (1 de marzo de 2017). "Investigación y mejora de la comprensión de los estudiantes sobre las distribuciones de probabilidad para medir observables físicos en mecánica cuántica". Revista Europea de Física . 38 (2): 025705. Bibcode :2017EJPh...38b5705M. doi : 10.1088/1361-6404/aa57d1 . ISSN 0143-0807. S2CID 126311599.
- ^ Cohen-Tannoudji, Claude ; Diu, Bernardo; Laloë, Franck (2005). Mecánica Cuántica . Traducido por Hemley, Susan Reid; Ostrowsky, Nicole; Ostrowsky, Dan. John Wiley e hijos. pag. 242.ISBN 0-471-16433-X.
- ^ Peres, Asher (1993). Teoría cuántica: conceptos y métodos . Kluwer . Pág. 302. ISBN. 0-7923-2549-4.OCLC 28854083 .
- ^ Lieb, Elliott H. (1976-10-01). "La estabilidad de la materia". Reseñas de Física Moderna . 48 (4): 553–569. Bibcode :1976RvMP...48..553L. doi :10.1103/RevModPhys.48.553. ISSN 0034-6861.
el hecho de que si uno intenta comprimir una función de onda
en cualquier lugar
, la energía cinética aumentará. Este principio fue propuesto por Sobolev (1938)...
- ^ ab Lieb, Elliott H. (1990). "La estabilidad de la materia: de los átomos a las estrellas". Boletín de la Sociedad Matemática Americana . 22 (1): 1–49. doi : 10.1090/S0273-0979-1990-15831-8 . ISSN 0273-0979.
La materia en masa es estable y tiene un volumen proporcional al número de partículas, debido al principio de exclusión de Pauli para los fermiones (es decir, los electrones). Efectivamente, los electrones se comportan como un fluido con densidad de energía
, y esto limita la compresión causada por las fuerzas electrostáticas atractivas.
- ^ Griffiths (2005). Introducción a la mecánica cuántica, segunda edición . Londres, Reino Unido: Prentice Hall . pp. 221–223. ISBN. 0131244051.
- ^ ab Shifman, Mikhail (1999). Conferencias ITEP sobre física de partículas y teoría de campos . World Scientific. ISBN 978-981-02-2639-8.
- ^ "Fermiones y bosones". The Particle Adventure . Archivado desde el original el 18 de diciembre de 2007. Consultado el 4 de enero de 2008 .
- ^ Jarlskog, Cecilia (12 de octubre de 1999). «Material adicional sobre el Premio Nobel de Física de 1999». Premio Nobel . Consultado el 26 de julio de 2023 .
- ^ "Modelo estándar de partículas e interacciones". Proyecto de Educación en Física Contemporánea. 2000. Archivado desde el original el 2 de enero de 2017. Consultado el 2 de enero de 2017 .
- ^ "Una nueva y poderosa sonda para agujeros negros llega a Paranal" . Consultado el 13 de agosto de 2015 .
- ^ Misner, Charles W .; Thorne, Kip S .; Wheeler, John Archibald (1973). Gravitación . San Francisco: WH Freeman . Págs. 3-5. ISBN. 978-0-7167-0344-0.
- ^ Choquet-Bruhat, Yvonne (2009). Relatividad general y ecuaciones de Einstein. Oxford: Oxford University Press. pp. 37–39. ISBN 978-0-19-155226-7.OCLC 317496332 .
- ^ Siegel, Ethan (20 de mayo de 2016). «¿Cuándo fracasó finalmente Isaac Newton?». Forbes . Consultado el 3 de enero de 2017 .
- ^ Panofsky, Wolfgang K.; Phillips, Melba (2005). Electricidad y magnetismo clásicos (2.ª ed.). Mineola, NY: Dover Publ. ISBN 978-0-486-43924-2.
- ^ Zee, Anthony (2010). Teoría cuántica de campos en pocas palabras (2.ª ed.). Princeton University Press. pág. 29. ISBN 978-0-691-14034-6.
- ^ "fuerte, física 7.g" . Oxford English Dictionary (edición en línea). Oxford University Press . doi :10.1093/OED/1058721983. (Se requiere suscripción o membresía a una institución participante).
- ^ Stevens, Tab (10 de julio de 2003). «Quantum-Chromodynamics: A Definition – Science Articles». Archivado desde el original el 16 de octubre de 2011. Consultado el 4 de enero de 2008 .
- ^ Goldberg, Dave (2017). El modelo estándar en pocas palabras . Princeton University Press. ISBN 978-0-691-16759-6.
- ^ ab Greiner, Walter; Müller, Berndt; Greiner, Walter (2009). Teoría de calibre de interacciones débiles: con 75 ejemplos resueltos y ejercicios (4.ª ed.). Heidelberg: Springer. ISBN 978-3-540-87842-1.
- ^ Durrer, Ruth (2008). El fondo cósmico de microondas . Cambridge University Press. pp. 41–42. ISBN 978-0-521-84704-9.
Enlaces externos
- "Mecánica clásica, semana 2: Leyes de Newton". MIT OpenCourseWare . Consultado el 9 de agosto de 2023 .
- "Fundamentos de Física I, Lección 3: Leyes del movimiento de Newton". Cursos abiertos de Yale . Consultado el 9 de agosto de 2023 .




















































































