22 temperamento igual
En música, el temperamento igual 22 , llamado 22-TET, 22- EDO o 22-ET, es la escala temperada que se obtiene dividiendo la octava en 22 pasos iguales (razones de frecuencia iguales). Cada paso representa una razón de frecuencia de 22 √ 2 , o 54,55 centésimas ( ).
Al componer con 22-ET, hay que tener en cuenta una serie de consideraciones. Teniendo en cuenta el límite de 5 , hay una diferencia entre 3 quintas y la suma de 1 cuarta y 1 tercera mayor. Esto significa que, a partir de C, hay dos A: una a 16 pasos y otra a 17 pasos de distancia. También hay una diferencia entre un tono mayor y un tono menor. En C mayor, la segunda nota (D) estará a 4 pasos de distancia. Sin embargo, en A menor, donde A está 6 pasos por debajo de C, la cuarta nota (D) estará 9 pasos por encima de A, es decir, 3 pasos por encima de C. Por lo tanto, al cambiar de C mayor a A menor, es necesario cambiar ligeramente la nota D. Estas discrepancias surgen porque, a diferencia de 12-ET , 22-ET no suaviza la coma sintónica de 81/80, sino que exagera su tamaño al asignarla a un paso.
En el límite de 7 , la séptima menor septimal (7/4) se puede distinguir de la suma de una quinta (3/2) y una tercera menor (6/5), y la tercera submenor septimal (7/6) es diferente de la tercera menor (6/5). Esta asignación suaviza la coma septimal de 64/63, lo que permite que 22-ET funcione como un sistema "superpitagórico" donde cuatro quintas apiladas se equiparan con la tercera mayor septimal (9/7) en lugar de la tercera pental habitual de 5/4. Este sistema es una "imagen especular" del septimal halftone en muchos sentidos: los sistemas halftone afinan la quinta bemol de modo que los intervalos de 5 sean simples mientras que los intervalos de 7 sean complejos, los sistemas superpitagóricos tienen la quinta afinada sostenida de modo que los intervalos de 7 sean simples mientras que los intervalos de 5 sean complejos. La estructura enarmónica también se invierte: los sostenidos son más agudos que los bemoles, de forma similar a la afinación pitagórica (y por extensión al temperamento igual ), pero en mayor grado.
Finalmente, 22-ET tiene una buena aproximación del 11º armónico y, de hecho, es el temperamento igual más pequeño que es consistente en el límite 11 .
El efecto neto es que 22-ET permite (y hasta cierto punto incluso fuerza) la exploración de nuevos territorios musicales, al tiempo que mantiene excelentes aproximaciones a las consonancias de la práctica común.
Historia y uso
La idea de dividir la octava en 22 pasos de igual tamaño parece haberse originado con el teórico musical del siglo XIX RHM Bosanquet . Inspirado por el uso de una división desigual de la octava en 22 tonos en la teoría musical de la India , Bosanquet notó que una división igual de 22 tonos era capaz de representar música de 5 límites con una precisión tolerable. [1] En esto fue seguido en el siglo XX por el teórico José Würschmidt, quien lo señaló como un posible siguiente paso después del temperamento igual de 19 , y J. Murray Barbour en su estudio de la historia de la afinación, Tuning and Temperament . [2] Los defensores contemporáneos del temperamento igual de 22 incluyen al teórico musical Paul Erlich .
Notación


22-EDO se puede notar de varias formas. La primera, Ups And Downs Notation [3] , utiliza flechas hacia arriba y hacia abajo, escritas como un signo de intercalación y una "v" minúscula, generalmente en una fuente sans-serif. Una flecha equivale a un paso de nota. En los nombres de las notas, las flechas van primero, para facilitar la denominación de los acordes. Esto produce la siguiente escala cromática:
C, ^C/D ♭ , vC ♯ /^D ♭ , C ♯ /vD,
D, ^D/E ♭ , vD ♯ /^E ♭ , D ♯ /vE, E,
F, ^F/G ♭ , vF ♯ /^G ♭ , F ♯ /vG,
G, ^G/A ♭ , vG ♯ /^A ♭ , G ♯ /vA,
A, ^A/B ♭ , vA ♯ /^B ♭ , A ♯ /vB, B, C
El acorde pitagórico menor con 32/27 en C todavía se llama Cm y se escribe C–E ♭ –G. Pero el acorde menor ascendente con límite de 5 usa la tercera menor ascendente 6/5 y se escribe C–^E ♭ –G. Este acorde se llama C^m. Compárese con ^Cm (^C–^E ♭ –^G).
La segunda, la notación de cuarto de tono , utiliza medios sostenidos y medios bemoles en lugar de flechas hacia arriba y hacia abajo:
Sin embargo, los acordes y algunas equivalencias enarmónicas son muy diferentes a las de 12-EDO. Por ejemplo, aunque una tríada de Do menor con 5 límites se escribe como Do–Mi ♭ –Sol , las tríadas de Do mayor ahora se escriben como Do–Mi –G en lugar de C–E–G , y una tríada de La menor ahora es A–C
–G en lugar de C–E–G , y una tríada de La menor ahora es A–C –E aunque una tríada de A mayor sigue siendo A–C ♯ –E . Además, mientras que las segundas mayores como C–D se dividen como se espera en 4 cuartos de tono, las segundas menores como E–F y B–C son 1 cuarto de tono, no 2. Por lo tanto, E ♯ ahora es equivalente a F
–E aunque una tríada de A mayor sigue siendo A–C ♯ –E . Además, mientras que las segundas mayores como C–D se dividen como se espera en 4 cuartos de tono, las segundas menores como E–F y B–C son 1 cuarto de tono, no 2. Por lo tanto, E ♯ ahora es equivalente a F En lugar de F, F ♭ es equivalente a E
En lugar de F, F ♭ es equivalente a E En lugar de E, F es equivalente a E
En lugar de E, F es equivalente a E , y E es equivalente a F
, y E es equivalente a F Además, la nota una quinta por encima de B no es la esperada F ♯ sino F
Además, la nota una quinta por encima de B no es la esperada F ♯ sino F o G
o G , y la nota que está una quinta por debajo de F ahora es B
, y la nota que está una quinta por debajo de F ahora es B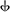 en lugar de B ♭ .
en lugar de B ♭ .
La tercera, la notación Porcupine, no introduce alteraciones accidentales nuevas, pero cambia significativamente la ortografía de los acordes (por ejemplo, la tríada mayor de 5 límites ahora es C–E ♯ –G ♯ ). Además, las equivalencias enarmónicas de 12-EDO ya no son válidas. Esto produce la siguiente escala cromática:
Do, Do ♯ , Re ♭ , Re , Re ♯ , Mi ♭ , Mi, Mi ♯ , Fa ♭ , Fa, Fa ♯, Sol ♭ , Sol, Sol ♯ , Sol /A
/A , A ♭ , A, A ♯ , B ♭ , B, B ♯ , C ♭ , C
, A ♭ , A, A ♯ , B ♭ , B, B ♯ , C ♭ , C
Tamaño del intervalo

La siguiente tabla muestra los tamaños de algunos intervalos comunes en el temperamento igual 22. Los intervalos que se muestran con un fondo sombreado, como los tritonos séptimales, están desafinados más de 1/4 de tono (aproximadamente 13,6 centésimas), en comparación con las proporciones justas a las que se aproximan.
| Nombre del intervalo | Tamaño (pasos) | Tamaño (centavos) | MIDI | Proporción justa | Sólo (centavos) | MIDI | Error (centavos) |
|---|---|---|---|---|---|---|---|
| octava | 22 | 1200 | 2:1 | 1200 | 0 | ||
| séptima mayor | 20 | 1090.91 | 15:8 | 1088.27 | + 0 2,64 | ||
| séptima menor septima | 18 | 981.818 | 7:4 | 968.82591 | + 0 12,99 | ||
| 17:10 amplia sexta mayor | 17 | 927.27 | 17:10 | 918.64 | + 0 8,63 | ||
| sexta mayor | 16 | 872,73 | 5:3 | 884.36 | -11,63 | ||
| quinta perfecta | 13 | 709.09 | 3:2 | 701,95 | + 0 7,14 | ||
| tritono septendecimal | 11 | 600,00 | 17:12 | 603.00 | - 0 3,00 | ||
| tritono | 11 | 600,00 | 45:32 | 590.22 | + 0 9,78 | ||
| tritono septimal | 11 | 600,00 | 7:5 | 582,51 | +17,49 | ||
| 11:8 cuarto ancho | 10 | 545,45 | 11:80 | 551.32 | - 0 5,87 | ||
| Subarmónico 375 | 10 | 545,45 | 512:375 | 539.10 | + 0 6,35 | ||
| 15:11 cuarto de ancho | 10 | 545,45 | 15:11 | 536,95 | + 0 8,50 | ||
| cuarta perfecta | 0 9 | 490,91 | 4:3 | 498.05 | − 0 7,14 | ||
| septendecimal supertercera mayor | 0 8 | 436.36 | 22:17 | 446,36 | −10,00 | ||
| septima tercera mayor | 0 8 | 436.36 | 9:7 | 435.08 | + 0 1,28 | ||
| cuarta disminuida | 0 8 | 436.36 | 32:25 | 427,37 | + 0 8,99 | ||
| tercera mayor indecimal | 0 8 | 436.36 | 14:11 | 417,51 | +18,86 | ||
| tercera mayor | 0 7 | 381,82 | 5:4 | 386.31 | − 0 4,49 | ||
| tercio neutro indecimal | 0 6 | 327,27 | 11:90 | 347,41 | -20,14 | ||
| tercio supramenor septendecimal | 0 6 | 327,27 | 17:14 | 336.13 | - 0 8,86 | ||
| tercera menor | 0 6 | 327,27 | 6:5 | 315,64 | +11,63 | ||
| septendecimal segundo aumentado | 0 5 | 272,73 | 20:17 | 281.36 | - 0 8,63 | ||
| segundo aumentado | 0 5 | 272,73 | 75:64 | 274,58 | - 0 1,86 | ||
| septimal tercera menor | 0 5 | 272,73 | 7:6 | 266,88 | + 0 5,85 | ||
| septimal tono entero | 0 4 | 218.18 | 8:7 | 231.17 | −12,99 | ||
| tercio disminuido | 0 4 | 218.18 | 256:225 | 223,46 | - 0 5,28 | ||
| septendecimal mayor segunda | 0 4 | 218.18 | 17:15 | 216,69 | + 0 1,50 | ||
| tono entero , tono mayor | 0 4 | 218.18 | 9:8 | 203,91 | +14,27 | ||
| tono entero, tono menor | 0 3 | 163,64 | 10:9 0 | 182,40 | -18,77 | ||
| Segundo neutro , mayor indecimal | 0 3 | 163,64 | 11:10 | 165,00 | - 0 1,37 | ||
| Armónico 1125 | 0 3 | 163,64 | 1125:1024 | 162,85 | + 0 0,79 | ||
| Segundo neutro, indecimal menor | 0 3 | 163,64 | 12:11 | 150,64 | +13.00 | ||
| semitono diatónico septimal | 0 2 | 109.09 | 15:14 | 119,44 | -10,35 | ||
| semitono diatónico , justo | 0 2 | 109.09 | 16:15 | 111,73 | - 0 2,64 | ||
| 17º armónico | 0 2 | 109.09 | 17:16 | 104,95 | + 0 4,13 | ||
| Dedo índice del laúd árabe | 0 2 | 109.09 | 18:17 | 0 98,95 | +10,14 | ||
| Semitono cromático septimal | 0 2 | 109.09 | 21:20 | 0 84,47 | +24,62 | ||
| semitono cromático , solo | 0 1 | 0 54,55 | 25:24 | 0 70,67 | -16,13 | ||
| septimal tercer tono | 0 1 | 0 54,55 | 28:27 | 0 62,96 | - 0 8,42 | ||
| cuarto de tono indecimal | 0 1 | 0 54,55 | 33:32 | 0 53,27 | + 0 1,27 | ||
| cuarto de tono septimal | 0 1 | 0 54,55 | 36:35 | 0 48,77 | + 0 5,78 | ||
| segundo disminuido | 0 1 | 0 54,55 | 128:125 | 0 41.06 | +13,49 |
Véase también
Referencias
- ^ Bosanquet, RHM "Sobre la división hindú de la octava, con adiciones a la teoría de órdenes superiores" (archivado el 22 de octubre de 2009), Actas de la Royal Society de Londres vol. 26 (1 de marzo de 1877 al 20 de diciembre de 1877) Taylor & Francis, Londres 1878, págs. 372-384. (Reproducido en Tagore, Sourindro Mohun, Música hindú de varios autores , Chowkhamba Sanskrit Series, Varanasi, India, 1965).
- ^ Barbour, James Murray, Afinación y temperamento, un estudio histórico , East Lansing, Michigan State College Press, 1953 [c1951].
- ^ "Notación de subidas y bajadas", en Xenharmonic Wiki . Consultado el 12 de agosto de 2023.
Enlaces externos
- Erlich, Paul, "Afinación, tonalidad y temperamento de veintidós tonos", William A. Sethares .
- Canon de Pachelbel en 22edo (MIDI), Herman Miller