Filtro de peine

En el procesamiento de señales , un filtro de peine es un filtro implementado añadiendo una versión retardada de una señal a sí mismo, lo que provoca interferencias constructivas y destructivas . La respuesta de frecuencia de un filtro de peine consiste en una serie de muescas espaciadas regularmente entre picos espaciados regularmente (a veces llamados dientes ) que dan la apariencia de un peine .
Los filtros de peine existen en dos formas, de avance y de retroalimentación , que se refieren a la dirección en la que se retrasan las señales antes de agregarse a la entrada.
Los filtros de peine se pueden implementar en formas de tiempo discreto o de tiempo continuo que son muy similares.
Aplicaciones

Los filtros de peine se emplean en una variedad de aplicaciones de procesamiento de señales, que incluyen:
- Filtros peine-integradores en cascada (CIC), comúnmente utilizados para suavizar el contraste durante operaciones de interpolación y diezmado que cambian la frecuencia de muestreo de un sistema de tiempo discreto.
- Los filtros de peine 2D y 3D implementados en hardware (y ocasionalmente en software) en decodificadores de televisión analógica PAL y NTSC reducen artefactos como el deslizamiento de puntos .
- Procesamiento de señales de audio , que incluye retardo , flanger , síntesis de modelado físico y síntesis de guía de ondas digitales . Si el retardo se establece en unos pocos milisegundos, un filtro de peine puede modelar el efecto de las ondas acústicas estacionarias en una cavidad cilíndrica o en una cuerda vibrante .
- En astronomía, el peine astronómico promete aumentar la precisión de los espectrógrafos existentes casi cien veces.
En acústica , el filtrado en peine puede surgir como un artefacto no deseado. Por ejemplo, dos altavoces que reproducen la misma señal a diferentes distancias del oyente crean un efecto de filtrado en peine en el audio. [1] En cualquier espacio cerrado, los oyentes escuchan una mezcla de sonido directo y sonido reflejado. El sonido reflejado toma un camino más largo y retrasado en comparación con el sonido directo, y se crea un filtro en peine donde los dos se mezclan en el oyente. [2] De manera similar, el filtrado en peine puede resultar de la mezcla mono de varios micrófonos, de ahí la regla general 3:1 de que los micrófonos vecinos deben estar separados al menos tres veces la distancia desde su fuente hasta el micrófono. [ cita requerida ]
Implementación de tiempo discreto
Formulario de retroalimentación

La estructura general de un filtro de peine de avance se describe mediante la ecuación diferencial :
donde es la longitud del retardo (medida en muestras) y α es un factor de escala aplicado a la señal retardada. La transformación z de ambos lados de la ecuación da como resultado:
La función de transferencia se define como:
Respuesta de frecuencia
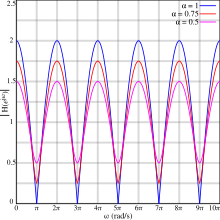

La respuesta de frecuencia de un sistema de tiempo discreto expresada en el dominio z se obtiene por sustitución donde es la unidad imaginaria y es la frecuencia angular . Por lo tanto, para el filtro peine de alimentación hacia adelante:
Usando la fórmula de Euler , la respuesta de frecuencia también viene dada por
A menudo resulta de interés la respuesta de magnitud , que ignora la fase. Esta se define como:
En el caso del filtro de peine de avance, esto es:
El término es constante, mientras que el término varía periódicamente . Por lo tanto, la respuesta de magnitud del filtro de peine es periódica.
Los gráficos muestran la respuesta de magnitud periódica para varios valores de algunas propiedades importantes:
- La respuesta cae periódicamente hasta un mínimo local (a veces conocido como muesca ) y aumenta periódicamente hasta un máximo local (a veces conocido como pico o diente ).
- Para valores positivos, el primer mínimo ocurre en la mitad del período de retardo y se repite en múltiplos pares de la frecuencia de retardo a partir de entonces:
- Los niveles de los máximos y mínimos son siempre equidistantes de 1.
- Cuando los mínimos tienen amplitud cero. En este caso, los mínimos se conocen a veces como nulos .
- Los máximos para valores positivos de coinciden con los mínimos para valores negativos de , y viceversa.
Respuesta al impulso
El filtro de peine de avance es uno de los filtros de respuesta de impulso finito más simples . [3] Su respuesta es simplemente el impulso inicial con un segundo impulso después del retraso.
Interpretación de polos y ceros
Volviendo a observar la función de transferencia del dominio z del filtro de peine de avance:
el numerador es igual a cero siempre que z K = − α . Esto tiene K soluciones, igualmente espaciadas alrededor de un círculo en el plano complejo ; estos son los ceros de la función de transferencia. El denominador es cero en z K = 0 , lo que da K polos en z = 0 . Esto conduce a un diagrama de polos y ceros como los que se muestran.
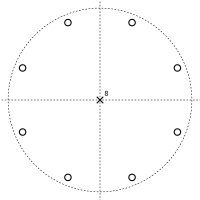 |  |
Formulario de comentarios

De manera similar, la estructura general de un filtro de peine de retroalimentación se describe mediante la ecuación diferencial :
Esta ecuación se puede reorganizar de modo que todos los términos estén en el lado izquierdo y luego tomar la transformada z :
La función de transferencia es por tanto:
Respuesta de frecuencia


Sustituyendo en la expresión del dominio z del filtro de peine de retroalimentación :
La respuesta de magnitud se convierte en:
Nuevamente, la respuesta es periódica, como lo demuestran los gráficos. El filtro peine de retroalimentación tiene algunas propiedades en común con la forma de retroalimentación anticipada:
- La respuesta cae periódicamente a un mínimo local y aumenta hasta un máximo local.
- Los máximos para valores positivos de coinciden con los mínimos para valores negativos de y viceversa.
- Para valores positivos, el primer máximo ocurre en 0 y se repite en múltiplos pares de la frecuencia de retardo a partir de entonces:
Sin embargo, también existen algunas diferencias importantes porque la respuesta de magnitud tiene un término en el denominador :
- Los niveles de los máximos y mínimos ya no son equidistantes de 1. Los máximos tienen una amplitud de 1/1 − α .
- El filtro sólo es estable si | α | es estrictamente menor que 1. Como se puede ver en los gráficos, a medida que | α | aumenta, la amplitud de los máximos aumenta cada vez más rápidamente.
Respuesta al impulso
El filtro de peine de retroalimentación es un tipo simple de filtro de respuesta de impulso infinito . [4] Si es estable, la respuesta simplemente consiste en una serie repetida de impulsos que disminuyen en amplitud con el tiempo.
Interpretación de polos y ceros
Volviendo a observar la función de transferencia del dominio z del filtro de peine de retroalimentación:
Esta vez, el numerador es cero en z K = 0 , lo que da K ceros en z = 0 . El denominador es igual a cero siempre que z K = α . Esto tiene K soluciones, igualmente espaciadas alrededor de un círculo en el plano complejo ; estos son los polos de la función de transferencia. Esto conduce a un gráfico de polos y ceros como los que se muestran a continuación.
Implementación de tiempo continuo
Los filtros de peine también pueden implementarse en tiempo continuo, lo que puede expresarse en el dominio de Laplace como una función del parámetro complejo del dominio de frecuencia análogo al dominio z. Los circuitos analógicos utilizan alguna forma de línea de retardo analógica para el elemento de retardo. Las implementaciones de tiempo continuo comparten todas las propiedades de las respectivas implementaciones de tiempo discreto.
Formulario de retroalimentación
La forma de propagación hacia adelante se puede describir mediante la ecuación:
donde τ es el retraso (medido en segundos). Esto tiene la siguiente función de transferencia:
La forma de propagación hacia adelante consiste en un número infinito de ceros espaciados a lo largo del eje jω ( que corresponde al dominio de Fourier ).
Formulario de comentarios
El formulario de comentarios tiene la ecuación:
y la siguiente función de transferencia:
La forma de retroalimentación consta de un número infinito de polos espaciados a lo largo del eje jω.
Véase también
Referencias
- ^ Roger Russell. "Audición, columnas y filtrado en peine" . Consultado el 22 de abril de 2010 .
- ^ "Conceptos básicos de acústica". Acoustic Sciences Corporation. Archivado desde el original el 7 de mayo de 2010.
- ^ Smith, JO "Filtros de peine de retroalimentación". Archivado desde el original el 6 de junio de 2011.
- ^ Smith, JO "Filtros de peine de retroalimentación". Archivado desde el original el 6 de junio de 2011.
![{\displaystyle y[n]=x[n]+\alpha x[nK]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/407d8d32def12f79789bde99eccb4d859fd98281)







![{\displaystyle H\left(e^{j\omega }\right)={\bigl [}1+\alpha \cos(\omega K){\bigr ]}-j\alpha \sin(\omega K)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a4500af1719c579363396c75f6f633b01eea232)










![{\displaystyle y[n]=x[n]+\alpha y[nK]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aab660dee16e819787a26d5de6162532f6da0da3)















