Construcción con regla y compás

Geometría
Proyectar una esfera a un plano
Describir Historia ( Cronología )
Sucursales Euclidiano No euclidiano Elíptico Esférico Hiperbólico Geometría no arquimediana Descriptivo Afín Sintético Analítico Algebraico Aritmética Diofántico Diferencial Riemanniano Simpléctico Diferencial discreto Complejo Finito Discreto/Combinatorio Digital Convexo Computacional Fractal Incidencia Geometría no conmutativa Geometría algebraica no conmutativa
Conceptos Características Dimensión Construcciones con regla y compás Ángulo Curva Diagonal Ortogonalidad ( perpendicular ) Paralelo Vértice Congruencia Semejanza Simetría
Cero-dimensional Punto
Unidimensional Línea segmento rayo Longitud
Bidimensional Avión Área Polígono Triángulo Altitud Hipotenusa Teorema de Pitágoras Paralelogramo Cuadrado Rectángulo Rombo Romboidal Cuadrilátero Trapecio Cometa Círculo Diámetro Circunferencia Área
Tridimensional Volumen Cubo cuboides Cilindro Dodecaedro Icosaedro Octaedro Pirámide Sólido platónico Esfera Tetraedro
Cuatro - / otras dimensiones Teseracto Hiperesfera
Geometrias
por nombre Aida Ariabhata Ahmes Alhazen Apolonio Arquímedes Atiyah Baudhayana Bolyai Brahma-upta Cartan Coxeter Descartes Euclides Euler Gauss Grómov Hilbert Huygens Jyeṣṭhadeva Katyayana Khayyám Pequeño Lobachevsky Manava Minkowski Minggatu Pascal Pitágoras Parameshvara Poincaré Riemann Sakabe Sijzi Al-Tusi Veblen Virasena Yang Hui Al-Yasamin Zhang Lista de geómetras
por periodo AEC Ahmes Baudhayana Manava Pitágoras Euclides Arquímedes Apolonio 1-1400 Zhang Katyayana Ariabhata Brahma-upta Virasena Alhazen Sijzi Khayyám Al-Yasamin Al-Tusi Yang Hui Parameshvara Década de 1400–1700 Jyeṣṭhadeva Descartes Pascal Huygens Minggatu Euler Sakabe Aida Década de 1700 a 1900 Gauss Lobachevsky Bolyai Riemann Pequeño Poincaré Hilbert Minkowski Cartan Veblen Coxeter En la actualidad Atiyah Grómov
en a mi

En geometría , la construcción con regla y compás , también conocida como construcción con regla y compás , construcción euclidiana o construcción clásica , es la construcción de longitudes, ángulos y otras figuras geométricas utilizando únicamente una regla idealizada y un par de compases .

Se supone que la regla idealizada, conocida como regla de borde recto , tiene una longitud infinita, un solo borde y no tiene marcas. Se supone que el compás no tiene radio máximo ni mínimo y que "colapsa" cuando se levanta de la página, por lo que no se puede usar directamente para transferir distancias. (Esta es una restricción sin importancia ya que, utilizando un procedimiento de varios pasos, se puede transferir una distancia incluso con un compás colapsable; consulte el teorema de equivalencia del compás . Sin embargo, tenga en cuenta que, si bien un compás no colapsable sostenido contra una regla puede parecer equivalente a marcarlo, la construcción neusis sigue siendo inadmisible y esto es lo que realmente significa sin marcar: consulte Reglas marcables a continuación). Más formalmente, las únicas construcciones permisibles son las otorgadas por los primeros tres postulados de los Elementos de Euclides .

Resulta ser el caso que cada punto construible usando regla y compás también puede construirse usando solo compás , o solo con regla si se da un solo círculo y su centro.

Los matemáticos de la antigua Grecia fueron los primeros en concebir construcciones con regla y compás, y varios problemas antiguos de geometría plana imponen esta restricción. Los antiguos griegos desarrollaron muchas construcciones, pero en algunos casos no pudieron hacerlo. Gauss demostró que algunos polígonos son construibles pero que la mayoría no lo son. Pierre Wantzel demostró en 1837 que algunos de los problemas más famosos con regla y compás eran imposibles de construir utilizando la teoría de campos , a saber, trisecar un ángulo arbitrario y duplicar el volumen de un cubo (véase § construcciones imposibles). Muchos de estos problemas son fácilmente solucionables siempre que se permitan otras transformaciones geométricas; por ejemplo, la construcción de neusis se puede utilizar para resolver los dos problemas anteriores.

En términos de álgebra , una longitud es construible si y solo si representa un número construible , y un ángulo es construible si y solo si su coseno es un número construible. Un número es construible si y solo si se puede escribir utilizando las cuatro operaciones aritméticas básicas y la extracción de raíces cuadradas , pero no de raíces de orden superior.

La "regla" y el "compás" de las construcciones con regla y compás son versiones idealizadas de reglas y compases del mundo real .

• La regla es un borde infinitamente largo que no tiene marcas. Solo se puede utilizar para dibujar un segmento de línea entre dos puntos o para extender un segmento de línea existente.
• El compás puede tener un radio arbitrario sin marcas (a diferencia de ciertas brújulas del mundo real). Se pueden dibujar círculos y arcos circulares a partir de dos puntos dados: el centro y un punto del círculo. El compás puede o no colapsar (es decir, doblarse después de sacarlo de la página, borrando su radio "almacenado").
• Las líneas y círculos construidos tienen precisión infinita y ancho cero.

Las brújulas actuales no colapsan y las construcciones geométricas modernas a menudo utilizan esta característica. Una "brújula colapsable" parecería ser un instrumento menos poderoso. Sin embargo, según el teorema de equivalencia de brújulas de la Proposición 2 del Libro 1 de los Elementos de Euclides , no se pierde potencia al utilizar una brújula colapsable. Aunque la proposición es correcta, sus demostraciones tienen una larga y accidentada historia. ^[1] En cualquier caso, la equivalencia es la razón por la que esta característica no está estipulada en la definición de la brújula ideal.

Cada construcción debe ser matemáticamente exacta . No se permite calcular distancias a simple vista (mirar la construcción y adivinar su precisión) ni usar marcas en una regla. Cada construcción también debe terminar en . Es decir, debe tener un número finito de pasos y no ser el límite de aproximaciones cada vez más cercanas. (Si se permite un número ilimitado de pasos, algunas construcciones que de otro modo serían imposibles se vuelven posibles por medio de secuencias infinitas que convergen hacia un límite ).

Planteadas de esta manera, las construcciones con regla y compás parecen ser un juego de salón , más que un problema práctico serio; pero el propósito de la restricción es asegurar que se pueda demostrar que las construcciones son exactamente correctas.

Los matemáticos griegos antiguos intentaron primero realizar construcciones con regla y compás, y descubrieron cómo construir sumas , diferencias , productos , razones y raíces cuadradas de longitudes dadas. ^{[2] : p. 1} También podían construir la mitad de un ángulo dado , un cuadrado cuya área es el doble de la de otro cuadrado, un cuadrado que tiene la misma área que un polígono dado y polígonos regulares de 3, 4 o 5 lados ^{[2] : p. xi} (o uno con el doble del número de lados de un polígono dado ^{[2] : pp. 49-50} ). Pero no podían construir un tercio de un ángulo dado excepto en casos particulares, o un cuadrado con la misma área que un círculo dado , o polígonos regulares con otros números de lados. ^{[2] : p. xi} Tampoco podían construir el lado de un cubo cuyo volumen es el doble del volumen de un cubo con un lado dado. ^{[2] : p. 29}

Hipócrates y Menecmo demostraron que el volumen del cubo se podía duplicar hallando las intersecciones de hipérbolas y parábolas , pero éstas no se pueden construir con regla y compás. ^{[2] : p. 30} En el siglo V a. C., Hipias utilizó una curva que llamó cuadratriz para trisecar el ángulo general y cuadrar el círculo, y Nicomedes en el siglo II a. C. mostró cómo utilizar una concoide para trisecar un ángulo arbitrario; ^{[2] : p. 37} pero estos métodos tampoco se pueden seguir solo con regla y compás.

Durante dos milenios no se hizo ningún progreso en los problemas no resueltos, hasta que en 1796 Gauss demostró que se podía construir un polígono regular con 17 lados; cinco años más tarde demostró el criterio suficiente para que se pudiera construir un polígono regular de n lados. ^{[2] : págs. 51 y siguientes.}

En 1837 Pierre Wantzel publicó una prueba de la imposibilidad de trisecar un ángulo arbitrario o de duplicar el volumen de un cubo, ^[3] basándose en la imposibilidad de construir raíces cúbicas de longitudes. También demostró que la condición de constructibilidad suficiente de Gauss para polígonos regulares también es necesaria. ^[4]

Luego, en 1882, Lindemann demostró que es un número trascendental y, por lo tanto, es imposible construir con regla y compás un cuadrado con la misma área que un círculo dado. ^{[2] : p. 47}${\displaystyle \pi }$

Todas las construcciones con regla y compás consisten en la aplicación repetida de cinco construcciones básicas utilizando los puntos, líneas y círculos que ya se han construido. Son:

• Creando la línea a través de dos puntos
• Creando el círculo que contiene un punto y tiene un centro en otro punto
• Creando el punto en la intersección de dos líneas (no paralelas)
• Creación de uno o dos puntos en la intersección de una línea y un círculo (si se cruzan)
• Creando uno o dos puntos en la intersección de dos círculos (si se intersecan).

Por ejemplo, partiendo de dos puntos distintos, podemos crear una línea o cualquiera de dos círculos (a su vez, utilizando cada punto como centro y pasando por el otro punto). Si dibujamos ambos círculos, se crean dos nuevos puntos en sus intersecciones. Trazando líneas entre los dos puntos originales y uno de estos nuevos puntos se completa la construcción de un triángulo equilátero.

Por tanto, en cualquier problema geométrico tenemos un conjunto inicial de símbolos (puntos y líneas), un algoritmo y unos resultados. Desde esta perspectiva, la geometría equivale a un álgebra axiomática , sustituyendo sus elementos por símbolos. Probablemente Gauss fue el primero en darse cuenta de esto, y lo utilizó para demostrar la imposibilidad de algunas construcciones; solo mucho más tarde Hilbert encontró un conjunto completo de axiomas para la geometría .

Las construcciones con regla y compás más utilizadas incluyen:

• Construir la bisectriz perpendicular a partir de un segmento
• Encontrar el punto medio de un segmento.
• Dibujar una línea perpendicular desde un punto a una línea.
• Bisecar un ángulo
• Reflejar un punto en una línea
• Construir una línea a través de un punto tangente a un círculo
• Construcción de un círculo a través de 3 puntos no colineales
• Trazar una línea a través de un punto dado paralela a una línea dada.

Construcciones con regla y compás correspondientes a operaciones algebraicas

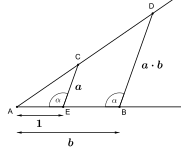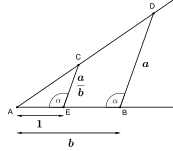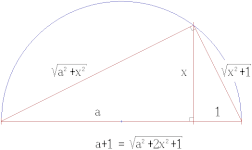Podemos asociar un álgebra a nuestra geometría utilizando un sistema de coordenadas cartesianas formado por dos líneas y representar puntos de nuestro plano mediante vectores . Finalmente podemos escribir estos vectores como números complejos.

Utilizando las ecuaciones para líneas y círculos, se puede demostrar que los puntos en los que se intersecan se encuentran en una extensión cuadrática del campo más pequeño F que contiene dos puntos en la línea, el centro del círculo y el radio del círculo. Es decir, tienen la forma , donde x , y y k están en F .${\displaystyle x+y={\sqrt {k}}}$

Como el campo de puntos construibles está cerrado bajo raíces cuadradas , contiene todos los puntos que pueden obtenerse mediante una secuencia finita de extensiones cuadráticas del campo de números complejos con coeficientes racionales. Por el párrafo anterior, se puede demostrar que cualquier punto construible puede obtenerse mediante dicha secuencia de extensiones. Como corolario de esto, se encuentra que el grado del polinomio mínimo para un punto construible (y por lo tanto de cualquier longitud construible) es una potencia de 2. En particular, cualquier punto (o longitud) construible es un número algebraico , aunque no todo número algebraico es construible; por ejemplo, ³ √ 2 es algebraico pero no construible. ^[3]

Existe una biyección entre los ángulos que son construibles y los puntos que son construibles en cualquier círculo construible. Los ángulos que son construibles forman un grupo abeliano bajo la adición módulo 2π (que corresponde a la multiplicación de los puntos en el círculo unitario vistos como números complejos). Los ángulos que son construibles son exactamente aquellos cuya tangente (o equivalentemente, seno o coseno) es construible como un número. Por ejemplo, el heptadecágono regular (el polígono regular de diecisiete lados ) es construible porque

${\displaystyle {\begin{aligned}\cos {\left({\frac {2\pi }{17}}\right)}&=\,-{\frac {1}{16}}\,+\,{\frac {1}{16}}{\sqrt {17}}\,+\,{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\\[5mu]&\qquad +\,{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}\end{aligned}}}$

como lo descubrió Gauss . ^[5]

El grupo de ángulos construibles está cerrado por la operación de dividir los ángulos por la mitad (que corresponde a sacar raíces cuadradas en los números complejos). Los únicos ángulos de orden finito que se pueden construir a partir de dos puntos son aquellos cuyo orden es o bien una potencia de dos, o bien un producto de una potencia de dos por un conjunto de primos de Fermat distintos . Además, existe un conjunto denso de ángulos construibles de orden infinito.

Dado un conjunto de puntos en el plano euclidiano , seleccionar cualquiera de ellos para llamarlo 0 y otro para llamarlo 1 , junto con una elección arbitraria de orientación, nos permite considerar los puntos como un conjunto de números complejos .

Dada cualquier interpretación de un conjunto de puntos como números complejos, los puntos construibles utilizando únicamente construcciones válidas con regla y compás son precisamente los elementos del campo más pequeño que contiene el conjunto original de puntos y está cerrado bajo las operaciones de conjugado complejo y raíz cuadrada (para evitar ambigüedades, podemos especificar la raíz cuadrada con argumento complejo menor que π). Los elementos de este campo son precisamente aquellos que pueden expresarse como una fórmula en los puntos originales utilizando únicamente las operaciones de suma , resta , multiplicación , división , conjugado complejo y raíz cuadrada , que se ve fácilmente como un subconjunto denso contable del plano. Cada una de estas seis operaciones corresponde a una construcción simple con regla y compás. A partir de una fórmula de este tipo, es sencillo producir una construcción del punto correspondiente combinando las construcciones para cada una de las operaciones aritméticas. Las construcciones más eficientes de un conjunto particular de puntos corresponden a atajos en tales cálculos.

De manera equivalente (y sin necesidad de elegir arbitrariamente dos puntos) podemos decir que, dada una elección arbitraria de orientación, un conjunto de puntos determina un conjunto de razones complejas dado por las razones de las diferencias entre dos pares de puntos cualesquiera. El conjunto de razones que se puede construir usando regla y compás a partir de dicho conjunto de razones es precisamente el cuerpo más pequeño que contiene las razones originales y que se cierra tomando conjugados complejos y raíces cuadradas.

Por ejemplo, la parte real, la parte imaginaria y el módulo de un punto o relación z (tomando uno de los dos puntos de vista anteriores) son construibles ya que pueden expresarse como

${\displaystyle \mathrm {Re} (z)={\frac {z+{\bar {z}}}{2}}\;}$

${\displaystyle \mathrm {Im} (z)={\frac {z-{\bar {z}}}{2i}}\;}$

${\displaystyle \left|z\right|={\sqrt {z{\bar {z}}}}.\;}$

La duplicación del cubo y la trisección de un ángulo (excepto los ángulos especiales como cualquier φ tal que φ /(2 π )) es un número racional con denominador no divisible por 3) requieren razones que sean la solución de ecuaciones cúbicas , mientras que la cuadratura del círculo requiere una razón trascendental . Ninguna de estas se encuentra en los campos descritos, por lo tanto, no existe una construcción con regla y compás para estas.

Los antiguos griegos pensaban que los problemas de construcción que no podían resolver eran simplemente obstinados, no irresolubles. ^[6] Sin embargo, con los métodos modernos, se ha demostrado que estas construcciones con regla y compás son lógicamente imposibles de realizar. (Sin embargo, los problemas en sí mismos son solucionables, y los griegos sabían cómo resolverlos sin la restricción de trabajar solo con regla y compás).

El más famoso de estos problemas, la cuadratura del círculo , también conocida como cuadratura del círculo, implica construir un cuadrado con la misma área que un círculo dado utilizando únicamente regla y compás.

Se ha demostrado que la cuadratura del círculo es imposible, ya que implica generar un número trascendente , es decir, √ π . Solo ciertos números algebraicos se pueden construir con regla y compás únicamente, es decir, aquellos construidos a partir de los números enteros con una secuencia finita de operaciones de suma, resta, multiplicación, división y extracción de raíces cuadradas. La frase "cuadratura del círculo" se utiliza a menudo para significar "hacer lo imposible" por esta razón.

Sin la restricción de requerir una solución únicamente con regla y compás, el problema se puede resolver fácilmente mediante una amplia variedad de medios geométricos y algebraicos, y se resolvió muchas veces en la antigüedad. ^[7]

Un método que se acerca mucho a la "cuadratura del círculo" se puede lograr utilizando un triángulo de Kepler .

La duplicación del cubo es la construcción, utilizando únicamente una regla y un compás, de la arista de un cubo que tiene el doble del volumen de un cubo con una arista dada. Esto es imposible porque la raíz cúbica de 2, aunque algebraica, no se puede calcular a partir de números enteros mediante suma, resta, multiplicación, división y extracción de raíces cuadradas. Esto se deduce de que su polinomio mínimo sobre los racionales tiene grado 3. Esta construcción es posible utilizando una regla con dos marcas y un compás.

La trisección de un ángulo es la construcción, utilizando únicamente una regla y un compás, de un ángulo que es un tercio de un ángulo arbitrario dado. Esto es imposible en el caso general. Por ejemplo, el ángulo 2 π /5 radianes (72° = 360°/5) se puede trisecar, pero el ángulo de π /3 radianes (60 ° ) no se puede trisecar. ^[8] El problema general de la trisección también se resuelve fácilmente cuando se permite una regla con dos marcas (una construcción de neusis ).

El segmento de línea desde cualquier punto en el plano hasta el punto más cercano en un círculo se puede construir, pero el segmento desde cualquier punto en el plano hasta el punto más cercano en una elipse de excentricidad positiva no se puede construir en general. Véase ^[9] Nótese que los resultados demostrados aquí son en su mayoría una consecuencia de la no constructividad de las cónicas. Si la cónica inicial se considera como un hecho, entonces la prueba debe revisarse para verificar si es necesario generar otra cónica distinta. Como ejemplo, se conocen construcciones para normales de una parábola, pero necesitan usar una intersección entre el círculo y la parábola misma. Por lo tanto, no son construibles en el sentido de que la parábola no es construible.

En 1997, el matemático de Oxford Peter M. Neumann demostró el teorema de que no existe una construcción con regla y compás para la solución general del antiguo problema de Alhazen (problema de billar o reflexión en un espejo esférico). ^{[10] [11]}

Algunos polígonos regulares (por ejemplo, un pentágono ) son fáciles de construir con regla y compás; otros no. Esto llevó a la pregunta: ¿Es posible construir todos los polígonos regulares con regla y compás?

Carl Friedrich Gauss demostró en 1796 que se puede construir un polígono regular de 17 lados, y cinco años después demostró que se puede construir un polígono regular de n lados con regla y compás si los factores primos impares de n son primos de Fermat distintos . Gauss conjeturó que esta condición también era necesaria ; la conjetura fue demostrada por Pierre Wantzel en 1837. ^[4]

Los primeros polígonos regulares construibles tienen los siguientes números de lados:

3 , 4 , 5 , 6 , 8 , 10 , 12 , 15 , 16 , 17 , 20 , 24 , 30 , 32 , 34 , 40 , 48 , 51, 60 , 64 , 68, 80 , 85, 96 , 102, 120 , 128, 136, 160, 170, 192, 204, 240, 255, 256, 257 , 272... (secuencia A003401 en la OEIS )

Se sabe que hay una infinidad de polígonos regulares construibles con un número par de lados (porque si un n -gono regular es construible, entonces también lo es un 2 - gono regular y, por lo tanto, un 4 - gono regular, un 8 - gono regular, etc.). Sin embargo, solo hay 5 primos de Fermat conocidos, lo que da solo 31 n -gonos regulares construibles conocidos con un número impar de lados.

Dieciséis puntos clave de un triángulo son sus vértices , los puntos medios de sus lados , los pies de sus alturas , los pies de las bisectrices de sus ángulos internos y su circuncentro , baricentro , ortocentro e incentro . Estos pueden tomarse de tres en tres para producir 139 problemas no triviales distintos de construcción de un triángulo a partir de tres puntos. ^[12] De estos problemas, tres involucran un punto que puede construirse de manera única a partir de los otros dos puntos; 23 pueden construirse de manera no única (de hecho, para infinitas soluciones) pero solo si las ubicaciones de los puntos obedecen a ciertas restricciones; en 74 el problema es construible en el caso general; y en 39 el triángulo requerido existe pero no es construible.

Las doce longitudes clave de un triángulo son las tres longitudes de los lados, las tres alturas , las tres medianas y las tres bisectrices de los ángulos . Junto con los tres ángulos, estas dan lugar a 95 combinaciones distintas, 63 de las cuales dan lugar a un triángulo construible, 30 de las cuales no, y dos de las cuales están indefinidas. ^{[13] : págs. 201–203}

Se han realizado varios intentos para restringir las herramientas permitidas para las construcciones bajo diversas reglas, con el fin de determinar qué es todavía construible y cómo se puede construir, así como determinar los criterios mínimos necesarios para poder seguir construyendo todo lo que se puede construir con compás y regla.

Es posible (según el teorema de Mohr-Mascheroni ) construir cualquier cosa con solo un compás si se puede construir con una regla y un compás, siempre que los datos dados y los datos que se deben encontrar consistan en puntos discretos (no líneas o círculos). La verdad de este teorema depende de la verdad del axioma de Arquímedes ^[14] , que no es de primer orden por naturaleza. Entre los ejemplos de construcciones con solo compás se incluye el problema de Napoleón .

Es imposible sacar una raíz cuadrada sólo con una regla, por lo que algunas cosas que no se pueden construir con una regla se pueden construir con un compás; pero (por el teorema de Poncelet-Steiner ) dado un solo círculo y su centro, se pueden construir.

Los antiguos griegos clasificaban las construcciones en tres categorías principales, dependiendo de la complejidad de las herramientas necesarias para su solución. Si una construcción utilizaba solo una regla y un compás, se llamaba plana; si también requería una o más secciones cónicas (distintas del círculo), entonces se llamaba sólida; la tercera categoría incluía todas las construcciones que no caían en ninguna de las otras dos categorías. ^[15] Esta categorización encaja bien con el punto de vista algebraico moderno. Un número complejo que se puede expresar utilizando solo las operaciones de campo y las raíces cuadradas (como se describió anteriormente) tiene una construcción plana. Un número complejo que incluye también la extracción de raíces cúbicas tiene una construcción sólida.

En el lenguaje de los cuerpos, un número complejo que es plano tiene grado de potencia de dos y se encuentra en una extensión de cuerpo que se puede descomponer en una torre de cuerpos donde cada extensión tiene grado dos. Un número complejo que tiene una construcción sólida tiene grado con factores primos de solo dos y tres, y se encuentra en una extensión de cuerpo que está en la parte superior de una torre de cuerpos donde cada extensión tiene grado 2 o 3.

Un punto tiene una construcción sólida si se puede construir utilizando una regla, un compás y una herramienta de dibujo de cónicas (posiblemente hipotética) que pueda dibujar cualquier cónica con foco, directriz y excentricidad ya construidos. El mismo conjunto de puntos a menudo se puede construir utilizando un conjunto más pequeño de herramientas. Por ejemplo, utilizando un compás, una regla y un trozo de papel en el que tenemos la parábola y=x ² junto con los puntos (0,0) y (1,0), se puede construir cualquier número complejo que tenga una construcción sólida. Del mismo modo, una herramienta que pueda dibujar cualquier elipse con focos y ejes mayores ya construidos (piense en dos alfileres y un trozo de cuerda) es igualmente poderosa. ^[16]

Los antiguos griegos sabían que tanto la duplicación del cubo como la trisección de un ángulo arbitrario tenían construcciones sólidas. Arquímedes dio una construcción neusis del heptágono regular , que fue interpretada por los comentaristas árabes medievales, Bartel Leendert van der Waerden y otros como basada en una construcción sólida, pero esto ha sido discutido, ya que son posibles otras interpretaciones. ^[17] La ​​cuadratura del círculo no tiene una construcción sólida.

Un n -gono regular tiene una construcción sólida si y solo si n = 2 ^a 3 ^b m donde a y b son algunos números enteros no negativos y m es un producto de cero o más primos de Pierpont distintos (primos de la forma 2 ^r 3 ^s +1). Por lo tanto, un n -gono regular admite una construcción sólida, pero no plana, si y solo si n está en la secuencia

7 , 9 , 13 , 14 , 18 , 19 , 21 , 26, 27, 28, 35, 36, 37, 38, 39, 42 , 45, 52, 54, 56, 57, 63, 65, 70, 72, 73, 74, 76, 78, 81, 84, 90, 91, 95, 97... (secuencia A051913 en la OEIS )

El conjunto de n para el cual un n -gono regular no tiene construcción sólida es la secuencia

11 , 22 , 23 , 25, 29, 31, 33, 41, 43, 44, 46, 47, 49, 50, 53, 55, 58, 59, 61, 62, 66, 67, 69, 71, 75, 77, 79, 82, 83, 86, 87, 88, 89, 92, 93, 94, 98, 99, 100... (secuencia A048136 en la OEIS )

Al igual que la cuestión de los primos de Fermat, es una pregunta abierta si hay un número infinito de primos de Pierpont.

¿Qué pasaría si, junto con la regla y el compás, tuviéramos una herramienta que (solo) pudiera trisecar un ángulo arbitrario? Tales construcciones son construcciones sólidas, pero existen números con construcciones sólidas que no pueden construirse utilizando tal herramienta. Por ejemplo, no podemos duplicar el cubo con tal herramienta. ^[18] Por otro lado, cada n-gono regular que tenga una construcción sólida puede construirse utilizando tal herramienta.

La teoría matemática del origami es más poderosa que la construcción con regla y compás. Los pliegues que satisfacen los axiomas de Huzita-Hatori pueden construir exactamente el mismo conjunto de puntos que las construcciones extendidas utilizando un compás y una herramienta de dibujo cónico. Por lo tanto, el origami también se puede utilizar para resolver ecuaciones cúbicas (y, por lo tanto, ecuaciones cuárticas) y, por lo tanto, resolver dos de los problemas clásicos. ^[19]

Arquímedes , Nicomedes y Apolonio dieron construcciones que implicaban el uso de una regla marcable. Esto les permitiría, por ejemplo, tomar un segmento de línea, dos líneas (o círculos) y un punto; y luego dibujar una línea que pase por el punto dado e intersecta las dos líneas dadas, de modo que la distancia entre los puntos de intersección sea igual al segmento dado. Los griegos llamaron a esto neusis ("inclinación", "tendencia" o "vergencia"), porque la nueva línea tiende al punto. En este esquema ampliado, podemos trisecar un ángulo arbitrario (ver la trisección de Arquímedes) o extraer una raíz cúbica arbitraria (debido a Nicomedes). Por lo tanto, cualquier distancia cuya razón con una distancia existente sea la solución de una ecuación cúbica o cuártica es construible. Usando una regla marcable, los polígonos regulares con construcciones sólidas, como el heptágono , son construibles; y John H. Conway y Richard K. Guy dan construcciones para varios de ellos. ^[20]

La construcción de neusis es más poderosa que una herramienta de dibujo cónico, ya que se pueden construir números complejos que no tienen construcciones sólidas. De hecho, utilizando esta herramienta se pueden resolver algunos quinticos que no son solucionables utilizando radicales . ^[21] Se sabe que no se puede resolver un polinomio irreducible de grado primo mayor o igual a 7 utilizando la construcción de neusis, por lo que no es posible construir un 23-gono o 29-gono regular utilizando esta herramienta. Benjamin y Snyder demostraron que es posible construir el 11-gono regular, pero no dieron una construcción. ^[22] Todavía está abierto si un 25-gono o 31-gono regular es construible utilizando esta herramienta.

Dado un segmento de línea recta llamado AB, ¿podría este dividirse en tres nuevos segmentos iguales y en tantas partes como se requiere mediante el uso del teorema de intersección ?

En 1998, Simon Plouffe presentó un algoritmo de regla y compás que puede utilizarse para calcular dígitos binarios de ciertos números. ^[23] El algoritmo implica la duplicación repetida de un ángulo y se vuelve físicamente impráctico después de unos 20 dígitos binarios.

• Círculo de Carlyle
• Criptografía geométrica
• Geometrografía
• Lista de software de geometría interactiva , la mayoría de ellos muestran construcciones con regla y compás.
• Matemáticas del plegado de papel
• Underwood Dudley , un matemático que ha hecho de su actividad secundaria la recopilación de pruebas falsas hechas con regla y compás.

• Construcciones de polígonos regulares por el Dr. Math en The Math Forum @ Drexel
• Construcción con la brújula Solo en cut-the-knot
• Trisección de ángulos de Hipócrates en Cut-the-Knot
• Weisstein, Eric W. "Trisección de ángulos". MundoMatemático .