Ondícula

Una wavelet es una oscilación similar a una onda con una amplitud que comienza en cero, aumenta o disminuye y luego vuelve a cero una o más veces. Las wavelets se denominan "oscilaciones breves". Se ha establecido una taxonomía de wavelets, basada en el número y la dirección de sus pulsos. Las wavelets están imbuidas de propiedades específicas que las hacen útiles para el procesamiento de señales .

Por ejemplo, se podría crear una wavelet con una frecuencia de do central y una duración corta de aproximadamente una décima de segundo. Si esta wavelet se convolucionara con una señal creada a partir de la grabación de una melodía, la señal resultante sería útil para determinar cuándo apareció la nota do central en la canción. Matemáticamente, una wavelet se correlaciona con una señal si una parte de la señal es similar. La correlación es el núcleo de muchas aplicaciones prácticas de wavelet.

Como herramienta matemática, los wavelets se pueden utilizar para extraer información de muchos tipos de datos, incluidas señales de audio e imágenes. Se necesitan conjuntos de wavelets para analizar los datos en su totalidad. Los wavelets "complementarios" descomponen una señal sin espacios ni superposiciones, de modo que el proceso de descomposición es matemáticamente reversible. Por lo tanto, los conjuntos de wavelets complementarios son útiles en algoritmos de compresión/descompresión basados ​​en wavelets , donde es deseable recuperar la información original con una pérdida mínima.

En términos formales, esta representación es una representación en serie de ondículas de una función integrable al cuadrado con respecto a un conjunto completo y ortonormal de funciones base o a un conjunto sobrecompleto o marco de un espacio vectorial , para el espacio de Hilbert de funciones integrables al cuadrado. Esto se logra a través de estados coherentes .

En física clásica , el fenómeno de difracción se describe mediante el principio de Huygens-Fresnel , que trata cada punto de un frente de onda en propagación como una colección de ondículas esféricas individuales. ^[1] El patrón de curvatura característico es más pronunciado cuando una onda de una fuente coherente (como un láser) encuentra una rendija/abertura que es comparable en tamaño a su longitud de onda . Esto se debe a la adición, o interferencia , de diferentes puntos en el frente de onda (o, equivalentemente, cada ondícula) que viajan por caminos de diferentes longitudes hasta la superficie de registro. Múltiples aberturas estrechamente espaciadas (por ejemplo, una rejilla de difracción ) pueden dar como resultado un patrón complejo de intensidad variable.

La palabra wavelet se ha utilizado durante décadas en el procesamiento de señales digitales y en la geofísica de exploración. ^[2] La palabra francesa equivalente ondelette, que significa "onda pequeña", fue utilizada por Jean Morlet y Alex Grossmann a principios de la década de 1980.

Esta sección no cita ninguna fuente . Por favor, ayude a mejorar esta sección añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado . ( Noviembre de 2014 ) ( Aprenda cómo y cuándo eliminar este mensaje )

La teoría de wavelets es aplicable a varios temas. Todas las transformadas wavelet pueden considerarse formas de representación tiempo-frecuencia para señales de tiempo continuo (analógicas) y, por lo tanto, están relacionadas con el análisis armónico . La transformada wavelet discreta (continua en el tiempo) de una señal de tiempo discreto (muestreada) mediante el uso de bancos de filtros de tiempo discreto de configuración diádica (banda de octava) es una aproximación wavelet a esa señal. Los coeficientes de dicho banco de filtros se denominan coeficientes de desplazamiento y escala en la nomenclatura de wavelets. Estos bancos de filtros pueden contener filtros de respuesta de impulso finito (FIR) o de respuesta de impulso infinito (IIR). Las wavelets que forman una transformada wavelet continua (CWT) están sujetas al principio de incertidumbre de la teoría de muestreo respectiva del análisis de Fourier: dada una señal con algún evento en ella, no se puede asignar simultáneamente una escala de respuesta de tiempo y frecuencia exacta a ese evento. El producto de las incertidumbres de la escala de respuesta de tiempo y frecuencia tiene un límite inferior. Por lo tanto, en el escaleograma de una transformada wavelet continua de esta señal, dicho evento marca una región entera en el plano de escala temporal, en lugar de solo un punto. Además, las bases wavelet discretas pueden considerarse en el contexto de otras formas del principio de incertidumbre. ^{[3] [4] [5] [6]}

Las transformadas wavelet se dividen en tres clases: continuas, discretas y basadas en múltiples resoluciones.

En las transformadas wavelet continuas , una señal dada de energía finita se proyecta en una familia continua de bandas de frecuencia (o subespacios similares del espacio de funciones L ^p L ² ( R ) ). Por ejemplo, la señal puede representarse en cada banda de frecuencia de la forma [ f , 2 f ] para todas las frecuencias positivas f > 0. Luego, la señal original puede reconstruirse mediante una integración adecuada sobre todos los componentes de frecuencia resultantes.

Las bandas de frecuencia o subespacios (subbandas) son versiones escaladas de un subespacio a escala 1. Este subespacio a su vez se genera en la mayoría de las situaciones por los desplazamientos de una función generadora ψ en L ² ( R ), la wavelet madre . Para el ejemplo de la banda de frecuencia de escala uno [1, 2] esta función es con la función sinc (normalizada) . Ése, el de Meyer y otros dos ejemplos de wavelets madre son:$${\displaystyle \psi (t)=2\,\nombre del operador {sinc} (2t)-\,\nombre del operador {sinc} (t)={\frac {\sin(2\pi t)-\sin(\pi t)}{\pi t}}}$$

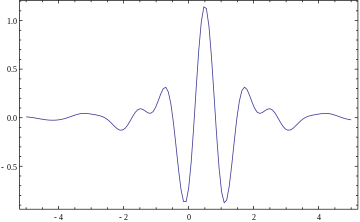El subespacio de escala a o banda de frecuencia [1/ a , 2/ a ] se genera mediante las funciones (a veces llamadas wavelets hijas ) donde a es positivo y define la escala y b es cualquier número real y define el desplazamiento. El par ( a , b ) define un punto en el semiplano derecho R ₊ × R .$${\displaystyle \psi_{a,b}(t)={\frac {1}{\sqrt {a}}}\psi \left({\frac {tb}{a}}\right),}$$

La proyección de una función x sobre el subespacio de escala a tiene entonces la forma con coeficientes wavelet$${\displaystyle x_{a}(t)=\int _{\mathbb {R} }WT_{\psi }\{x\}(a,b)\cdot \psi _{a,b}(t)\,db}$$$${\displaystyle WT_{\psi }\{x\}(a,b)=\langle x,\psi _{a,b}\rangle =\int _{\mathbb {R} }x(t){\psi _{a,b}(t)}\,dt.}$$

Para el análisis de la señal x , se pueden ensamblar los coeficientes wavelet en un escalagrama de la señal.

Vea una lista de algunas wavelets continuas .

Es computacionalmente imposible analizar una señal utilizando todos los coeficientes wavelet, por lo que uno puede preguntarse si es suficiente elegir un subconjunto discreto del semiplano superior para poder reconstruir una señal a partir de los coeficientes wavelet correspondientes. Uno de estos sistemas es el sistema afín para algunos parámetros reales a > 1, b > 0. El subconjunto discreto correspondiente del semiplano consiste en todos los puntos ( a ^m , nb a ^m ) con m , n en Z . Los wavelets secundarios correspondientes ahora se dan como$${\displaystyle \psi _{m,n}(t)={\frac {1}{\sqrt {a^{m}}}}\psi \left({\frac {t-nba^{m}}{a^{m}}}\right).}$$

Una condición suficiente para la reconstrucción de cualquier señal x de energía finita mediante la fórmula es que las funciones formen una base ortonormal de L ² ( R ).$${\displaystyle x(t)=\sum _{m\in \mathbb {Z} }\sum _{n\in \mathbb {Z} }\langle x,\,\psi _{m,n}\rangle \cdot \psi _{m,n}(t)}$$${\displaystyle \{\psi _{m,n}:m,n\in \mathbb {Z} \}}$

En cualquier transformada wavelet discretizada, solo hay un número finito de coeficientes wavelet para cada región rectangular acotada en el semiplano superior. Aún así, cada coeficiente requiere la evaluación de una integral. En situaciones especiales, esta complejidad numérica se puede evitar si los wavelets escalados y desplazados forman un análisis multirresolución . Esto significa que tiene que existir una función auxiliar , el wavelet padre φ en L ² ( R ), y que a es un entero. Una opción típica es a = 2 y b = 1. El par más famoso de wavelets padre y madre es el wavelet de 4 tomas de Daubechies . Nótese que no todas las bases wavelet discretas ortonormales se pueden asociar a un análisis multirresolución; por ejemplo, el wavelet de Journe no admite análisis multirresolución. ^[7]

A partir de las wavelets madre y padre se construyen los subespacios. La wavelet padre conserva las propiedades del dominio del tiempo, mientras que la wavelet madre conserva las propiedades del dominio de la frecuencia.$${\displaystyle V_{m}=\operatorname {span} (\phi _{m,n}:n\in \mathbb {Z} ),{\text{ where }}\phi _{m,n}(t)=2^{-m/2}\phi (2^{-m}t-n)}$$$${\displaystyle W_{m}=\operatorname {span} (\psi _{m,n}:n\in \mathbb {Z} ),{\text{ where }}\psi _{m,n}(t)=2^{-m/2}\psi (2^{-m}t-n).}$$${\displaystyle V_{i}}$${\displaystyle W_{i}}$

A partir de estos se requiere que la secuencia forme un análisis multirresolución de L ² y que los subespacios sean las "diferencias" ortogonales de la secuencia anterior, es decir, W _m es el complemento ortogonal de V _m dentro del subespacio V _{m −1} ,$${\displaystyle \{0\}\subset \dots \subset V_{1}\subset V_{0}\subset V_{-1}\subset V_{-2}\subset \dots \subset L^{2}(\mathbb {R} )}$$${\displaystyle \dots ,W_{1},W_{0},W_{-1},\dots }$$${\displaystyle V_{m}\oplus W_{m}=V_{m-1}.}$$

En analogía con el teorema de muestreo , se puede concluir que el espacio V _m con una distancia de muestreo de 2 ^m cubre más o menos la banda base de frecuencia de 0 a 1/2 ^{m -1} . Como complemento ortogonal, W _m cubre aproximadamente la banda [1/2 ^{m −1} , 1/2 ^m ].

De esas inclusiones y relaciones de ortogonalidad, especialmente , se sigue la existencia de sucesiones y que satisfacen las identidades de modo que y de modo que La segunda identidad del primer par es una ecuación de refinamiento para la wavelet padre φ. Ambos pares de identidades forman la base del algoritmo de la transformada wavelet rápida .${\displaystyle V_{0}\oplus W_{0}=V_{-1}}$${\displaystyle h=\{h_{n}\}_{n\in \mathbb {Z} }}$${\displaystyle g=\{g_{n}\}_{n\in \mathbb {Z} }}$$${\displaystyle g_{n}=\langle \phi _{0,0},\,\phi _{-1,n}\rangle }$$${\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}$$${\displaystyle h_{n}=\langle \psi _{0,0},\,\phi _{-1,n}\rangle }$$${\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}$

Del análisis multirresolución se deriva la descomposición ortogonal del espacio L ² como Para cualquier señal o función esto da una representación en funciones base de los subespacios correspondientes como donde los coeficientes son y$${\displaystyle L^{2}=V_{j_{0}}\oplus W_{j_{0}}\oplus W_{j_{0}-1}\oplus W_{j_{0}-2}\oplus W_{j_{0}-3}\oplus \cdots }$$${\displaystyle S\in L^{2}}$$${\displaystyle S=\sum _{k}c_{j_{0},k}\phi _{j_{0},k}+\sum _{j\leq j_{0}}\sum _{k}d_{j,k}\psi _{j,k}}$$$${\displaystyle c_{j_{0},k}=\langle S,\phi _{j_{0},k}\rangle }$$$${\displaystyle d_{j,k}=\langle S,\psi _{j,k}\rangle .}$$

Para procesar señales temporales en tiempo real, es esencial que los filtros wavelet no accedan a valores de señales del futuro y que se puedan obtener latencias temporales mínimas. Szu et al ^[8] y Lindeberg ^[9] desarrollaron representaciones wavelet causales en el tiempo ; este último método también implica una implementación recursiva en el tiempo que ahorra memoria.

Para aplicaciones prácticas, y por razones de eficiencia, se prefieren funciones continuamente diferenciables con soporte compacto como funciones wavelet madre (prototipo). Sin embargo, para satisfacer los requisitos analíticos (en la WT continua) y en general por razones teóricas, se eligen las funciones wavelet de un subespacio del espacio Este es el espacio de funciones medibles de Lebesgue que son a la vez absolutamente integrables e integrables al cuadrado en el sentido de que y${\displaystyle L^{1}(\mathbb {R} )\cap L^{2}(\mathbb {R} ).}$$${\displaystyle \int _{-\infty }^{\infty }|\psi (t)|\,dt<\infty }$$$${\displaystyle \int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt<\infty .}$$

Estar en este espacio asegura que uno pueda formular las condiciones de media cero y norma cuadrática uno: es la condición para media cero, y es la condición para norma cuadrática uno.$${\displaystyle \int _{-\infty }^{\infty }\psi (t)\,dt=0}$$$${\displaystyle \int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt=1}$$

Para que ψ sea una ondícula para la transformada ondícula continua (ver allí la declaración exacta), la ondícula madre debe satisfacer un criterio de admisibilidad (en términos generales, una especie de semidiferenciabilidad) para obtener una transformada establemente invertible.

Para la transformada wavelet discreta , se necesita al menos la condición de que la serie wavelet sea una representación de la identidad en el espacio L ² ( R ). La mayoría de las construcciones de WT discretas hacen uso del análisis multirresolución , que define la wavelet mediante una función de escala. Esta función de escala en sí misma es una solución a una ecuación funcional.

En la mayoría de las situaciones es útil restringir ψ para que sea una función continua con un número mayor M de momentos que se desvanecen, es decir, para todo entero m < M$${\displaystyle \int _{-\infty }^{\infty }t^{m}\,\psi (t)\,dt=0.}$$

La ondícula madre se escala (o dilata) por un factor de a y se traslada (o desplaza) por un factor de b para dar (según la formulación original de Morlet):

$${\displaystyle \psi _{a,b}(t)={1 \over {\sqrt {a}}}\psi \left({t-b \over a}\right).}$$

Para el WT continuo, el par ( a , b ) varía en todo el semiplano R ₊ × R ; para el WT discreto, este par varía en un subconjunto discreto del mismo, que también se denomina grupo afín .

A menudo se hace referencia incorrecta a estas funciones como funciones base de la transformada (continua). De hecho, al igual que en la transformada continua de Fourier, no existe base en la transformada continua de wavelets. La interpretación tiempo-frecuencia utiliza una formulación sutilmente diferente (según Delprat).

Restricción:

1. ${\displaystyle {\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt}$cuando a ₁ = a y b ₁ = b ,
2. ${\displaystyle \Psi (t)}$tiene un intervalo de tiempo finito

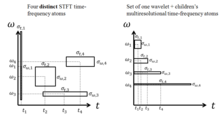
La transformada wavelet se compara a menudo con la transformada de Fourier , en la que las señales se representan como una suma de senos paranasales. De hecho, la transformada de Fourier puede considerarse un caso especial de la transformada wavelet continua con la elección de la wavelet madre . La principal diferencia en general es que las wavelets se localizan tanto en el tiempo como en la frecuencia, mientras que la transformada de Fourier estándar solo se localiza en la frecuencia . La transformada de Fourier de tiempo corto (STFT) es similar a la transformada wavelet, en el sentido de que también se localiza en el tiempo y la frecuencia, pero existen problemas con el equilibrio entre la resolución de frecuencia y tiempo.${\displaystyle \psi (t)=e^{-2\pi it}}$

En particular, suponiendo una región de ventana rectangular, se puede pensar en la STFT como una transformación con un núcleo ligeramente diferente donde a menudo se puede escribir como , donde y u denotan respectivamente la longitud y el desplazamiento temporal de la función de ventana. Utilizando el teorema de Parseval , se puede definir la energía de la wavelet como A partir de esto, el cuadrado del soporte temporal del desplazamiento de ventana por el tiempo u está dado por$${\displaystyle \psi (t)=g(t-u)e^{-2\pi it}}$$${\displaystyle g(t-u)}$${\textstyle \operatorname {rect} \left({\frac {t-u}{\Delta _{t}}}\right)}$${\displaystyle \Delta _{t}}$$${\displaystyle E=\int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt={\frac {1}{2\pi }}\int _{-\infty }^{\infty }|{\hat {\psi }}(\omega )|^{2}\,d\omega }$$$${\displaystyle \sigma _{u}^{2}={\frac {1}{E}}\int |t-u|^{2}|\psi (t)|^{2}\,dt}$$

y el cuadrado del soporte espectral de la ventana que actúa sobre una frecuencia${\displaystyle \xi }$$${\displaystyle {\hat {\sigma }}_{\xi }^{2}={\frac {1}{2\pi E}}\int |\omega -\xi |^{2}|{\hat {\psi }}(\omega )|^{2}\,d\omega }$$

La multiplicación con una ventana rectangular en el dominio del tiempo corresponde a la convolución con una función en el dominio de la frecuencia, lo que da como resultado artefactos de timbre espurios para ventanas temporales cortas/localizadas. Con la transformada de Fourier de tiempo continuo, y esta convolución es con una función delta en el espacio de Fourier, lo que da como resultado la transformada de Fourier verdadera de la señal . La función de ventana puede ser algún otro filtro apodizante , como un gaussiano . La elección de la función de ventana afectará el error de aproximación en relación con la transformada de Fourier verdadera.${\displaystyle \operatorname {sinc} (\Delta _{t}\omega )}$${\displaystyle \Delta _{t}\to \infty }$${\displaystyle x(t)}$

El producto de ancho de banda temporal de una celda de resolución dada no puede superarse con la STFT. Todos los elementos básicos de la STFT mantienen un soporte espectral y temporal uniforme para todos los desplazamientos o desfases temporales, logrando así una resolución temporal igual para frecuencias más altas y más bajas. La resolución está determinada exclusivamente por el ancho de muestreo.

Por el contrario, las propiedades multirresolucionales de la transformada wavelet permiten grandes soportes temporales para frecuencias más bajas, manteniendo al mismo tiempo anchos temporales cortos para frecuencias más altas gracias a las propiedades de escala de la transformada wavelet. Esta propiedad extiende el análisis convencional de tiempo-frecuencia al análisis de escala temporal. ^[10]

La transformada wavelet discreta es menos compleja computacionalmente , tomando O( N ) tiempo en comparación con O( N  log  N ) para la transformada rápida de Fourier (FFT). Esta ventaja computacional no es inherente a la transformada, sino que refleja la elección de una división logarítmica de frecuencia, en contraste con las divisiones de frecuencia igualmente espaciadas de la FFT que utiliza las mismas funciones base que la transformada discreta de Fourier (DFT). ^[11] Esta complejidad solo se aplica cuando el tamaño del filtro no tiene relación con el tamaño de la señal. Una wavelet sin soporte compacto como la wavelet de Shannon requeriría O( N ² ). (Por ejemplo, una transformada de Fourier logarítmica también existe con complejidad O( N ), pero la señal original debe muestrearse logarítmicamente en el tiempo, lo que solo es útil para ciertos tipos de señales. ^[12] )

Una wavelet (o una familia de wavelets) se puede definir de varias maneras:

Una wavelet ortogonal está completamente definida por el filtro de escala: un filtro de respuesta de impulso finito (FIR) de paso bajo de longitud 2 N y suma 1. En las wavelets biortogonales , se definen filtros de descomposición y reconstrucción separados.

Para el análisis con wavelets ortogonales, el filtro de paso alto se calcula como el filtro de espejo en cuadratura del filtro de paso bajo, y los filtros de reconstrucción son el inverso temporal de los filtros de descomposición.

Las wavelets Daubechies y Symlet se pueden definir mediante el filtro de escala.

Las wavelets se definen mediante la función wavelet ψ( t ) (es decir, la wavelet madre) y la función de escala φ( t ) (también llamada wavelet padre) en el dominio del tiempo.

La función wavelet es en efecto un filtro de paso de banda y su escalamiento para cada nivel reduce a la mitad su ancho de banda. Esto crea el problema de que para cubrir todo el espectro, se necesitaría una cantidad infinita de niveles. La función de escalamiento filtra el nivel más bajo de la transformación y garantiza que se cubra todo el espectro. Consulte ^[13] para obtener una explicación detallada.

Para una ondícula con soporte compacto, φ( t ) puede considerarse finito en longitud y es equivalente al filtro de escala g .

Las wavelets de Meyer se pueden definir mediante funciones de escala

La ondícula solo tiene una representación en el dominio del tiempo como la función ondícula ψ( t ).

Por ejemplo, las ondículas de un sombrero mexicano se pueden definir mediante una función ondícula. Vea una lista de algunas ondículas continuas .

El desarrollo de las wavelets puede vincularse a varias líneas de pensamiento independientes, comenzando con el trabajo de Alfréd Haar a principios del siglo XX. El trabajo posterior de Dennis Gabor produjo los átomos de Gabor (1946), que están construidos de manera similar a las wavelets y se aplican a fines similares.

Las contribuciones notables a la teoría de wavelets desde entonces se pueden atribuir al descubrimiento de George Zweig de la transformada wavelet continua (CWT) en 1975 (originalmente llamada transformada coclear y descubierta mientras estudiaba la reacción del oído al sonido), ^[14] la formulación de Pierre Goupillaud, Alex Grossmann y Jean Morlet de lo que ahora se conoce como CWT (1982), el trabajo temprano de Jan-Olov Strömberg sobre wavelets discretos (1983), el banco de filtros no ortogonales de 5/3 tomas Le Gall-Tabatabai (LGT) con fase lineal (1988), ^{[15] [16] [17]} las wavelets ortogonales con soporte compacto de Ingrid Daubechies (1988), el marco multirresolución no ortogonal de Stéphane Mallat (1989), el QMF binomial de Ali Akansu (1990), la interpretación tiempo-frecuencia de Nathalie Delprat CWT (1991), transformada wavelet armónica de Newland (1993) y partición de conjuntos en árboles jerárquicos (SPIHT) desarrollada por Amir Said con William A. Pearlman en 1996. ^[18]

El estándar JPEG 2000 fue desarrollado entre 1997 y 2000 por un comité del Joint Photographic Experts Group (JPEG) presidido por Touradj Ebrahimi (posteriormente presidente del JPEG). ^[19] A diferencia del algoritmo DCT utilizado por el formato JPEG original , JPEG 2000 utiliza algoritmos de transformada wavelet discreta (DWT). Utiliza la transformada wavelet CDF 9/7 (desarrollada por Ingrid Daubechies en 1992) para su algoritmo de compresión con pérdida , y el banco de filtros de tiempo discreto Le Gall–Tabatabai (LGT) 5/3 (desarrollado por Didier Le Gall y Ali J. Tabatabai en 1988) para su algoritmo de compresión sin pérdida . ^{[20] La tecnología} JPEG 2000 , que incluye la extensión Motion JPEG 2000 , fue seleccionada como el estándar de codificación de vídeo para el cine digital en 2004. ^[21]

• Primera wavelet ( wavelet de Haar ) de Alfréd Haar (1909)
• Desde los años 1970: George Zweig , Jean Morlet , Alex Grossmann
• Desde los años 1980: Yves Meyer , Didier Le Gall, Ali J. Tabatabai, Stéphane Mallat , Ingrid Daubechies , Ronald Coifman , Ali Akansu , Victor Wickerhauser
• Desde los años 1990: Nathalie Delprat, Newland, Amir Said, William A. Pearlman, Touradj Ebrahimi, JPEG 2000

Una wavelet es una función matemática que se utiliza para dividir una función dada o una señal de tiempo continuo en diferentes componentes de escala. Por lo general, se puede asignar un rango de frecuencia a cada componente de escala. Luego, cada componente de escala se puede estudiar con una resolución que coincida con su escala. Una transformada wavelet es la representación de una función mediante wavelets. Los wavelets son copias escaladas y trasladadas (conocidas como "wavelets hijas") de una forma de onda oscilante de longitud finita o de decaimiento rápido (conocida como "wavelet madre"). Las transformadas wavelet tienen ventajas sobre las transformadas de Fourier tradicionales para representar funciones que tienen discontinuidades y picos agudos, y para deconstruir y reconstruir con precisión señales finitas, no periódicas y/o no estacionarias .

Las transformadas wavelet se clasifican en transformadas wavelet discretas (DWT) y transformadas wavelet continuas (CWT). Tenga en cuenta que tanto las DWT como las CWT son transformadas de tiempo continuo (analógicas). Se pueden utilizar para representar señales de tiempo continuo (analógicas). Las CWT operan sobre todas las posibles escalas y traducciones, mientras que las DWT utilizan un subconjunto específico de valores de escala y traducción o una cuadrícula de representación.

Existe una gran cantidad de transformadas wavelet, cada una de ellas adecuada para diferentes aplicaciones. Para obtener una lista completa, consulte la lista de transformadas relacionadas con wavelet, pero las más comunes se enumeran a continuación:

• Transformada wavelet continua (CWT)
• Transformada wavelet discreta (DWT)
• Transformada wavelet rápida (FWT)
• Esquema de elevación y esquema de elevación generalizado
• Descomposición de paquetes wavelet (WPD)
• Transformada wavelet estacionaria (SWT)
• Transformada de Fourier Fraccionaria (FRFT)
• Transformada wavelet fraccional (FRWT)

Hay varias transformadas generalizadas de las cuales la transformada wavelet es un caso especial. Por ejemplo, Yosef Joseph Segman introdujo la escala en el grupo de Heisenberg , lo que dio lugar a un espacio de transformada continua que es una función del tiempo, la escala y la frecuencia. La CWT es un corte bidimensional a través del volumen de escala de tiempo-frecuencia tridimensional resultante.

Otro ejemplo de una transformación generalizada es la transformación chirplet en la que la CWT también es un corte bidimensional a través de la transformación chirplet.

Un área de aplicación importante para las transformadas generalizadas involucra sistemas en los que la resolución de alta frecuencia es crucial. Por ejemplo, las transformadas ópticas electrónicas de campo oscuro intermedias entre el espacio directo y recíproco se han utilizado ampliamente en el análisis armónico de agrupamiento de átomos, es decir, en el estudio de cristales y defectos cristalinos . ^[22] Ahora que los microscopios electrónicos de transmisión son capaces de proporcionar imágenes digitales con información a escala picométrica sobre la periodicidad atómica en nanoestructuras de todo tipo, el rango de aplicaciones de reconocimiento de patrones ^[23] y deformación ^[24] / metrología ^[25] para transformadas intermedias con resolución de alta frecuencia (como brushlets ^[26] y ridgelets ^[27] ) está creciendo rápidamente.

La transformada wavelet fraccional (FRWT) es una generalización de la transformada wavelet clásica en los dominios de la transformada de Fourier fraccional. Esta transformada es capaz de proporcionar la información del dominio temporal y fraccional simultáneamente y representar señales en el plano temporal-fraccional-frecuencia. ^[28]

Generalmente, se utiliza una aproximación a DWT para la compresión de datos si ya se muestreó una señal, y la CWT para el análisis de señales . ^{[29] [30]} Por lo tanto, la aproximación DWT se utiliza comúnmente en ingeniería y ciencias de la computación, ^[31] y la CWT en investigación científica. ^[32]

Al igual que otras transformaciones, las transformadas wavelet se pueden utilizar para transformar datos y luego codificar los datos transformados, lo que da como resultado una compresión efectiva. Por ejemplo, JPEG 2000 es un estándar de compresión de imágenes que utiliza wavelets biortogonales. Esto significa que, aunque el cuadro es sobrecompleto, es un cuadro ajustado (consulte tipos de cuadros de un espacio vectorial ), y se utilizan las mismas funciones de cuadro (excepto la conjugación en el caso de wavelets complejos) tanto para el análisis como para la síntesis, es decir, tanto en la transformación directa como en la inversa. Para obtener más detalles, consulte compresión wavelet .

Un uso relacionado es el de suavizar o eliminar el ruido de los datos en función del umbral de coeficientes de ondículas, también denominado contracción de ondículas. Mediante la umbralización adaptativa de los coeficientes de ondículas que corresponden a componentes de frecuencia no deseados, se pueden realizar operaciones de suavizado o eliminación de ruido.

Las transformadas wavelet también están empezando a utilizarse para aplicaciones de comunicación. Wavelet OFDM es el esquema de modulación básico utilizado en HD-PLC (una tecnología de comunicaciones por línea eléctrica desarrollada por Panasonic ), y en uno de los modos opcionales incluidos en el estándar IEEE 1901. Wavelet OFDM puede lograr cortes más profundos que la FFT OFDM tradicional, y wavelet OFDM no requiere un intervalo de guarda (que normalmente representa una sobrecarga significativa en los sistemas FFT OFDM). ^[33]

A menudo, las señales se pueden representar bien como una suma de senos. Sin embargo, considere una señal no continua con una discontinuidad abrupta; esta señal aún se puede representar como una suma de senos, pero requiere un número infinito, que es una observación conocida como fenómeno de Gibbs . Esto, entonces, requiere un número infinito de coeficientes de Fourier, lo que no es práctico para muchas aplicaciones, como la compresión. Las wavelets son más útiles para describir estas señales con discontinuidades debido a su comportamiento localizado en el tiempo (tanto las transformadas de Fourier como las de wavelets están localizadas en la frecuencia, pero las wavelets tienen una propiedad adicional de localización en el tiempo). Debido a esto, muchos tipos de señales en la práctica pueden no ser dispersas en el dominio de Fourier, pero muy dispersas en el dominio de wavelets. Esto es particularmente útil en la reconstrucción de señales, especialmente en el campo recientemente popular de la detección comprimida . (Tenga en cuenta que la transformada de Fourier de tiempo corto (STFT) también está localizada en el tiempo y la frecuencia, pero a menudo hay problemas con el equilibrio entre la resolución de frecuencia y tiempo. Las wavelets son mejores representaciones de señales debido al análisis de múltiples resoluciones ).

Esto motiva por qué las transformadas wavelet ahora se están adoptando para una gran cantidad de aplicaciones, a menudo reemplazando la transformada de Fourier convencional . Muchas áreas de la física han visto este cambio de paradigma, incluyendo la dinámica molecular , la teoría del caos , ^{[34] los cálculos} ab initio , la astrofísica , el análisis de datos transitorios de ondas gravitacionales , ^{[35] [36]} la localización de la matriz de densidad , la sismología , la óptica , la turbulencia y la mecánica cuántica . Este cambio también ha ocurrido en el procesamiento de imágenes , EEG , EMG , ^[37] análisis de ECG , ritmos cerebrales , análisis de ADN , análisis de proteínas , climatología , análisis de la respuesta sexual humana, ^[38] procesamiento general de señales , reconocimiento de voz , acústica, señales de vibración, ^[39] gráficos de computadora , análisis multifractal y codificación dispersa . En la visión por computadora y el procesamiento de imágenes , la noción de representación del espacio de escala y los operadores derivados gaussianos se consideran una representación multiescala canónica.

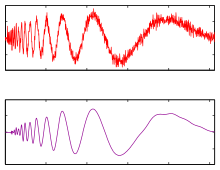
Supongamos que medimos una señal ruidosa , donde representa la señal y representa el ruido. Supongamos que tiene una representación dispersa en una base de ondículas determinada, y${\displaystyle x=s+v}$${\displaystyle s}$${\displaystyle v}$${\displaystyle s}$${\displaystyle v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)}$

Sea la transformada wavelet de , donde es la transformada wavelet del componente de señal y es la transformada wavelet del componente de ruido.${\displaystyle x}$${\displaystyle y=W^{T}x=W^{T}s+W^{T}v=p+z}$${\displaystyle p=W^{T}s}$${\displaystyle z=W^{T}v}$

La mayoría de los elementos son 0 o cercanos a 0, y${\displaystyle p}$${\displaystyle z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)}$

Como es ortogonal, el problema de estimación consiste en recuperar una señal en un ruido gaussiano iid . Como es escaso, un método consiste en aplicar un modelo de mezcla gaussiana para .${\displaystyle W}$${\displaystyle p}$${\displaystyle p}$

Supongamos una anterior , donde es la varianza de los coeficientes "significativos" y es la varianza de los coeficientes "insignificantes".${\displaystyle p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})}$${\displaystyle \sigma _{1}^{2}}$${\displaystyle \sigma _{2}^{2}}$

Entonces , se llama factor de contracción, que depende de las varianzas anteriores y . Al establecer coeficientes que caen por debajo de un umbral de contracción a cero, una vez que se aplica la transformada inversa, se pierde una cantidad esperada pequeña de señal debido al supuesto de escasez. Se espera que los coeficientes más grandes representen principalmente la señal debido a la escasez, y estadísticamente se espera que muy poco de la señal, aunque la mayoría del ruido, esté representado en coeficientes de magnitud tan bajos... por lo tanto, se espera que la operación de puesta a cero elimine la mayor parte del ruido y no mucha señal. Normalmente, los coeficientes por encima del umbral no se modifican durante este proceso. Algunos algoritmos para la eliminación de ruido basada en ondículas también pueden atenuar coeficientes más grandes, según una estimación estadística de la cantidad de ruido que se espera eliminar con dicha atenuación.${\displaystyle {\tilde {p}}=E(p/y)=\tau (y)y}$${\displaystyle \tau (y)}$${\displaystyle \sigma _{1}^{2}}$${\displaystyle \sigma _{2}^{2}}$

Por último, aplique la transformada wavelet inversa para obtener${\displaystyle {\tilde {s}}=W{\tilde {p}}}$

Agarwal et al. propusieron métodos lineales avanzados basados ​​en ondículas ^[40] y no lineales ^{[41] para construir e investigar} el clima como redes complejas en diferentes escalas de tiempo. Las redes climáticas construidas utilizando conjuntos de datos de SST en diferentes escalas de tiempo afirmaron que el análisis multiescala basado en ondículas de los procesos climáticos promete una mejor comprensión de la dinámica del sistema que puede pasarse por alto cuando los procesos se analizan en una sola escala de tiempo ^[42].

• Beylkín (18)
• Ondícula de Moore Ondícula de Morlet
• Ondículas biortogonales casi coiflet (BNC)
• Coiflet (6, 12, 18, 24, 30)
• Ondícula de Cohen-Daubechies-Feauveau (a veces denominada CDF N/P o ondícula biortogonal de Daubechies)
• Ondícula de Daubechies (2, 4, 6, 8, 10, 12, 14, 16, 18, 20, etc.)
• QMF binomial (también conocida como wavelet de Daubechies)
• Ondícula de Haar
• Ondícula de Mathieu
• Ondícula de Legendre
• Ondeleta de Villaseñor
• Símbolo ^[43]

• Ondícula beta
• Ondícula hermítica
• Ondícula Meyer
• Ondulación de sombrero mexicano
• Ondícula de Poisson
• Ondícula de Shannon
• Ondícula spline
• Ondícula de Strömberg

• Ondícula compleja de sombrero mexicano
• ondícula fbsp
• Ondícula de Morlet
• Ondícula de Shannon
• Ondícula de Morlet modificada

• Transformación de Chirplet
• Curva
• Cine digital
• Reducción de dimensión
• Bancos de filtros
• Transformadas relacionadas con Fourier
• Compresión fractal
• Transformada de Fourier fraccionaria
• Wavelet de Gabor § Espacio wavelet ^[44]
• Principio de Huygens-Fresnel (ondículas físicas)
• JPEG2000
• Análisis espectral de mínimos cuadrados para calcular la periodicidad en cualquier dato, incluidos los datos espaciados de manera desigual
• Ondícula de Morlet
• Análisis multiresolución
• Ruido
• Ondícula no separable
• Espacio de escala
• Correlación escalada
• Shearlet
• Transformada de Fourier de corta duración
• Espectrograma
• Radio de banda ultra ancha : transmite ondas pequeñas

• Haar A., ​​Zur Theorie der orthogonalen Funktionensysteme , Mathematische Annalen, 69 , págs. 331–371, 1910.
• Ingrid Daubechies , Diez conferencias sobre wavelets , Sociedad de Matemáticas Industriales y Aplicadas, 1992, ISBN 0-89871-274-2 . 
• Ali Akansu y Richard Haddad, Descomposición de señales multiresolución: transformadas, subbandas, wavelets , Academic Press, 1992, ISBN 0-12-047140-X . 
• PP Vaidyanathan , Sistemas multifrecuencia y bancos de filtros , Prentice Hall, 1993, ISBN 0-13-605718-7 . 
• Gerald Kaiser, Una guía amigable para wavelets , Birkhauser, 1994, ISBN 0-8176-3711-7 . 
• Mladen Victor Wickerhauser, Análisis wavelet adaptado de la teoría al software , AK Peters Ltd, 1994, ISBN 1-56881-041-5 . 
• Martin Vetterli y Jelena Kovačević, "Wavelets y codificación de subbandas", Prentice Hall, 1995, ISBN 0-13-097080-8 . 
• Barbara Burke Hubbard , "El mundo según las wavelets: La historia de una técnica matemática en desarrollo", AK Peters Ltd, 1998, ISBN 1-56881-072-5 , ISBN 978-1-56881-072-0 .  
• Stéphane Mallat , "Un recorrido wavelet por el procesamiento de señales", 2ª edición, Academic Press, 1999, ISBN 0-12-466606-X . 
• Donald B. Percival y Andrew T. Walden, Métodos wavelet para análisis de series de tiempo , Cambridge University Press, 2000, ISBN 0-521-68508-7 . 
• Ramazan Gençay, Faruk Selçuk y Brandon Whitcher, Introducción a wavelets y otros métodos de filtrado en finanzas y economía , Academic Press, 2001, ISBN 0-12-279670-5 . 
• Paul S. Addison, The Illustrated Wavelet Transform Handbook , Instituto de Física , 2002, ISBN 0-7503-0692-0 . 
• B. Boashash, editor, "Análisis y procesamiento de señales de tiempo-frecuencia: una referencia completa", Elsevier Science, Oxford, 2003, ISBN 0-08-044335-4 . 
• Tony F. Chan y Jackie (Jianhong) Shen, Procesamiento y análisis de imágenes: métodos variacionales, PDE, wavelet y estocásticos , Society of Applied Mathematics, ISBN 0-89871-589-X (2005). 
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Sección 13.10. Transformadas wavelet", Recetas numéricas: el arte de la computación científica (3.ª ed.), Nueva York: Cambridge University Press, ISBN 978-0-85-0-312-0 978-0-521-88068-8, archivado desde el original el 11-08-2011 , consultado el 13-08-2011.
• "Cómo los wavelets permiten a los investigadores transformar y comprender los datos". Quanta Magazine . 2021-10-13 . Consultado el 2021-10-20 .

This section's use of external links may not follow Wikipedia's policies or guidelines. Please improve this article by removing excessive or inappropriate external links, and converting useful links where appropriate into footnote references. (July 2016) (Learn how and when to remove this message)

Busque wavelet en Wikcionario, el diccionario libre.

Wikimedia Commons tiene medios relacionados con Wavelet.

Wikiquote tiene citas relacionadas con Wavelet .

• "Análisis wavelet", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• 1er Simposio NJIT sobre Wavelets (30 de abril de 1990) (Primera Conferencia sobre Wavelets en EE.UU.)
• Wavelets de Daubechies de QMF binomial
• Wavelets, de Gilbert Strang, American Scientist 82 (1994), pp. 250-255. (Una introducción muy breve y excelente)
• Curso sobre Wavelets impartido en la Universidad de California en Santa Bárbara, 2004
• Wavelets para niños (archivo PDF) (Introducción (¡para niños muy inteligentes!))
• WITS: ¿Dónde está la estrella? Un diccionario de decenas de wavelets y términos relacionados con wavelets que terminan en -let, desde activelets hasta x-lets, pasando por bandlets, contourlets, curvelets, noiselets y wedgelets.
• La transformada wavelet de spline fraccional describe una transformada wavelet fraccional basada en b-Splines fraccionales.
• Un panorama sobre representaciones geométricas multiescala, entrelazando selectividad espacial, direccional y de frecuencia proporciona un tutorial sobre wavelets orientados bidimensionales y transformaciones geométricas multiescala relacionadas.
• Breve introducción a las wavelets de René Puschinger
• Una guía muy sencilla sobre wavelets, de Clemens Valens
• "Cómo los wavelets permiten a los investigadores transformar y comprender los datos". Quanta Magazine . 2021-10-13 . Consultado el 2021-10-20 .