Historia del sistema métrico

La historia del sistema métrico comienza durante la época de las Luces, con medidas de longitud y peso derivadas de la naturaleza , junto con sus múltiplos decimales y fracciones. El sistema se convirtió en el estándar de Francia y Europa en menos de medio siglo. Se añadieron otras medidas con proporciones unitarias ^{[Nota 1]} y el sistema pasó a ser adoptado en todo el mundo.

La primera realización práctica del sistema métrico se produjo en 1799, durante la Revolución Francesa , después de que el sistema de medidas existente se había vuelto impráctico para el comercio y fue reemplazado por un sistema decimal basado en el kilogramo y el metro . Las unidades básicas se tomaron del mundo natural. La unidad de longitud, el metro, se basó en las dimensiones de la Tierra , y la unidad de masa , el kilogramo, se basó en la masa de un volumen de agua de un litro (un decímetro cúbico ). Se fabricaron copias de referencia para ambas unidades en platino y siguieron siendo los estándares de medida durante los siguientes 90 años. Después de un período de vuelta a las medidas usuales debido a la impopularidad del sistema métrico, la metrificación de Francia y gran parte de Europa se completó en la década de 1850.

A mediados del siglo XIX, James Clerk Maxwell concibió un sistema coherente en el que se definían un pequeño número de unidades de medida como unidades base , y todas las demás unidades de medida, llamadas unidades derivadas , se definían en términos de las unidades base. Maxwell propuso tres unidades base para la longitud, la masa y el tiempo. Los avances en electromagnetismo en el siglo XIX requirieron la definición de unidades adicionales, y comenzaron a usarse múltiples sistemas incompatibles de tales unidades; ninguno podía reconciliarse con el sistema dimensional existente. El impasse fue resuelto por Giovanni Giorgi , quien en 1901 demostró que un sistema coherente que incorporara unidades electromagnéticas requería una cuarta unidad base, la del electromagnetismo.

El influyente Tratado del Metro de 1875 dio lugar a la creación y distribución de artefactos de metros y kilogramos, los estándares del futuro sistema coherente que se convirtió en el SI, y a la creación de un organismo internacional, la Conferencia General de Pesos y Medidas o CGPM, para supervisar los sistemas de pesos y medidas basados ​​en ellos.

En 1960, la CGPM lanzó el Sistema Internacional de Unidades (en francés Système international d'unités o SI) con seis "unidades básicas": el metro, el kilogramo, el segundo , el amperio , el grado Kelvin (posteriormente rebautizado como "kelvin") y la candela , además de 16 unidades más derivadas de las unidades básicas. Una séptima unidad básica, el mol , y otras seis unidades derivadas se añadieron más tarde en el siglo XX. Durante este período, el metro se redefinió en términos de la velocidad de la luz, y el segundo se redefinió basándose en la frecuencia de microondas de un reloj atómico de cesio .

Debido a la inestabilidad del prototipo internacional del kilogramo , se emprendieron una serie de iniciativas, a partir de fines del siglo XX, para redefinir el amperio, el kilogramo, el mol y el kelvin en términos de constantes invariantes de la física , lo que finalmente resultó en la revisión de 2019 del SI , que finalmente eliminó la necesidad de cualquier artefacto de referencia física; en particular, esto permitió el retiro del kilogramo estándar.

Se puede encontrar un indicio fugaz de un antiguo sistema decimal o métrico en la regla de Mohenjo-Daro , que utiliza una longitud de base de 1,32 pulgadas (33,5 mm) y está dividida con gran precisión mediante marcas decimales. Los ladrillos de ese período son consistentes con esta unidad, pero este uso parece no haber sobrevivido, ya que los sistemas posteriores en la India no son métricos y emplean divisiones en octavos, doceavos y dieciseisavos.

Los aspectos fundamentales de las matemáticas, junto con una mayor comprensión del mundo natural durante la Ilustración, prepararon el terreno para el surgimiento, a finales del siglo XVIII, de un sistema de medición con unidades racionalmente relacionadas y reglas para combinarlas.

A principios del siglo IX, cuando gran parte de lo que luego se convertiría en el Sacro Imperio Romano Germánico formaba parte de Francia, el emperador Carlomagno había estandarizado las unidades de medida . Había introducido unidades de medida estándar para la longitud y la masa en todo su imperio. A medida que el imperio se desintegraba en naciones separadas, incluida Francia, estos estándares divergieron. En Inglaterra, la Carta Magna (1215) había estipulado que "Habrá medidas estándar para el vino, la cerveza y el trigo (el cuarto de Londres) en todo el reino. También habrá un ancho estándar para las telas teñidas, rojizas y de mercería, es decir, dos codos dentro de los orillos. Los pesos se estandarizarán de manera similar". ^[1]

Durante la época medieval temprana , los números romanos se usaban en Europa para representar números, ^[2] pero los árabes representaban los números usando el sistema de numeración hindú , una notación posicional que usaba diez símbolos. Alrededor de 1202, Fibonacci publicó su libro Liber Abaci (Libro de cálculo) que introdujo el concepto de notación posicional en Europa. Estos símbolos evolucionaron en los numerales "0", "1", "2", etc. ^{[3] [4]} En ese momento, había una disputa con respecto a la diferencia entre números racionales y números irracionales y no había consistencia en la forma en que se representaban las fracciones decimales.

A Simon Stevin se le atribuye la introducción del sistema decimal en Europa. ^[5] En 1586, publicó un pequeño panfleto llamado De Thiende ("el décimo") que los historiadores consideran la base de la notación moderna para las fracciones decimales. ^[6] Stevin consideró que esta innovación era tan significativa que declaró que la introducción universal de monedas, medidas y pesos decimales era simplemente una cuestión de tiempo. ^{[5] [7] : 70  [8] : 91}

Desde la época de Carlomagno, el estandarte de longitud había sido una medida del cuerpo, la de la punta de un dedo a la punta de los brazos extendidos de un hombre grande, ^{[Nota 2]} de una familia de medidas corporales llamadas brazas , originalmente utilizadas, entre otras cosas, para medir la profundidad del agua. Un artefacto para representar el estandarte se fundió en el material más duradero disponible en la Edad Media, una barra de hierro ^{[ cita requerida ]} . Los problemas de un artefacto no reproducible se hicieron evidentes con el paso de los siglos: se oxidaba, era robado, golpeado contra una pared hundida hasta que se doblaba y, a veces, se perdía. Cuando había que fundir un nuevo estandarte real, era un estandarte diferente al antiguo, por lo que surgieron y se utilizaron réplicas de los antiguos y de los nuevos. El artefacto existió hasta el siglo XVIII y se llamó teise o, más tarde, toise (del latín tense : extendido (brazos)). Esto conduciría a una búsqueda en el siglo XVIII de un estándar reproducible basado en alguna medida invariable del mundo natural.

En 1656, el científico holandés Christiaan Huygens inventó el reloj de péndulo, cuyo péndulo marcaba los segundos. Esto dio lugar a propuestas para utilizar su longitud como unidad estándar. Pero se hizo evidente que las longitudes de los péndulo de los relojes calibrados en diferentes lugares variaban (debido a las variaciones locales en la aceleración debida a la gravedad ), y esta no era una buena solución. Se necesitaba un estándar más uniforme.

En 1670, Gabriel Mouton , abad y astrónomo francés, publicó el libro Observationes diametrorum solis et lunae aspectium ("Observaciones de los diámetros aparentes del Sol y la Luna") en el que proponía un sistema decimal de medición de longitud para uso de los científicos en la comunicación internacional, que se basaría en las dimensiones de la Tierra. El miliárea se definiría como un minuto de arco a lo largo de un meridiano (como el meridiano de París ) y se dividiría en 10 centurias, la centuria en 10 decurias y así sucesivamente, siendo las unidades sucesivas la virga, la vírgula, la décima, la centésima y la milésima. Mouton utilizó la estimación de Riccioli de que un grado de arco eran 321.185 pies boloñeses. Los experimentos de Mouton mostraron que un péndulo de una vírgula de longitud latía 3959,2 veces ^{[Nota 3]} en media hora. ^{[9] [Nota 4]} Mouton creía que, con esta información, los científicos de un país extranjero podrían construir una copia de la vírgula para su propio uso. ^[10] Las ideas de Mouton atrajeron interés en ese momento; Picard en su obra Mesure de la Terre (1671) y Huygens en su obra Horologium Oscillatorium sive de motu pendulorum ("De los relojes oscilantes, o sobre el movimiento de los péndulos", 1673) propusieron que una unidad estándar de longitud se vinculara a la frecuencia de batido de un péndulo. ^{[11] [10]}

Desde al menos la Edad Media, la Tierra había sido percibida como eterna, inmutable y de forma simétrica (cercana a una esfera), por lo que era natural que se propusiera alguna medida fraccionaria de su superficie como estándar de longitud. Pero primero, se debía obtener información científica sobre la forma y el tamaño de la Tierra. Un grado de arco sería 60 minutos de arco, en el ecuador; un miliárea sería un minuto de arco, o 1 milla náutica, por lo que 60 millas náuticas serían un grado de arco en la superficie de la Tierra, tomada como una esfera . ^[12] Por lo tanto, la circunferencia de la Tierra en millas náuticas sería 21 600 (es decir, 60 minutos de arco × 360 grados en cuatro cuadrantes de 90 grados; un cuadrante es la longitud del cuarto de círculo desde el Polo Norte hasta el ecuador ).

En 1669, Jean Picard , un astrónomo francés, fue la primera persona en medir la Tierra con precisión. En un estudio que abarcó un grado de latitud, se equivocó solo en un 0,44 % ( medición del arco de Picard ).

En Philosophiæ Naturalis Principia Mathematica (1686), Isaac Newton dio una explicación teórica para el "ecuador abultado", ^{[Nota 5]} que también explicaba las diferencias encontradas en las longitudes de los "segundos péndulos", ^[13] teorías que fueron confirmadas por la Misión Geodésica Francesa al Perú realizada por la Academia Francesa de Ciencias en 1735. ^{[14] [a]}

A mediados del siglo XVIII, se hizo evidente que era necesario estandarizar los pesos y medidas entre las naciones que comerciaban e intercambiaban ideas científicas entre sí. España, por ejemplo, había alineado sus unidades de medida con las unidades reales de Francia ^[17] y Pedro el Grande alineó las unidades de medida rusas con las de Inglaterra. ^[18] En 1783, el inventor británico James Watt , que tenía dificultades para comunicarse con los científicos alemanes, pidió la creación de un sistema de medición decimal global, proponiendo un sistema que utilizara la densidad del agua para vincular la longitud y la masa, ^[16] y, en 1788, el químico francés Antoine Lavoisier encargó un conjunto de nueve cilindros de latón (una libra [francesa] y subdivisiones decimales de la misma) para su trabajo experimental. ^{[7] : 71}

En 1790, una propuesta lanzada por los franceses a Gran Bretaña y los Estados Unidos para establecer una medida uniforme de longitud, un metro basado en el período de un péndulo con un latido de un segundo, fue derrotada en el Parlamento británico y el Congreso de los Estados Unidos. El problema subyacente fue la falta de acuerdo sobre la latitud para la definición, ya que la aceleración gravitacional y, por lo tanto, la longitud del péndulo, varía (entre otras cosas) con la latitud: cada parte quería una definición según una latitud principal que pasara por su propio país. Las consecuencias directas del fracaso fueron el desarrollo y despliegue unilateral francés del sistema métrico y su difusión a través del comercio al continente; la adopción británica del Sistema Imperial de Medidas en todo el reino en 1824; y la retención por parte de los Estados Unidos del sistema común británico de medidas vigente en el momento de la independencia de las colonias. Esta fue la posición que se mantuvo durante casi los siguientes 200 años. ^{[Nota 6]}

Se ha estimado que, en vísperas de la Revolución de 1789, las aproximadamente ochocientas unidades de medida en uso en Francia tenían hasta un cuarto de millón de definiciones diferentes porque la cantidad asociada con cada unidad podía diferir de una ciudad a otra, e incluso de un comercio a otro. ^{[8] : 2–3} Aunque ciertos estándares, como el pied du roi (el pie del rey) tenían un grado de preeminencia y eran utilizados por científicos, muchos comerciantes optaron por utilizar sus propios dispositivos de medición, lo que dio lugar al fraude y obstaculizó el comercio y la industria. ^[19] Estas variaciones fueron promovidas por intereses creados locales, pero obstaculizaron el comercio y los impuestos. ^{[20] [21]}

En 1790, la Academia de Ciencias designó a un grupo de cinco científicos franceses destacados para que investigaran los pesos y las medidas. Eran Jean-Charles de Borda , Joseph-Louis Lagrange , Pierre-Simon Laplace , Gaspard Monge y Nicolas de Condorcet . ^{[8] : 2–3  [22] : 46} Durante el año siguiente, el grupo, después de estudiar varias alternativas, hizo una serie de recomendaciones con respecto a un nuevo sistema de pesos y medidas, incluyendo que debería tener un radix decimal , que la unidad de longitud debería basarse en un arco fraccionario de un cuadrante del meridiano de la Tierra, y que la unidad de peso debería ser la de un cubo de agua cuya dimensión fuera una fracción decimal de la unidad de longitud. ^{[23] [24] [7] : 50–51  [25] [26]} Las propuestas fueron aceptadas por la Asamblea Francesa el 30 de marzo de 1791. ^[27]

Tras la aceptación, se encargó a la Academia de Ciencias que aplicara las propuestas. La Academia dividió las tareas en cinco operaciones y asignó cada parte a un grupo de trabajo independiente : ^{[7] : 82}

• Medición de la diferencia de latitud entre Dunkerque y Barcelona y triangulación entre ellas
• Medición de las líneas de base utilizadas para la encuesta
• Verificación de la longitud del segundo péndulo a 45° de latitud.
• Verificación del peso en el vacío de un volumen dado de agua destilada.
• Publicar tablas de conversión relacionando las nuevas unidades de medida con las unidades de medida existentes.

El panel decidió que la nueva medida de longitud debería ser igual a una diezmillonésima parte de la distancia desde el Polo Norte hasta el Ecuador ( cuadrante terrestre ), medida a lo largo del meridiano de París . ^[20]

Utilizando el estudio de Jean Picard de 1670 y el de Jacques Cassini de 1718, ^[a] se asignó al metro un valor provisional de 443,44 líneas ^{que, a su vez, definía las otras unidades de medida. [8] : 106}

Mientras Méchain y Delambre terminaban su trabajo, la comisión había ordenado que se fabricaran una serie de lingotes de platino basados ​​en el metro provisional. Cuando se conociera el resultado definitivo, se seleccionaría el lingote cuya longitud se aproximara más a la definición meridional del metro.

Después de 1792, se adoptó el nombre de la unidad de masa definida originalmente, " gramo ", que era demasiado pequeña para servir como una realización práctica para muchos propósitos, y se le agregó el nuevo prefijo "kilo" para formar el nombre " kilogramo ". En consecuencia, el kilogramo es la única unidad base del SI que tiene un prefijo SI como parte de su nombre de unidad. Se creó un estándar de kilogramo provisional y se encargó un trabajo para determinar la masa precisa de un decímetro cúbico (que más tarde se definiría como igual a un litro ) de agua. La regulación del comercio y el comercio requería una "realización práctica": un estándar de referencia metálico de una sola pieza que fuera mil veces más masivo que se conocería como la tumba . ^{[Nota 8]} Esta unidad de masa definida por Lavoisier y René Just Haüy había estado en uso desde 1793. ^[28] Esta nueva realización práctica finalmente se convertiría en la unidad base de masa. El 7 de abril de 1795, se decretó que el gramo , en el que se basa el kilogramo, era igual al «peso absoluto de un volumen de agua pura igual a un cubo de una centésima de metro, y a la temperatura del hielo derretido». ^[26] Aunque la definición del kilogramo especificaba agua a 0 °C (un punto de temperatura muy estable), se la reemplazó por la temperatura a la que el agua alcanza la densidad máxima. Esta temperatura, de unos 4 °C, no se conocía con precisión, pero una de las ventajas de la nueva definición era que el valor exacto de la temperatura en grados Celsius no era realmente importante. ^{[29] [Nota 9]} La conclusión final fue que un decímetro cúbico de agua en su densidad máxima era igual al 99,92072 % de la masa del kilogramo provisional. ^[32]

El 7 de abril de 1795, el sistema métrico decimal se definió formalmente en la legislación francesa. ^{[Nota 10]} Se definieron seis nuevas unidades decimales: ^[26]

• El metro , por longitud, definido como una diezmillonésima parte de la distancia entre el Polo Norte y el Ecuador a través de París.
• El área  (100 m ² ) es el área [de terreno]
• El estéreo  (1 m ³ ) para el volumen de leña
• El litro  (1 dm ³ ) para volúmenes de líquido
• El gramo , de masa, definida como la masa de un centímetro cúbico de agua.
• El franco , como moneda.

Nota histórica: solo el metro y el (kilo)gramo definidos aquí pasaron a formar parte de sistemas métricos posteriores. Los litros y, en menor medida, las hectáreas (100 áreas o 1 hm2 ⁾ aún se utilizan, pero no son unidades del SI.

Los múltiplos decimales de estas unidades estaban definidos por los prefijos griegos : " myria- " (10.000), " kilo- " (1000), " hecto- " (100) y " deka- " (10) y los submúltiplos estaban definidos por el latín. prefijos " deci- " (0,1), " centi- " (0,01) y " mili- " (0,001). ^[33]

Para efectos de comercio, las unidades y unidades prefijadas de peso (masa) y capacidad (volumen) podían anteponerse con los multiplicadores binarios " doble- " (2) y " demi- " ( 1 ⁄ 2 ), como en doble-litro , demi-litro ; o doble-hectogramo , demi-hectogramo , etc. ^{[Nota 11]}

Las definiciones preliminares de 1795 permitieron construir copias provisionales de los kilogramos y metros. ^{[34] [35]}

La tarea de medir el arco meridiano , que se estimó que llevaría dos años, recayó en Pierre Méchain y Jean-Baptiste Delambre . La tarea finalmente llevó más de seis años (1792-1798) con retrasos causados ​​no solo por dificultades técnicas imprevistas sino también por el convulso período posterior a la Revolución. ^[8] Aparte de las obvias consideraciones nacionalistas, el meridiano de París también fue una buena elección por razones científicas prácticas: una parte del cuadrante desde Dunkerque hasta Barcelona (unos 1000 km, o una décima parte del total) podía medirse con puntos de inicio y fin a nivel del mar, y esa parte estaba aproximadamente en el medio del cuadrante, donde se esperaba que los efectos del achatamiento de la Tierra fueran mayores. ^[20]

El proyecto se dividió en dos partes: la sección norte de 742,7 km desde el campanario de Dunkerque hasta la catedral de Rodez , que fue inspeccionada por Delambre y la sección sur de 333,0 km desde Rodez hasta la fortaleza de Montjuïc , Barcelona , ​​que fue inspeccionada por Méchain. ^{[8] : 227–230  [Nota 12]}

Delambre utilizó una línea base de unos 10 km de longitud a lo largo de una carretera recta, situada cerca de Melun . En una operación que duró seis semanas, la línea base se midió con precisión utilizando cuatro varillas de platino, cada una de dos toesas de longitud (unos 3,9 m). ^{[8] : 227–230} A partir de entonces utilizó, siempre que fue posible, los puntos de triangulación utilizados por Cassini en su reconocimiento de Francia de 1744. La línea base de Méchain, de una longitud similar, y también en una sección recta de la carretera estaba en el área de Perpiñán . ^{[8] : 240–241} Aunque el sector de Méchain tenía la mitad de la longitud de Delambre, incluía los Pirineos y partes de España hasta entonces no estudiadas. Después de que los dos topógrafos se reunieron, cada uno calculó la línea base del otro para cotejar sus resultados y luego volvieron a calcular el metro como 443,296  líneas , ^{[20] [Nota 13]} notablemente más corto que el valor provisional de 1795 de 443,44  líneas . El 15 de noviembre de 1798, Delambre y Méchain regresaron a París con sus datos, habiendo completado la medición. El valor final del metro se definió en 1799 como el valor calculado a partir de la medición.

Nota histórica: Pronto se hizo evidente que el resultado de Méchain y Delambre (443,296  líneas ) era ligeramente demasiado corto para la definición meridional del metro. Méchain había cometido un pequeño error al medir la latitud de Barcelona, ​​por lo que volvió a medirla, pero mantuvo en secreto el segundo conjunto de mediciones. ^{[Nota 14]}

En junio de 1799 se fabricaron prototipos de platino según las cantidades medidas, definiéndose el metro de archivo como una longitud de 443,296 líneas y el kilogramo de archivo como un peso de 18.827,15 granos de la libra de peso de marc ^[36] , y se introdujeron en los Archivos Nacionales de Francia. En diciembre de ese año, el sistema métrico basado en ellos se convirtió por ley en el único sistema de pesos y medidas en Francia desde 1801 hasta 1812.

A pesar de la ley, el pueblo siguió utilizando las antiguas medidas. En 1812, Napoleón revocó la ley y emitió una llamada mesures usuelles , restaurando los nombres y cantidades de las medidas habituales pero redefinidas como múltiplos redondos de las unidades métricas, por lo que era una especie de sistema híbrido. En 1837, después del colapso del Imperio napoleónico, la nueva Asamblea reimpuso el sistema métrico definido por las leyes de 1795 y 1799, para entrar en vigor en 1840. La metrificación de Francia tardó hasta aproximadamente 1858 en completarse. Algunos de los antiguos nombres de unidades, especialmente la livre , originalmente una unidad de masa derivada de la libra romana (como lo era la pound inglesa ), pero que ahora significa 500 gramos, todavía se utilizan hoy en día.

A principios del siglo XIX, los artefactos de la Academia Francesa de Ciencias para la longitud y la masa eran las únicas unidades nacientes del sistema métrico que se definían en términos de estándares formales . Otras unidades basadas en ellas, excepto el litro , resultaron ser efímeras. Los relojes de péndulo que podían medir el tiempo en segundos se habían utilizado durante unos 150 años, pero sus geometrías eran locales tanto para la latitud como para la altitud, por lo que no había un estándar de cronometraje. Tampoco se había reconocido una unidad de tiempo como unidad base esencial para la derivación de cosas como la fuerza y ​​la aceleración. Se habían identificado algunas cantidades de electricidad, como la carga y el potencial, pero aún no se habían establecido los nombres y las interrelaciones de las unidades. ^{[Nota 15]} Existían las escalas de temperatura Fahrenheit (ca. 1724) y Celsius (ca. 1742), y varios instrumentos para medir unidades o grados de ellas. El modelo de unidad base / derivada aún no se había elaborado, ni se sabía cuántas cantidades físicas podían estar interrelacionadas.

En 1861, la Asociación Británica para el Avance de la Ciencia (BAAS) propuso por primera vez un modelo de unidades interrelacionadas basado en lo que se denominó unidades "mecánicas" (longitud, masa y tiempo). Durante las décadas siguientes, esta base permitió correlacionar las unidades mecánicas , eléctricas y térmicas ^{[ ¿cuándo? ] .}

En 1832, el matemático alemán Carl-Friedrich Gauss realizó las primeras mediciones absolutas del campo magnético de la Tierra utilizando un sistema decimal basado en el uso del milímetro, el miligramo y el segundo como unidad base del tiempo. ^{[37] : 109} El segundo de Gauss se basaba en observaciones astronómicas de la rotación de la Tierra, y era el segundo sexagesimal de los antiguos: una partición del día solar en dos ciclos de 12 períodos, y cada período dividido en 60 intervalos, y cada intervalo dividido de nuevo de esa manera, de modo que un segundo era 1/86.400 del día. ^{[Nota 16]} Esto estableció efectivamente una dimensión del tiempo como un componente necesario de cualquier sistema útil de medidas, y el segundo astronómico como la unidad base.

En un artículo publicado en 1843, James Prescott Joule demostró por primera vez un medio para medir la energía transferida entre diferentes sistemas cuando se realiza trabajo, relacionando así la caloría de Nicolas Clément , definida en 1824 como "la cantidad de calor necesaria para elevar la temperatura de 1 kg de agua de 0 a 1 °C a 1 atmósfera de presión" con el trabajo mecánico . ^{[38] [39]} La energía se convirtió en el concepto unificador de la ciencia del siglo XIX , ^[40] inicialmente al unir la termodinámica y la mecánica y luego agregando la tecnología eléctrica .

En 1861, un comité de la Asociación Británica para el Avance de la Ciencia (BAAS), que incluía a William Thomson (más tarde Lord Kelvin) , James Clerk Maxwell y James Prescott Joule entre sus miembros, recibió el encargo de investigar los "Estándares de Resistencia Eléctrica". ^{[ aclaración necesaria ]} En su primer informe (1862), ^[41] establecieron las reglas básicas para su trabajo: se utilizaría el sistema métrico, las medidas de energía eléctrica debían tener las mismas unidades que las medidas de energía mecánica y se tendrían que derivar dos conjuntos de unidades electromagnéticas: un sistema electromagnético y un sistema electrostático. En el segundo informe (1863), ^[42] introdujeron el concepto de un sistema coherente de unidades mediante el cual las unidades de longitud, masa y tiempo se identificaron como "unidades fundamentales" (ahora conocidas como unidades base ). Todas las demás unidades de medida podrían derivarse (de ahí las unidades derivadas ) de estas unidades base. El metro, el gramo y el segundo fueron elegidos como unidades base. ^{[43] [44]}

En 1861, antes de ^{[ aclaración necesaria ] [ en? ]} una reunión de la BAAS, Charles Bright y Latimer Clark propusieron los nombres de ohmio , voltio y faradio en honor a Georg Ohm , Alessandro Volta y Michael Faraday respectivamente para las unidades prácticas basadas en el sistema absoluto CGS. Esto fue apoyado por Thomson (Lord Kelvin). ^[45] El concepto de nombrar unidades de medida en honor a científicos notables se utilizó posteriormente para otras unidades.

En 1873, otro comité de la BAAS (que también incluía a Maxwell y Thomson) encargado de "la selección y nomenclatura de unidades dinámicas y eléctricas" recomendó utilizar el sistema de unidades cgs . El comité también recomendó los nombres de " dina " y " erg " para las unidades cgs de fuerza y ​​energía. ^{[46] [44] [47]} El sistema cgs se convirtió en la base del trabajo científico durante los siguientes setenta años.

Los informes reconocieron dos sistemas basados ​​en centímetros-gramos-segundos para las unidades eléctricas: el sistema electromagnético (o absoluto) (EMU) y el sistema electrostático de unidades (ESU).

Símbolos utilizados en esta sección

Símbolos	Significado
${\displaystyle F_{\text{m}},F_{\text{e}}}$	Fuerzas electromagnéticas y electrostáticas
${\displaystyle I_{\text{1}},I_{\text{2}}}$	corrientes eléctricas en conductores
${\displaystyle q_{\text{1}},q_{\text{2}}}$	cargas eléctricas
${\displaystyle L}$	longitud del conductor
${\displaystyle r}$	distancia entre cargas/conductores
${\displaystyle \epsilon _{0}}$	constante eléctrica [Nota 17]
${\displaystyle \mu _{0}}$	constante magnética [Nota 17]
${\displaystyle k_{\text{m}},k_{\text{e}}}$	constantes de proporcionalidad
${\displaystyle c}$	velocidad de la luz [48]
${\displaystyle 4\pi }$	estereorradianes que rodean un punto [Nota 18]
${\displaystyle P}$	energía eléctrica
${\displaystyle V}$	potencial eléctrico
${\displaystyle I}$	corriente eléctrica
${\displaystyle E}$	energía
${\displaystyle Q}$	carga eléctrica
${\displaystyle {\mathsf {M,L,T}}}$	dimensiones: masa, longitud, tiempo

En la década de 1820, Georg Ohm formuló la Ley de Ohm , que puede extenderse para relacionar la potencia con la corriente, el potencial eléctrico (voltaje) y la resistencia. ^{[49] [50]} Durante las décadas siguientes, la realización de un sistema coherente de unidades que incorporara la medición de los fenómenos electromagnéticos y la ley de Ohm estuvo plagada de problemas: se idearon varios sistemas diferentes de unidades.

En los tres sistemas CGS, las constantes y y, en consecuencia , y eran adimensionales y, por lo tanto, no requerían ninguna unidad para definirlas.${\displaystyle k_{\text{e}}}$${\displaystyle k_{\text{m}}}$${\displaystyle \epsilon _{0}}$${\displaystyle \mu _{0}}$

Las unidades de medida eléctricas no encajaban fácilmente en el sistema coherente de unidades mecánicas definido por la BAAS. Utilizando el análisis dimensional , las dimensiones del voltaje en el sistema ESU eran idénticas a las dimensiones de la corriente en el sistema EMU, mientras que la resistencia tenía dimensiones de velocidad en el sistema EMU, pero la inversa de la velocidad en el sistema ESU. ^[44]${\displaystyle {\mathsf {M}}^{\frac {1}{2}}{\mathsf {L}}^{\frac {1}{2}}{\mathsf {T}}^{-1}}$

El sistema electromagnético de unidades (EMU) se desarrolló a partir del descubrimiento de André-Marie Ampère en la década de 1820 de una relación entre las corrientes en dos conductores y la fuerza entre ellos, ahora conocida como ley de Ampère :

${\displaystyle {\frac {F_{\text{m}}}{L}}=2k_{\text{m}}{\frac {I_{1}I_{2}}{r}}}$donde (unidades SI)${\displaystyle k_{\text{m}}={\frac {\mu _{0}}{4\pi }}\ }$

En 1833, Gauss señaló la posibilidad de equiparar esta fuerza con su equivalente mecánico. Esta propuesta recibió un nuevo apoyo de Wilhelm Weber en 1851. ^[51] En este sistema, la corriente se define fijando la fuerza magnética constante en la unidad y el potencial eléctrico se define de tal manera que se asegure que la unidad de potencia calculada por la relación sea un erg/segundo. Las unidades de medida electromagnéticas se conocían como abamperio, abvoltio, etc. ^[52] Estas unidades se escalaron posteriormente para su uso en el Sistema Internacional. ^[53]${\displaystyle k_{\mathrm {m} }}$${\displaystyle P=VI}$

El sistema electrostático de unidades (ESU) se basó en la cuantificación que Coulomb hizo en 1783 de la fuerza que actúa entre dos cuerpos cargados. Esta relación, ahora conocida como ley de Coulomb , se puede escribir

${\displaystyle F_{\mathrm {e} }=k_{\text{e}}{\frac {q_{1}q_{2}}{r^{2}}},}$donde (unidades SI)${\displaystyle k_{\text{e}}={\frac {1}{4\pi \epsilon _{0}}}}$

En este sistema, la unidad de carga se define fijando la constante de fuerza de Coulomb ( ) en la unidad y la unidad de potencial eléctrico se definió para garantizar que la unidad de energía calculada por la relación sea un erg. Las unidades de medida electrostáticas fueron el estatamperio, el estatavoltio, etc. ^[54]${\displaystyle k_{\text{e}}}$${\displaystyle E=QV}$

El sistema gaussiano de unidades se basó en la constatación de Heinrich Hertz , ^{[ cita requerida ]} al verificar las ecuaciones de Maxwell en 1888, de que las unidades electromagnéticas y electrostáticas estaban relacionadas por:

${\displaystyle c^{2}={\frac {1}{\epsilon _{0}\mu _{0}}}}$^{[55] [56]}

Utilizando esta relación, propuso fusionar los sistemas EMU y ESU en un solo sistema utilizando las unidades EMU para magnitudes magnéticas (posteriormente llamadas gauss y maxwell ) y las unidades ESU en otros lugares. Llamó a este conjunto combinado de unidades " unidades gaussianas ". Este conjunto de unidades ha sido reconocido por ser particularmente útil en física teórica. ^{[37] : 128}

Las unidades de medida del CGS utilizadas en el trabajo científico no eran prácticas para la ingeniería, lo que llevó al desarrollo de un sistema más aplicable de unidades eléctricas, especialmente para la telegrafía. La unidad de longitud era 10 ⁷  m (el hebdómetro , nominalmente el cuadrante terrestre ), la unidad de masa era una unidad sin nombre igual a 10 ⁻¹¹  g y la unidad de tiempo era el segundo. Las unidades de masa y longitud se escalaron de manera incongruente para producir unidades eléctricas más consistentes y utilizables en términos de medidas mecánicas. Denominado informalmente el sistema "práctico", se denominó correctamente el sistema de unidades de cuadrante-onceésimo gramo-segundo (QES) según la convención.

Las definiciones de unidades eléctricas incorporaron la constante magnética como el sistema EMU, y los nombres de las unidades fueron transferidos de ese sistema, pero escalados de acuerdo con las unidades mecánicas definidas. ^[57] El sistema se formalizó como el sistema internacional a fines del siglo XIX y sus unidades luego se designaron como "amperio internacional", "voltio internacional", etc. ^{[58] : 155–156}

El factor que aparece en las ecuaciones de Maxwell en el sistema gaussiano (y en los demás sistemas CGS) proviene de los estereorradianes que rodean un punto, como una carga eléctrica puntual. Este factor podría eliminarse de los contextos que no implican coordenadas esféricas incorporando el factor en las definiciones de las cantidades involucradas. El sistema fue propuesto por Oliver Heaviside en 1883 y también se lo conoce como el "sistema de unidades gaussiano racionalizado". Posteriormente, el SI adoptó unidades racionalizadas basadas en el esquema de racionalización de Heaviside.${\displaystyle 4\pi }$${\displaystyle 4\pi }$

Maxwell y Boltzmann habían elaborado teorías que describían la interrelación entre la temperatura, la presión y el volumen de un gas a escala microscópica, pero, en 1900, no se entendía la naturaleza microscópica de la temperatura. ^{[59] [60]}

A finales del siglo XIX, se habían formulado las leyes macroscópicas fundamentales de la termodinámica y, aunque existían técnicas para medir la temperatura utilizando técnicas empíricas, la comprensión científica ^{[ aclaración necesaria ]} de la naturaleza de la temperatura era mínima.

Con la creciente adopción internacional del metro, las deficiencias del mètre des Archives como estándar se hicieron cada vez más evidentes. Los países que adoptaron el metro como medida legal compraron barras de metro estándar que se suponía que tenían la misma longitud que el mètre des Archives , pero no había una manera sistemática de garantizar que los países estuvieran trabajando realmente con el mismo estándar. La definición meridional, que se había pensado para garantizar la reproducibilidad internacional, pronto resultó tan poco práctica que casi se abandonó en favor de los estándares de artefactos, pero el mètre des Archives (y la mayoría de sus copias) eran "estándares finales": dichos estándares (barras que tienen exactamente un metro de longitud) son propensos a desgastarse con el uso, y se podía esperar que las diferentes barras estándar se desgastaran a diferentes velocidades. ^[61]

En 1867 se propuso la creación de un nuevo metro patrón internacional, y se consideró que su longitud sería la del metro de los Archivos "en el estado en que se encuentre". ^{[62] [63]} La Conferencia Internacional de Geodesia de 1867 pidió la creación de un nuevo prototipo internacional del metro ^{[62] [63] [Nota 19]} y de un sistema mediante el cual se pudieran comparar los patrones nacionales con él. El prototipo internacional también sería un "patrón de línea", es decir, el metro se definía como la distancia entre dos líneas marcadas en la barra, evitando así los problemas de desgaste de los patrones de extremo. El gobierno francés dio apoyo práctico a la creación de una Comisión Internacional del Metro, que se reunió en París en 1870 y nuevamente en 1872 con la participación de unos treinta países. ^[62]

El 20 de mayo de 1875, 17 estados firmaron un tratado internacional conocido como la Convención del Metro ^{. [21] [64]} Este tratado estableció las siguientes organizaciones para llevar a cabo actividades internacionales relacionadas con un sistema uniforme de mediciones:

• Conferencia General de Pesas y Medidas (CGPM), conferencia intergubernamental de delegados oficiales de los países miembros y autoridad suprema para todas las acciones;
• Comité Internacional de Pesas y Medidas (CIPM o Comité Internacional de Pesas y Medidas), integrado por científicos y metrólogos seleccionados , que prepara y ejecuta las decisiones de la CGPM y es responsable de la supervisión de la Oficina Internacional de Pesas y Medidas;
• Oficina Internacional de Pesas y Medidas (BIPM), laboratorio permanente y centro mundial de metrología científica, cuyas actividades incluyen el establecimiento de los patrones y escalas básicos de las principales magnitudes físicas, el mantenimiento de los patrones prototipo internacionales y la supervisión de las comparaciones periódicas entre el prototipo internacional y los diversos patrones nacionales.

El prototipo internacional del metro y el prototipo internacional del kilogramo se fabricaron a partir de una  aleación de 90% platino y 10%  iridio , que es excepcionalmente dura y tiene buenas propiedades de conductividad eléctrica y térmica. El prototipo tenía una sección transversal especial en forma de X ( Tresca ) para minimizar los efectos de la tensión torsional durante las comparaciones de longitud ^[21] y los kilogramos prototipo tenían forma cilíndrica. La firma londinense Johnson Matthey entregó 30 metros prototipo y 40 kilogramos prototipo. En la primera reunión de la CGPM en 1889, la barra n.° 6 y el cilindro n.° X fueron aceptados como prototipos internacionales. El resto se mantuvieron como copias de trabajo de la BIPM o se distribuyeron a los estados miembros como prototipos nacionales. ^[65]

Tras la Convención del Metro, en 1889, el BIPM tenía en su poder dos artefactos: uno para definir la longitud y el otro para definir la masa. Otras unidades de medida que no dependían de artefactos específicos estaban controladas por otros organismos.

Aunque la definición del kilogramo se mantuvo inalterada a lo largo del siglo XX, la 3.ª CGPM de 1901 aclaró que el kilogramo era una unidad de masa , no de peso . El lote original de 40 prototipos (adoptado en 1889) se complementó de vez en cuando con otros prototipos para su uso por parte de los nuevos signatarios de la Convención del Metro . ^[66]

En 1921, el Tratado del Metro se amplió para cubrir las unidades eléctricas y la CGPM fusionó su trabajo con el de la IEC.

La historia de la medición en el siglo XX está marcada por cinco períodos: la definición de 1901 del sistema coherente MKS; los 50 años intermedios de coexistencia del MKS, el cgs y los sistemas comunes de medidas; el prototipo del sistema práctico de unidades del SI de 1948; la introducción del SI en 1960; y la evolución del SI en el segundo medio siglo.

Giorgi identificó la necesidad de una dimensión electromagnética independiente para resolver las dificultades relacionadas con la definición de tales unidades en términos de longitud, masa y tiempo en 1901. Esto llevó a Giorgi a presentar un artículo en octubre de 1901 en el congreso de la Associazione Elettrotecnica Italiana (AEI) ^[67] en el que demostró que se podía obtener un sistema electromecánico coherente de unidades añadiendo una cuarta unidad base de naturaleza eléctrica (por ejemplo, amperio, voltio u ohmio) a las tres unidades base propuestas en el informe BAAS de 1861. Esto dio dimensiones físicas a las constantes k _e y k _m y, por lo tanto, también a las cantidades electromecánicas ε ₀ (permitividad del espacio libre) y μ ₀ (permeabilidad del espacio libre). ^[68] Su trabajo también reconoció la relevancia de la energía en el establecimiento de un sistema coherente y racional de unidades, con el joule como unidad de energía y las unidades eléctricas en el Sistema Internacional de Unidades permaneciendo sin cambios. ^{[58] : 156} Sin embargo, pasaron más de treinta años antes de que el trabajo de Giorgi fuera aceptado en la práctica por la IEC.

A medida que la industria se fue desarrollando en todo el mundo, el sistema de unidades cgs adoptado por la Asociación Británica para el Avance de la Ciencia en 1873, con su plétora de unidades eléctricas, siguió siendo el sistema de medición dominante, y así permaneció al menos durante los siguientes 60 años. Las ventajas eran varias: tenía un conjunto completo de unidades derivadas que, si bien no eran del todo coherentes, eran al menos homólogas; el sistema MKS carecía de una unidad definida de electromagnetismo; las unidades MKS eran incómodamente grandes para las ciencias; los sistemas de medidas tradicionales prevalecían en los Estados Unidos, Gran Bretaña y el imperio británico, e incluso en cierta medida en Francia, la cuna del sistema métrico, lo que inhibía la adopción de cualquier sistema competidor. Finalmente, la guerra, el nacionalismo y otras fuerzas políticas inhibieron el desarrollo de la ciencia en favor de un sistema coherente de unidades.

En la 8.ª CGPM de 1933 se planteó la necesidad de sustituir las unidades eléctricas "internacionales" por unidades "absolutas". Se aceptó la propuesta de la IEC de adoptar el "sistema" de Giorgi, denominado informalmente MKSX, pero no se tomó ninguna decisión sobre qué unidad eléctrica debería ser la cuarta unidad básica. En 1935, JE Sears ^{[69] [ cita requerida ]} propuso que esta debería ser el amperio, pero la Segunda Guerra Mundial impidió que se formalizara hasta 1946. La primera (y única) comparación de seguimiento de los patrones nacionales con el prototipo internacional del metro se llevó a cabo entre 1921 y 1936, ^{[21] [63]} e indicó que la definición del metro se conservaba con una precisión de 0,2 μm. ^[70] Durante esta comparación de seguimiento, se definió más claramente la forma en que se debe medir el metro prototipo: la definición de 1889 había definido el metro como la longitud del prototipo a la temperatura de fusión del hielo, pero, en 1927, la 7.ª CGPM amplió esta definición para especificar que el metro prototipo debe estar "apoyado en dos cilindros de al menos un centímetro de diámetro, colocados simétricamente en el mismo plano horizontal a una distancia de 571 mm uno del otro". ^{[37] : 142–43, 148} La elección de 571 mm representa los puntos de Airy del prototipo, los puntos en los que se minimiza la flexión o caída de la barra. ^[71]

La 9.ª CGPM se reunió en 1948, quince años después de la 8.ª CGPM. En respuesta a las solicitudes formales realizadas por la Unión Internacional de Física Pura y Aplicada y por el gobierno francés para establecer un sistema práctico de unidades de medida, la CGPM solicitó al CIPM que preparara recomendaciones para un sistema práctico único de unidades de medida, adecuado para su adopción por todos los países que se adhirieran a la Convención del Metro. ^[72] El proyecto de propuesta del CIPM era una revisión y simplificación exhaustiva de las definiciones, símbolos y terminología de las unidades métricas basadas en el sistema de unidades MKS.

Tras las observaciones astronómicas, el segundo se fijó como una fracción del año 1900. La unidad básica electromagnética, tal como exigía Giorgi, fue aceptada como el amperio. Tras las negociaciones con la CEI y la IUPAP, se propusieron también como unidades básicas dos unidades adicionales: el grado kelvin y la candela. ^[73] Por primera vez, la CGPM hizo recomendaciones sobre las unidades derivadas. Al mismo tiempo, la CGPM adoptó convenciones para la escritura e impresión de símbolos y números de unidades y catalogó los símbolos de las unidades de medida MKS y CGS más importantes . ^[74]

Hasta la llegada del reloj atómico , el cronómetro más fiable de que disponía la humanidad era la rotación de la Tierra. Por tanto, era natural que los astrónomos, bajo los auspicios de la Unión Astronómica Internacional (UAI), asumieran el liderazgo en el mantenimiento de los estándares relacionados con el tiempo. Durante el siglo XX, se hizo evidente que la rotación de la Tierra se estaba ralentizando, lo que hacía que los días fueran 1,4 milisegundos más largos cada siglo ^[75] —esto se verificó comparando los tiempos calculados de los eclipses de Sol con los observados en la antigüedad que se remontan a los registros chinos del 763 a. C. ^[76] En 1956, la 10.ª CGPM encargó al CIPM que preparara una definición del segundo; en 1958, se publicó la definición que establecía que el segundo (llamado segundo de efemérides ) se calcularía por extrapolación utilizando la velocidad de rotación de la Tierra en 1900. ^[75]

En las propuestas de Per Giorgi de 1901, el CIPM también recomendó que el amperio fuera la unidad base de la que se derivarían las unidades electromecánicas. Las definiciones de ohmio y voltio que se habían utilizado anteriormente se descartaron, y estas unidades se convirtieron en unidades derivadas basadas en el amperio. En 1946, el CIPM adoptó formalmente una definición del amperio basada en la definición original de la UEM y redefinió el ohmio en términos de otras unidades base. ^[77] Las definiciones para el sistema eléctrico absoluto, ^{[ aclaración necesaria ]} basadas en el amperio, se formalizaron en 1948. ^[78] Las unidades propuestas en el borrador con estos nombres son muy cercanas, pero no idénticas, a las unidades internacionales. ^[79]

En la escala Celsius del siglo XVIII, la temperatura se expresaba en grados Celsius con la definición de que el hielo se derretía a 0 °C y (a presión atmosférica estándar) el agua hervía a 100 °C. Una serie de tablas de consulta definían la temperatura en términos de mediciones empíricas interrelacionadas realizadas utilizando varios dispositivos. En 1948, se tuvieron que aclarar las definiciones relacionadas con la temperatura. (El grado, como medida angular, fue adoptado para uso general en muchos países, por lo que, en 1948, la Conferencia General de Pesas y Medidas (CGPM) recomendó que el grado Celsius, tal como se usa para la medición de la temperatura, se cambiara de nombre a grado Celsius .) ^[80]

En la 9ª CGPM, la escala de temperatura Celsius pasó a llamarse escala Celsius , y la escala en sí se fijó definiendo el punto triple del agua como 0,01 °C, ^[81] aunque la CGPM dejó la definición formal del cero absoluto hasta la 10ª CGPM, cuando se asignó el nombre " Kelvin " a la escala de temperatura absoluta, y el punto triple del agua se definió como 273,16 °K. ^[82]

Antes de 1937, la Comisión Internacional del Alumbrado ( CIE ), en colaboración con el CIPM, elaboró ​​una norma de intensidad luminosa que sustituyó a las diversas normas nacionales. Esta norma, la candela (cd), definida como «la luminosidad del radiador lleno a la temperatura de solidificación del platino de 60 nuevas candelas por centímetro cuadrado », ^[83] fue ratificada por la CGPM en 1948.

La nueva definición del amperio permitió definir de manera práctica y útil un conjunto de unidades derivadas del sistema electromagnético, entre ellas el faradio, el henrio, el vatio, el tesla, el weber, el voltio, el ohmio y el culombio. Dos unidades derivadas, el lux y el lumen, se basaron en la nueva candela, y una, el grado Celsius, equivalente al grado Kelvin. Otras cinco unidades derivadas diversas completaron la propuesta preliminar: el radián, el estereorradián, el hercio, el julio y el newton.

En 1952, el CIPM propuso utilizar la longitud de onda de una fuente de luz específica como patrón para definir la longitud y, en 1960, la CGPM aceptó esta propuesta utilizando la radiación correspondiente a una transición entre niveles de energía específicos del átomo de kriptón 86 como el nuevo patrón para el metro. El artefacto del metro patrón fue retirado.

En 1960, las propuestas de Giorgi fueron adoptadas como base del Sistema Internacional de Unidades , el SI. ^{[37] : 109} Esta definición inicial del SI incluía seis unidades base, el metro, el kilogramo, el segundo, el amperio, el grado Kelvin y la candela, y dieciséis unidades derivadas coherentes. ^[84]

La evolución del SI después de su publicación en 1960 ha visto la adición de una séptima unidad básica, el mol , y seis unidades derivadas más, el pascal para la presión, el gray , el sievert y el becquerel para la radiación, el siemens para la conductancia eléctrica y el katal para la actividad catalítica (enzimática). Varias unidades también se han redefinido en términos de constantes físicas.

Durante los años siguientes, el BIPM desarrolló y mantuvo correlaciones cruzadas que relacionaban varios dispositivos de medición, como termopares, espectros de luz y similares, con las temperaturas equivalentes. ^[85]

El mol se conocía originalmente como un átomo-gramo o una molécula-gramo: la cantidad de una sustancia medida en gramos dividida por su peso atómico . Originalmente, los químicos y los físicos tenían diferentes puntos de vista con respecto a la definición del peso atómico: ambos asignaban un valor de 16  unidades de masa atómica (uma) al oxígeno, pero los físicos definían el oxígeno en términos del isótopo ¹⁶ O, mientras que los químicos asignaban 16 uma a los isótopos ¹⁶ O, ¹⁷ O y ¹⁸ O mezclados en la proporción en que ocurren en la naturaleza. Finalmente, un acuerdo entre la Unión Internacional de Física Pura y Aplicada ^[86] (IUPAP) y la Unión Internacional de Química Pura y Aplicada (IUPAC) puso fin a esta dualidad en 1959/60, y ambas partes acordaron definir el peso atómico de ¹² C como exactamente 12 uma. Este acuerdo fue confirmado por la ISO y en 1969 el CIPM recomendó su inclusión en el SI como unidad base. Esto se hizo en 1971 en la 14ª CGPM. ^{[37] : 114–115}

La segunda tendencia importante en el SI posmoderno fue la migración de las definiciones de unidades en términos de constantes físicas de la naturaleza.

En 1967, en la 13ª CGPM, el grado Kelvin (°K) pasó a llamarse "kelvin" (K). ^[87]

Astrónomos del Observatorio Naval de Estados Unidos (USNO) y del Laboratorio Nacional de Física determinaron una relación entre la frecuencia de radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del átomo de cesio 133 y la tasa estimada de rotación de la Tierra en 1900. Su definición atómica del segundo fue adoptada en 1968 por la 13ª CGPM.

En 1975, cuando el segundo se había definido en términos de un fenómeno físico y no de la rotación de la Tierra, la CGPM autorizó al CIPM a investigar el uso de la velocidad de la luz como base para la definición del metro. Esta propuesta fue aceptada en 1983. ^[88]

La definición de candela resultó difícil de implementar, por lo que en 1979 se revisó la definición y se reemplazó la referencia a la fuente de radiación por la definición de la candela en términos de la potencia de una frecuencia específica de luz visible monocromática de color verde amarillento, ^{[37] : 115} , que está cerca de la frecuencia en la que el ojo humano, cuando se adapta a condiciones brillantes, tiene mayor sensibilidad.

Tras la redefinición del metro en 1960, el kilogramo siguió siendo la única unidad base del SI definida mediante un artefacto físico. Durante los años siguientes, se fueron perfeccionando las definiciones de las unidades base y, en particular, la puesta en práctica ^[90] para hacer realidad esas definiciones.

La tercera recalibración periódica, realizada entre 1988 y 1989, reveló que la diferencia media entre el IPK y la línea de base ajustada para los prototipos nacionales era de 50 μg (en 1889, la línea de base de los prototipos nacionales se había ajustado de modo que la diferencia fuera cero). Como el IPK es el kilogramo definitivo, no hay forma de saber si el IPK había estado perdiendo masa o si los prototipos nacionales habían estado ganando masa. ^[89]

A lo largo del siglo, los distintos prototipos nacionales del kilogramo se recalibraron en relación con el prototipo internacional del kilogramo (IPK) y, por lo tanto, entre sí. Las desviaciones iniciales de los valores de partida de 1889 de los prototipos nacionales en relación con el IPK se anularon ^[89] y todos los cambios de masa posteriores se hicieron en relación con el IPK.

Se propusieron varios sustitutos para el IPK.

Desde principios de los años 1990, el Proyecto Internacional Avogadro trabajó en la creación de una esfera de 1 kg y 94 mm hecha de un cristal uniforme de silicio-28, con la intención de poder reemplazar el IPK por un objeto físico que pudiera reproducirse con precisión a partir de una especificación exacta. Debido a su construcción precisa, es probable que la esfera del Proyecto Avogadro sea el objeto más esférico creado por el ser humano. ^[91]

Otros grupos trabajaron en conceptos como la creación de una masa de referencia mediante la electrodeposición precisa de átomos de oro o bismuto, y la definición del kilogramo en términos del amperio relacionándolo con fuerzas generadas por la repulsión electromagnética de corrientes eléctricas. ^[92]

Al final, las opciones se redujeron al uso de la balanza de Watt y la esfera del Proyecto Internacional Avogadro. ^[92]

Finalmente, se tomó la decisión de no crear ningún reemplazo físico para el IPK, sino definir todas las unidades del SI en términos de asignar valores precisos a una serie de constantes físicas que previamente se habían medido en términos de las definiciones de unidades anteriores.

En su 23ª reunión (2007), la CGPM encargó al CIPM que investigara el uso de constantes naturales como base para todas las unidades de medida en lugar de los artefactos que se utilizaban entonces.

El año siguiente, la Unión Internacional de Física Pura y Aplicada (IUPAP) aprobó esta propuesta . ^[93] En una reunión de la CCU celebrada en Reading (Reino Unido ) en septiembre de 2010, se acordó en principio una resolución ^[94] y un borrador de cambios al folleto del SI que se presentarían en la siguiente reunión del CIPM en octubre de 2010. ^[95] La reunión del CIPM de octubre de 2010 concluyó que "las condiciones establecidas por la Conferencia General en su 23.ª reunión aún no se han cumplido plenamente. ^{[Nota 21]} Por esta razón, el CIPM no propone una revisión del SI en este momento". ^[97] Sin embargo, el CIPM presentó una resolución para su consideración en la 24.ª CGPM (17-21 de octubre de 2011) para acordar las nuevas definiciones en principio, pero no para implementarlas hasta que se hubieran ultimado los detalles. ^[98]

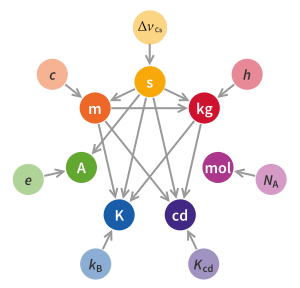
En la revisión, cuatro de las siete unidades básicas del SI (el kilogramo , el amperio , el kelvin y el mol) se redefinieron estableciendo valores numéricos exactos para la constante de Planck ( h ), la carga eléctrica elemental ( e ), la constante de Boltzmann ( k _B ) y la constante de Avogadro ( N _A ), respectivamente. El segundo , el metro y la candela ya estaban definidos como constantes físicas y estaban sujetos a corrección en sus definiciones. Las nuevas definiciones apuntaban a mejorar el SI sin cambiar el valor de ninguna unidad, asegurando la continuidad con las mediciones existentes. ^{[99] [100]}

Esta resolución fue aceptada por la conferencia, ^[101] y, además, la CGPM adelantó la fecha de la 25ª reunión de 2015 a 2014. ^{[102] [103]} En la 25ª reunión del 18 al 20 de noviembre de 2014, se encontró que "a pesar [del progreso en los requisitos necesarios] los datos aún no parecen ser suficientemente robustos para que la CGPM adopte la SI revisada en su 25ª reunión", ^[104] posponiendo así la revisión a la siguiente reunión en 2018.

En 2017 se disponía de mediciones suficientemente precisas para cumplir las condiciones y la revisión ^[105] se adoptó en la 26.ª CGPM (13-16 de noviembre de 2018), y los cambios entraron finalmente en vigor en 2019, creando un sistema de definiciones que pretende ser estable a largo plazo.

• Historia del metro
• Historia de la medición
• Paso al sistema métrico