Politopo complejo
This article has problems which may render some text or images unreadable or difficult to read in dark mode. Desktop readers can switch to light mode temporarily using the eyeglasses icon at the top of the page. (September 2024) |
En geometría , un politopo complejo es una generalización de un politopo en el espacio real a una estructura análoga en un espacio de Hilbert complejo , donde cada dimensión real está acompañada por una imaginaria .
Un politopo complejo puede entenderse como una colección de puntos, líneas, planos, etc. complejos, donde cada punto es la unión de múltiples líneas, cada línea de múltiples planos, y así sucesivamente.
Sólo existen definiciones precisas para los politopos complejos regulares, que son configuraciones . Los politopos complejos regulares han sido completamente caracterizados y pueden describirse utilizando una notación simbólica desarrollada por Coxeter .
También se han descrito algunos politopos complejos que no son totalmente regulares.
Definiciones e introducción
La línea compleja tiene una dimensión con coordenadas reales y otra con coordenadas imaginarias . Se dice que al aplicar coordenadas reales a ambas dimensiones se obtienen dos dimensiones sobre los números reales. Un plano real, con el eje imaginario etiquetado como tal, se denomina diagrama de Argand . Por eso, a veces se lo denomina plano complejo. El espacio complejo de 2 dimensiones (también llamado a veces plano complejo) es, por tanto, un espacio de cuatro dimensiones sobre los números reales, y así sucesivamente en dimensiones superiores.
Un politopo complejo n en un espacio n complejo es el análogo de un politopo real n en un espacio n real . Sin embargo, no existe un análogo complejo natural del ordenamiento de los puntos en una línea real (ni de las propiedades combinatorias asociadas). Por ello, un politopo complejo no puede verse como una superficie contigua y no limita un interior como lo hace un politopo real.
En el caso de los politopos regulares , se puede hacer una definición precisa utilizando la noción de simetría. Para cualquier politopo regular , el grupo de simetría (aquí un grupo de reflexión complejo , llamado grupo de Shephard ) actúa transitivamente sobre los flags , es decir, sobre las sucesiones anidadas de un punto contenido en una línea contenida en un plano, y así sucesivamente.
De manera más completa, digamos que una colección P de subespacios afines (o planos ) de un espacio unitario complejo V de dimensión n es un politopo complejo regular si cumple las siguientes condiciones: [1] [2]
- para cada −1 ≤ i < j < k ≤ n , si F es un plano en P de dimensión i y H es un plano en P de dimensión k tal que F ⊂ H entonces hay al menos dos planos G en P de dimensión j tales que F ⊂ G ⊂ H ;
- para cada i , j tales que −1 ≤ i < j − 2, j ≤ n , si F ⊂ G son planos de P de dimensiones i , j , entonces el conjunto de planos entre F y G es conexo, en el sentido de que se puede llegar desde cualquier miembro de este conjunto a cualquier otro mediante una secuencia de contenciones; y
- el subconjunto de transformaciones unitarias de V que fijan P son transitivas sobre las banderas F 0 ⊂ F 1 ⊂ … ⊂ F n de planos de P (con F i de dimensión i para todo i ).
(Aquí, un plano de dimensión −1 se toma como el conjunto vacío.) Por lo tanto, por definición, los politopos complejos regulares son configuraciones en el espacio unitario complejo.
Los politopos complejos regulares fueron descubiertos por Shephard (1952) y la teoría fue desarrollada posteriormente por Coxeter (1974).
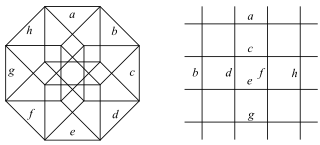 Este polígono complejo tiene 8 aristas (líneas complejas), etiquetadas como .. h , y 16 vértices. Cuatro vértices se encuentran en cada arista y dos aristas se intersecan en cada vértice. En la imagen de la izquierda, los cuadrados delineados no son elementos del politopo, sino que se incluyen simplemente para ayudar a identificar los vértices que se encuentran en la misma línea compleja. El perímetro octagonal de la imagen de la izquierda no es un elemento del politopo, sino un polígono de Petrie . [3] En la imagen del medio, cada arista se representa como una línea real y los cuatro vértices de cada línea se pueden ver más claramente. | 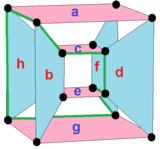 Un boceto en perspectiva que representa los 16 vértices como grandes puntos negros y las 8 aristas de 4 lados como cuadrados delimitados dentro de cada arista. El camino verde representa el perímetro octogonal de la imagen de la izquierda. |
Un politopo complejo existe en el espacio complejo de dimensión equivalente. Por ejemplo, los vértices de un polígono complejo son puntos en el plano complejo (un plano en el que cada punto tiene dos números complejos como coordenadas, que no debe confundirse con el plano de Argand de números complejos), y las aristas son líneas complejas que existen como subespacios (afines) del plano y se intersecan en los vértices. Por lo tanto, como espacio complejo unidimensional, a una arista se le puede dar su propio sistema de coordenadas, dentro del cual los puntos de la arista están representados cada uno por un solo número complejo.
En un politopo complejo regular, los vértices incidentes en la arista están dispuestos simétricamente respecto de su centroide , que a menudo se utiliza como el origen del sistema de coordenadas de la arista (en el caso real, el centroide es simplemente el punto medio de la arista). La simetría surge de una reflexión compleja sobre el centroide; esta reflexión dejará la magnitud de cualquier vértice sin cambios, pero cambiará su argumento en una cantidad fija, moviéndolo a las coordenadas del siguiente vértice en orden. Por lo tanto, podemos suponer (después de una elección adecuada de la escala) que los vértices en la arista satisfacen la ecuación donde p es el número de vértices incidentes. Por lo tanto, en el diagrama de Argand de la arista, los puntos de vértice se encuentran en los vértices de un polígono regular centrado en el origen.
Arriba se ilustran tres proyecciones reales del polígono complejo regular 4{4}2, con aristas a, b, c, d, e, f, g, h . Tiene 16 vértices, que para mayor claridad no se han marcado individualmente. Cada arista tiene cuatro vértices y cada vértice se encuentra sobre dos aristas, por lo tanto, cada arista se encuentra con otras cuatro aristas. En el primer diagrama, cada arista está representada por un cuadrado. Los lados del cuadrado no son partes del polígono, sino que se dibujan simplemente para ayudar a relacionar visualmente los cuatro vértices. Las aristas están dispuestas simétricamente. (Obsérvese que el diagrama parece similar a la proyección del plano de Coxeter B 4 del teseracto , pero es estructuralmente diferente).
El diagrama central abandona la simetría octogonal en favor de la claridad. Cada arista se muestra como una línea real y cada punto de encuentro de dos líneas es un vértice. La conectividad entre las distintas aristas es evidente.
El último diagrama da una idea de la estructura proyectada en tres dimensiones: los dos cubos de vértices son de hecho del mismo tamaño, pero se ven en perspectiva a diferentes distancias en la cuarta dimensión.
Politopos regulares complejos unidimensionales

Un politopo unidimensional real existe como un segmento cerrado en la línea real , definido por sus dos puntos finales o vértices en la línea. Su símbolo de Schläfli es {} .
De manera análoga, un politopo 1 complejo existe como un conjunto de p puntos de vértice en la línea compleja . Estos pueden representarse como un conjunto de puntos en un diagrama de Argand ( x , y )= x + iy . Un politopo regular complejo unidimensional p {} tiene p ( p ≥ 2) puntos de vértice dispuestos para formar un polígono regular convexo { p } en el plano de Argand. [4]
A diferencia de los puntos de la línea real, los puntos de la línea compleja no tienen un orden natural. Por lo tanto, a diferencia de los politopos reales, no se puede definir ningún interior. [5] A pesar de esto, los 1-politopos complejos a menudo se dibujan, como aquí, como un polígono regular acotado en el plano de Argand.

Un politopo real regular unidimensional se representa mediante un símbolo de Schläfli vacío {}, o diagrama de Coxeter-Dynkin  El punto o nodo del diagrama de Coxeter-Dynkin representa en sí mismo un generador de reflexión, mientras que el círculo alrededor del nodo significa que el punto generador no está en la reflexión, por lo que su imagen reflejada es un punto distinto de sí mismo. Por extensión, un politopo regular complejo unidimensional en tiene diagrama de Coxeter-Dynkin
El punto o nodo del diagrama de Coxeter-Dynkin representa en sí mismo un generador de reflexión, mientras que el círculo alrededor del nodo significa que el punto generador no está en la reflexión, por lo que su imagen reflejada es un punto distinto de sí mismo. Por extensión, un politopo regular complejo unidimensional en tiene diagrama de Coxeter-Dynkin  , para cualquier entero positivo p , 2 o mayor, que contenga p vértices. p se puede suprimir si es 2. También se puede representar mediante un símbolo de Schläfli vacío p {}, } p {, {} p o p {2} 1 . El 1 es un marcador de posición de notación, que representa una reflexión inexistente o un generador de identidad de período 1. (Un politopo 0, real o complejo es un punto y se representa como } { o 1 {2} 1 ).
, para cualquier entero positivo p , 2 o mayor, que contenga p vértices. p se puede suprimir si es 2. También se puede representar mediante un símbolo de Schläfli vacío p {}, } p {, {} p o p {2} 1 . El 1 es un marcador de posición de notación, que representa una reflexión inexistente o un generador de identidad de período 1. (Un politopo 0, real o complejo es un punto y se representa como } { o 1 {2} 1 ).
La simetría se denota mediante el diagrama de Coxeter.  , y puede describirse alternativamente en notación de Coxeter como p [], [] p o ] p [, p [2] 1 o p [1] p . La simetría es isomorfa al grupo cíclico , orden p . [6] Los subgrupos de p [] son cualquier divisor entero d , d [], donde d ≥2.
, y puede describirse alternativamente en notación de Coxeter como p [], [] p o ] p [, p [2] 1 o p [1] p . La simetría es isomorfa al grupo cíclico , orden p . [6] Los subgrupos de p [] son cualquier divisor entero d , d [], donde d ≥2.
Un generador de operador unitario para se ve como una rotación de 2π/ p radianes en sentido antihorario y una
se ve como una rotación de 2π/ p radianes en sentido antihorario y una El borde se crea mediante aplicaciones secuenciales de una única reflexión unitaria. Un generador de reflexión unitaria para un 1-politopo con p vértices es e 2π i / p = cos(2π/ p ) + i sin(2π/ p ) . Cuando p = 2, el generador es e π i = –1, lo mismo que una reflexión puntual en el plano real.
El borde se crea mediante aplicaciones secuenciales de una única reflexión unitaria. Un generador de reflexión unitaria para un 1-politopo con p vértices es e 2π i / p = cos(2π/ p ) + i sin(2π/ p ) . Cuando p = 2, el generador es e π i = –1, lo mismo que una reflexión puntual en el plano real.
En politopos de mayor complejidad, los politopos 1 forman aristas p . Una arista 2 es similar a una arista real ordinaria, en el sentido de que contiene dos vértices, pero no necesita existir en una línea real.
Polígonos regulares complejos
Mientras que los 1-politopos pueden tener p ilimitados , los polígonos complejos regulares finitos, excluyendo los polígonos de prisma doble p {4} 2 , están limitados a elementos de 5 aristas (aristas pentagonales), y los apeirógonos regulares infinitos también incluyen elementos de 6 aristas (aristas hexagonales).
Notaciones
Notación Schläfli modificada de Shephard
Shephard ideó originalmente una forma modificada de la notación de Schläfli para politopos regulares. Para un polígono delimitado por p 1 -aristas, con un p 2 -conjunto como figura de vértice y un grupo de simetría general de orden g , denotamos el polígono como p 1 ( g ) p 2 .
El número de vértices V es entonces g / p 2 y el número de aristas E es g / p 1 .
El polígono complejo ilustrado arriba tiene ocho aristas cuadradas ( p 1 = 4) y dieciséis vértices ( p 2 = 2). De esto podemos deducir que g = 32, lo que da el símbolo de Schläfli modificado 4(32)2.
Notación Schläfli modificada revisada de Coxeter
Una notación más moderna p 1 { q } p 2 se debe a Coxeter , [7] y se basa en la teoría de grupos. Como grupo de simetría, su símbolo es p 1 [ q ] p 2 .
El grupo de simetría p 1 [ q ] p 2 está representado por 2 generadores R 1 , R 2 , donde: R 1 p 1 = R 2 p 2 = I. Si q es par, (R 2 R 1 ) q /2 = (R 1 R 2 ) q /2 . Si q es impar, (R 2 R 1 ) (q−1)/2 R 2 = (R 1 R 2 ) ( q −1)/2 R 1 . Cuando q es impar, p 1 = p 2 .
Para 4 [4] 2 tiene R 1 4 = R 2 2 = I, (R 2 R 1 ) 2 = (R 1 R 2 ) 2 .
Para 3 [5] 3 tiene R 1 3 = R 2 3 = I, (R 2 R 1 ) 2 R 2 = (R 1 R 2 ) 2 R 1 .
Diagramas de Coxeter-Dynkin
Coxeter también generalizó el uso de los diagramas de Coxeter-Dynkin a politopos complejos, por ejemplo, el polígono complejo p { q } r se representa mediante

 y el grupo de simetría equivalente, p [ q ] r , es un diagrama sin anillo
y el grupo de simetría equivalente, p [ q ] r , es un diagrama sin anillo

 Los nodos p y r representan espejos que producen imágenes p y r en el plano. Los nodos sin etiquetar en un diagrama tienen etiquetas 2 implícitas. Por ejemplo, un polígono regular real es 2 { q } 2 o { q } o
Los nodos p y r representan espejos que producen imágenes p y r en el plano. Los nodos sin etiquetar en un diagrama tienen etiquetas 2 implícitas. Por ejemplo, un polígono regular real es 2 { q } 2 o { q } o

 .
.
Una limitación: los nodos conectados por órdenes de ramificación impares deben tener órdenes de nodos idénticos. Si no es así, el grupo creará polígonos "estrellados", con elementos superpuestos.

 y
y

 son ordinarios, mientras
son ordinarios, mientras

 Está estrellado.
Está estrellado.
12 grupos de Shephard irreducibles

p [2 q ] 2 → p [ q ] p , índice 2.
p [4] q → p [ q ] p , índice q .
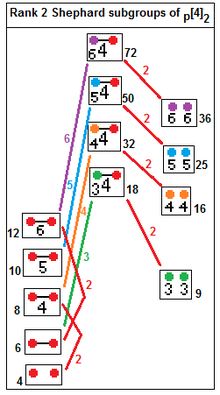
p [4] 2 → [ p ], índice p
p [4] 2 → p []× p [], índice 2
Coxeter enumeró esta lista de polígonos complejos regulares en . Un polígono complejo regular, p { q } r o

 , tiene p -aristas y r -figuras de vértices gonales . p { q } r es un politopo finito si ( p + r ) q > pr ( q -2).
, tiene p -aristas y r -figuras de vértices gonales . p { q } r es un politopo finito si ( p + r ) q > pr ( q -2).
Su simetría se escribe como p [ q ] r , llamado grupo de Shephard , análogo a un grupo de Coxeter , aunque también permite reflexiones unitarias .
Para los grupos no estelares, el orden del grupo p [ q ] r se puede calcular como . [9]
El número de Coxeter para p [ q ] r es , por lo que el orden del grupo también se puede calcular como . Se puede dibujar un polígono complejo regular en proyección ortogonal con simetría h -gonal.
Las soluciones de rango 2 que generan polígonos complejos son:
| Grupo | G3 = G( q ,1,1) | G2 = G( p , 1,2) | G 4 | G 6 | G 5 | G 8 | G 14 | G 9 | G10 | G20 | G 16 | G21 | G 17 | G 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 [ q ] 2 , q =3,4... | p [4] 2 , p =2,3... | 3 [3] 3 | 3 [6] 2 | 3 [4] 3 | 4 [3] 4 | 3 [8] 2 | 4 [6] 2 | 4 [4] 3 | 3 [5] 3 | 5 [3] 5 | 3 [10] 2 | 5 [6] 2 | 5 [4] 3 | |
   |    |    |    |    |    |    |    |    |    |    |    |    |    | |
| Orden | 2 q | 2 pág. 2 | 24 | 48 | 72 | 96 | 144 | 192 | 288 | 360 | 600 | 720 | 1200 | 1800 |
| yo | q | 2 p | 6 | 12 | 24 | 30 | 60 | |||||||
Las soluciones excluidas con q impar y p y r desiguales son: 6 [3] 2 , 6 [3] 3 , 9 [3] 3 , 12 [3] 3 , ..., 5 [5] 2 , 6 [ 5] 2 , 8 [5] 2 , 9 [5] 2 , 4 [7] 2 , 9 [5] 2 , 3 [9] 2 y 3 [11] 2 .
Otros q enteros con p y r desiguales , crean grupos estrellados con dominios fundamentales superpuestos:

 ,
,

 ,
,

 ,
,

 ,
,

 , y
, y

 .
.
El polígono dual de p { q } r es r { q } p . Un polígono de la forma p { q } p es autodual. Los grupos de la forma p [2 q ] 2 tienen una semisimetría p [ q ] p , por lo que un polígono regular




 es lo mismo que cuasirregular
es lo mismo que cuasirregular



 . Además, polígono regular con el mismo orden de nodos,
. Además, polígono regular con el mismo orden de nodos,



 , tienen una construcción alternada
, tienen una construcción alternada




 , permitiendo que los bordes adyacentes sean de dos colores diferentes. [10]
, permitiendo que los bordes adyacentes sean de dos colores diferentes. [10]
El orden de grupo, g , se utiliza para calcular el número total de vértices y aristas. Tendrá g / r vértices y g / p aristas. Cuando p = r , el número de vértices y aristas es igual. Esta condición es necesaria cuando q es impar.
Generadores de matrices
El grupo p [ q ] r ,

 , se puede representar mediante dos matrices: [11]
, se puede representar mediante dos matrices: [11]
| Nombre | R1 | R2 |
|---|---|---|
| Orden | pag | a |
| Matriz |
Con
- k=
- Ejemplos
|
|
| |||||||||||||||||||||||||||
|
|
|
Enumeración de polígonos regulares complejos
Coxeter enumeró los polígonos complejos en la Tabla III de Politopos complejos regulares. [12]
| Grupo | Orden | Número de Coxeter | Polígono | Vértices | Bordes | Notas | ||
|---|---|---|---|---|---|---|---|---|
| G(q,q,2) 2 [ q ] 2 = [ q ] q=2,3,4,... | 2 q | q | 2 { q } 2 |    | q | q | {} | Polígonos regulares reales Igual que     Lo mismo que      si q aun si q aun |
| Grupo | Orden | Número de Coxeter | Polígono | Vértices | Bordes | Notas | |||
|---|---|---|---|---|---|---|---|---|---|
| G( p ,1,2) p [4] 2 p=2,3,4,... | 2 pág. 2 | 2 p | pág. (2 pág. 2 )2 | pág {4} 2 |    | pág. 2 | 2 p | pag {} | lo mismo que p {}× p {} o   Representación como duoprisma p - p |
| 2(2 pág. 2 ) pág. | 2 {4} p |    | 2 p | pág. 2 | {} | Representación como duopirámide p - p | |||
| G(2,1,2) 2 [4] 2 = [4] | 8 | 4 | 2 {4} 2 = {4} |    | 4 | 4 | {} | lo mismo que {}×{} o   Cuadrado real | |
| G(3,1,2) 3 [4] 2 | 18 | 6 | 6(18)2 | 3 {4} 2 |    | 9 | 6 | 3 {} | lo mismo que 3 {}× 3 {} o   Representación como duoprisma 3-3 |
| 2(18)3 | 2 {4} 3 |    | 6 | 9 | {} | Representación como duopirámide 3-3 | |||
| G(4,1,2) 4 [4] 2 | 32 | 8 | 8(32)2 | 4 {4} 2 |    | 16 | 8 | 4 {} | lo mismo que 4 {}× 4 {} o   representación como duoprisma 4-4 o {4,3,3} |
| 2(32)4 | 2 {4} 4 |    | 8 | 16 | {} | Representación como duopirámide 4-4 o {3,3,4} | |||
| G(5,1,2) 5 [4] 2 | 50 | 25 | 5(50)2 | 5 {4} 2 |    | 25 | 10 | 5 {} | lo mismo que 5 {}× 5 {} o   Representación como duoprisma 5-5 |
| 2(50)5 | 2 {4} 5 |    | 10 | 25 | {} | Representación como duopirámide 5-5 | |||
| G(6,1,2) 6 [4] 2 | 72 | 36 | 6(72)2 | 6 {4} 2 |    | 36 | 12 | 6 {} | lo mismo que 6 {}× 6 {} o   Representación como duoprisma 6-6 |
| 2(72)6 | 2 {4} 6 |    | 12 | 36 | {} | Representación como duopirámide 6-6 | |||
| G 4 = G (1, 1, 2) 3 [3] 3 <2, 3, 3> | 24 | 6 | 3(24)3 | 3 {3} 3 |    | 8 | 8 | 3 {} | Configuración autodual de Möbius-Kantor, igual que    representación como {3,3,4} |
| G63 [ 6 ] 2 | 48 | 12 | 3(48)2 | 3 {6} 2 |    | 24 | 16 | 3 {} | Lo mismo que   |
| 3 {3} 2 |    | polígono estrellado | |||||||
| 2(48)3 | 2 {6} 3 |    | 16 | 24 | {} | ||||
| 2 {3} 3 |    | polígono estrellado | |||||||
| G 5 3 [4] 3 | 72 | 12 | 3(72)3 | 3 {4} 3 |    | 24 | 24 | 3 {} | auto-dual, lo mismo que   representación como {3,4,3} |
| G84 [ 3 ] 4 | 96 | 12 | 4(96)4 | 4 {3} 4 |    | 24 | 24 | 4 {} | auto-dual, lo mismo que   representación como {3,4,3} |
| G143 [ 8 ] 2 | 144 | 24 | 3(144)2 | 3 {8} 2 |    | 72 | 48 | 3 {} | Lo mismo que   |
| 3 {8/3} 2 |      | polígono estrellado, lo mismo que     | |||||||
| 2(144)3 | 2 {8} 3 |    | 48 | 72 | {} | ||||
| 2 {8/3} 3 |      | polígono estrellado | |||||||
| G94 [ 6 ] 2 | 192 | 24 | 4(192)2 | 4 {6} 2 |    | 96 | 48 | 4 {} | Lo mismo que   |
| 2(192)4 | 2 {6} 4 |    | 48 | 96 | {} | ||||
| 4 {3} 2 |    | 96 | 48 | {} | polígono estrellado | ||||
| 2 {3} 4 |    | 48 | 96 | {} | polígono estrellado | ||||
| G10 4 [ 4] 3 | 288 | 24 | 4(288)3 | 4 {4} 3 |    | 96 | 72 | 4 {} | |
| 12 | 4 {8/3} 3 |      | polígono estrellado | ||||||
| 24 | 3(288)4 | 3 {4} 4 |    | 72 | 96 | 3 {} | |||
| 12 | 3 {8/3} 4 |      | polígono estrellado | ||||||
| G203 [ 5 ] 3 | 360 | 30 | 3(360)3 | 3 {5} 3 |    | 120 | 120 | 3 {} | auto-dual, lo mismo que   representación como {3,3,5} |
| 3 {5/2} 3 |  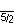  | Polígono estrellado autodual | |||||||
| G16 5 [3 ] 5 | 600 | 30 | 5(600)5 | 5 {3} 5 |    | 120 | 120 | 5 {} | auto-dual, lo mismo que   representación como {3,3,5} |
| 10 | 5 {5/2} 5 |  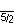  | Polígono estrellado autodual | ||||||
| G213 [ 10 ] 2 | 720 | 60 | 3(720)2 | 3 {10} 2 |    | 360 | 240 | 3 {} | Lo mismo que   |
| 3 {5} 2 |    | polígono estrellado | |||||||
| 3 {10/3} 2 |      | polígono estrellado, lo mismo que     | |||||||
| 3 {5/2} 2 |  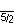  | polígono estrellado | |||||||
| 2(720)3 | 2 {10} 3 |    | 240 | 360 | {} | ||||
| 2 {5} 3 |    | polígono estrellado | |||||||
| 2 {10/3} 3 |      | polígono estrellado | |||||||
| 2 {5/2} 3 |  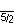  | polígono estrellado | |||||||
| G17 5 [6 ] 2 | 1200 | 60 | 5(1200)2 | 5 {6} 2 |    | 600 | 240 | 5 {} | Lo mismo que   |
| 20 | 5 {5} 2 |    | polígono estrellado | ||||||
| 20 | 5 {10/3} 2 |      | polígono estrellado | ||||||
| 60 | 5 {3} 2 |    | polígono estrellado | ||||||
| 60 | 2(1200)5 | 2 {6} 5 |    | 240 | 600 | {} | |||
| 20 | 2 {5} 5 |    | polígono estrellado | ||||||
| 20 | 2 {10/3} 5 |      | polígono estrellado | ||||||
| 60 | 2 {3} 5 |    | polígono estrellado | ||||||
| G18 5 [4 ] 3 | 1800 | 60 | 5(1800)3 | 5 {4} 3 |    | 600 | 360 | 5 {} | |
| 15 | 5 {10/3} 3 |      | polígono estrellado | ||||||
| 30 | 5 {3} 3 |    | polígono estrellado | ||||||
| 30 | 5 {5/2} 3 |  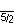  | polígono estrellado | ||||||
| 60 | 3(1800)5 | 3 {4} 5 |    | 360 | 600 | 3 {} | |||
| 15 | 3 {10/3} 5 |      | polígono estrellado | ||||||
| 30 | 3 {3} 5 |    | polígono estrellado | ||||||
| 30 | 3 {5/2} 5 |  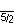  | polígono estrellado | ||||||
Visualizaciones de polígonos regulares complejos
Los polígonos de la forma p {2 r } q se pueden visualizar mediante q conjuntos de colores de p -aristas. Cada p -arista se ve como un polígono regular, aunque no hay caras.
- Proyecciones ortogonales 2D de polígonos complejos 2 { r } q
Los polígonos de la forma 2 {4} q se denominan ortoplexos generalizados . Comparten vértices con las duopirámides 4D q - q , vértices conectados por 2 aristas.
- 2 {4} 2 ,


 , con 4 vértices y 4 aristas
, con 4 vértices y 4 aristas - 2 {4} 3 ,


 , con 6 vértices y 9 aristas [13]
, con 6 vértices y 9 aristas [13] - 2 {4} 4 ,


 , con 8 vértices y 16 aristas
, con 8 vértices y 16 aristas - 2 {4} 5 ,


 , con 10 vértices y 25 aristas
, con 10 vértices y 25 aristas - 2 {4} 6 ,


 , con 12 vértices y 36 aristas
, con 12 vértices y 36 aristas - 2 {4} 7 ,


 , con 14 vértices y 49 aristas
, con 14 vértices y 49 aristas - 2 {4} 8 ,


 , con 16 vértices y 64 aristas
, con 16 vértices y 64 aristas - 2 {4} 9 ,


 , con 18 vértices y 81 aristas
, con 18 vértices y 81 aristas - 2 {4} 10 ,


 , con 20 vértices y 100 aristas
, con 20 vértices y 100 aristas
- Polígonos complejos p {4} 2
Los polígonos de la forma p {4} 2 se denominan hipercubos generalizados (cuadrados para polígonos). Comparten vértices con los duoprismas 4D p - p , vértices conectados por p-aristas. Los vértices se dibujan en verde y las p -aristas se dibujan en colores alternos, rojo y azul. La perspectiva se distorsiona ligeramente para las dimensiones impares para mover los vértices superpuestos desde el centro.
- 2 {4} 2 ,


 o
o

 , con 4 vértices y 4 aristas de 2 caras
, con 4 vértices y 4 aristas de 2 caras - 3 {4} 2 ,


 o
o

 , con 9 vértices y 6 aristas triangulares [13]
, con 9 vértices y 6 aristas triangulares [13] - 4 {4} 2 ,


 o
o

 , con 16 vértices y 8 aristas cuadradas de 4 lados
, con 16 vértices y 8 aristas cuadradas de 4 lados - 5 {4} 2 ,


 o
o

 , con 25 vértices y 10 aristas de 5 lados (pentagonales)
, con 25 vértices y 10 aristas de 5 lados (pentagonales) - 6 {4} 2 ,


 o
o

 , con 36 vértices y 12 aristas (hexagonales) de 6
, con 36 vértices y 12 aristas (hexagonales) de 6 - 7 {4} 2 ,


 o
o

 , con 49 vértices y 14 aristas (heptagonales) de 7 lados
, con 49 vértices y 14 aristas (heptagonales) de 7 lados - 8 {4} 2 ,


 o
o

 , con 64 vértices y 16 aristas de 8 caras (octagonales)
, con 64 vértices y 16 aristas de 8 caras (octagonales) - 9 {4} 2 ,


 o
o

 , con 81 vértices y 18 aristas de 9 lados (aneogonales)
, con 81 vértices y 18 aristas de 9 lados (aneogonales) - 10 {4} 2 ,


 o
o

 , con 100 vértices y 20 aristas de 10 (decagonales)
, con 100 vértices y 20 aristas de 10 (decagonales)
- Proyecciones en perspectiva 3D de polígonos complejos p {4} 2 . Los duales 2 {4} p
- se ven agregando vértices dentro de los bordes y agregando bordes en lugar de vértices.
- 3 {4} 2 ,


 o
o

 con 9 vértices, 6 aristas de 3 lados en 2 conjuntos de colores
con 9 vértices, 6 aristas de 3 lados en 2 conjuntos de colores - 2 {4} 3 ,


 con 6 vértices, 9 aristas en 3 conjuntos
con 6 vértices, 9 aristas en 3 conjuntos - 4 {4} 2 ,


 o
o

 con 16 vértices, 8 de 4 aristas en 2 conjuntos de colores y cuadrado relleno de 4 aristas
con 16 vértices, 8 de 4 aristas en 2 conjuntos de colores y cuadrado relleno de 4 aristas - 5 {4} 2 ,


 o
o

 con 25 vértices, 10 de 5 aristas en 2 conjuntos de colores
con 25 vértices, 10 de 5 aristas en 2 conjuntos de colores
- Otros polígonos complejos p { r } 2
- 3 {6} 2 ,


 o
o

 , con 24 vértices en negro y 16 aristas de 3 colores en 2 conjuntos de aristas de 3 colores en rojo y azul [14]
, con 24 vértices en negro y 16 aristas de 3 colores en 2 conjuntos de aristas de 3 colores en rojo y azul [14] - 3 {8} 2 ,


 o
o

 , con 72 vértices en negro y 48 aristas de 3 colores en 2 conjuntos de aristas de 3 colores en rojo y azul [15]
, con 72 vértices en negro y 48 aristas de 3 colores en 2 conjuntos de aristas de 3 colores en rojo y azul [15]
- Proyecciones ortogonales 2D de polígonos complejos, p { r } p
Los polígonos de la forma p { r } p tienen el mismo número de vértices y aristas. También son autoduales.
- 3 {3} 3 ,


 o
o

 , con 8 vértices en negro y 8 aristas de 3 colores en 2 conjuntos de aristas de 3 colores en rojo y azul [16]
, con 8 vértices en negro y 8 aristas de 3 colores en 2 conjuntos de aristas de 3 colores en rojo y azul [16] - 3 {4} 3 ,


 o
o

 , con 24 vértices y 24 aristas de 3 lados que se muestran en 3 conjuntos de colores, un conjunto lleno [17]
, con 24 vértices y 24 aristas de 3 lados que se muestran en 3 conjuntos de colores, un conjunto lleno [17] - 4 {3} 4 ,


 o
o

 , con 24 vértices y 24 aristas de 4 lados que se muestran en 4 conjuntos de colores [17]
, con 24 vértices y 24 aristas de 4 lados que se muestran en 4 conjuntos de colores [17] - 3 {5} 3 ,


 o
o

 , con 120 vértices y 120 3 aristas [18]
, con 120 vértices y 120 3 aristas [18] - 5 {3} 5 ,


 o
o

 , con 120 vértices y 120 aristas de 5 puntos [19]
, con 120 vértices y 120 aristas de 5 puntos [19]
Politopos complejos regulares
En general, un politopo complejo regular se representa por Coxeter como p { z 1 } q {z 2 } r {z 3 } s ... o diagrama de Coxeter


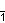











 ..., que tiene simetría p [ z 1 ] q [ z 2 ] r [ z 3 ] s ... o
..., que tiene simetría p [ z 1 ] q [ z 2 ] r [ z 3 ] s ... o


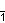











 .... [20]
.... [20]
Existen infinitas familias de politopos complejos regulares que se dan en todas las dimensiones, generalizando los hipercubos y politopos cruzados en el espacio real. El "ortótopo generalizado" de Shephard generaliza el hipercubo; su símbolo es γ.pn
= p {4} 2 {3} 2 ... 2 {3} 2 y diagrama






 ...
...



 Su grupo de simetría tiene el diagrama p [4] 2 [3] 2 ... 2 [3] 2 ; en la clasificación de Shephard–Todd, este es el grupo G( p , 1, n ) que generaliza las matrices de permutación con signo. Su politopo regular dual, el "politopo cruzado generalizado", se representa con el símbolo βpn
Su grupo de simetría tiene el diagrama p [4] 2 [3] 2 ... 2 [3] 2 ; en la clasificación de Shephard–Todd, este es el grupo G( p , 1, n ) que generaliza las matrices de permutación con signo. Su politopo regular dual, el "politopo cruzado generalizado", se representa con el símbolo βpn
= 2 {3} 2 {3} 2 ... 2 {4} p y diagrama






 ...
...


 . [21]
. [21]
Un politopo complejo regular unidimensional se representa como , que tiene p vértices, y su representación real es un polígono regular , { p }. Coxeter también le da el símbolo γpág.
, que tiene p vértices, y su representación real es un polígono regular , { p }. Coxeter también le da el símbolo γpág.
1o βpág.
1como hipercubo generalizado unidimensional o politopo cruzado. Su simetría es p [] o , un grupo cíclico de orden p . En un politopo superior, p {} o
, un grupo cíclico de orden p . En un politopo superior, p {} o representa un elemento de borde p , con un borde 2, {} o
representa un elemento de borde p , con un borde 2, {} o , que representa un borde real ordinario entre dos vértices. [21]
, que representa un borde real ordinario entre dos vértices. [21]
Un politopo complejo dual se construye intercambiando k y ( n -1- k )-elementos de un n -politopo. Por ejemplo, un polígono complejo dual tiene vértices centrados en cada arista, y las nuevas aristas están centradas en los vértices antiguos. Un vértice de v -valencia crea una nueva arista v , y las aristas e se convierten en vértices de e -valencia. [22] El dual de un politopo complejo regular tiene un símbolo invertido. Los politopos complejos regulares con símbolos simétricos, es decir , p { q } p , p { q } r { q } p , p { q } r { s } r { q } p , etc. son autoduales .
Enumeración de poliedros regulares complejos

Coxeter enumeró esta lista de poliedros complejos regulares no estelares en , incluidos los 5 sólidos platónicos en . [23]
Un poliedro complejo regular, p { n 1 } q { n 2 } r o


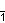






 , tiene
, tiene



 caras,
caras, bordes, y
bordes, y




 figuras de vértice .
figuras de vértice .
Un poliedro regular complejo p { n 1 } q { n 2 } r requiere que tanto g 1 = order( p [ n 1 ] q ) como g 2 = order( q [ n 2 ] r ) sean finitos.
Dado g = orden ( p [ n 1 ] q [ n 2 ] r ), el número de vértices es g / g 2 , y el número de caras es g / g 1 . El número de aristas es g / pr .
| Espacio | Grupo | Orden | Número de Coxeter | Polígono | Vértices | Bordes | Caras | Figura de vértice | Polígono de Van Oss | Notas | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G(1,1,3) 2 [3] 2 [3] 2 = [3,3] | 24 | 4 | α3 = 2 {3} 2 {3} 2 = {3,3 } |      | 4 | 6 | {} | 4 | {3} | {3} | ninguno | Tetraedro real Igual que      | |
| G23 2 [3] 2 [5] 2 = [3,5 ] | 120 | 10 | 2 {3} 2 {5} 2 = {3,5} |      | 12 | 30 | {} | 20 | {3} | {5} | ninguno | Icosaedro real | |
| 2 {5} 2 {3} 2 = {5,3} |      | 20 | 30 | {} | 12 | {5} | {3} | ninguno | Dodecaedro real | ||||
| G(2,1,3) 2 [3] 2 [4] 2 = [3,4] | 48 | 6 | β2 3= β3 = {3,4} |      | 6 | 12 | {} | 8 | {3} | {4} | {4} | Octaedro real Igual que {}+{}+{}, orden 8 Igual que    , orden 24 , orden 24 | |
| gamma2 3= γ3 = {4,3} |      | 8 | 12 | {} | 6 | {4} | {3} | ninguno | Cubo real Igual que {}×{}×{} o      | ||||
| G(p,1,3) 2 [3] 2 [4] p p=2,3,4,... | 6 pág. 3 | 3 p | βpág. 3= 2 {3} 2 {4} p |      | 3 p | 3 pág. 2 | {} | pág. 3 | {3} | 2 {4} p | 2 {4} p | Octaedro generalizado Igual que p {}+ p {}+ p {}, orden p 3 Igual que     , orden 6 p 2 , orden 6 p 2 | |
| gammapág. 3= p {4} 2 {3} 2 |      | pág. 3 | 3 pág. 2 | pag {} | 3 p | pág {4} 2 | {3} | ninguno | Cubo generalizado Igual que p {}× p {}× p {} o      | ||||
| G(3,1,3) 2 [3] 2 [4] 3 | 162 | 9 | β3 3= 2 {3} 2 {4} 3 |      | 9 | 27 | {} | 27 | {3} | 2 {4} 3 | 2 {4} 3 | Igual que 3 {}+ 3 {}+ 3 {}, orden 27 Igual que    , orden 54 , orden 54 | |
| gamma3 3= 3 {4} 2 {3} 2 |      | 27 | 27 | 3 {} | 9 | 3 {4} 2 | {3} | ninguno | Lo mismo que 3 {}× 3 {}× 3 {} o     | ||||
| G(4,1,3) 2 [3] 2 [4] 4 | 384 | 12 | β4 3= 2 {3} 2 {4} 4 |      | 12 | 48 | {} | 64 | {3} | 2 {4} 4 | 2 {4} 4 | Igual que 4 {}+ 4 {}+ 4 {}, orden 64 Igual que     , orden 96 , orden 96 | |
| gamma4 3= 4 {4} 2 {3} 2 |      | 64 | 48 | 4 {} | 12 | 4 {4} 2 | {3} | ninguno | Igual que 4 {}× 4 {}× 4 {} o     | ||||
| G(5,1,3) 2 [3] 2 [4] 5 | 750 | 15 | β5 3= 2 {3} 2 {4} 5 |      | 15 | 75 | {} | 125 | {3} | 2 {4} 5 | 2 {4} 5 | Igual que 5 {}+ 5 {}+ 5 {}, orden 125 Igual que     , orden 150 , orden 150 | |
| gamma5 3= 5 {4} 2 {3} 2 |      | 125 | 75 | 5 {} | 15 | 5 {4} 2 | {3} | ninguno | Lo mismo que 5 {}× 5 {}× 5 {} o     | ||||
| G(6,1,3) 2 [3] 2 [4] 6 | 1296 | 18 | β6 3= 2 {3} 2 {4} 6 |      | 36 | 108 | {} | 216 | {3} | 2 {4} 6 | 2 {4} 6 | Igual que 6 {}+ 6 {}+ 6 {}, orden 216 Igual que     , orden 216 , orden 216 | |
| gamma6 3= 6 {4} 2 {3} 2 |      | 216 | 108 | 6 {} | 18 | 6 {4} 2 | {3} | ninguno | Igual que 6 {}× 6 {}× 6 {} o     | ||||
| G25 3 [ 3] 3 [3] 3 | 648 | 9 | 3 {3} 3 {3} 3 |      | 27 | 72 | 3 {} | 27 | 3 {3} 3 | 3 {3} 3 | 3 {4} 2 | Lo mismo que     . representación como poliedro de Hesse 2 21 . representación como poliedro de Hesse 2 21 | |
| G26 2 [ 4] 3 [3] 3 | 1296 | 18 | 2 {4} 3 {3} 3 |      | 54 | 216 | {} | 72 | 2 {4} 3 | 3 {3} 3 | {6} | ||
| 3 {3} 3 {4} 2 |      | 72 | 216 | 3 {} | 54 | 3 {3} 3 | 3 {4} 2 | 3 {4} 3 | Lo mismo que     [24] representación como 1 22 [24] representación como 1 22 | ||||
Visualizaciones de poliedros complejos regulares
- Proyecciones ortogonales 2D de poliedros complejos, p { s } t { r } r
- 3 {3} 3 {3} 3 ,




 o
o



 , tiene 27 vértices, 72 aristas triples y 27 caras, con una cara resaltada en azul. [25]
, tiene 27 vértices, 72 aristas triples y 27 caras, con una cara resaltada en azul. [25] - 2 {4} 3 {3} 3 ,




 tiene 54 vértices, 216 aristas simples y 72 caras, con una cara resaltada en azul. [26]
tiene 54 vértices, 216 aristas simples y 72 caras, con una cara resaltada en azul. [26] - 3 {3} 3 {4} 2 ,




 o
o



 , tiene 72 vértices, 216 3 aristas y 54 vértices, con una cara resaltada en azul. [27]
, tiene 72 vértices, 216 3 aristas y 54 vértices, con una cara resaltada en azul. [27]
- Octaedros generalizados
Los octaedros generalizados tienen una construcción regular como



 y forma cuasirregular como
y forma cuasirregular como


 . Todos los elementos son símplex .
. Todos los elementos son símplex .
- 2 {3} 2 {4} 3 ,




 o
o

 , con 9 vértices, 27 aristas y 27 caras
, con 9 vértices, 27 aristas y 27 caras - 2 {3} 2 {4} 4 ,




 o
o


 , con 12 vértices, 48 aristas y 64 caras
, con 12 vértices, 48 aristas y 64 caras - 2 {3} 2 {4} 5 ,




 o
o


 , con 15 vértices, 75 aristas y 125 caras
, con 15 vértices, 75 aristas y 125 caras - 2 {3} 2 {4} 6 ,




 o
o


 , con 18 vértices, 108 aristas y 216 caras
, con 18 vértices, 108 aristas y 216 caras - 2 {3} 2 {4} 7 ,




 o
o


 , con 21 vértices, 147 aristas y 343 caras
, con 21 vértices, 147 aristas y 343 caras - 2 {3} 2 {4} 8 ,




 o
o


 , con 24 vértices, 192 aristas y 512 caras
, con 24 vértices, 192 aristas y 512 caras - 2 {3} 2 {4} 9 ,




 o
o


 , con 27 vértices, 243 aristas y 729 caras
, con 27 vértices, 243 aristas y 729 caras - 2 {3} 2 {4} 10 ,




 o
o



 , con 30 vértices, 300 aristas y 1000 caras
, con 30 vértices, 300 aristas y 1000 caras
- Cubos generalizados
Los cubos generalizados tienen una construcción regular como



 y construcción prismática como
y construcción prismática como



 , un producto de tres 1-politopos p -gonales. Los elementos son cubos generalizados de menor dimensión.
, un producto de tres 1-politopos p -gonales. Los elementos son cubos generalizados de menor dimensión.
- 3 {4} 2 {3} 2 ,




 o
o



 tiene 27 vértices, 27 aristas triples y 9 caras [25]
tiene 27 vértices, 27 aristas triples y 9 caras [25] - 4 {4} 2 {3} 2 ,




 o
o



 , con 64 vértices, 48 aristas y 12 caras
, con 64 vértices, 48 aristas y 12 caras - 5 {4} 2 {3} 2 ,




 o
o



 , con 125 vértices, 75 aristas y 15 caras
, con 125 vértices, 75 aristas y 15 caras - 6 {4} 2 {3} 2 ,




 o
o



 , con 216 vértices, 108 aristas y 18 caras
, con 216 vértices, 108 aristas y 18 caras - 7 {4} 2 {3} 2 ,




 o
o



 , con 343 vértices, 147 aristas y 21 caras
, con 343 vértices, 147 aristas y 21 caras - 8 {4} 2 {3} 2 ,




 o
o



 , con 512 vértices, 192 aristas y 24 caras
, con 512 vértices, 192 aristas y 24 caras - 9 {4} 2 {3} 2 ,




 o
o



 , con 729 vértices, 243 aristas y 27 caras
, con 729 vértices, 243 aristas y 27 caras - 10 {4} 2 {3} 2 ,




 o
o



 , con 1000 vértices, 300 aristas y 30 caras
, con 1000 vértices, 300 aristas y 30 caras
Enumeración de 4-politopos complejos regulares
Coxeter enumeró esta lista de 4-politopos complejos regulares no estelares en , incluidos los 6 4-politopos regulares convexos en . [23]
| Espacio | Grupo | Orden | Número de Coxeter | Politopo | Vértices | Bordes | Caras | Células | Polígono de Van Oss | Notas |
|---|---|---|---|---|---|---|---|---|---|---|
| G(1,1,4) 2 [3] 2 [3] 2 [3] 2 = [3,3,3] | 120 | 5 | α4 = 2 {3} 2 {3} 2 {3} 2 = {3,3,3 }       | 5 | 10 {} | 10 {3} | 5 {3,3} | ninguno | 5 celdas reales (simplex) | |
| G 28 2 [3] 2 [4] 2 [3] 2 = [3,4,3] | 1152 | 12 | 2 {3} 2 {4} 2 {3} 2 = {3,4,3}       | 24 | 96 {} | 96 {3} | 24 {3,4} | {6} | Real de 24 celdas | |
| G 30 2 [3] 2 [3] 2 [5] 2 = [3,3,5] | 14400 | 30 | 2 {3} 2 {3} 2 {5} 2 = {3,3,5}       | 120 | 720 {} | 1200 {3} | 600 {3,3} | {10} | 600 celdas reales | |
2 {5} 2 {3} 2 {3} 2 = {5,3,3}       | 600 | 1200 {} | 720 {5} | 120 {5,3} | 120 celdas reales | |||||
| G(2,1,4) 2 [3] 2 [3] 2 [4] p = [3,3,4] | 384 | 8 | β2 4= β 4 = {3,3,4}        | 8 | 24 {} | 32 {3} | 16 {3,3} | {4} | Real 16 celdas Igual que      , orden 192 , orden 192 | |
| gamma2 4= γ 4 = {4,3,3}        | 16 | 32 {} | 24 {4} | 8 {4,3} | ninguno | Teseracto real Igual que {} 4 o        , orden 16 , orden 16 | ||||
| G(p,1,4) 2 [3] 2 [3] 2 [4] p p=2,3,4,... | 24 pág. 4 | 4 p | βpág. 4= 2 {3} 2 {3} 2 {4}        | 4 p | 6 pág. 2 {} | 4 pág. 3 {3} | pág. 4 {3,3} | 2 {4} p | Ortoplex 4 generalizado Igual que       , pedido 24 p 3 , pedido 24 p 3 | |
| gammapág. 4= p {4} 2 {3} 2 {3} 2        | pág. 4 | 4p3p { } | 6p2p {4} 2 | 4 págs {4} 2 {3} 2 | ninguno | Teseracto generalizado Igual que p {} 4 o        , orden p 4 , orden p 4 | ||||
| G(3,1,4) 2 [3] 2 [3] 2 [4] 3 | 1944 | 12 | β3 4= 2 {3} 2 {3} 2 {4} 3        | 12 | 54 {} | 108 {3} | 81 {3,3} | 2 {4} 3 | Ortoplex 4 generalizado Igual que      , orden 648 , orden 648 | |
| gamma3 4= 3 {4} 2 {3} 2 {3} 2        | 81 | 108 3 {} | 54 3 {4} 2 | 12 3 {4} 2 {3} 2 | ninguno | Lo mismo que 3 {} 4 o       , orden 81 , orden 81 | ||||
| G(4,1,4) 2 [3] 2 [3] 2 [4] 4 | 6144 | 16 | β4 4= 2 {3} 2 {3} 2 {4} 4        | 16 | 96 {} | 256 {3} | 64 {3,3} | 2 {4} 4 | Lo mismo que      , orden 1536 , orden 1536 | |
| gamma4 4= 4 {4} 2 {3} 2 {3} 2        | 256 | 256 4 {} | 96 4 {4} 2 | 16 4 {4} 2 {3} 2 | ninguno | Lo mismo que 4 {} 4 o       , orden 256 , orden 256 | ||||
| G(5,1,4) 2 [3] 2 [3] 2 [4] 5 | 15000 | 20 | β5 4= 2 {3} 2 {3} 2 {4} 5        | 20 | 150 {} | 500 {3} | 625 {3,3} | 2 {4} 5 | Lo mismo que      , orden 3000 , orden 3000 | |
| gamma5 4= 5 {4} 2 {3} 2 {3} 2        | 625 | 500 5 {} | 150 5 {4} 2 | 20 5 {4} 2 {3} 2 | ninguno | Lo mismo que 5 {} 4 o       , orden 625 , orden 625 | ||||
| G(6,1,4) 2 [3] 2 [3] 2 [4] 6 | 31104 | 24 | β6 4= 2 {3} 2 {3} 2 {4} 6        | 24 | 216 {} | 864 {3} | 1296 {3,3} | 2 {4} 6 | Lo mismo que      , orden 5184 , orden 5184 | |
| gamma6 4= 6 {4} 2 {3} 2 {3} 2        | 1296 | 864 6 {} | 216 6 {4} 2 | 24 6 {4} 2 {3} 2 | ninguno | Lo mismo que 6 {} 4 o       , orden 1296 , orden 1296 | ||||
| G32 3 [ 3] 3 [3] 3 [3] 3 | 155520 | 30 | 3 {3} 3 {3} 3 {3} 3        | 240 | 2160 3 {} | 2160 3 {3} 3 | 240 3 {3} 3 {3} 3 | 3 {4} 3 | Representación politópica de Witting como 4 21 |
Visualizaciones de 4-politopos complejos regulares
- Verdadero {3,3,3} ,






 , tenía 5 vértices, 10 aristas, 10 {3} caras y 5 {3,3} celdas
, tenía 5 vértices, 10 aristas, 10 {3} caras y 5 {3,3} celdas - Real {3,4,3} ,






 , tenía 24 vértices, 96 aristas, 96 {3} caras y 24 {3,4} celdas
, tenía 24 vértices, 96 aristas, 96 {3} caras y 24 {3,4} celdas - Real {5,3,3} ,






 , tenía 600 vértices, 1200 aristas, 720 {5} caras y 120 {5,3} celdas
, tenía 600 vértices, 1200 aristas, 720 {5} caras y 120 {5,3} celdas - Real {3,3,5} ,






 , tenía 120 vértices, 720 aristas, 1200 {3} caras y 600 {3,3} celdas
, tenía 120 vértices, 720 aristas, 1200 {3} caras y 600 {3,3} celdas - Politopo ingenioso ,






 , tiene 240 vértices, 2160 3 aristas, 2160 3{3}3 caras y 240 3{3}3{3}3 celdas
, tiene 240 vértices, 2160 3 aristas, 2160 3{3}3 caras y 240 3{3}3{3}3 celdas
- 4-ortoplexes generalizados
Los 4-ortoplex generalizados tienen una construcción regular como





 y forma cuasirregular como
y forma cuasirregular como




 . Todos los elementos son símplex .
. Todos los elementos son símplex .
- 2 {3} 2 {3} 2 {4} 3 ,






 o
o



 , con 12 vértices, 54 aristas, 108 caras y 81 celdas
, con 12 vértices, 54 aristas, 108 caras y 81 celdas - 2 {3} 2 {3} 2 {4} 4 ,






 o
o




 , con 16 vértices, 96 aristas, 256 caras y 256 celdas
, con 16 vértices, 96 aristas, 256 caras y 256 celdas - 2 {3} 2 {3} 2 {4} 5 ,






 o
o




 , con 20 vértices, 150 aristas, 500 caras y 625 celdas
, con 20 vértices, 150 aristas, 500 caras y 625 celdas - 2 {3} 2 {3} 2 {4} 6 ,






 o
o




 , con 24 vértices, 216 aristas, 864 caras y 1296 celdas
, con 24 vértices, 216 aristas, 864 caras y 1296 celdas - 2 {3} 2 {3} 2 {4} 7 ,






 o
o




 , con 28 vértices, 294 aristas, 1372 caras y 2401 celdas
, con 28 vértices, 294 aristas, 1372 caras y 2401 celdas - 2 {3} 2 {3} 2 {4} 8 ,






 o
o




 , con 32 vértices, 384 aristas, 2048 caras y 4096 celdas
, con 32 vértices, 384 aristas, 2048 caras y 4096 celdas - 2 {3} 2 {3} 2 {4} 9 ,






 o
o




 , con 36 vértices, 486 aristas, 2916 caras y 6561 celdas
, con 36 vértices, 486 aristas, 2916 caras y 6561 celdas - 2 {3} 2 {3} 2 {4} 10 ,






 o
o





 , con 40 vértices, 600 aristas, 4000 caras y 10000 celdas
, con 40 vértices, 600 aristas, 4000 caras y 10000 celdas
- 4 cubos generalizados
Los teseractos generalizados tienen una construcción regular como





 y construcción prismática como
y construcción prismática como





 , un producto de cuatro 1-politopos p- gonales. Los elementos son cubos generalizados de menor dimensión.
, un producto de cuatro 1-politopos p- gonales. Los elementos son cubos generalizados de menor dimensión.
- 3 {4} 2 {3} 2 {3} 2 ,






 o
o





 , con 81 vértices, 108 aristas, 54 caras y 12 celdas
, con 81 vértices, 108 aristas, 54 caras y 12 celdas - 4 {4} 2 {3} 2 {3} 2 ,






 o
o





 , con 256 vértices, 96 aristas, 96 caras y 16 celdas
, con 256 vértices, 96 aristas, 96 caras y 16 celdas - 5 {4} 2 {3} 2 {3} 2 ,






 o
o





 , con 625 vértices, 500 aristas, 150 caras y 20 celdas
, con 625 vértices, 500 aristas, 150 caras y 20 celdas - 6 {4} 2 {3} 2 {3} 2 ,






 o
o





 , con 1296 vértices, 864 aristas, 216 caras y 24 celdas
, con 1296 vértices, 864 aristas, 216 caras y 24 celdas - 7 {4} 2 {3} 2 {3} 2 ,






 o
o





 , con 2401 vértices, 1372 aristas, 294 caras y 28 celdas
, con 2401 vértices, 1372 aristas, 294 caras y 28 celdas - 8 {4} 2 {3} 2 {3} 2 ,






 o
o





 , con 4096 vértices, 2048 aristas, 384 caras y 32 celdas
, con 4096 vértices, 2048 aristas, 384 caras y 32 celdas - 9 {4} 2 {3} 2 {3} 2 ,






 o
o





 , con 6561 vértices, 2916 aristas, 486 caras y 36 celdas
, con 6561 vértices, 2916 aristas, 486 caras y 36 celdas - 10 {4} 2 {3} 2 {3} 2 ,






 o
o





 , con 10000 vértices, 4000 aristas, 600 caras y 40 celdas
, con 10000 vértices, 4000 aristas, 600 caras y 40 celdas
Enumeración de 5-politopos complejos regulares
Los politopos complejos regulares de 5 o más dígitos existen en tres familias: los símplex reales y los hipercubos generalizados y ortoplex .
| Espacio | Grupo | Orden | Politopo | Vértices | Bordes | Caras | Células | 4 caras | Polígono de Van Oss | Notas |
|---|---|---|---|---|---|---|---|---|---|---|
| G(1,1,5) = [3,3,3,3] | 720 | α 5 = {3,3,3,3}         | 6 | 15 {} | 20 {3} | 15 {3,3} | 6 {3,3,3} | ninguno | 5-símplex real | |
| G(2,1,5) =[3,3,3,4] | 3840 | β2 5= β 5 = {3,3,3,4}          | 10 | 40 {} | 80 {3} | 80 {3,3} | 32 {3,3,3} | {4} | Ortoplex 5 real Igual que        , orden 1920 , orden 1920 | |
| gamma2 5= γ 5 = {4,3,3,3}          | 32 | 80 {} | 80 {4} | 40 {4,3} | 10 {4,3,3} | ninguno | Cubo 5 real Lo mismo que {} 5 o          , orden 32 , orden 32 | |||
| G(p,1,5) 2 [3] 2 [3] 2 [3] 2 [4] p | 120 pág. 5 | βpág. 5= 2 {3} 2 {3} 2 {3} 2 {4}          | 5 p | 10 pág. 2 {} | 10 pág. 3 {3} | 5 pág. 4 {3,3} | pág. 5 {3,3,3} | 2 {4} p | Ortoplex 5 generalizado Igual que         , pedido 120 p 4 , pedido 120 p 4 | |
| gammapág. 5= p {4} 2 {3} 2 {3} 2 {3} 2          | pág. 5 | 5p4p { } | 10 pág. 3 pág. {4} 2 | 10 pág. 2 pág. {4} 2 {3} 2 | 5 págs {4} 2 {3} 2 {3} 2 | ninguno | 5-cubo generalizado Igual que p {} 5 o          , orden p 5 , orden p 5 | |||
| G(3,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 3 | 29160 | β3 5= 2 {3} 2 {3} 2 {3} 2 {4} 3          | 15 | 90 {} | 270 {3} | 405 {3,3} | 243 {3,3,3} | 2 {4} 3 | Lo mismo que       , orden 9720 , orden 9720 | |
| gamma3 5= 3 {4} 2 {3} 2 {3} 2 {3} 2          | 243 | 405 3 {} | 270 3 {4} 2 | 90 3 {4} 2 {3} 2 | 15 3 {4} 2 {3} 2 {3} 2 | ninguno | Lo mismo que 3 {} 5 o         , orden 243 , orden 243 | |||
| G(4,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 4 | 122880 | β4 5= 2 {3} 2 {3} 2 {3} 2 {4} 4          | 20 | 160 {} | 640 {3} | 1280 {3,3} | 1024 {3,3,3} | 2 {4} 4 | Lo mismo que        , orden 30720 , orden 30720 | |
| gamma4 5= 4 {4} 2 {3} 2 {3} 2 {3} 2          | 1024 | 1280 4 {} | 640 4 {4} 2 | 160 4 {4} 2 {3} 2 | 20 4 {4} 2 {3} 2 {3} 2 | ninguno | Lo mismo que 4 {} 5 o         , orden 1024 , orden 1024 | |||
| G(5,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 5 | 375000 | β5 5= 2 {3} 2 {3} 2 {3} 2 {5} 5          | 25 | 250 {} | 1250 {3} | 3125 {3,3} | 3125 {3,3,3} | 2 {5} 5 | Lo mismo que        , pedido 75000 , pedido 75000 | |
| gamma5 5= 5 {4} 2 {3} 2 {3} 2 {3} 2          | 3125 | 3125 5 {} | 1250 5 {5} 2 | 250 5 {5} 2 {3} 2 | 25 5 {4} 2 {3} 2 {3} 2 | ninguno | Lo mismo que 5 {} 5 o         , orden 3125 , orden 3125 | |||
| G(6,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 6 | 933210 | β6 5= 2 {3} 2 {3} 2 {3} 2 {4} 6          | 30 | 360 {} | 2160 {3} | 6480 {3,3} | 7776 {3,3,3} | 2 {4} 6 | Lo mismo que        , orden 155520 , orden 155520 | |
| gamma6 5= 6 {4} 2 {3} 2 {3} 2 {3} 2          | 7776 | 6480 6 {} | 2160 6 {4} 2 | 360 6 {4} 2 {3} 2 | 30 6 {4} 2 {3} 2 {3} 2 | ninguno | Lo mismo que 6 {} 5 o         , orden 7776 , orden 7776 |
Visualizaciones de 5-politopos complejos regulares
- 5-ortoplexes generalizados
Los 5-ortoplexes generalizados tienen una construcción regular como







 y forma cuasirregular como
y forma cuasirregular como






 . Todos los elementos son símplex .
. Todos los elementos son símplex .
- Verdadero {3,3,3,4} ,








 , con 10 vértices, 40 aristas, 80 caras, 80 celdas y 32 4 caras
, con 10 vértices, 40 aristas, 80 caras, 80 celdas y 32 4 caras - 2 {3} 2 {3} 2 {3} 2 {4} 3 ,








 , con 15 vértices, 90 aristas, 270 caras, 405 celdas y 243 4 caras
, con 15 vértices, 90 aristas, 270 caras, 405 celdas y 243 4 caras - 2 {3} 2 {3} 2 {3} 2 {4} 4 ,








 , con 20 vértices, 160 aristas, 640 caras, 1280 celdas y 1024 4 caras
, con 20 vértices, 160 aristas, 640 caras, 1280 celdas y 1024 4 caras - 2 {3} 2 {3} 2 {3} 2 {4} 5 ,








 , con 25 vértices, 250 aristas, 1250 caras, 3125 celdas y 3125 4 caras
, con 25 vértices, 250 aristas, 1250 caras, 3125 celdas y 3125 4 caras - 2 {3} 2 {3} 2 {3} 2 {4} 6 ,








 , con 30 vértices, 360 aristas, 2160 caras, 6480 celdas, 7776 4 caras
, con 30 vértices, 360 aristas, 2160 caras, 6480 celdas, 7776 4 caras - 2 {3} 2 {3} 2 {3} 2 {4} 7 ,








 , con 35 vértices, 490 aristas, 3430 caras, 12005 celdas, 16807 4 caras
, con 35 vértices, 490 aristas, 3430 caras, 12005 celdas, 16807 4 caras - 2 {3} 2 {3} 2 {3} 2 {4} 8 ,








 , con 40 vértices, 640 aristas, 5120 caras, 20480 celdas, 32768 4 caras
, con 40 vértices, 640 aristas, 5120 caras, 20480 celdas, 32768 4 caras - 2 {3} 2 {3} 2 {3} 2 {4} 9 ,








 , con 45 vértices, 810 aristas, 7290 caras, 32805 celdas, 59049 4 caras
, con 45 vértices, 810 aristas, 7290 caras, 32805 celdas, 59049 4 caras - 2 {3} 2 {3} 2 {3} 2 {4} 10 ,








 , con 50 vértices, 1000 aristas, 10000 caras, 50000 celdas, 100000 4 caras
, con 50 vértices, 1000 aristas, 10000 caras, 50000 celdas, 100000 4 caras
- 5 cubos generalizados
Los 5-cubos generalizados tienen una construcción regular como







 y construcción prismática como
y construcción prismática como







 , un producto de cinco 1-politopos p- gonales. Los elementos son cubos generalizados de menor dimensión.
, un producto de cinco 1-politopos p- gonales. Los elementos son cubos generalizados de menor dimensión.
- Verdadero {4,3,3,3} ,








 , con 32 vértices, 80 aristas, 80 caras, 40 celdas y 10 de 4 caras
, con 32 vértices, 80 aristas, 80 caras, 40 celdas y 10 de 4 caras - 3 {4} 2 {3} 2 {3} 2 {3} 2 ,








 , con 243 vértices, 405 aristas, 270 caras, 90 celdas y 15 de 4 caras
, con 243 vértices, 405 aristas, 270 caras, 90 celdas y 15 de 4 caras - 4 {4} 2 {3} 2 {3} 2 {3} 2 ,








 , con 1024 vértices, 1280 aristas, 640 caras, 160 celdas y 20 de 4 caras
, con 1024 vértices, 1280 aristas, 640 caras, 160 celdas y 20 de 4 caras - 5 {4} 2 {3} 2 {3} 2 {3} 2 ,








 , con 3125 vértices, 3125 aristas, 1250 caras, 250 celdas y 25 4 caras
, con 3125 vértices, 3125 aristas, 1250 caras, 250 celdas y 25 4 caras - 6 {4} 2 {3} 2 {3} 2 {3} 2 ,








 , con 7776 vértices, 6480 aristas, 2160 caras, 360 celdas y 30 de 4 caras
, con 7776 vértices, 6480 aristas, 2160 caras, 360 celdas y 30 de 4 caras
Enumeración de 6-politopos complejos regulares
| Espacio | Grupo | Orden | Politopo | Vértices | Bordes | Caras | Células | 4 caras | 5 caras | Polígono de Van Oss | Notas |
|---|---|---|---|---|---|---|---|---|---|---|---|
| G(1,1,6) = [3,3,3,3,3] | 720 | α 6 = {3,3,3,3,3}           | 7 | 21 {} | 35 {3} | 35 {3,3} | 21 {3,3,3} | 7 {3,3,3,3} | ninguno | 6-símplex real | |
| G(2,1,6) [3,3,3,4] | 46080 | β2 6= β 6 = {3,3,3,4}          | 12 | 60 {} | 160 {3} | 240 {3,3} | 192 {3,3,3} | 64 {3,3,3,3} | {4} | Ortoplex 6 real Igual que          , orden 23040 , orden 23040 | |
| gamma2 6= γ 6 = {4,3,3,3}          | 64 | 192 {} | 240 {4} | 160 {4,3} | 60 {4,3,3} | 12 {4,3,3,3} | ninguno | Cubo real de 6 Lo mismo que {} 6 o            , orden 64 , orden 64 | |||
| G(p,1,6) 2 [3] 2 [3] 2 [3] 2 [4] p | 720 pág. 6 | βpág. 6= 2 {3} 2 {3} 2 {3} 2 {4}          | 6 p | 15 pág. 2 {} | 20 pág. 3 {3} | 15 pág. 4 {3,3} | 6 pág. 5 {3,3,3} | pág. 6 {3,3,3,3} | 2 {4} p | Ortoplex 6 generalizado Igual que           , orden 720 p 5 , orden 720 p 5 | |
| gammapág. 6= p {4} 2 {3} 2 {3} 2 {3} 2          | pág. 6 | 6p5p { } | 15 pág. 4 pág. {4} 2 | 20 pág. 3 pág. {4} 2 {3} 2 | 15 pág. 2 pág. {4} 2 {3} 2 {3} 2 | 6 págs {4} 2 {3} 2 {3} 2 {3} 2 | ninguno | Cubo 6 generalizado Igual que p {} 6 o            , orden p 6 , orden p 6 |
Visualizaciones de 6-politopos complejos regulares
- 6-ortoplexes generalizados
Los 6-ortoplexes generalizados tienen una construcción regular como









 y forma cuasirregular como
y forma cuasirregular como








 . Todos los elementos son símplex .
. Todos los elementos son símplex .
- Verdadero {3,3,3,3,4} ,










 , con 12 vértices, 60 aristas, 160 caras, 240 celdas, 192 de 4 caras y 64 de 5 caras
, con 12 vértices, 60 aristas, 160 caras, 240 celdas, 192 de 4 caras y 64 de 5 caras - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 3 ,










 , con 18 vértices, 135 aristas, 540 caras, 1215 celdas, 1458 de 4 caras y 729 de 5 caras
, con 18 vértices, 135 aristas, 540 caras, 1215 celdas, 1458 de 4 caras y 729 de 5 caras - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 4 ,










 , con 24 vértices, 240 aristas, 1280 caras, 3840 celdas, 6144 de 4 caras y 4096 de 5 caras
, con 24 vértices, 240 aristas, 1280 caras, 3840 celdas, 6144 de 4 caras y 4096 de 5 caras - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 5 ,










 , con 30 vértices, 375 aristas, 2500 caras, 9375 celdas, 18750 de 4 caras y 15625 de 5 caras
, con 30 vértices, 375 aristas, 2500 caras, 9375 celdas, 18750 de 4 caras y 15625 de 5 caras - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 6 ,










 , con 36 vértices, 540 aristas, 4320 caras, 19440 celdas, 46656 de 4 caras y 46656 de 5 caras
, con 36 vértices, 540 aristas, 4320 caras, 19440 celdas, 46656 de 4 caras y 46656 de 5 caras - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 7 ,










 , con 42 vértices, 735 aristas, 6860 caras, 36015 celdas, 100842 4-caras, 117649 5-caras
, con 42 vértices, 735 aristas, 6860 caras, 36015 celdas, 100842 4-caras, 117649 5-caras - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 8 ,










 , con 48 vértices, 960 aristas, 10240 caras, 61440 celdas, 196608 4 caras, 262144 5 caras
, con 48 vértices, 960 aristas, 10240 caras, 61440 celdas, 196608 4 caras, 262144 5 caras - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 9 ,










 , con 54 vértices, 1215 aristas, 14580 caras, 98415 celdas, 354294 4-caras, 531441 5-caras
, con 54 vértices, 1215 aristas, 14580 caras, 98415 celdas, 354294 4-caras, 531441 5-caras - 2 {3} 2 {3} 2 {3} 2 {3} 2 {4} 10 ,










 , con 60 vértices, 1500 aristas, 20000 caras, 150000 celdas, 600000 de 4 caras, 1000000 de 5 caras
, con 60 vértices, 1500 aristas, 20000 caras, 150000 celdas, 600000 de 4 caras, 1000000 de 5 caras
- 6 cubos generalizados
Los 6 cubos generalizados tienen una construcción regular como









 y construcción prismática como
y construcción prismática como









 , un producto de seis 1-politopos p- gonales. Los elementos son cubos generalizados de menor dimensión.
, un producto de seis 1-politopos p- gonales. Los elementos son cubos generalizados de menor dimensión.
- Verdadero {3,3,3,3,3,4} ,










 , con 64 vértices, 192 aristas, 240 caras, 160 celdas, 60 de 4 caras y 12 de 5 caras
, con 64 vértices, 192 aristas, 240 caras, 160 celdas, 60 de 4 caras y 12 de 5 caras - 3 {4} 2 {3} 2 {3} 2 {3} 2 {3} 2 ,










 , con 729 vértices, 1458 aristas, 1215 caras, 540 celdas, 135 de 4 caras y 18 de 5 caras
, con 729 vértices, 1458 aristas, 1215 caras, 540 celdas, 135 de 4 caras y 18 de 5 caras - 4 {4} 2 {3} 2 {3} 2 {3} 2 {3} 2 ,










 , con 4096 vértices, 6144 aristas, 3840 caras, 1280 celdas, 240 de 4 caras y 24 de 5 caras
, con 4096 vértices, 6144 aristas, 3840 caras, 1280 celdas, 240 de 4 caras y 24 de 5 caras - 5 {4} 2 {3} 2 {3} 2 {3} 2 {3} 2 ,










 , con 15625 vértices, 18750 aristas, 9375 caras, 2500 celdas, 375 de 4 caras y 30 de 5 caras
, con 15625 vértices, 18750 aristas, 9375 caras, 2500 celdas, 375 de 4 caras y 30 de 5 caras
Enumeración de aperiótopos complejos regulares
Coxeter enumeró esta lista de apeirótopos o panales complejos regulares no estelares. [28]
Para cada dimensión hay 12 apeirótopos simbolizados como δp , rn
+1existe en cualquier dimensión , o si p = q = 2. Coxeter los llama panales cúbicos generalizados para n > 2. [29]
Cada uno tiene recuentos de elementos proporcionales dados como:
- k-caras = , donde y n ! denota el factorial de n .
1-politopos complejos regulares
El único 1-politopo complejo regular es ∞ {}, o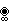 Su representación real es un apeirógono , {∞}, o
Su representación real es un apeirógono , {∞}, o

 .
.
Apeirogonos complejos regulares





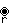 es una mezcla de dos apeirógonos regulares
es una mezcla de dos apeirógonos regulares

 y
y

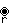 , visto aquí con bordes azules y rosas.
, visto aquí con bordes azules y rosas.

 tiene un solo color de bordes porque q es impar, lo que lo convierte en una cubierta doble.
tiene un solo color de bordes porque q es impar, lo que lo convierte en una cubierta doble.Los apeirógonos complejos de rango 2 tienen simetría p [ q ] r , donde 1/ p + 2/ q + 1/ r = 1. Coxeter los expresa como δp , r
2donde q está restringido a satisfacer q = 2/(1 – ( p + r )/ pr ) . [30]
Hay 8 soluciones:
| 2 [∞] 2 | 3 [12] 2 | 4 [8] 2 | 6 [6] 2 | 3 [6] 3 | 6 [4] 3 | 4 [4] 4 | 6 [3] 6 |
   |    |    |    |    |    |    |    |
Hay dos soluciones excluidas, q impar y p y r desiguales : 10 [5] 2 y 12 [3] 4 , o 

 y
y 

 .
.
Un apeirógono complejo regular p { q } r tiene p -aristas y figuras de vértices r -gonales. El apeirógono dual de p { q } r es r { q } p . Un apeirógono de la forma p { q } p es autodual. Los grupos de la forma p [2 q ] 2 tienen una semisimetría p [ q ] p , por lo que un apeirógono regular


 es lo mismo que cuasirregular
es lo mismo que cuasirregular

 . [31]
. [31]
Los apeirógonos se pueden representar en el plano de Argand y comparten cuatro disposiciones de vértices diferentes. Los apeirógonos de la forma 2 { q } r tienen una disposición de vértices como { q /2, p }. La forma p { q } 2 tiene una disposición de vértices como r{ p , q /2}. Los apeirógonos de la forma p {4} r tienen disposiciones de vértices { p , r }.
Incluyendo nodos afines, y , hay 3 soluciones infinitas más: ∞ [2] ∞ , ∞ [4] 2 , ∞ [3] 3 , y

 ,
,

 , y
, y

 El primero es un subgrupo de índice 2 del segundo. Los vértices de estos apeirógonos existen en .
El primero es un subgrupo de índice 2 del segundo. Los vértices de estos apeirógonos existen en .
| Espacio | Grupo | Apeirogon | Borde | representante [32] | Imagen | Notas | |
|---|---|---|---|---|---|---|---|
| 2 [∞] 2 = [∞] | del2,2 2= {∞} |    | {} |  | Apeirogon real Lo mismo que    | ||
| / | ∞ [4] 2 | ∞ {4} 2 | 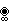   | ∞ {} | {4,4} |  | Lo mismo que    |
| ∞ [3] 3 | ∞ {3} 3 | 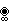   | ∞ {} | {3,6} |  | Lo mismo que     | |
| p [ q ] r | delp,r 2= p { q } r |    | pag {} | ||||
| 3 [12] 2 | del3,2 2= 3 {12} 2 |    | 3 {} | r{3,6} |  | Lo mismo que    | |
| del2,3 2= 2 {12} 3 |    | {} | {6,3} |  | |||
| 3 [6] 3 | del3,3 2= 3 {6} 3 |    | 3 {} | {3,6} |  | Lo mismo que   | |
| 4 [8] 2 | del4,2 2= 4 {8} 2 |    | 4 {} | {4,4} |  | Lo mismo que    | |
| del2,4 2= 2 {8} 4 |    | {} | {4,4} |  | |||
| 4 [4] 4 | del4,4 2= 4 {4} 4 |    | 4 {} | {4,4} |  | Lo mismo que   | |
| 6 [6] 2 | del6,2 2= 6 {6} 2 |    | 6 {} | r{3,6} |  | Lo mismo que   | |
| del2,6 2= 2 {6} 6 |    | {} | {3,6} |  | |||
| 6 [4] 3 | del6,3 2= 6 {4} 3 |    | 6 {} | {6,3} |  | ||
| del3,6 2= 3 {4} 6 |    | 3 {} | {3,6} |  | |||
| 6 [3] 6 | del6,6 2= 6 {3} 6 |    | 6 {} | {3,6} |  | Lo mismo que   | |
Apeiroedros complejos regulares
Existen 22 apeiroedros complejos regulares de la forma p { a } q { b } r . 8 son autoduales ( p = r y a = b ), mientras que 14 existen como pares de politopos duales. Tres son completamente reales ( p = q = r =2).
Coxeter simboliza a 12 de ellos como δp , r
3o p {4} 2 {4} r es la forma regular del producto aperiótopo δp , r
2× δp , r
2o p { q } r × p { q } r , donde q se determina a partir de p y r .




 es lo mismo que
es lo mismo que

 , así como
, así como





 , para p , r = 2,3,4,6. También
, para p , r = 2,3,4,6. También



 =
=



 . [33]
. [33]
| Espacio | Grupo | Apeiroedro | Vértice | Borde | Rostro | Apeirogon de van Oss | Notas | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 [3] 2 [4] ∞ | ∞ {4} 2 {3} 2 | 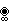     | ∞ {} | ∞ {4} 2 | Igual que ∞ {}× ∞ {}× ∞ {} o     Representación real {4,3,4} | |||||
| pág [4] 2 [4] r | p {4} 2 {4} r |      | pág. 2 | 2 pr | pag {} | r2 | pág {4} 2 | 2 { q } r | Lo mismo que       , p , r = 2,3,4,6 , p , r = 2,3,4,6 | |
| [4,4] | del2,2 3= {4,4} |      | 4 | 8 | {} | 4 | {4} | {∞} | Azulejo cuadrado real Igual que        o o       o o     | |
| 3 [4] 2 [4] 2 3 [ 4] 2 [ 4] 3 4 [4] 2 [4] 2 4 [4] 2 [4 ] 4 6 [4] 2 [4] 2 6 [4] 2 [4] 3 6 [4] 2 [4] 6 | 3 {4} 2 {4} 2 2 {4} 2 {4} 3 3 {4} 2 {4} 3 4 {4} 2 {4} 2 2 {4} 2 {4} 4 4 {4} 2 {4} 4 6 {4} 2 {4} 2 2 {4} 2 {4} 6 6 {4} 2 {4} 3 3 {4} 2 {4} 6 6 {4} 2 {4} 6 |                                                        | 9 4 9 16 4 16 36 4 36 9 36 | 12 12 18 16 16 32 24 24 36 36 72 | 3 {} {} 3 {} 4 {} { } 4 { } 6 {} {} 6 {} 3 {} 6 {} | 4 9 9 4 16 16 4 36 9 36 36 | 3 {4} 2 {4} 3 {4} 2 4 {4} 2 {4} 4 {4} 2 6 {4} 2 {4} 6 {4} 2 3 {4} 2 6 {4} 2 | p { q } r | Lo mismo que       o o       o o     Lo mismo que        Lo mismo que        Lo mismo que        o o       o o     Lo mismo que        Lo mismo que        Lo mismo que        o o       o o     Lo mismo que        Lo mismo que        Lo mismo que        Lo mismo que        | |
| Espacio | Grupo | Apeiroedro | Vértice | Borde | Rostro | Apeirogon de van Oss | Notas | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 [4] r [4] 2 | 2 {4} r {4} 2 |      | 2 | {} | 2 | pág {4} 2' | 2 {4} r | Lo mismo que     y y     , r=2,3,4,6 , r=2,3,4,6 | ||
| [4,4] | {4,4} |      | 2 | 4 | {} | 2 | {4} | {∞} | Lo mismo que     y y     | |
| 2 [4] 3 [4] 2 2 [4] 4 [4] 2 2 [4] 6 [4] 2 | 2 {4} 3 {4} 2 2 {4} 4 {4} 2 2 {4} 6 {4} 2 |                | 2 | 9 16 36 | {} | 2 | 2 {4} 3 2 {4} 4 2 {4} 6 | 2 { q } r | Lo mismo que     y y     Lo mismo que      y y     Lo mismo que      y y     [34] [34] | |
| Espacio | Grupo | Apeiroedro | Vértice | Borde | Rostro | Apeirogon de van Oss | Notas | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 [6] 2 [3] 2 = [6,3] | {3,6} |      | 1 | 3 | {} | 2 | {3} | {∞} | Azulejo triangular real | |
| {6,3} |      | 2 | 3 | {} | 1 | {6} | ninguno | Azulejos hexagonales reales | ||
| 3 [4] 3 [3] 3 | 3 {3} 3 {4} 3 |      | 1 | 8 | 3 {} | 3 | 3 {3} 3 | 3 {4} 6 | Lo mismo que    | |
| 3 {4} 3 {3} 3 |      | 3 | 8 | 3 {} | 1 | 3 {4} 3 | 3 {12} 2 | |||
| 4 [3] 4 [3] 4 | 4 {3} 4 {3} 4 |      | 1 | 6 | 4 {} | 1 | 4 {3} 4 | 4 {4} 4 | Auto-dual, lo mismo que     | |
| 4 [3] 4 [4] 2 | 4 {3} 4 {4} 2 |      | 1 | 12 | 4 {} | 3 | 4 {3} 4 | 2 {8} 4 | Lo mismo que     | |
| 2 {4} 4 {3} 4 |      | 3 | 12 | {} | 1 | 2 {4} 4 | 4 {4} 4 | |||
3-apeirotopos complejos regulares
Hay 16 aperiótopos complejos regulares en . Coxeter expresa 12 de ellos mediante δp , r
3donde q está restringido a satisfacer q = 2/(1 – ( p + r )/ pr ) . Estos también pueden descomponerse como aperiótopos de producto:





 =
=









 El primer caso es el panal cúbico .
El primer caso es el panal cúbico .
| Espacio | Grupo | 3-apeirotopo | Vértice | Borde | Rostro | Celúla | Apeirogon de van Oss | Notas |
|---|---|---|---|---|---|---|---|---|
| pág. [4] 2 [3] 2 [4] r | delp , r 3= p {4} 2 {3} 2 {4} r        | pag {} | pág {4} 2 | pág. {4} 2 {3} 2 | p { q } r | Lo mismo que           | ||
| 2 [4] 2 [3] 2 [4] 2 =[4,3,4] | del2,2 3= 2 {4} 2 {3} 2 {4} 2        | {} | {4} | {4,3} | Panal cúbico Igual que            o o           o o       | |||
| 3 [4] 2 [3] 2 [4] 2 | del3,2 3= 3 {4} 2 {3} 2 {4} 2        | 3 {} | 3 {4} 2 | 3 {4} 2 {3} 2 | Lo mismo que           o o           o o       | |||
| del2,3 3= 2 {4} 2 {3} 2 {4} 3        | {} | {4} | {4,3} | Lo mismo que           | ||||
| 3 [4] 2 [3] 2 [4] 3 | del3,3 3= 3 {4} 2 {3} 2 {4} 3        | 3 {} | 3 {4} 2 | 3 {4} 2 {3} 2 | Lo mismo que           | |||
| 4 [4] 2 [3] 2 [4] 2 | del4,2 3 = 4{4}2{3}2{4}2        | 4{} | 4{4}2 | 4{4}2{3}2 | Same as            or or            or or        | |||
| δ2,4 3 = 2{4}2{3}2{4}4        | {} | {4} | {4,3} | Same as            | ||||
| 4[4]2[3]2[4]4 | δ4,4 3 = 4{4}2{3}2{4}4        | 4{} | 4{4}2 | 4{4}2{3}2 | Same as            | |||
| 6[4]2[3]2[4]2 | δ6,2 3 = 6{4}2{3}2{4}2        | 6{} | 6{4}2 | 6{4}2{3}2 | Same as            or or            or or        | |||
| δ2,6 3 = 2{4}2{3}2{4}6        | {} | {4} | {4,3} | Same as            | ||||
| 6[4]2[3]2[4]3 | δ6,3 3 = 6{4}2{3}2{4}3        | 6{} | 6{4}2 | 6{4}2{3}2 | Same as            | |||
| δ3,6 3 = 3{4}2{3}2{4}6        | 3{} | 3{4}2 | 3{4}2{3}2 | Same as            | ||||
| 6[4]2[3]2[4]6 | δ6,6 3 = 6{4}2{3}2{4}6        | 6{} | 6{4}2 | 6{4}2{3}2 | Same as            |
| Space | Group | 3-apeirotope | Vertex | Edge | Face | Cell | van Oss apeirogon | Notes |
|---|---|---|---|---|---|---|---|---|
| 2[4]3[3]3[3]3 | 3{3}3{3}3{4}2       | 1 | 24 3{} | 27 3{3}3 | 2 3{3}3{3}3 | 3{4}6 | Same as       | |
2{4}3{3}3{3}3       | 2 | 27 {} | 24 2{4}3 | 1 2{4}3{3}3 | 2{12}3 | |||
| 2[3]2[4]3[3]3 | 2{3}2{4}3{3}3       | 1 | 27 {} | 72 2{3}2 | 8 2{3}2{4}3 | 2{6}6 | ||
3{3}3{4}2{3}2       | 8 | 72 3{} | 27 3{3}3 | 1 3{3}3{4}2 | 3{6}3 | Same as       or or        |
Regular complex 4-apeirotopes
There are 15 regular complex apeirotopes in . Coxeter expresses 12 of them by δp,r
4 where q is constrained to satisfy q = 2/(1 – (p + r)/pr). These can also be decomposed as product apeirotopes: 







 =
= 













 . The first case is the tesseractic honeycomb. The 16-cell honeycomb and 24-cell honeycomb are real solutions. The last solution is generated has Witting polytope elements.
. The first case is the tesseractic honeycomb. The 16-cell honeycomb and 24-cell honeycomb are real solutions. The last solution is generated has Witting polytope elements.
| Space | Group | 4-apeirotope | Vertex | Edge | Face | Cell | 4-face | van Oss apeirogon | Notes |
|---|---|---|---|---|---|---|---|---|---|
| p[4]2[3]2[3]2[4]r | δp,r 4 = p{4}2{3}2{3}2{4}r          | p{} | p{4}2 | p{4}2{3}2 | p{4}2{3}2{3}2 | p{q}r | Same as                | ||
| 2[4]2[3]2[3]2[4]2 | δ2,2 4 = {4,3,3,3}          | {} | {4} | {4,3} | {4,3,3} | {∞} | Tesseractic honeycomb Same as                | ||
| 2[3]2[4]2[3]2[3]2 =[3,4,3,3] | {3,3,4,3}          | 1 | 12 {} | 32 {3} | 24 {3,3} | 3 {3,3,4} | Real 16-cell honeycomb Same as      | ||
{3,4,3,3}         | 3 | 24 {} | 32 {3} | 12 {3,4} | 1 {3,4,3} | Real 24-cell honeycomb Same as      or or          | |||
| 3[3]3[3]3[3]3[3]3 | 3{3}3{3}3{3}3{3}3         | 1 | 80 3{} | 270 3{3}3 | 80 3{3}3{3}3 | 1 3{3}3{3}3{3}3 | 3{4}6 | representation 521 |
Regular complex 5-apeirotopes and higher
There are only 12 regular complex apeirotopes in or higher,[35] expressed δp,r
n where q is constrained to satisfy q = 2/(1 – (p + r)/pr). These can also be decomposed a product of n apeirogons: 



 ...
... 




 =
= 





 ...
... 





 . The first case is the real hypercube honeycomb.
. The first case is the real hypercube honeycomb.
| Space | Group | 5-apeirotopes | Vertices | Edge | Face | Cell | 4-face | 5-face | van Oss apeirogon | Notes |
|---|---|---|---|---|---|---|---|---|---|---|
| p[4]2[3]2[3]2[3]2[4]r | δp,r 5 = p{4}2{3}2{3}2{3}2{4}r            | p{} | p{4}2 | p{4}2{3}2 | p{4}2{3}2{3}2 | p{4}2{3}2{3}2{3}2 | p{q}r | Same as                    | ||
| 2[4]2[3]2[3]2[3]2[4]2 =[4,3,3,3,4] | δ2,2 5 = {4,3,3,3,4}            | {} | {4} | {4,3} | {4,3,3} | {4,3,3,3} | {∞} | 5-cubic honeycomb Same as                    |
van Oss polygon

A van Oss polygon is a regular polygon in the plane (real plane , or unitary plane ) in which both an edge and the centroid of a regular polytope lie, and formed of elements of the polytope. Not all regular polytopes have Van Oss polygons.
For example, the van Oss polygons of a real octahedron are the three squares whose planes pass through its center. In contrast a cube does not have a van Oss polygon because the edge-to-center plane cuts diagonally across two square faces and the two edges of the cube which lie in the plane do not form a polygon.
Infinite honeycombs also have van Oss apeirogons. For example, the real square tiling and triangular tiling have apeirogons {∞} van Oss apeirogons.[36]
If it exists, the van Oss polygon of regular complex polytope of the form p{q}r{s}t... has p-edges.
Non-regular complex polytopes
Product complex polytopes
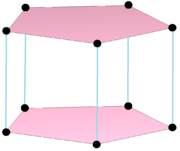 Complex product polygon    or {}×5{} has 10 vertices connected by 5 2-edges and 2 5-edges, with its real representation as a 3-dimensional pentagonal prism. or {}×5{} has 10 vertices connected by 5 2-edges and 2 5-edges, with its real representation as a 3-dimensional pentagonal prism. | 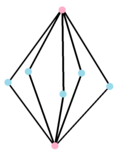 The dual polygon,{}+5{} has 7 vertices centered on the edges of the original, connected by 10 edges. Its real representation is a pentagonal bipyramid. |
Some complex polytopes can be represented as Cartesian products. These product polytopes are not strictly regular since they'll have more than one facet type, but some can represent lower symmetry of regular forms if all the orthogonal polytopes are identical. For example, the product p{}×p{} or 

 of two 1-dimensional polytopes is the same as the regular p{4}2 or
of two 1-dimensional polytopes is the same as the regular p{4}2 or 

 . More general products, like p{}×q{} have real representations as the 4-dimensional p-q duoprisms. The dual of a product polytope can be written as a sum p{}+q{} and have real representations as the 4-dimensional p-q duopyramid. The p{}+p{} can have its symmetry doubled as a regular complex polytope 2{4}p or
. More general products, like p{}×q{} have real representations as the 4-dimensional p-q duoprisms. The dual of a product polytope can be written as a sum p{}+q{} and have real representations as the 4-dimensional p-q duopyramid. The p{}+p{} can have its symmetry doubled as a regular complex polytope 2{4}p or 

 .
.
Similarly, a complex polyhedron can be constructed as a triple product: p{}×p{}×p{} or 



 is the same as the regular generalized cube, p{4}2{3}2 or
is the same as the regular generalized cube, p{4}2{3}2 or 



 , as well as product p{4}2×p{} or
, as well as product p{4}2×p{} or 



 .[37]
.[37]
Quasiregular polygons
A quasiregular polygon is a truncation of a regular polygon. A quasiregular polygon 

 contains alternate edges of the regular polygons
contains alternate edges of the regular polygons 

 and
and 

 . The quasiregular polygon has p vertices on the p-edges of the regular form.
. The quasiregular polygon has p vertices on the p-edges of the regular form.
Quasiregular apeirogons
There are 7 quasiregular complex apeirogons which alternate edges of a regular apeirogon and its regular dual. The vertex arrangements of these apeirogon have real representations with the regular and uniform tilings of the Euclidean plane. The last column for the 6{3}6 apeirogon is not only self-dual, but the dual coincides with itself with overlapping hexagonal edges, thus their quasiregular form also has overlapping hexagonal edges, so it can't be drawn with two alternating colors like the others. The symmetry of the self-dual families can be doubled, so creating an identical geometry as the regular forms: 

 =
= 



| p[q]r | 4[8]2 | 4[4]4 | 6[6]2 | 6[4]3 | 3[12]2 | 3[6]3 | 6[3]6 |
|---|---|---|---|---|---|---|---|
Regular   or p{q}r or p{q}r |     |     |     |     |     |     |     |
Quasiregular   |     |     = =    |     |     | 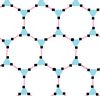    |     = =    |     = =    |
Regular dual   or r{q}p or r{q}p |     |     |     |     |     |     | 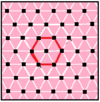    |
Quasiregular polyhedra





 , to its rectified limit, showing outlined-green triangles faces at the start, and blue 2{4}3,
, to its rectified limit, showing outlined-green triangles faces at the start, and blue 2{4}3, 

 , vertex figures expanding as new faces.
, vertex figures expanding as new faces.Like real polytopes, a complex quasiregular polyhedron can be constructed as a rectification (a complete truncation) of a regular polyhedron. Vertices are created mid-edge of the regular polyhedron and faces of the regular polyhedron and its dual are positioned alternating across common edges.
For example, a p-generalized cube, 



 , has p3 vertices, 3p2 edges, and 3p p-generalized square faces, while the p-generalized octahedron,
, has p3 vertices, 3p2 edges, and 3p p-generalized square faces, while the p-generalized octahedron, 



 , has 3p vertices, 3p2 edges and p3 triangular faces. The middle quasiregular form p-generalized cuboctahedron,
, has 3p vertices, 3p2 edges and p3 triangular faces. The middle quasiregular form p-generalized cuboctahedron, 



 , has 3p2 vertices, 3p3 edges, and 3p+p3 faces.
, has 3p2 vertices, 3p3 edges, and 3p+p3 faces.
Also the rectification of the Hessian polyhedron 



 , is
, is 



 , a quasiregular form sharing the geometry of the regular complex polyhedron
, a quasiregular form sharing the geometry of the regular complex polyhedron 



 .
.
| Generalized cube/octahedra | Hessian polyhedron | |||||
|---|---|---|---|---|---|---|
| p=2 (real) | p=3 | p=4 | p=5 | p=6 | ||
| Generalized cubes      (regular) |  Cube      , 8 vertices, 12 2-edges, and 6 faces. , 8 vertices, 12 2-edges, and 6 faces. |       , 27 vertices, 27 3-edges, and 9 faces, with one , 27 vertices, 27 3-edges, and 9 faces, with one    face blue and red face blue and red |       , 64 vertices, 48 4-edges, and 12 faces. , 64 vertices, 48 4-edges, and 12 faces. |       , 125 vertices, 75 5-edges, and 15 faces. , 125 vertices, 75 5-edges, and 15 faces. |       , 216 vertices, 108 6-edges, and 18 faces. , 216 vertices, 108 6-edges, and 18 faces. |       , 27 vertices, 72 6-edges, and 27 faces. , 27 vertices, 72 6-edges, and 27 faces. |
| Generalized cuboctahedra      (quasiregular) | 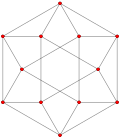 Cuboctahedron      , 12 vertices, 24 2-edges, and 6+8 faces. , 12 vertices, 24 2-edges, and 6+8 faces. |       , 27 vertices, 81 2-edges, and 9+27 faces, with one , 27 vertices, 81 2-edges, and 9+27 faces, with one    face blue face blue |       , 48 vertices, 192 2-edges, and 12+64 faces, with one , 48 vertices, 192 2-edges, and 12+64 faces, with one    face blue face blue |       , 75 vertices, 375 2-edges, and 15+125 faces. , 75 vertices, 375 2-edges, and 15+125 faces. |       , 108 vertices, 648 2-edges, and 18+216 faces. , 108 vertices, 648 2-edges, and 18+216 faces. | 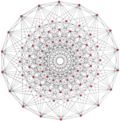      = =      , 72 vertices, 216 3-edges, and 54 faces. , 72 vertices, 216 3-edges, and 54 faces. |
| Generalized octahedra      (regular) |  Octahedron      , 6 vertices, 12 2-edges, and 8 {3} faces. , 6 vertices, 12 2-edges, and 8 {3} faces. | 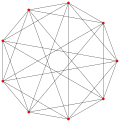      , 9 vertices, 27 2-edges, and 27 {3} faces. , 9 vertices, 27 2-edges, and 27 {3} faces. |       , 12 vertices, 48 2-edges, and 64 {3} faces. , 12 vertices, 48 2-edges, and 64 {3} faces. |       , 15 vertices, 75 2-edges, and 125 {3} faces. , 15 vertices, 75 2-edges, and 125 {3} faces. |       , 18 vertices, 108 2-edges, and 216 {3} faces. , 18 vertices, 108 2-edges, and 216 {3} faces. |       , 27 vertices, 72 6-edges, and 27 faces. , 27 vertices, 72 6-edges, and 27 faces. |
Other complex polytopes with unitary reflections of period two
Other nonregular complex polytopes can be constructed within unitary reflection groups that don't make linear Coxeter graphs. In Coxeter diagrams with loops Coxeter marks a special period interior, like 

 or symbol (11 1 1)3, and group [1 1 1]3.[38][39] These complex polytopes have not been systematically explored beyond a few cases.
or symbol (11 1 1)3, and group [1 1 1]3.[38][39] These complex polytopes have not been systematically explored beyond a few cases.
The group 
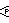
 is defined by 3 unitary reflections, R1, R2, R3, all order 2: R12 = R12 = R32 = (R1R2)3 = (R2R3)3 = (R3R1)3 = (R1R2R3R1)p = 1. The period p can be seen as a double rotation in real .
is defined by 3 unitary reflections, R1, R2, R3, all order 2: R12 = R12 = R32 = (R1R2)3 = (R2R3)3 = (R3R1)3 = (R1R2R3R1)p = 1. The period p can be seen as a double rotation in real .
As with all Wythoff constructions, polytopes generated by reflections, the number of vertices of a single-ringed Coxeter diagram polytope is equal to the order of the group divided by the order of the subgroup where the ringed node is removed. For example, a real cube has Coxeter diagram 



 , with octahedral symmetry
, with octahedral symmetry 



 order 48, and subgroup dihedral symmetry
order 48, and subgroup dihedral symmetry 

 order 6, so the number of vertices of a cube is 48/6=8. Facets are constructed by removing one node furthest from the ringed node, for example
order 6, so the number of vertices of a cube is 48/6=8. Facets are constructed by removing one node furthest from the ringed node, for example 

 for the cube. Vertex figures are generated by removing a ringed node and ringing one or more connected nodes, and
for the cube. Vertex figures are generated by removing a ringed node and ringing one or more connected nodes, and 

 for the cube.
for the cube.
Coxeter represents these groups by the following symbols. Some groups have the same order, but a different structure, defining the same vertex arrangement in complex polytopes, but different edges and higher elements, like 
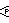
 and
and 


 with p≠3.[40]
with p≠3.[40]
| Coxeter diagram | Order | Symbol or Position in Table VII of Shephard and Todd (1954) |
|---|---|---|
  , ( , (   and and     ), ),       , ,         ... ... | pn − 1 n!, p ≥ 3 | G(p, p, n), [p], [1 1 1]p, [1 1 (n−2)p]3 |
     , ,        | 72·6!, 108·9! | Nos. 33, 34, [1 2 2]3, [1 2 3]3 |
    , ( , (    and and     ), ( ), (     and and      ) ) | 14·4!, 3·6!, 64·5! | Nos. 24, 27, 29 |
Coxeter calls some of these complex polyhedra almost regular because they have regular facets and vertex figures. The first is a lower symmetry form of the generalized cross-polytope in . The second is a fractional generalized cube, reducing p-edges into single vertices leaving ordinary 2-edges. Three of them are related to the finite regular skew polyhedron in .
| Space | Group | Order | Coxeter symbols | Vertices | Edges | Faces | Vertex figure | Notes |
|---|---|---|---|---|---|---|---|---|
[1 1 1p]3    p=2,3,4... | 6p2 | (1 1 11p)3    | 3p | 3p2 | {3} | {2p} | Shephard symbol (1 1; 11)p same as βp 3 =      | |
(11 1 1p)3    | p2 | {3} | {6} | Shephard symbol (11 1; 1)p 1/p γp 3 | ||||
[1 1 12]3   | 24 | (1 1 112)3   | 6 | 12 | 8 {3} | {4} | Same as β2 3 =      = real octahedron = real octahedron | |
(11 1 12)3   | 4 | 6 | 4 {3} | {3} | 1/2 γ2 3 =      = α3 = real tetrahedron = α3 = real tetrahedron | |||
[1 1 1]3   | 54 | (1 1 11)3   | 9 | 27 | {3} | {6} | Shephard symbol (1 1; 11)3 same as β3 3 =      | |
(11 1 1)3   | 9 | 27 | {3} | {6} | Shephard symbol (11 1; 1)3 1/3 γ3 3 = β3 3 | |||
[1 1 14]3    | 96 | (1 1 114)3    | 12 | 48 | {3} | {8} | Shephard symbol (1 1; 11)4 same as β4 3 =      | |
(11 1 14)3    | 16 | {3} | {6} | Shephard symbol (11 1; 1)4 1/4 γ4 3 | ||||
[1 1 15]3    | 150 | (1 1 115)3    | 15 | 75 | {3} | {10} | Shephard symbol (1 1; 11)5 same as β5 3 =      | |
(11 1 15)3    | 25 | {3} | {6} | Shephard symbol (11 1; 1)5 1/5 γ5 3 | ||||
[1 1 16]3    | 216 | (1 1 116)3    | 18 | 216 | {3} | {12} | Shephard symbol (1 1; 11)6 same as β6 3 =      | |
(11 1 16)3    | 36 | {3} | {6} | Shephard symbol (11 1; 1)6 1/6 γ6 3 | ||||
[1 1 14]4 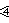   | 336 | (1 1 114)4 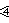   | 42 | 168 | 112 {3} | {8} | representation {3,8|,4} = {3,8}8 | |
(11 1 14)4 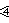   | 56 | {3} | {6} | |||||
[1 1 15]4    | 2160 | (1 1 115)4    | 216 | 1080 | 720 {3} | {10} | representation {3,10|,4} = {3,10}8 | |
(11 1 15)4    | 360 | {3} | {6} | |||||
[1 1 14]5    | (1 1 114)5    | 270 | 1080 | 720 {3} | {8} | representation {3,8|,5} = {3,8}10 | ||
(11 1 14)5    | 360 | {3} | {6} |
Coxeter defines other groups with anti-unitary constructions, for example these three. The first was discovered and drawn by Peter McMullen in 1966.[42]
| Space | Group | Order | Coxeter symbols | Vertices | Edges | Faces | Vertex figure | Notes |
|---|---|---|---|---|---|---|---|---|
[1 14 14](3)   | 336 | (11 14 14)(3)   | 56 | 168 | 84 {4} | {6} | representation {4,6|,3} = {4,6}6 | |
[15 14 14](3)    | 2160 | (115 14 14)(3) 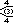   | 216 | 1080 | 540 {4} | {10} | representation {4,10|,3} = {4,10}6 | |
[14 15 15](3) 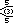   | (114 15 15)(3) 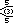   | 270 | 1080 | 432 {5} | {8} | representation {5,8|,3} = {5,8}6 |
| Space | Group | Order | Coxeter symbols | Vertices | Other elements | Cells | Vertex figure | Notes |
|---|---|---|---|---|---|---|---|---|
[1 1 2p]3      p=2,3,4... | 24p3 | (1 1 22p)3      | 4p |      |     | Shephard (22 1; 1)p same as βp 4 =        | ||
(11 1 2p )3    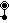  | p3 |        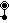  |      | Shephard (2 1; 11)p 1/p γp 4 | ||||
| [1 1 22]3 =[31,1,1]      | 192 | (1 1 222)3     | 8 | 24 edges 32 faces | 16      |    | β2 4 =        , real 16-cell , real 16-cell | |
(11 1 22 )3     | 1/2 γ2 4 =        = β2 = β24, real 16-cell | |||||||
[1 1 2]3     | 648 | (1 1 22)3     | 12 |      |    | Shephard (22 1; 1)3 same as β3 4 =        | ||
(11 1 23)3    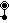 | 27 |        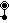 |      | Shephard (2 1; 11)3 1/3 γ3 4 | ||||
[1 1 24]3      | 1536 | (1 1 224)3      | 16 |      |     | Shephard (22 1; 1)4 same as β4 4 =        | ||
(11 1 24 )3      | 64 |          |      | Shephard (2 1; 11)4 1/4 γ4 4 | ||||
[14 1 2]3     | 7680 | (22 14 1)3     | 80 |      |    | Shephard (22 1; 1)4 | ||
(114 1 2)3     | 160 |         |      | Shephard (2 1; 11)4 | ||||
(11 14 2)3     | 320 |         |      | Shephard (2 11; 1)4 | ||||
[1 1 2]4   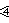  | (1 1 22)4   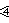  | 80 | 640 edges 1280 triangles | 640      |  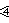  | |||
(11 1 2)4     | 320 |         |      |
| Space | Group | Order | Coxeter symbols | Vertices | Edges | Facets | Vertex figure | Notes |
|---|---|---|---|---|---|---|---|---|
[1 1 3p]3        p=2,3,4... | 120p4 | (1 1 33p)3        | 5p |        |       | Shephard (33 1; 1)p same as βp 5 =          | ||
(11 1 3p)3        | p4 |              |        | Shephard (3 1; 11)p 1/p γp 5 | ||||
[2 2 1]3     | 51840 | (2 1 22)3     | 80 |         |      | Shephard (2 1; 22)3 | ||
(2 11 2)3     | 432 |      |    | Shephard (2 11; 2)3 |
| Space | Group | Order | Coxeter symbols | Vertices | Edges | Facets | Vertex figure | Notes |
|---|---|---|---|---|---|---|---|---|
[1 1 4p]3          p=2,3,4... | 720p5 | (1 1 44p)3          | 6p |          |         | Shephard (44 1; 1)p same as βp 6 =            | ||
(11 1 4p)3          | p5 |                  |        | Shephard (4 1; 11)p 1/p γp 6 | ||||
[1 2 3]3       | 39191040 | (2 1 33)3       | 756 |             |      | Shephard (2 1; 33)3 | ||
(22 1 3)3       | 4032 |           |        | Shephard (22 1; 3)3 | ||||
(2 11 3)3       | 54432 |             |      | Shephard (2 11; 3)3 |
Visualizations
- (1 1 114)4,



 has 42 vertices, 168 edges and 112 triangular faces, seen in this 14-gonal projection.
has 42 vertices, 168 edges and 112 triangular faces, seen in this 14-gonal projection. - (14 14 11)(3),


 has 56 vertices, 168 edges and 84 square faces, seen in this 14-gonal projection.
has 56 vertices, 168 edges and 84 square faces, seen in this 14-gonal projection. - (1 1 22)4,




 has 80 vertices, 640 edges, 1280 triangular faces and 640 tetrahedral cells, seen in this 20-gonal projection.[43]
has 80 vertices, 640 edges, 1280 triangular faces and 640 tetrahedral cells, seen in this 20-gonal projection.[43]
See also
Notes
- ^ Peter Orlik, Victor Reiner, Anne V. Shepler. The sign representation for Shephard groups. Mathematische Annalen. March 2002, Volume 322, Issue 3, pp 477–492. DOI:10.1007/s002080200001 [1]
- ^ Coxeter, Regular Complex Polytopes, p. 115
- ^ Coxeter, Regular Complex Polytopes, 11.3 Petrie Polygon, a simple h-gon formed by the orbit of the flag (O0,O0O1) for the product of the two generating reflections of any nonstarry regular complex polygon, p1{q}p2.
- ^ Complex Regular Polytopes,11.1 Regular complex polygons p.103
- ^ Shephard, 1952; "It is from considerations such as these that we derive the notion of the interior of a polytope, and it will be seen that in unitary space where the numbers cannot be so ordered such a concept of interior is impossible. [Para break] Hence ... we have to consider unitary polytopes as configurations."
- ^ Coxeter, Regular Complex polytopes, p. 96
- ^ Coxeter, Regular Complex Polytopes, p. xiv
- ^ Coxeter, Complex Regular Polytopes, p. 177, Table III
- ^ Lehrer & Taylor 2009, p. 87
- ^ Coxeter, Regular Complex Polytopes, Table IV. The regular polygons. pp. 178–179
- ^ Complex Polytopes, 8.9 The Two-Dimensional Case, p. 88
- ^ Regular Complex Polytopes, Coxeter, pp. 177-179
- ^ a b Coxeter, Regular Complex Polytopes, p. 108
- ^ Coxeter, Regular Complex Polytopes, p. 109
- ^ Coxeter, Regular Complex Polytopes, p. 111
- ^ Coxeter, Regular Complex Polytopes, p. 30 diagram and p. 47 indices for 8 3-edges
- ^ a b Coxeter, Regular Complex Polytopes, p. 110
- ^ Coxeter, Regular Complex Polytopes, p. 48
- ^ Coxeter, Regular Complex Polytopes, p. 49
- ^ Coxeter, Regular Complex Polytopes, pp. 116–140.
- ^ a b Coxeter, Regular Complex Polytopes, pp. 118–119.
- ^ Complex Regular Polytopes, p.29
- ^ a b Coxeter, Regular Complex Polytopes, Table V. The nonstarry regular polyhedra and 4-polytopes. p. 180.
- ^ Coxeter, Kaleidoscopes — Selected Writings of H.S.M. Coxeter, Paper 25 Surprising relationships among unitary reflection groups, p. 431.
- ^ a b Coxeter, Regular Complex Polytopes, p. 131
- ^ Coxeter, Regular Complex Polytopes, p. 126
- ^ Coxeter, Regular Complex Polytopes, p. 125
- ^ Coxeter, Regular Complex Polytopes, Table VI. The regular honeycombs. p. 180.
- ^ Complex regular polytope, p.174
- ^ Coxeter, Regular Complex Polytopes, Table VI. The regular honeycombs. p. 111, 136.
- ^ Coxeter, Regular Complex Polytopes, Table IV. The regular polygons. pp. 178–179
- ^ Coxeter, Politopos complejos regulares, 11.6 Apeirogons, págs. 111-112
- ^ Coxeter, Politopos regulares complejos, p.140
- ^ Coxeter, Politopos complejos regulares, págs. 139-140
- ^ Politopos regulares complejos, p.146
- ^ Politopos regulares complejos, p.141
- ^ Coxeter, Politopos complejos regulares, págs. 118-119, 138.
- ^ Coxeter, Politopos complejos regulares, Capítulo 14, Politopos casi regulares , págs. 156-174.
- ^ Coxeter, Grupos generados por reflexiones unitarias del período dos , 1956
- ^ Coxeter , Grupos finitos generados por reflexiones unitarias , 1966, 4. La notación gráfica , Tabla de grupos n -dimensionales generados por n reflexiones unitarias. pp. 422-423
- ^ abcde Coxeter, Grupos generados por reflexiones unitarias del período dos (1956), Tabla III: Algunos politopos complejos, p.413
- ^ Coxeter, Complex Regular Polytopes, (1991), 14.6 Dos poliedros de McMullen con 84 caras cuadradas, pp.166-171
- ^ Coxeter, Politopos regulares complejos, págs. 172-173
Referencias
- Coxeter, HSM y Moser, WOJ; Generadores y relaciones para grupos discretos (1965), esp pp 67–80.
- Coxeter, HSM (1991), Politopos complejos regulares , Cambridge University Press, ISBN 0-521-39490-2
- Coxeter, HSM y Shephard, GC; Retratos de una familia de politopos complejos, Leonardo Vol 25, No 3/4, (1992), pp 239–244,
- Shephard, GC; Politopos complejos regulares , Proc. London Math. Soc. Serie 3, vol. 2, (1952), págs. 82–97.
- GC Shephard , JA Todd, Grupos de reflexión unitaria finitos , Revista canadiense de matemáticas. 6(1954), 274-304, doi :10.4153/CJM-1954-028-3
- Gustav I. Lehrer y Donald E. Taylor, Unitary Reflection Groups , Cambridge University Press, 2009
Lectura adicional
- F. Arthur Sherk, Peter McMullen, Anthony C. Thompson y Asia Ivić Weiss, editores: Kaleidoscopes — Selected Writings of HSM Coxeter. , Documento 25, Grupos finitos generados por reflexiones unitarias , pág. 415-425, John Wiley, 1995, ISBN 0-471-01003-0
- McMullen, Peter ; Schulte, Egon (diciembre de 2002), Abstract Regular Polytopes (1.ª ed.), Cambridge University Press , ISBN 0-521-81496-0Capítulo 9 Grupos unitarios y formas hermíticas , págs. 289–298








![{\displaystyle \left[{\begin{smallmatrix}e^{2\pi i/p}&0\\(e^{2\pi i/p}-1)k&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d128407ddca614c4bed7308acba9bd274b704c5c)
![{\displaystyle \left[{\begin{smallmatrix}1&(e^{2\pi i/r}-1)k\\0&e^{2\pi i/r}\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de7bd24e7be60162da1fa1566fea5571820d3e82)

![{\displaystyle \left[{\begin{smallmatrix}e^{2\pi i/p}&0\\0&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/922057855ba2380fdbf36b0e91f0afe08b867bcb)
![{\displaystyle \left[{\begin{smallmatrix}1&0\\0&e^{2\pi i/q}\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6991a4012a94e23b3475fd268007ca2aeba4bcbe)
![{\displaystyle \left[{\begin{smallmatrix}0&1\\1&0\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9694a3311550c844e792232f8c8742c6f3c9d32f)
![{\displaystyle \left[{\begin{smallmatrix}{\frac {-1+{\sqrt {3}}i}{2}}&0\\{\frac {-3+{\sqrt {3}}i}{2}}&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef7975113174eb40a8488733bebb8fb4d1bd293)
![{\displaystyle \left[{\begin{smallmatrix}1&{\frac {-3+{\sqrt {3}}i}{2}}\\0&{\frac {-1+{\sqrt {3}}i}{2}}\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1081ee946ee626dd6ae6d776581d567006cd16fb)
![{\displaystyle \left[{\begin{smallmatrix}i&0\\0&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4087d1ec8773364a46947bc9f58bf721a413846c)
![{\displaystyle \left[{\begin{smallmatrix}1&0\\0&i\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3736413b59866ae2edd640f7bb77f7b8bdd6a9d)
![{\displaystyle \left[{\begin{smallmatrix}1&-2\\0&-1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de49a4aea18b37177252a0f6c2a3707c14b9b910)


![2{4}3, , con 6 vértices y 9 aristas[13]](http://upload.wikimedia.org/wikipedia/commons/thumb/7/70/Complex_polygon_2-4-3-bipartite_graph.png/120px-Complex_polygon_2-4-3-bipartite_graph.png)

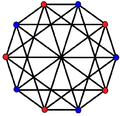
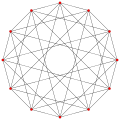




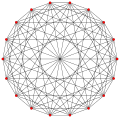



![3{4}2, o , con 9 vértices y 6 aristas triangulares de 3 puntos[13]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/dc/3-generalized-2-cube_skew.svg/120px-3-generalized-2-cube_skew.svg.png)
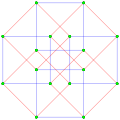

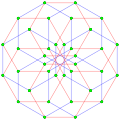




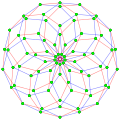



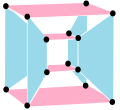

![3{6}2, o , con 24 vértices en negro y 16 aristas de 3 colores en 2 conjuntos de aristas de 3 colores en rojo y azul[14]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/36/Complex_polygon_3-6-2.png/120px-Complex_polygon_3-6-2.png)
![3{8}2, o , con 72 vértices en negro y 48 aristas de 3 colores en 2 conjuntos de aristas de 3 colores en rojo y azul[15]](http://upload.wikimedia.org/wikipedia/commons/thumb/0/00/Complex_polygon_3-8-2.png/120px-Complex_polygon_3-8-2.png)
![3{3}3, o , con 8 vértices en negro y 8 aristas de 3 colores en 2 conjuntos de aristas de 3 en rojo y azul[16]](http://upload.wikimedia.org/wikipedia/commons/thumb/e/ef/Complex_polygon_3-3-3.png/120px-Complex_polygon_3-3-3.png)
![3{4}3, o , con 24 vértices y 24 aristas de 3 lados que se muestran en 3 conjuntos de colores, un conjunto lleno[17]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/de/Complex_polygon_3-4-3-fill1.png/120px-Complex_polygon_3-4-3-fill1.png)
![4{3}4, o , con 24 vértices y 24 aristas de 4 lados que se muestran en 4 conjuntos de colores[17]](http://upload.wikimedia.org/wikipedia/commons/thumb/4/46/Complex_polygon_4-3-4.png/119px-Complex_polygon_4-3-4.png)
![3{5}3, o , con 120 vértices y 120 3 aristas[18]](http://upload.wikimedia.org/wikipedia/commons/thumb/2/20/Complex_polygon_3-5-3.png/120px-Complex_polygon_3-5-3.png)
![5{3}5, o , con 120 vértices y 120 aristas de 5[19]](http://upload.wikimedia.org/wikipedia/commons/thumb/b/b9/Complex_polygon_5-3-5.png/119px-Complex_polygon_5-3-5.png)



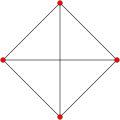
![3{3}3{3}3, o , tiene 27 vértices, 72 aristas de 3 lados y 27 caras, con una cara resaltada en azul.[25]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/df/Complex_polyhedron_3-3-3-3-3-one-blue-face.png/120px-Complex_polyhedron_3-3-3-3-3-one-blue-face.png)
![2{4}3{3}3, tiene 54 vértices, 216 aristas simples y 72 caras, con una cara resaltada en azul.[26]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1d/Complex_polyhedron_2-4-3-3-3_blue-edge.png/120px-Complex_polyhedron_2-4-3-3-3_blue-edge.png)
![3{3}3{4}2, o , tiene 72 vértices, 216 3 aristas y 54 vértices, con una cara resaltada en azul.[27]](http://upload.wikimedia.org/wikipedia/commons/thumb/8/86/Complex_polyhedron_3-3-3-4-2-one-blue-face.png/118px-Complex_polyhedron_3-3-3-4-2-one-blue-face.png)




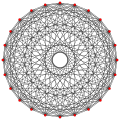




![3{4}2{3}2, o tiene 27 vértices, 27 aristas de 3 lados y 9 caras[25]](http://upload.wikimedia.org/wikipedia/commons/thumb/8/8d/3-generalized-3-cube.svg/118px-3-generalized-3-cube.svg.png)













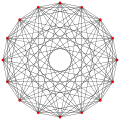
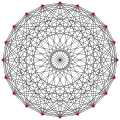






































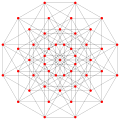








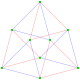
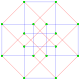
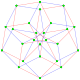
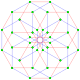
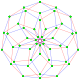

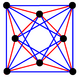

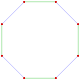
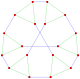
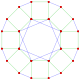

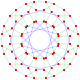



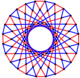
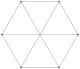
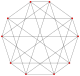


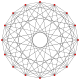


![(1 1 22)4, tiene 80 vértices, 640 aristas, 1280 caras triangulares y 640 celdas tetraédricas, que se ven en esta proyección de 20 gonales.[43]](http://upload.wikimedia.org/wikipedia/commons/thumb/e/ec/Complex_4-polytope_almost_regular_80_vertices.png/120px-Complex_4-polytope_almost_regular_80_vertices.png)
